Fact: Rational expressions have their own arithmetic (addition, subtraction, multiplication, and division).
Now that we know how to do arithmetic with rational expressions, we may now solve equations involving rational expressions.
Two Warm-Up Examples
$\frac{4}{\theta - 5}=\frac{2}{\theta + 3}$
$\frac{1}{h + 3}-5=\frac{1}{h + 3}$
Solving Equations with Rational Expression
Process: To solve an equation with rational expressions:
1) Multiply every term by something which cancels all the denominators.
2) Solve the resulting fraction-less equation.
3) Check for extraneous (fake) solutions.
Examples
$\frac{ a}{a^2+4 a - 32}-\frac{ a}{a^2 +13 a + 40}=\frac{3 a}{a^2+1 a - 20}$ (two bonafide solutions)
$\frac{ \psi+1}{ \psi }+\frac{ 14}{ \psi - 7 }=\frac{9 \psi - 7 }{ \psi^2 -7 \psi}$ (one bonafide, one extraneous)
$\frac{ s+1}{ s }+\frac{ 4}{ s - 2 }=\frac{5 s - 2 }{ s^2 -2 s}$ (two extraneous)
Example with Irrational Roots
No every "rational equation" has rational roots. Some have irrational roots such as this example.
$\frac{\mu^2}{\mu^2- \mu - 42}=\frac{3 \mu}{\mu^2+ \mu - 56}$
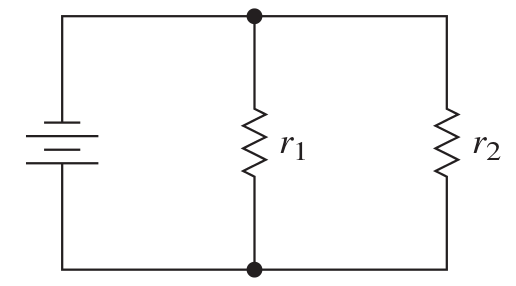
Application: Electrical Resistance
The total resistance $R$ in a parallel circuit with two individual resistors $r_1$ and $r_2$ can be calculated by using the formula $\frac{1}{R}=\frac{1}{r_1}+\frac{1}{r_2}.$ The resistance planned by an electrical technician for a parallel electric circuit with two resistors is $41.2$ $\Omega$. The resistance of $r_2$ must be $6$ times the resistance of $r_1.$ Determine the resistance of each resistor. Round your answer to the nearest hundredth of an ohm.