Arithmetic of Rational Expressions: Rational expressions have their own arithmetic (addition, subtraction, multiplication, and division).
We've added, subtracted, multiplied, and divided rational expressions. Now we're going apply multiple operations at the same time.
Mixing it Up: to perform multiple operations on rational expressions, use the order of operations.
Example: simplify the following rational expression.
$\frac{ 6 \rho - 6 }{ 4 \rho - 5}-\frac{ 3 \rho - 5 }{ 4 \rho ^2 + 3 \rho - 10 } \div \frac{ 5 - 3 \rho } {\rho + 2 }$
Complex Fractions
A complex fraction is a fraction whose numerator and denominator are...
You guessed it!
Fractions!
Example: $\frac{ \frac{k^2-8k+15}{k^2-10k+25} }{ \frac{k^2-6k+9}{11 k^2-275} }$
How Handle Complex Fractions
Method 1: use the tried and true invert and multiply.
$\frac{ \frac{k^2-8k+15}{k^2-10k+25} }{ \frac{k^2-6k+9}{11 k^2-275} }$
$\frac{ 6 \rho - 6 }{ 4 \rho - 5}-\frac{\frac{ 3 \rho - 5 }{ 4 \rho ^2 + 3 \rho - 10 }}{\frac{ 5 - 3 \rho } {\rho + 2 }}$ (this example should look familiar)
Big Fact: If you can get your expression into the "fraction over a fraction" form, you can simply invert and multiply.
How Handle Complex Fractions
Method 2: multiply by a "fancy 1" to get rid of denominators.
$\frac{ \frac{1}{\eta \theta^2}+\frac{1}{\eta^2\theta} }{ \frac{1}{\theta}+\frac{1}{\eta} }$
$\frac{ v-\frac{1}{\phi} }{ \phi-\frac{1}{v} }$
Big Fact: If you can get your expression into the "fraction over a fraction" form, you can simply invert and multiply.
Mixing it Up: Sometimes we need to throw a little bit of both Method 1 and 2 into the mix.
$$\frac{ \frac{1+\frac{p}{\phi}}{1-\frac{p}{\phi}} }{ \frac{p+\phi}{p-\frac{\phi^2}{p}} }$$
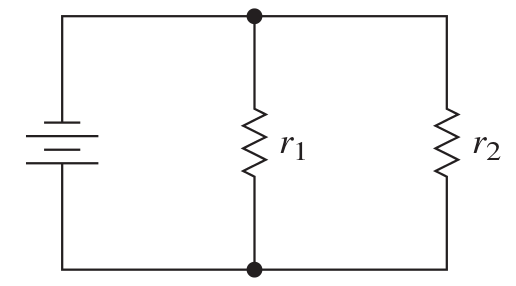
Application of Complex Fractions
Electrical Resistance: The total resistance $R$ in a parallel circuit with two individual resistors $r_1$ and $r_2$ can be calculated by using the formula $$R=\frac{1}{\frac{1}{r_1}+\frac{1}{r_2}}.$$