A Garden Variety Quadratic Equation $ax^2+bx+c=0.$
We are going to solve this equation in general.
But first, let's explore the human side to this equation.
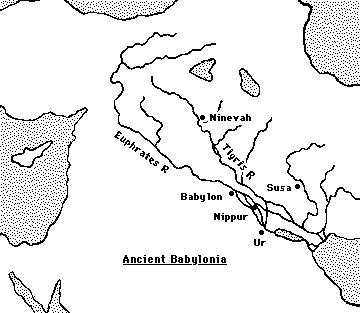
Babylonian Mathematics
Babylon was a mathematically hip society. In particular, by 2000 BC, they had a positional base 60 number system (like our base 10 system) and, interestingly enough, had learned to solve quadratic equations.
Babylonian Mathematics
Fun Fact: In 2000 BC the Babylonians were using a base 60 positional number system (much like our base 10 system) before Roman numerals were even invented!
Below are the 59 symbols the Babylonians used in their system:
Example Converting a Babylonian base 60 number to our base 10 system.
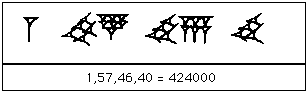
Babylonian Mathematics
Question: How do we know all of this?
Answer: Well I'm glad you asked! The Babylonians adopted from the Sumerians a style of writing on clay tablets cuneiform.
Many of these clay tablets have survived, such as the one pictured below.
Babylonian Mathematics
Many of the tablets concern topics which, although mundane, nevertheless are historically fascinating. For example irrigation systems of the early civilizations in Mesopotamia were of critical importance. Of this Muroi writes:
It was an important task for the rulers of Mesopotamia to dig canals and to maintain them, because canals were not only necessary for irrigation but also useful for the transport of goods and armies. The rulers or high government officials must have ordered Babylonian mathematicians to calculate the number of workers and days necessary for the building of a canal, and to calculate the total expenses of wages of the workers.
Babylonian Mathematics
Thus, problems of length, area, and volume were critical to building and maintaining their civilization.
Here's a problem a scribe wrote in an ancient cuneiform tablet:
The area of a rectangle is
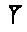(understood to be 60) and its length exceeds its breadth by
(7).
Solution: Compute half of 7, namely
,
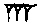
or 3; 30, square it to get
(12; 15).
To this the scribe adds 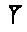or 1, 0 to get
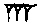
(1; 12, 15).
Take its square root (from a table of squares) to get
(8; 30).
From this subtract 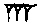(3; 30)
to give the answer 
(5).
Question: Can anyone tell me what this scribe writing about?
Here are the titles of several publications by a scholar who was VERY interested in Babylonian mathematics.
K Muroi, A circular field problem in the late Babylonian metrological-mathematical text W 23291-x, Ganita-Bharati 19 (1-4) (1997), 86-90.
K Muroi, An enigmatic sentence in the old Babylonian table of exponents and logarithms, Historia Sci. (2) 6 (3) (1997), 229-230.
K Muroi, Babylonian mathematics - ancient mathematics written in cuneiform writing (Japanese), in Studies on the history of mathematics (Kyoto, 1998), 160-171.
K Muroi, Extraction of cube roots in Babylonian mathematics, Centaurus 31 (3-4) (1988), 181-188.
K Muroi, Inheritance problems of Babylonian mathematics, Historia Sci. No. 34 (1988), 11-19.
K Muroi, Interest calculation of Babylonian mathematics: new interpretations of VAT 8521 and VAT 8528, Historia Sci. No. 39 (1990), 29-34.
K Muroi, Small canal problems of Babylonian mathematics, Historia Sci. (2) 1 (3) (1992), 173-180.
K Muroi, The expressions of zero and of squaring in the Babylonian mathematical text VAT 7537, Historia Sci. (2) 1 (1) (1991), 59-62.
K Muroi, Two harvest problems of Babylonian mathematics, Historia Sci. (2) 5 (3) (1996), 249-254.
Let's solve $ax^2+bx+c=0$ in general.
When all is said and done, we have $$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}.$$ This is the quadratic formula.
Example Using the quadratic formula, solve the ancient area problem which the Babylonian scribe posed above.
That is, using our base 10 notation, solve $$x^2+7x=60.$$
Examples: Solve the quadratic equation and completely simplify your answer. $$16v^2-24v-6=0$$
Examples: Solve the quadratic equation. Leave the radical unsimplified.
$$9\beta^2=-6\beta+5$$
$$9x^2+12x+4=0$$
$$4t^2-4t=-9$$
Fact: We can use the discriminant to determine the number of solutions a quadratic equations has.
Question: What is the discriminant? D;
Answer: The discriminant is simply the quantity $b^2-4ac$.
If $b^2-4ac>0$, then $ax^2+bx+c=0$ has 2 real number solutions.
If $b^2-4ac=0$, then $ax^2+bx+c=0$ has 1 solution.
If $b^2-4ac<0$, then $ax^2+bx+c=0$ has 0 real number solutions.
Example: How many real number solutions does each quadratic equation have?
$$9\beta^2=-6\beta+5$$
$$9x^2+12x+4=0$$
$$4t^2-4t=-9$$
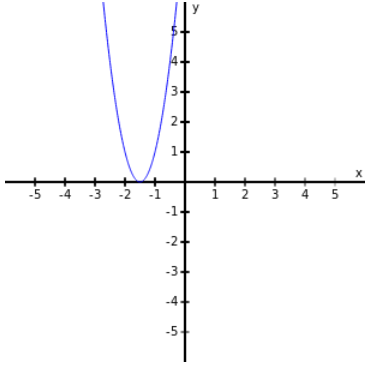
Another Method: Graphs make is much easier to determine the number of real solutions.
The number of $x$-intercepts of the graph $y=ax^2+bx+c$ (exactly where $ax^2+bx+c=0$) is obvious when we look at the graph.
Example: Using the graph below of $y=4x^2+12x+9$, determine how many real number solutions of $4x^2+12x+9=0$.
