The Zero Factor Property: If $ab=0$, then either $a=0$ or $b=0$.
Example: Solve the equation $(2x-3)(x+5)=0$
By the Zero Factor Property (ZFP),
$$2x-3=0 \,\,\,\mbox{ OR }\,\,\,\, x+5=0$$
We conclude that $\displaystyle x=\frac{3}{2}$ OR $x=-5.$
Be sure to check both solutions in the original equation.
Be sure to check both solutions in the original equation.
Example: Solve the equation $x^2-3x+2=0$
Factoring the left hand side,
$$
(x-1)(x-2)=0
$$
which gives
$$
x-1=0 \,\,\, \mbox{ OR }\,\,\, x-2=0
$$
Then $x=1$ OR $x=2.$
Be sure to check both solutions in the original equation.
Be sure to check both solutions in the original equation.
Examples
$56r^2-82r+30=0$
Just like our second example, we factor the left hand side.
$$
2(28r^2-41r+15)=0
$$
Then, by factoring,
$$
2(4r-3)(7r-5)=0
$$
If could only be that $4r-3=0$ or $7r-5=0.$
We conclude that $\displaystyle r=\frac{3}{4}$ or $\displaystyle r=\frac{5}{7}.$
Check
For $\displaystyle r=\frac{3}{4},$ $$ \begin{array}{lll} \displaystyle 56r^2-82r+30&\displaystyle=56\left(\frac{3}{4}\right)^2-82\left(\frac{3}{4}\right)+30 &\mbox{}\\ \displaystyle &\displaystyle=56\cdot \frac{9}{16}-82\cdot \frac{3}{4}+30 &\mbox{}\\ \displaystyle &\displaystyle=7\cdot \frac{9}{2}-41\cdot \frac{3}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle= \frac{63}{2}-\frac{123}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle= \frac{63}{2}- \frac{123}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle=-\frac{60}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle=-30+30 &\mbox{}\\ \displaystyle &\displaystyle=0 \, \checkmark &\mbox{}\\ \end{array} $$ For $\displaystyle r=\frac{5}{7},$ $$ \begin{array}{lll} \displaystyle 56r^2-82r+30&\displaystyle=56\left(\frac{5}{7}\right)^2-82\left(\frac{5}{7}\right)+30 &\mbox{}\\ \displaystyle &\displaystyle=56\cdot \frac{25}{49}-82\cdot \frac{5}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=8\cdot \frac{25}{7}-82\cdot \frac{5}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=\frac{200}{7}- \frac{410}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=-\frac{210}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=-30+30 &\mbox{}\\ \displaystyle &\displaystyle=0 \, \checkmark &\mbox{}\\ \end{array} $$
We conclude that $\displaystyle r=\frac{3}{4}$ or $\displaystyle r=\frac{5}{7}.$
Check
For $\displaystyle r=\frac{3}{4},$ $$ \begin{array}{lll} \displaystyle 56r^2-82r+30&\displaystyle=56\left(\frac{3}{4}\right)^2-82\left(\frac{3}{4}\right)+30 &\mbox{}\\ \displaystyle &\displaystyle=56\cdot \frac{9}{16}-82\cdot \frac{3}{4}+30 &\mbox{}\\ \displaystyle &\displaystyle=7\cdot \frac{9}{2}-41\cdot \frac{3}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle= \frac{63}{2}-\frac{123}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle= \frac{63}{2}- \frac{123}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle=-\frac{60}{2}+30 &\mbox{}\\ \displaystyle &\displaystyle=-30+30 &\mbox{}\\ \displaystyle &\displaystyle=0 \, \checkmark &\mbox{}\\ \end{array} $$ For $\displaystyle r=\frac{5}{7},$ $$ \begin{array}{lll} \displaystyle 56r^2-82r+30&\displaystyle=56\left(\frac{5}{7}\right)^2-82\left(\frac{5}{7}\right)+30 &\mbox{}\\ \displaystyle &\displaystyle=56\cdot \frac{25}{49}-82\cdot \frac{5}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=8\cdot \frac{25}{7}-82\cdot \frac{5}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=\frac{200}{7}- \frac{410}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=-\frac{210}{7}+30 &\mbox{}\\ \displaystyle &\displaystyle=-30+30 &\mbox{}\\ \displaystyle &\displaystyle=0 \, \checkmark &\mbox{}\\ \end{array} $$
$12u^2=32u+35$
$$
\begin{array}{rll}
\displaystyle 12u^2&\displaystyle=32u+35 &\mbox{}\\
\displaystyle 12u^2-32u-35&\displaystyle=0 &\mbox{}\\
\displaystyle (2u-7)(6u+5)&\displaystyle=0 &\mbox{}\\
\displaystyle 2u-7=0 \,\,\, \mbox{ OR }\,\,\,6u+5&\displaystyle=0 &\mbox{}\\
\displaystyle u=\frac{7}{2} \,\,\, \mbox{ OR }\,\,\,u&\displaystyle=-\frac{5}{6} &\mbox{}\\
\end{array}
$$
Check
For $\displaystyle u=\frac{7}{2},$ $$ \begin{array}{rll} \displaystyle 12u^2&\displaystyle=32u+35 &\mbox{}\\ \displaystyle 12\left(\frac{7}{2}\right)^2&\displaystyle=32\left(\frac{7}{2}\right)+35 &\mbox{}\\ \displaystyle 12\cdot \frac{49}{4}&\displaystyle=32\cdot \frac{7}{2}+35 &\mbox{}\\ \displaystyle 3\cdot 49&\displaystyle=16\cdot 7+35 &\mbox{}\\ \displaystyle 147&\displaystyle=147 \, \checkmark &\mbox{}\\ \end{array} $$ For $\displaystyle u=-\frac{5}{6},$ $$ \begin{array}{rll} \displaystyle 12u^2&\displaystyle=32u+35 &\mbox{}\\ \displaystyle 12\left(-\frac{5}{6}\right)^2&\displaystyle=32\left(-\frac{5}{6}\right)+35 &\mbox{}\\ \displaystyle 12\cdot \frac{25}{36}&\displaystyle=-16\cdot \frac{5}{3}+35 &\mbox{}\\ \displaystyle 1\cdot \frac{25}{3}&\displaystyle=- \frac{80}{3}+35 &\mbox{}\\ \displaystyle \frac{25}{3}&\displaystyle= -\frac{80}{3}+\frac{105}{3} &\mbox{}\\ \displaystyle \frac{25}{3}&\displaystyle= \frac{25}{3} \, \checkmark &\mbox{}\\ \end{array} $$
For $\displaystyle u=\frac{7}{2},$ $$ \begin{array}{rll} \displaystyle 12u^2&\displaystyle=32u+35 &\mbox{}\\ \displaystyle 12\left(\frac{7}{2}\right)^2&\displaystyle=32\left(\frac{7}{2}\right)+35 &\mbox{}\\ \displaystyle 12\cdot \frac{49}{4}&\displaystyle=32\cdot \frac{7}{2}+35 &\mbox{}\\ \displaystyle 3\cdot 49&\displaystyle=16\cdot 7+35 &\mbox{}\\ \displaystyle 147&\displaystyle=147 \, \checkmark &\mbox{}\\ \end{array} $$ For $\displaystyle u=-\frac{5}{6},$ $$ \begin{array}{rll} \displaystyle 12u^2&\displaystyle=32u+35 &\mbox{}\\ \displaystyle 12\left(-\frac{5}{6}\right)^2&\displaystyle=32\left(-\frac{5}{6}\right)+35 &\mbox{}\\ \displaystyle 12\cdot \frac{25}{36}&\displaystyle=-16\cdot \frac{5}{3}+35 &\mbox{}\\ \displaystyle 1\cdot \frac{25}{3}&\displaystyle=- \frac{80}{3}+35 &\mbox{}\\ \displaystyle \frac{25}{3}&\displaystyle= -\frac{80}{3}+\frac{105}{3} &\mbox{}\\ \displaystyle \frac{25}{3}&\displaystyle= \frac{25}{3} \, \checkmark &\mbox{}\\ \end{array} $$
Applications and Translation Practice
A rectangular garden has an area $60$ square meters.
The length of the garden is $7$ meters more than the width. Find the length and width of the garden.

Let $W$ be the width, and let $L$ be the length.
Since "length of the garden is $7$ meters more than the width," we may write $ L=W+7 $ and construct the following figure.
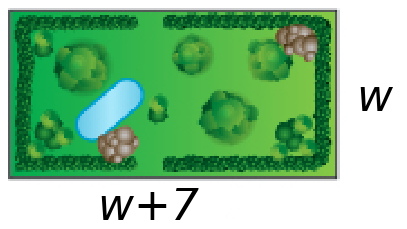
The area, $A,$ of the rectangle is given by the formula $$A=LW.$$ Since we know the area to be $60$ square meters, and $L=W+7,$ we may write $$ 60=(W+7)W $$ Simplifying and rearranging, $$ W^2+7W-60=0 $$ Factoring the left hand side of this equation, $$ (W+12)(W-5)=0 $$ By the ZFP we have $$ W+12=0 \mbox{ or } W-5=0 $$ Then, $W=-12$ or $W=5$
Since a negative length does not make sense for the problem situation, it must be that $W=5$ meters.
Thus, the width is $5$ meters and the length is $12$ meters.
Check
The area is $A=LW=12\cdot 5=60$ square meters. $\checkmark$
The length, $L=12$ is $7$ meters more than the width $W=5$ meters. $\checkmark$
Pythagorean Theorem: Many problems in applied mathematics involve right triangles. In fact, modelling trajectories of projectiles requires an understanding of right-triangle geometry. Thus, a knowledge of the Pythagorean theorem is essential to solving these problems.
For any right triangle, the square of the hypotenuse is the sum of the squares of the legs.

Example
Justine wants to put a deck in the corner of her backyard in the shape of a right triangle.
The hypotenuse will be $17$ feet long.
The length of one side will be $7$ feet less than the length of the other side.
Find the lengths of the sides of the deck.
We shall sketch a picture of this situation.
Let $x$ be one leg of the triangle. Then since the other leg is $7$ less than the other, and since the hypotenuse is $17$ feet, We may draw the following figure.
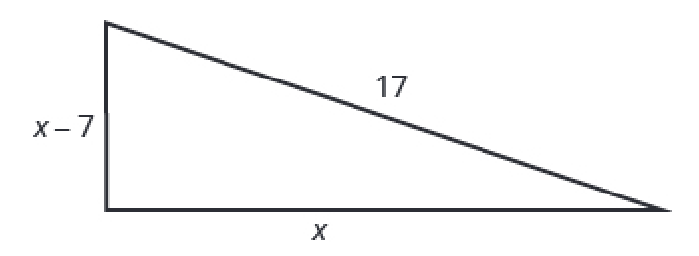
From this figure we may write $$ (x-7)^2+x^2=17^2 $$ Expanding the squares we have $$ x^2-14x+49+x^2=289 $$ which gives $$ 2x^2-14x+49=289 $$ Subtracting $289$ from both sides, $$ 2x^2-14x-240=0 $$ Dividing both sides by $2,$ we have $$ x^2-7x-120=0 $$ Factoring gives $$ (x-15)(x+8)=0 $$ Then, by the ZFP, $$ x=15 \mbox{ or } x=-8. $$ Since a negative length does not make sense for the problem situation, it must be that $x=15$ feet.
Thus the other leg must be $8$ feet.
Check
To make sure the answer is reasonable, we check to see if a right triangle with legs $15$ and $8$ with a hypotenuse of $17$ is possible.
$$ 15^2+8^2=225+64=289=17^2\,\, \checkmark $$
Let $x$ be one leg of the triangle. Then since the other leg is $7$ less than the other, and since the hypotenuse is $17$ feet, We may draw the following figure.

From this figure we may write $$ (x-7)^2+x^2=17^2 $$ Expanding the squares we have $$ x^2-14x+49+x^2=289 $$ which gives $$ 2x^2-14x+49=289 $$ Subtracting $289$ from both sides, $$ 2x^2-14x-240=0 $$ Dividing both sides by $2,$ we have $$ x^2-7x-120=0 $$ Factoring gives $$ (x-15)(x+8)=0 $$ Then, by the ZFP, $$ x=15 \mbox{ or } x=-8. $$ Since a negative length does not make sense for the problem situation, it must be that $x=15$ feet.
Thus the other leg must be $8$ feet.
Check
To make sure the answer is reasonable, we check to see if a right triangle with legs $15$ and $8$ with a hypotenuse of $17$ is possible.
$$ 15^2+8^2=225+64=289=17^2\,\, \checkmark $$
An Honest-to-Goodness Application
Recall, to estimate the population of Oregon $x$ years after $1850,$ we plug in $x$ to the expression.
$$147.3072x^{2}-113.5297x+43724.5175$$
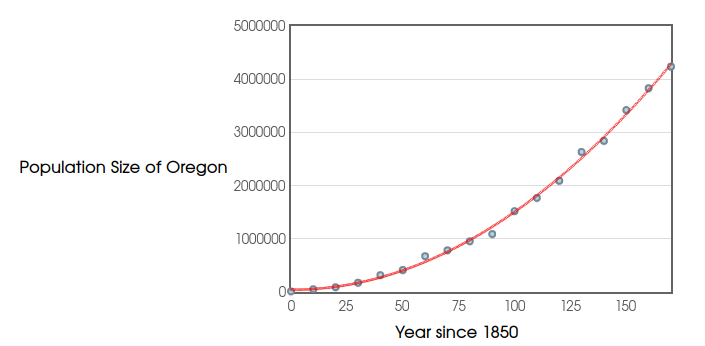
Big Question: When will Oregon's population reach $5$ million?
The question is, for what value of $x$ will the expression $147.3072x^{2}-113.5297x+43724.5175$ equal $\mbox{5,000,000}?$
That is, solve the quadratic equation $$ \begin{array}{lll} \displaystyle 147.3072x^{2}-113.5297x+43724.5175&\displaystyle=\mbox{5,000,000} &\mbox{}\\ \end{array} $$ or $$ 147.3072x^2-113.5297x-\mbox{4,956,275.4825}=0 $$ Care to factor this anyone?
Don't feel bad if the answer is no. In fact, no one in their right mind would do this.
If you move on in mathematics, there are other techniques to handle this equation.
For now, I can tell you that $$ x\approx 183.8137975 \mbox{ years after 1850} $$ That is, we estimate that Oregon's population will hit $5$ million in mid to late $2033.$
That is, solve the quadratic equation $$ \begin{array}{lll} \displaystyle 147.3072x^{2}-113.5297x+43724.5175&\displaystyle=\mbox{5,000,000} &\mbox{}\\ \end{array} $$ or $$ 147.3072x^2-113.5297x-\mbox{4,956,275.4825}=0 $$ Care to factor this anyone?
Don't feel bad if the answer is no. In fact, no one in their right mind would do this.
If you move on in mathematics, there are other techniques to handle this equation.
For now, I can tell you that $$ x\approx 183.8137975 \mbox{ years after 1850} $$ That is, we estimate that Oregon's population will hit $5$ million in mid to late $2033.$