Vocab: A monomial is a product of numbers and variables.
Examples: The following are all monomials.
$-5$
$x$
$A$
$5x$
$7xy$
$\displaystyle \frac{3}{2}x^2 y z^3$
Examples: The following are NOT monomials.
$\displaystyle \frac{1}{x}$
$A^{-1}$
$\displaystyle \frac{5}{x^2}$
$7xy^{-2}$
Single Variable Monomials
A monomial in a single variable has the form $a x^{n}$
Vocab: For the monomial $a x^{n}$, $a$ is called the coefficient, and $n$ is the degree of the monomial.
Example: $4x^7$
Polynomials
Vocab: A polynomial is a sum of monomials.
Examples
$-5$,
$2xy$
$3x^2+2xy-5y^2$
The following is a single variable polynomial: $\displaystyle 2x^5+\frac{4}{5}x^3-x^2+x-9$
Vocab: The highest exponent for a single variable polynomial is called the degree of the polynomial.
More Vocab: Every monomial in a polynomial is called a term.
Example: $\displaystyle 2x^5+\frac{4}{5}x^3-x^2+x-9$
Degree? How many terms?
What is the coefficient on the $3$rd degree term?
One More Piece of Vocab: A polynomial with $1$ term is called a ___________.
One More Piece of Vocab: A polynomial with $2$ terms is called a binomal.
One More Piece of Vocab: A polynomial with $3$ terms is called a trinomal.
For the rest of the quarter, we'll be learning to handle polynomials in either one or two variables.
Today, we learn how to add and subtract polynomials in a single variable.
Adding Polynomials
To add polynomials, simply add like terms.
Like terms have the same degree.
Example: $( -2z^4+ 3z^2+ 2z+ 6)+( 7z^4 -3z^3-9z+ 9)$
Subtracting Polynomials
To subtract polynomials, subtract like terms.
You may also change the sign of every term in the polynomial being subtracted and simply add.
Example: $( 4r^3+ 8r^2 -2r+ 3)-( -3r^2+ 9r+ 2)$
An Honest-to-Goodness Application
Below is a graph of the population of the state of Oregon since $1850.$
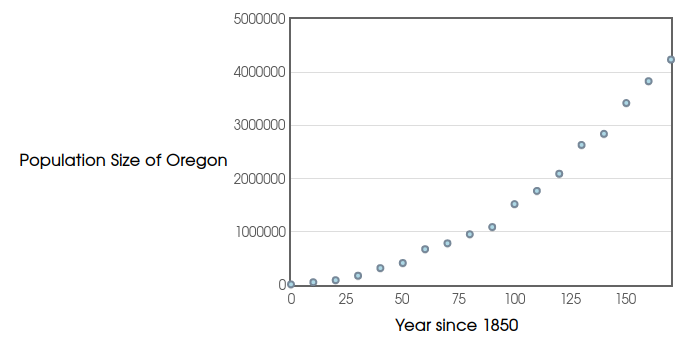
An Honest-to-Goodness Application
Below is a graph of the population of the state of Oregon since $1850.$
The height of the red curve which predicts the population is given by the polynomial expression $$147.3072x^{2}-113.5297x+43724.5175$$
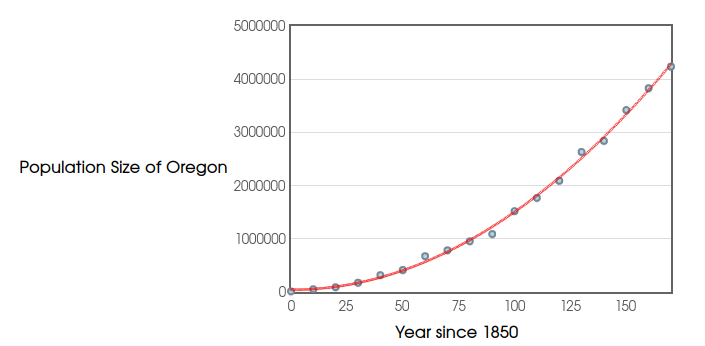
An Honest-to-Goodness Application
For instance, suppose we wanted to estimate the population of Oregon using this expression at $x=150$ years after $1850$ (the year $2000$). Then, $$ \begin{array}{rll} 147.3072x^{2}-113.5297x+43724.5175 &=147.3072(\color{magenta}{150})^{2}-113.5297(\color{magenta}{150})+43724.5175&\mbox{since $x=\color{magenta}{150}$}\\ &=147.3072(22500)-17029.455+43724.5175&\mbox{}\\ &=3314412+26695.0625&\mbox{}\\ &=3341107.0625&\mbox{}\\ \end{array} $$

An Honest-to-Goodness Application
Our estimate, $\mbox{3,341,107},$ compares favorably to the true value of $\mbox{3,421,399}.$
The estimate comes in within $2.3\%$ of the true value.

An Honest-to-Goodness Application
Is anyone here interested in what the model predicts about the population of Oregon in $2030?$

An Honest-to-Goodness Application
Estimate the population of Oregon using the expression at $x=180$ (the year $2030$). $$ \begin{array}{rll} 147.3072x^{2}-113.5297x+43724.5175 &=147.3072(\color{magenta}{180})^{2}-113.5297(\color{magenta}{180})+43724.5175&\mbox{since $x=\color{magenta}{180}$}\\ &=147.3072(32400)-20435.346+43724.5175&\mbox{}\\ &=4772753.28+23289.1715&\mbox{}\\ &=4796042.4515&\mbox{}\\ \end{array} $$ That is, we anticipate that about $\mbox{4,796,042},$ people will be living in Oregon by $2030.$