With equations we are interested in values of $x$ that make statement of equality true.
Today, we find values of $x$ that make inequality statements true.
Like equations, inequalities are are workhorses of applied mathematics.
Examples of Linear Inequalities
$5>-x+3$
$3(-3x-4) \leq -5(5x-1)$
$3x+2<-x+4$
Solutions to Linear Inequalities.
A solution to an inequality is a value of $x$ which makes an inequality statement true.
Solutions to Linear Inequalities.
Example: Verify that $x=1$ is a solution to the inequality $3x-3 \lt 3.$
$3(1)-3=0 \lt 3$ TRUE $\checkmark$
Example: Verify that $x=3$ is NOT a solution to the inequality $3x-3 \lt 3.$
$3(3)-3=6 \lt 3$ FALSE $\times$
Solution Sets to Compound Inequalities
Example: Solve the inequality $3x-3<3$.
Also, graph the solution set and write it in interval notation.

Solution
$$ \begin{array}{rll} \displaystyle 3x-3&\displaystyle\lt 3&\mbox{}\\ \displaystyle 3x-3\color{magenta}{+3}&\displaystyle\lt 3\color{magenta}{+3}&\mbox{addition property of $\color{red}{\mbox{in}}$equality}\\ \displaystyle 3x&\displaystyle\lt 6&\mbox{simplify}\\ \displaystyle \frac{3x}{\color{magenta}{3}}&\displaystyle\lt \frac{6}{\color{magenta}{3}}&\mbox{division property of $\color{red}{\mbox{in}}$equality}\\ \displaystyle x&\displaystyle\lt 2&\mbox{simplify}\\ \end{array} $$ Graphing all $x$ that are less than $2$ on the number line,

We may write the collection of all $x$ less than $2$ as an interval, $(-\infty,2).$
Some Observations About Inequalities
Linear inequalities can have infinitely many solutions.
These solution sets are intervals of real numbers.
For the above reasons, we shall learn the notation for all the types of intervals we may encounter.
Examples
Graph the following intervals and write them in interval notation.
ⓐ $x \leq 1$
ⓑ $x \lt 5$
ⓒ $x \gt - 1$
Solutions
ⓐ $x \leq 1$

$(-\infty,1]$
ⓑ $x \lt 5$

$(-\infty,5)$
ⓒ $x \gt - 1$

$(-1,\infty)$
In General

"$\lt$" and "$\gt$" are denoted by "$($" or "$)$"
"$\leq$" and "$\geq$" are denoted by "$[$" or "$]$"
Example
Solve the inequality $\displaystyle n -\frac{1}{2} \leq \frac{5}{8}$, graph the solution on the number line, and write the solution in interval notation
Solution

The Multiplication and Division Properties of Inequality
We've already used the division property of inequality already when the coefficient on $x$ was positive.
Recall, $$ \begin{array}{rll} \displaystyle 3x-3&\displaystyle\lt 3&\mbox{}\\ \displaystyle 3x-3\color{magenta}{+3}&\displaystyle\lt 3\color{magenta}{+3}&\mbox{addition property of $\color{red}{\mbox{in}}$equality}\\ \displaystyle 3x&\displaystyle\lt 6&\mbox{simplify}\\ \displaystyle \frac{3x}{\color{magenta}{3}}&\displaystyle\lt \frac{6}{\color{magenta}{3}}&\mbox{division property of $\color{red}{\mbox{in}}$equality}\\ \displaystyle x&\displaystyle\lt 2&\mbox{simplify}\\ \end{array} $$
Dire Warning: When we multiply or divide both sides of an inequality by a negative number, the inequality sign flips
Example
It is certainly true that $-2 \lt 3.$
Multiplying both sides by $-4$ gives $$ (-4)(-2)\gt (-4)(3) $$ or $$ 8 \gt -12 $$ The inequality sign must flip in order to maintain a true statement.
Example
Solve the inequality $-10a \geq 50,$ graph the solution on the number line, and write the solution in interval notation.
Solution
$$ \begin{array}{rll} \displaystyle -10a&\displaystyle\geq 50&\mbox{}\\ \displaystyle \frac{-10a}{\color{red}{-10}}&\displaystyle\leq \frac{50}{\color{red}{-10}}&\mbox{division property of $\color{red}{\mbox{in}}$equality: the inequality sign flips!}\\ \displaystyle a&\displaystyle\leq -5&\mbox{simplify}\\ \end{array} $$
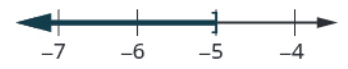
$(-\infty,-5]$
Examples
Solve the inequalities graph their solution on the number line, and write the solutions in interval notation.
(a) $\displaystyle -20 \lt \frac{4}{5}u$
(b) $\displaystyle \frac{t}{-2} \geq 8$
Solutions
Solve the inequalities graph their solution on the number line, and write the solutions in interval notation.
(a)
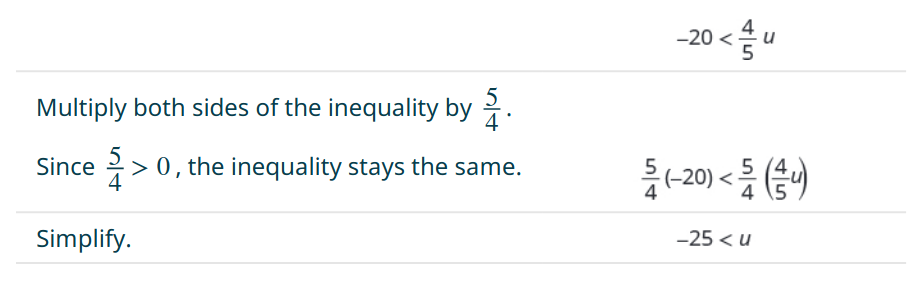

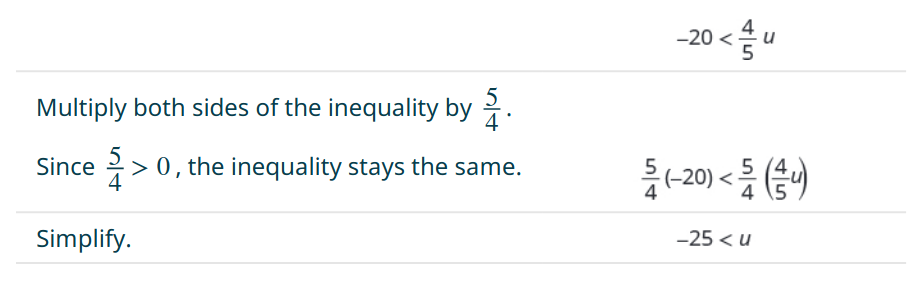

(b)
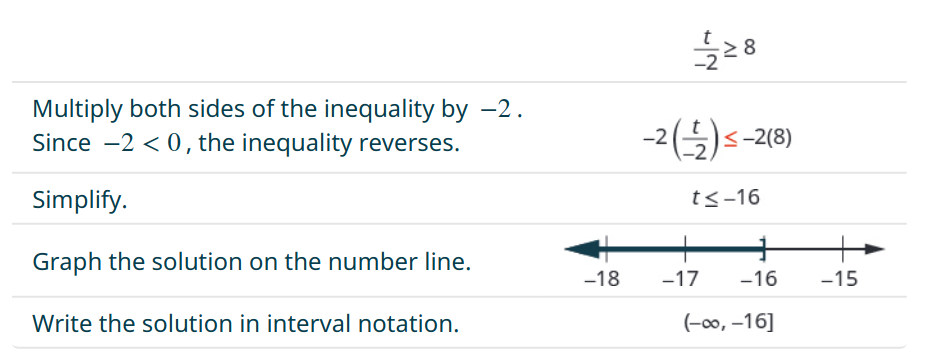
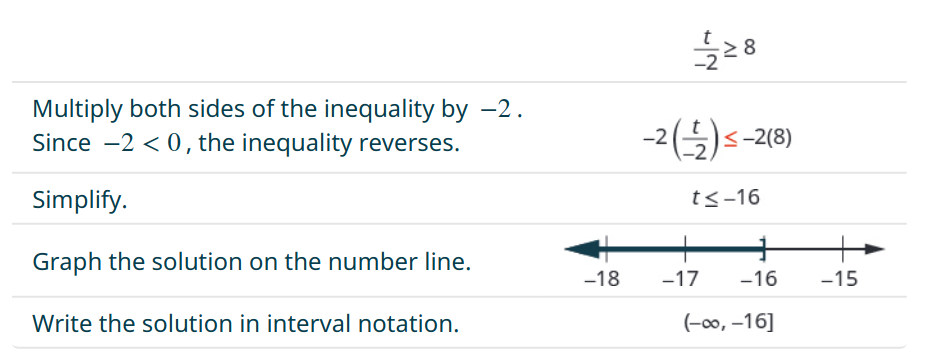
With the above, may now solve any linear inequality!


Example
Solve the inequality graph its solution on the number line, and write the solution in interval notation.
$8p + 3(p - 12) \gt 7p - 28$
Solutions


Gremlin Case #1
Sometimes an inequality can be true for all $x.$ For example $x+1\gt x$ is true for all $x.$
The graph and interval in this case are as follows.

$(-\infty,\infty)$
Gremlin Case #2
On the other hand, an inequality can be false for all $x.$ For example $x+1\lt x$ is false for all $x.$
The graph and interval in this case are as follows.

There is no solution. No points light up.
Gremlin Examples
Solve the inequalities graph their solution on the number line, and write the solutions in interval notation.
(a) $\displaystyle 8x - 2(5 - x) \lt 4(x + 9) + 6x$
(b) $\displaystyle \frac{1}{3}a-\frac{1}{8}a \gt \frac{5}{24}a+\frac{3}{4}$
Gremlin Solutions
(a)


(b)


Translating Inequality Statements
Example
Translate and solve. Then write the solution in interval notation and graph on the number line.
Thirty less than $x$ is at least $45.$
Solution

An Honest-to-Goodness Application
Many electronic electronic devices, such as phones, tablets, laptops, etc., require a power adaptor that can run and charge the device when plugged in.
The correct power adaptor requires a minimum amount current to function properly.
This minimum amount of current is called the minimal load.
Suppose we have a $9$ volt AC power adaptor with a minimal load rating of $0.6$ amperes as seen below.

What is the largest resistance of a device that this power supply can reliably handle?
Solution
Since the minimal load is $0.6$ amperes, we know that $I \geq 0.6.$
Then, $IR \geq 0.6 R$ multiplying both sides of the above by $R.$ (Multiplication property!)
By Ohm's law $V=IR,$ so $V \geq 0.6 R.$
Since the voltage of the power supply is $9$ volts, the inequality we need to solve is $9 \geq 0.6 R.$
Thus, $$ \begin{array}{rll} \displaystyle 9&\displaystyle\geq 0.6 R&\mbox{}\\ \displaystyle \frac{9}{\color{magenta}{0.6}}&\displaystyle\geq \frac{0.6R}{\color{magenta}{0.6}}&\mbox{division property of $\color{red}{\mbox{in}}$equality}\\ \displaystyle 15&\displaystyle\geq R&\mbox{simplify}\\ \end{array} $$ Equivalently, $\displaystyle R \leq 15.$
So, any device with a total resistance of $15$ ohms or less will allow the adaptor to function properly.