Where there's a formula, there's an application of mathematical ideas.
When the universe hands us a mess of information and leaves us to sort our the rest of the details, formulas are a handy guide for putting those puzzle pieces together.
Formulas
A formula expresses a relationship between two or more variable quantities.
A Parade of Formulas
$\displaystyle A=\frac{1}{2}bh$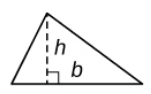 
Area of a Triangle
$\displaystyle F=\frac{GMm}{r^2}$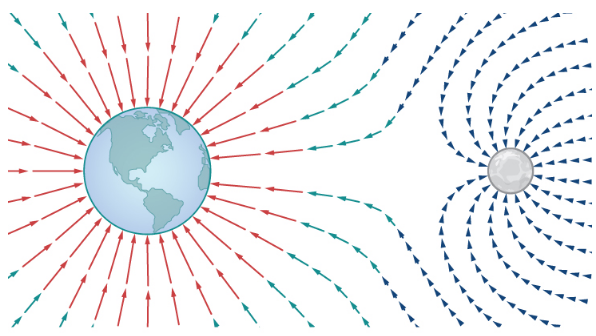
Newton's Law of Gravitation
$\displaystyle V=\frac{1}{3}\pi r^2 h$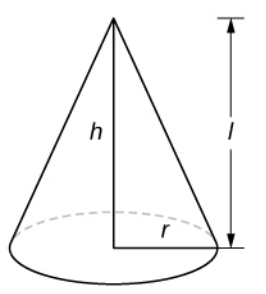
Volume of a Cone
$\displaystyle F=\frac{9}{5}C+32$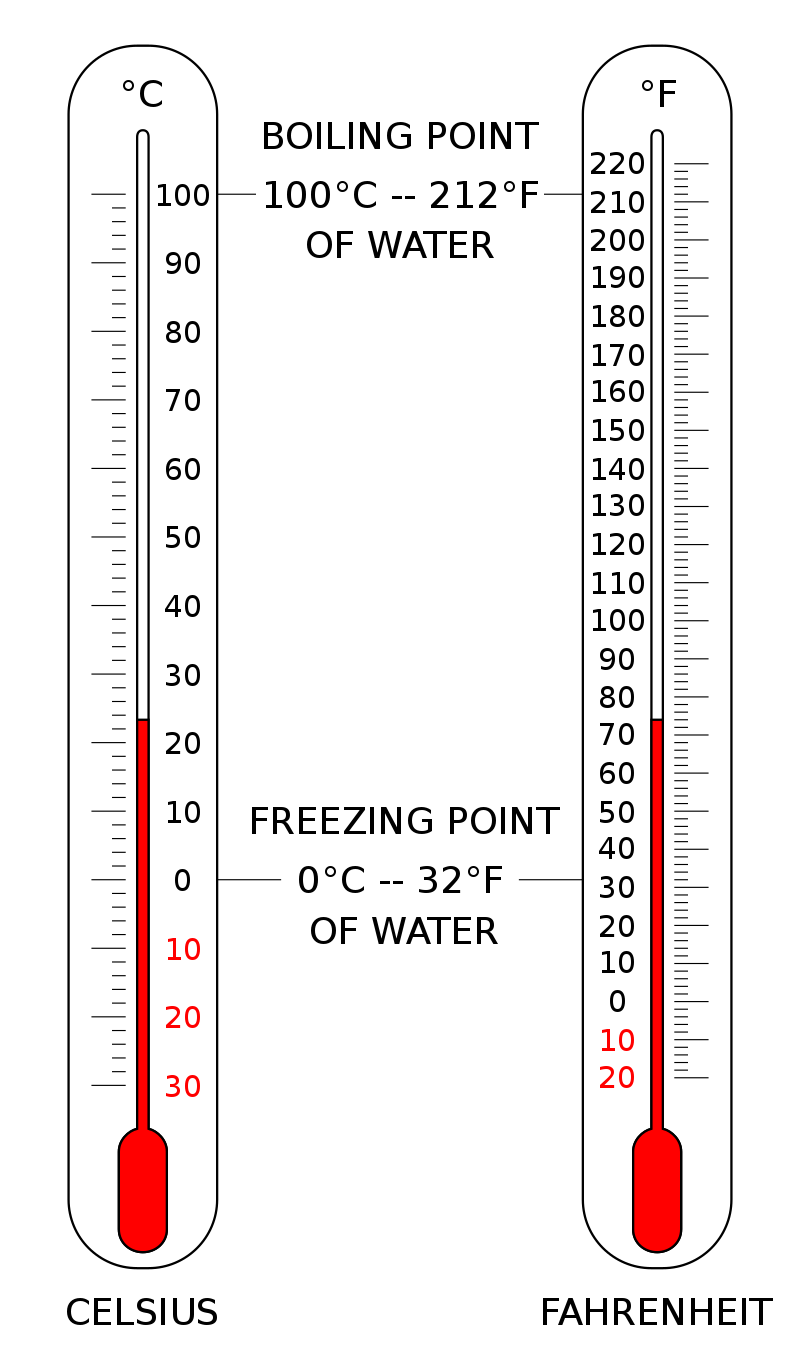
Fahrenheit and Celsius
$\displaystyle I=\frac{V}{R}$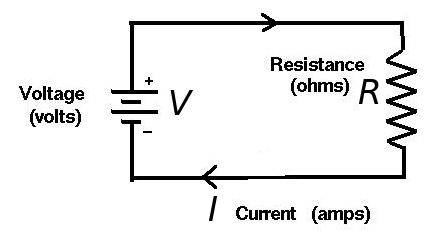
Ohm's Law
$\displaystyle A=Prt$
Simple Interest
$\displaystyle A=P\left(1+\frac{r}{n}\right)^{nt}$
Compound Interest
$\displaystyle PV=nRT$
Ideal Gas Law
Area of a Triangle
$\displaystyle F=\frac{GMm}{r^2}$
Newton's Law of Gravitation
$\displaystyle V=\frac{1}{3}\pi r^2 h$
Volume of a Cone
$\displaystyle F=\frac{9}{5}C+32$
Fahrenheit and Celsius
$\displaystyle I=\frac{V}{R}$
Ohm's Law
$\displaystyle A=Prt$
Simple Interest
$\displaystyle A=P\left(1+\frac{r}{n}\right)^{nt}$
Compound Interest
$\displaystyle PV=nRT$
Ideal Gas Law
Example
Solve the formula $\displaystyle A=\frac{1}{2}bh$ for $h.$
Solution
$$ \begin{array}{lll} \displaystyle A&\displaystyle= \frac{1}{2}bh&\mbox{original formula}\\ \displaystyle \color{magenta}{2\cdot} A&\displaystyle= \color{magenta}{2\cdot}\frac{1}{2}bh&\mbox{multiplication property}\\ \displaystyle 2A&\displaystyle= bh&\mbox{simplify}\\ \displaystyle \frac{2A}{\color{magenta}{b}}&\displaystyle= \frac{bh}{\color{magenta}{b}}&\mbox{division property}\\ \displaystyle \frac{2A}{b}&\displaystyle= h&\mbox{simplify}\\ \end{array} $$ Thus, $$ h=\frac{2A}{b} $$
Strategy for Solving Formulas for a Specified Variable
Step 1: If necessary, multiply each term by a single quantity which clears any fractions or decimals for all terms.
Step 2: If necessary, gather all terms with the variable you want to solve for on the "variable side" of the equation. All other terms go on the "other" side of the equation.
Step 3: If necessary, combine like terms on the variable side. (This may mean using the distributive property in reverse.)
Step 4: Divide both sides by the quantity multiplying the variable you want to solve for.
Step 5: If necessary, simplify the resulting expression on the other side.
Example
Solve the equation $\displaystyle \frac{1}{2}x+\frac{2}{3}y=1$ for $y$.
Solution
$$ \begin{array}{rll} \displaystyle \frac{1}{2}x+\frac{2}{3}y&\displaystyle= 1&\mbox{original formula}\\ \displaystyle \color{magenta}{6\cdot}\left(\frac{1}{2}x+\frac{2}{3}y\right) &\displaystyle= \color{magenta}{6\cdot}1&\mbox{multiplication property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle \color{magenta}{6\cdot}\frac{1}{2}x+\color{magenta}{6\cdot}\frac{2}{3}y&\displaystyle= 6&\mbox{distribute}\\ \displaystyle 3x+4y&\displaystyle= 6&\mbox{simplify}\\ \displaystyle 3x+4y\color{magenta}{-3x}&\displaystyle= 6\color{magenta}{-3x}&\mbox{subtraction property ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 4y&\displaystyle= 6-3x&\mbox{simplify LHS ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle \frac{4y}{\color{magenta}{4}}&\displaystyle= \frac{6-3x}{\color{magenta}{4}}&\mbox{division property ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle y&\displaystyle= \frac{6-3x}{4}&\mbox{simplify LHS ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle y&\displaystyle= \frac{3}{2}-\frac{3}{4}x&\mbox{simplify RHS ($\color{blue}{\mbox{Step 5}}$)}\\ \end{array} $$
Example: Simple Interest
A loan shark gives simple interest loans at a weekly rate of $16$ percent.
If after $5$ weeks the loan shark collects a vig (the amount of interest made) of $\$28.80,$ what was the principal amount of the loan?
Round your answer to the nearest cent.
Solution
The Simple-Interest Formula is $I=Prt.$
With the information the problem gives, $I=28.80,$ $r=0.16,$ and $t=5.$
The unknown is the principal amount of the loan, $P.$
So, $28.80=P\cdot 0.16 \cdot 5.$ Then $$ \begin{array}{lll} \displaystyle 28.80&\displaystyle=0.8 P &\mbox{}\\ \displaystyle \frac{28.80}{\color{magenta}{0.8}}&\displaystyle=\frac{0.8 P}{\color{magenta}{0.8}} &\mbox{division property}\\ \displaystyle 36&\displaystyle=P &\mbox{simplify}\\ \end{array} $$
Check $$ \begin{array}{lll} \displaystyle 28.80&\displaystyle= 0.8 \cdot \color{magenta}{P}&\mbox{oringinal equation}\\ \displaystyle 28.80&\displaystyle= 0.8 \cdot \color{magenta}{36}&\mbox{since $\color{magenta}{P=36}$}\\ \displaystyle 28.80&\displaystyle= 28.80&\mbox{$\checkmark$}\\ \end{array} $$ The principal amount of the loan was $\$36.$
Example
Solve the simple interest formula $I=Prt$ for $P.$
Solution
$$ \begin{array}{rll} \displaystyle I&\displaystyle=Prt &\mbox{original formula}\\ \displaystyle \frac{I}{\color{magenta}{rt}}&\displaystyle=\frac{Prt}{\color{magenta}{rt}} &\mbox{division property}\\ \displaystyle \frac{I}{rt}&\displaystyle=P &\mbox{simplify RHS}\\ \end{array} $$ Thus, $$ P=\frac{I}{rt} $$
Something to Consider
Notice we could have have answered the previous question by solving for $P$ first and then "plugging in" the values: $$ \begin{array}{lcl} \displaystyle P&\displaystyle= \frac{I}{rt}&\mbox{formula solved for $P$}\\ \displaystyle &\displaystyle= \frac{28.80}{0.16\cdot 5}&\mbox{since $I=28.80,$ $r=0.16,$ and $t=5.$}\\ \displaystyle &\displaystyle= 36&\mbox{simplify}\\ \end{array} $$
Uniform Motion
When objects move at a constant, unchanging speed, they exhibit uniform motion.
The distance $d$ travelled by an object going at a constant speed $r$ for a time $t$ is given by the formula $$ d=rt $$ Example: You're heading up the I-5 corridor with the cruise control set for $65$ miles per hour. How far will you have travelled after $2$ hours?
Solution: In the above scenario, $r=65$ mph and $t=2$ hours. Then, $$ d=rt=65 \cdot 2 = 130 $$ Thus, after $2$ hours, you will have travelled $130$ miles.
Example
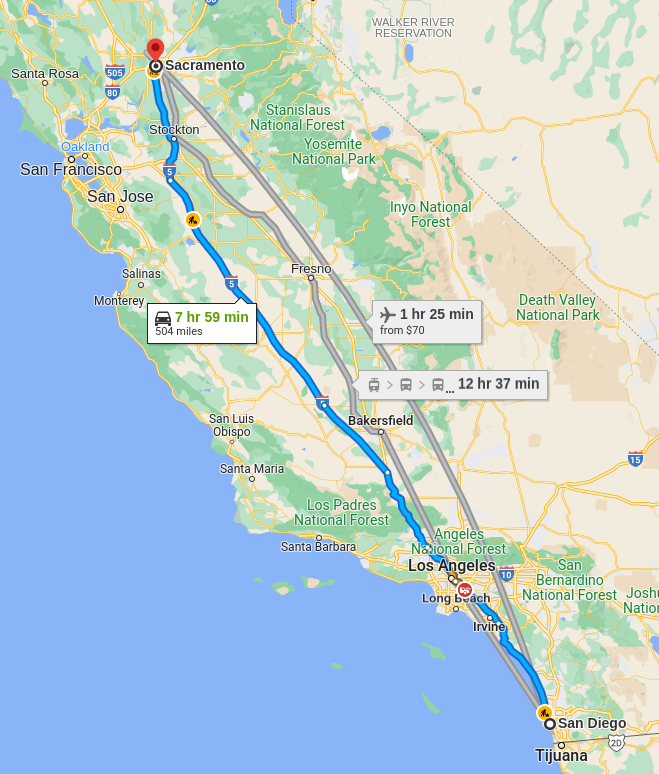
Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of $520$ miles.
If he can drive at a steady rate of $65$ miles per hour, how many hours will the trip take?
Solution
Since the problem involves uniform motion, we use the formula $d=rt.$
From the information the problem gives, $d=520$ miles and $r=65$ miles per hour.
Then, $$ \begin{array}{lll} \displaystyle d&\displaystyle= rt&\mbox{uniform-motion formula}\\ \displaystyle 520&\displaystyle=65t &\mbox{since $d=520$ and $r=65$}\\ \displaystyle \frac{520}{\color{magenta}{65}}&\displaystyle=\frac{65t}{\color{magenta}{65}} &\mbox{division property}\\ \displaystyle 8&\displaystyle=t &\mbox{division property}\\ \end{array} $$
Check
$$ \begin{array}{lll} \displaystyle 520&\displaystyle= 65\cdot \color{magenta}{t}&\mbox{oringinal equation}\\ \displaystyle 520&\displaystyle= 65 \cdot \color{magenta}{8}&\mbox{since $\color{magenta}{t=8}$}\\ \displaystyle 520&\displaystyle= 520&\mbox{$\checkmark$}\\ \end{array} $$ Thus, Rey's trip lasted $8$ hours.
Example
(a) Solve the Ohm's Law formula $\displaystyle I=\frac{V}{R}$ for $V.$
(b) Solve the resulting equation from part (a) for $R.$
(c) What is the resistance of a $75$ watt bulb that draws a current of $0.65$ amperes at $115$ volts?
Solution
(a) $$ \begin{array}{rll} \displaystyle I&\displaystyle=\frac{V}{R} &\mbox{original formula}\\ \displaystyle I\color{magenta}{\cdot R}&\displaystyle=\frac{V}{R}\color{magenta}{\cdot R} &\mbox{multiplication property}\\ \displaystyle IR&\displaystyle=V &\mbox{simplify RHS}\\ \end{array} $$ Thus, $V=IR.$
(b) $$ \begin{array}{rll} \displaystyle V&\displaystyle=IR &\mbox{original formula}\\ \displaystyle \frac{V}{\color{magenta}{I}}&\displaystyle=\frac{IR}{\color{magenta}{I}} &\mbox{division property}\\ \displaystyle \frac{V}{I}&\displaystyle=R &\mbox{simplify RHS}\\ \end{array} $$ Thus, $$ R=\frac{V}{I} $$ (c) We will use the rearranged formula obtained in part (b) to calculate the resistance.
The problem gives us that $I=0.65$ amperes and $V=115$ volts.
Then, $$ \begin{array}{rll} \displaystyle R&\displaystyle= \frac{V}{I}&\mbox{formula solved for $R$}\\ \displaystyle &\displaystyle= \frac{115}{0.65}&\mbox{since $V=115$ and $I=0.65$}\\ \displaystyle &\displaystyle= 176.923076923&\mbox{simplify}\\ \displaystyle &\displaystyle\approx 176.9&\mbox{the symbol $\approx$ means approximately equal to}\\ \end{array} $$ Thus, the resistance of the bulb is approximately $176.9$ ohms.