We continue our study of equations by adding one more, teensy-weensy little step to what we did last time...
Example
Solve the equation $-6(x+3)=24.$
Solution
$$ \begin{array}{rll} \displaystyle -6(x+3)&\displaystyle= 24 &\mbox{original equation}\\ \displaystyle -6x-18&\displaystyle= 24&\mbox{simplify LHS with distributive property}\\ \displaystyle -6x-18\color{magenta}{+18}&\displaystyle= 24\color{magenta}{+18}&\mbox{addition property of equality}\\ \displaystyle -6x&\displaystyle= 42&\mbox{simplify}\\ \displaystyle \frac{-6x}{\color{magenta}{-6}}&\displaystyle= \frac{42}{\color{magenta}{-6}}&\mbox{division property of equality}\\ \displaystyle x&\displaystyle=-7&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle -6(\color{magenta}{x}+3)&\displaystyle= 24 &\mbox{original equation}\\ \displaystyle -6(\color{magenta}{(-7)}+3)&\displaystyle= 24 &\mbox{since $\color{magenta}{x=-7}$}\\ \displaystyle -6(-4)&\displaystyle= 24 &\mbox{}\\ \displaystyle 24&\displaystyle= 24 &\mbox{$\checkmark$}\\ \end{array} $$
The teensy-weensy little step we added is to simplify one or both sides of the equation first.
General Strategy for Solving Equations
Step 1: Simplify each side of the equation as much as possible.
Step 2: Collect the variable terms to the "variable" side of the equation, using the Addition or Subtraction Property of Equality.
Step 3: Collect all the constants to the "constant" side of the equation, using the Addition or Subtraction Property of Equality.
Step 4: Make the coefficient of the variable equal $1,$ using the Multiplication or Division Property of Equality.
Step 5: Check the solution by substituting it into the original equation.
Example
Solve the equation $\displaystyle \frac{2}{3}(6m-3)=8-m.$
Solution
$$ \begin{array}{rll} \displaystyle \frac{2}{3}(6m-3)&\displaystyle= 8-m &\mbox{original equation}\\ \displaystyle 4m-2&\displaystyle= 8-m&\mbox{simplify LHS with distributive property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 4m-2\color{magenta}{+m}&\displaystyle= 8-m\color{magenta}{+m}&\mbox{addition property of equality ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 5m-2&\displaystyle= 8&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 5m-2\color{magenta}{+2}&\displaystyle= 8\color{magenta}{+2}&\mbox{addition property of equality ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle 5m&\displaystyle= 10&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{5m}{\color{magenta}{5}}&\displaystyle= \frac{10}{\color{magenta}{5}}&\mbox{division property of equality ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle x&\displaystyle=2&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle \frac{2}{3}(6\color{magenta}{m}-3)&\displaystyle= 8-\color{magenta}{m} &\mbox{original equation}\\ \displaystyle\frac{2}{3}(6\color{magenta}{(2)}-3)&\displaystyle= 8-\color{magenta}{2}&\displaystyle= 24 &\mbox{since $\color{magenta}{m=2}$}\\ \displaystyle \frac{2}{3}(12-3)&\displaystyle= 6 &\mbox{}\\ \displaystyle \frac{2}{3}(9)&\displaystyle= 6 &\mbox{}\\ \displaystyle 6&\displaystyle= 6 &\mbox{$\checkmark$}\\ \end{array} $$
Example
Solve the equation $\displaystyle 4(x - 1) - 2 = 5(2x + 3) + 6 .$
Solution
$$ \begin{array}{rll} \displaystyle 4(x - 1) - 2&\displaystyle= 5(2x + 3) + 6 &\mbox{original equation}\\ \displaystyle 4x - 4 - 2&\displaystyle= 10x + 15 + 6 &\mbox{simplify LHS and RHS with distributive property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 4x - 6&\displaystyle= 10x+21 &\mbox{simplify by combining like terms($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 4x - 6\color{magenta}{-4x}&\displaystyle=10x+21\color{magenta}{-4x}&\mbox{subtraction property of equality ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle -6&\displaystyle= 6x+21&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle -6\color{magenta}{-21}&\displaystyle= 6x+21\color{magenta}{-21}&\mbox{subtraction property of equality ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle -27m&\displaystyle= 6x&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{-27}{\color{magenta}{6}}&\displaystyle= \frac{6x}{\color{magenta}{6}}&\mbox{division property of equality ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle -\frac{9}{2}&\displaystyle=x&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle 4(\color{magenta}{x}-1)-2&\displaystyle= 5(2\color{magenta}{x}+3)+6 &\mbox{original equation}\\ \displaystyle 4\left(\color{magenta}{-\frac{9}{2}}-1\right)-2&\displaystyle= 5\left(2\color{magenta}{\left(-\frac{9}{2}\right)}+3\right)+6&\mbox{since $\displaystyle \color{magenta}{x=\frac{9}{2}}$}\\ \displaystyle 4\left(-\frac{11}{2}\right)-2&\displaystyle= 5(-9+3)+6 &\mbox{}\\ \displaystyle -22-2&\displaystyle= 5(-6) +6&\mbox{}\\ \displaystyle -24&\displaystyle= -30 +6&\mbox{}\\ \displaystyle -24&\displaystyle= -24 &\mbox{$\checkmark$}\\ \end{array} $$
Example
Solve the equation $\displaystyle 10[3 - 8(2s - 5)] = 15(40 - 5s).$
Solution
$$ \begin{array}{rll} \displaystyle 10[3 - 8(2s - 5)]&\displaystyle= 15(40 - 5s) &\mbox{original equation}\\ \displaystyle 10[3 - 16s \color{red}{+}40]&\displaystyle= 600-75s &\mbox{simplify LHS and RHS with distributive property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 10[43 - 16s]&\displaystyle= 600-75s &\mbox{simplify by combining like terms ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 430 - 160s&\displaystyle= 600-75s &\mbox{simplify LHS with distributive property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 430 - 160s\color{magenta}{+160s}&\displaystyle=600-75s\color{magenta}{+160s}&\mbox{addition property of equality ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 430&\displaystyle= 600+85s&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 430\color{magenta}{-600}&\displaystyle= 600+85s\color{magenta}{-600}&\mbox{subtraction property of equality ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle -170&\displaystyle= 85s&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{-170}{\color{magenta}{85}}&\displaystyle= \frac{85s}{\color{magenta}{85}}&\mbox{division property of equality ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle -2&\displaystyle=s&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle 10[3 - 8(2\color{magenta}{s} - 5)]&\displaystyle= 15(40 - 5\color{magenta}{s}) &\mbox{original equation}\\ \displaystyle 10[3 - 8(2\color{magenta}{(-2)} - 5)]&\displaystyle= 15(40 - 5\color{magenta}{(-2)})&\mbox{since $\displaystyle \color{magenta}{s=-2}$}\\ \displaystyle 10[3 - 8(-4 - 5)]&\displaystyle= 15(40 - (-10))&\mbox{}\\ \displaystyle 10[3 - 8(-9)]&\displaystyle= 15(40 +10)&\mbox{}\\ \displaystyle 10[3 - (-72)]&\displaystyle= 15(50)&\mbox{}\\ \displaystyle 10[3 +72]&\displaystyle= 750&\mbox{}\\ \displaystyle 10[75]&\displaystyle= 750&\mbox{}\\ \displaystyle 750&\displaystyle= 750 &\mbox{$\checkmark$}\\ \end{array} $$
Example
Solve the equation $\displaystyle 0.36(100n + 5) = 0.6(30n + 15).$
Solution
$$ \begin{array}{rll} \displaystyle 0.36(100n + 5)&\displaystyle= 0.6(30n + 15) &\mbox{original equation}\\ \displaystyle 36n+1.8&\displaystyle= 18n+9 &\mbox{simplify LHS and RHS with distributive property ($\color{blue}{\mbox{Step 1}}$)}\\ \displaystyle 36n+1.8\color{magenta}{-18n}&\displaystyle=18n+9\color{magenta}{-18n}&\mbox{subtraction property of equality ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 18n+1.8&\displaystyle= 9&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 18n+1.8\color{magenta}{-1.8}&\displaystyle= 9\color{magenta}{-1.8}&\mbox{subtraction property of equality ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle 18n&\displaystyle= 7.2&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{18n}{\color{magenta}{18}}&\displaystyle= \frac{7.2}{\color{magenta}{18}}&\mbox{division property of equality ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle n&\displaystyle=0.4&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle 0.36(100\color{magenta}{n} + 5)&\displaystyle= 0.6(30\color{magenta}{n} + 15) &\mbox{original equation}\\ \displaystyle 0.36(100\color{magenta}{(0.4)} + 5)&\displaystyle= 0.6(30\color{magenta}{(0.4)} + 15)&\mbox{since $\displaystyle \color{magenta}{n=0.4}$}\\ \displaystyle 0.36(40 + 5)&\displaystyle= 0.6(12 + 15)&\mbox{}\\ \displaystyle 0.36(45)&\displaystyle= 0.6(27)&\mbox{}\\ \displaystyle 16.2&\displaystyle= 16.2 &\mbox{$\checkmark$}\\ \end{array} $$
Types of Equations
Not all equations are created equal.
For example, the equation $2x=4$ has a single solution.
The equation $x+x=2x$ has infinitely many solutions since it is true for all $x.$
The equation $x=x+1$ has no solutions since there is no value of $x$ that makes it true.
Conditional Equations
An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation.
All of the examples we have looked at today are conditional equations since they all have a single solution.
Identities
An equation that is true for any value of the variable is called an identity.
The solution of an identity is all real numbers
To tell if an equation is an identity, try solving it. If you get a true statement like $0=0,$ or $2=2,$ or something like that, then you have an identity on your hands.
Example: $6(2n - 1) + 3 = 2n - 8 + 5(2n + 1)$

Contradictions
An equation that is false for any value of the variable is called an contradiction.
That is, there is no real number which solves a contradiction.
To tell if an equation is an contradiction, try solving it. If you get a bald-faced lie like $0=1,$ or $1=2,$ or something like that, then you have an contradiction on your hands.
Example: $5m + 3(9 + 3m) = 2(7m - 11)$


Honest-to-Goodness Application
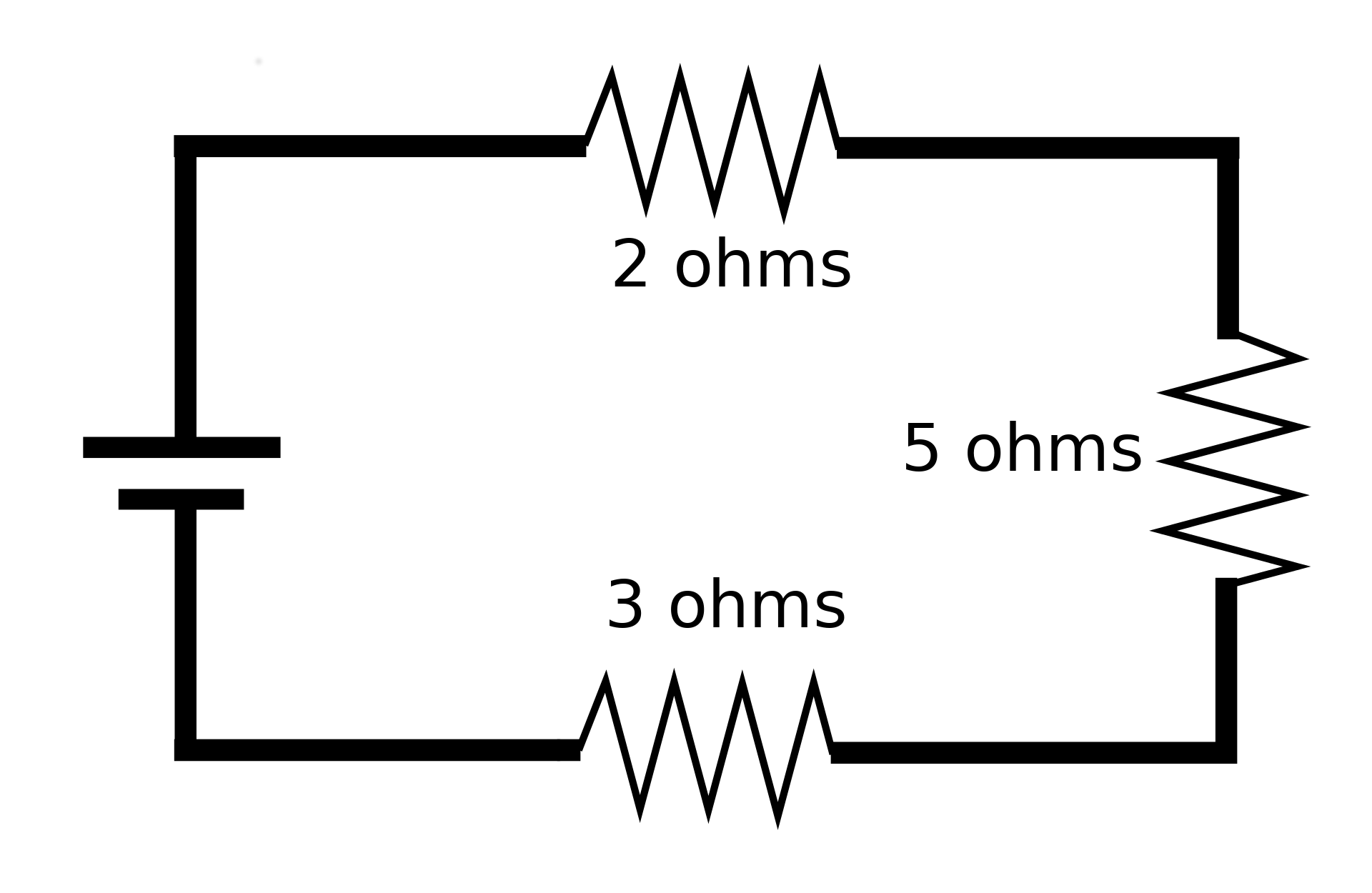
The total resistance of a circuit is the sum of the individual resistances.
For example, total resistances of the circuit below is $2+5+3=10$ ohms.
Honest-to-Goodness Application
Ohm's Law is often stated as $\displaystyle I=\frac{V}{R},$ but it can also be written as $$ IR=V $$ Thus, for the circuit below, $$I\cdot 10=V$$

Honest-to-Goodness Application
A $60$-watt and a $100$-watt lightbulb are wired in series as seen below.
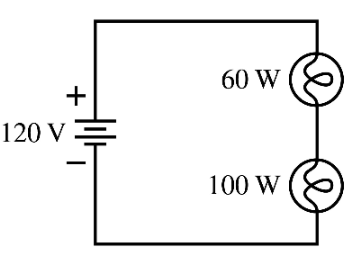
Suppose that $120$-volt household circuit is drawing a current of $\displaystyle 0.3125$ amperes.
We also know that the resistance of the $100$-watt light bulb is $100$ ohms less than the $60$-watt light bulb.
What is the resistance of the $60$-watt bulb?
Solution
Let $r$ be the resistance of the $60$-watt light bulb.
Then, the resistance of the $100$-watt bulb is $r-100$ since "resistance of the $100$-watt light bulb is $100$ ohms less than the $60$-watt light bulb. "
The total resistance, $R,$ of the circuit is then $$ \begin{array}{cccc} R&=&\mbox{Resistance 60-watt bulb}&+&\mbox{Resistance 100-watt bulb}\\ &=&r &+& r-100\\ &=&&2r-100&&\\ \end{array} $$ Ohm's Law stated as $IR=V,$ along with the information given, then gives $$ 0.3125(2r-100)=120 $$ We now solve the equation. $$ \begin{array}{rll} \displaystyle 0.3125(2r-100)&\displaystyle= 120 &\mbox{original equation}\\ \displaystyle 0.625r-31.25&\displaystyle= 120 &\mbox{simplify LHS with distributive property}\\ \displaystyle 0.625r-31.25\color{magenta}{+31.25}&\displaystyle=120\color{magenta}{+31.25}&\mbox{addition property of equality}\\ \displaystyle 0.625r&\displaystyle= 151.25&\mbox{simplify}\\ \displaystyle \frac{0.625r}{\color{magenta}{0.625}}&\displaystyle= \frac{151.25}{\color{magenta}{0.625}}&\mbox{division property of equality}\\ \displaystyle r&\displaystyle=242&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 0.3125(2\color{magenta}{r}-100)&\displaystyle= 120 &\mbox{original equation}\\ \displaystyle 0.3125(2\color{magenta}{(242)}-100)&\displaystyle= 120&\mbox{since $\displaystyle \color{magenta}{r=242}$}\\ \displaystyle 0.3125(484-100)&\displaystyle= 120&\mbox{}\\ \displaystyle 0.3125(384)&\displaystyle= 120&\mbox{}\\ \displaystyle 120&\displaystyle= 120 &\mbox{$\checkmark$}\\ \end{array} $$ Thus, the resistance of the $60$-watt light bulb is $242$ ohms.
Bonus Questions
What is the resistance of the $100$-watt light bulb?
What is the total resistance of the circuit?