When the universe hands us an equation, as we have already amply mentioned, it's usually a mess.
Today, using what we've learned in the previous sections, we begin to learn how to sort out the puzzle pieces nature hands to us.
Solve Equations with Variables and Constants on Both Sides
When a random equation walks up to us on the street and says "solve me," we devise a strategy for where to start.
Our first step in solving an equation is deciding which side of the equation the variables will go, and which side the constants will go.
That is, one side will be the "variable" side, and the other will be the "constant" side.
Our first two examples involve equations with constants on both sides.
Example: Constants on Both Sides
Solve the equation $7x + 8 = -13.$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{}\\\\ \displaystyle 7x+8&\displaystyle= -13 &\mbox{original equation}\\ \displaystyle 7x+8\color{magenta}{-8}&\displaystyle= -13\color{magenta}{-8}&\mbox{subtraction property of equality}\\ \displaystyle 7x&\displaystyle= -21&\mbox{simplify}\\ \displaystyle \frac{7x}{\color{magenta}{7}}&\displaystyle= \frac{-21}{\color{magenta}{7}}&\mbox{division property of equality}\\ \displaystyle x&\displaystyle=-3&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 7\color{magenta}{x}+8&\displaystyle= -13 &\mbox{original equation}\\ \displaystyle 7\color{magenta}{(-3)}+8&\displaystyle= -13 &\mbox{since $\color{magenta}{x=-3}$}\\ \displaystyle -21+8&\displaystyle= -13 &\mbox{}\\ \displaystyle -13&\displaystyle= -13 &\mbox{$\checkmark$}\\ \end{array} $$
Example: Constants on Both Sides
Solve the equation $8y-9=31.$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{}\\\\ \displaystyle 8y-9&\displaystyle= 31 &\mbox{original equation}\\ \displaystyle 8y-9\color{magenta}{+9}&\displaystyle= 31\color{magenta}{+9}&\mbox{addition property of equality}\\ \displaystyle 8y&\displaystyle= 40&\mbox{simplify}\\ \displaystyle \frac{8y}{\color{magenta}{8}}&\displaystyle= \frac{40}{\color{magenta}{8}}&\mbox{division property of equality}\\ \displaystyle y&\displaystyle=5&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 8\color{magenta}{y}-9&\displaystyle= 31 &\mbox{original equation}\\ \displaystyle 8\color{magenta}{(5)}-9&\displaystyle= 31&\mbox{since $\color{magenta}{y=5}$}\\ \displaystyle 40-9 &\displaystyle= 31 &\mbox{}\\ \displaystyle 31&\displaystyle=31 &\mbox{$\checkmark$}\\ \end{array} $$

Our next examples involve equations with variables on both sides.
Example: Variables on Both Sides
Solve the equation $9x = 8x - 6$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{}\\\\ \displaystyle 9x&\displaystyle= 8x -6 &\mbox{original equation}\\ \displaystyle 9x\color{magenta}{-8x}&\displaystyle= 8x -6 \color{magenta}{-8x}&\mbox{subtraction property}\\ \displaystyle x&\displaystyle= -6&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 9\color{magenta}{x}&\displaystyle= 8\color{magenta}{x} -6 &\mbox{}\\ \displaystyle 9\color{magenta}{(-6)}&\displaystyle= 8\color{magenta}{(-6)} -6&\mbox{}\\ \displaystyle -54&-48-6\displaystyle= -6&\mbox{}\\ \displaystyle -54&-54\displaystyle= -6&\mbox{$\checkmark$}\\ \end{array} $$
Example: Variables on Both Sides
Solve the equation $5y - 9 = 8y.$
This time, we will make the right side the variable side.
Solution
$$ \begin{array}{rll} \mbox{Constant Side}&\mbox{Variable Side}&\mbox{}\\\\ \displaystyle 5y-9&\displaystyle= 8y&\mbox{original equation}\\ \displaystyle 5y-9\color{magenta}{-5y}&\displaystyle= 8y \color{magenta}{-5y}&\mbox{subtraction property}\\ \displaystyle -9&\displaystyle= 3y&\mbox{simplify}\\ \displaystyle \frac{-9}{\color{magenta}{3}}&\displaystyle= \frac{3y}{\color{magenta}{3}}&\mbox{division property}\\ \displaystyle -3&\displaystyle= y&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 5\color{magenta}{y}-9&\displaystyle= 8\color{magenta}{y}&\mbox{original equation}\\ \displaystyle 5\color{magenta}{(-3)}-9&\displaystyle= 8\color{magenta}{(-3)}&\mbox{since $\color{magenta}{y=-3}$}\\ \displaystyle -15-9&\displaystyle=-24 \mbox{}\\ \displaystyle -24&\displaystyle=-24 \mbox{$\checkmark$}\\ \end{array} $$

We now tackle the case of when we have variables and constants on both sides.
Example: Variables and Constants on Both Sides
Solve the equation $7x + 5 = 6x + 2.$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{}\\\\ \displaystyle 7x + 5&\displaystyle= 6x+2&\mbox{original equation}\\ \displaystyle 7x+5\color{magenta}{-6x}&\displaystyle= 6x+2 \color{magenta}{-6x}&\mbox{subtraction property}\\ \displaystyle x+5&\displaystyle= 2&\mbox{simplify}\\ \displaystyle x+5\color{magenta}{-5}&\displaystyle= 2\color{magenta}{-5}&\mbox{subtraction property}\\ \displaystyle x&\displaystyle= -3&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 7\color{magenta}{x}+5&\displaystyle= 6\color{magenta}{x}+2&\mbox{original equation}\\ \displaystyle 7\color{magenta}{(-3)}+5&\displaystyle= 6\color{magenta}{(-3)}+2&\mbox{since $\color{magenta}{x=-3}$}\\ \displaystyle -21+5&\displaystyle=-18+2 &\mbox{}\\ \displaystyle -16&\displaystyle=-16 & \mbox{$\checkmark$}\\ \end{array} $$
Strategy for Solving Equations
Step 1: Choose which side will be the “variable” side—the other side will be the “constant” side.
Step 2: Collect the variable terms to the "variable" side of the equation, using the Addition or Subtraction Property of Equality.
Step 3: Collect all the constants to the "constant" side of the equation, using the Addition or Subtraction Property of Equality.
Step 4: Make the coefficient of the variable equal $1,$ using the Multiplication or Division Property of Equality.
Step 5: Check the solution by substituting it into the original equation.
Example: Variables and Constants on Both Sides
Solve the equation $7a - 3 = 13a + 7.$
Solution
$$ \begin{array}{rll} \mbox{Constant Side}&\mbox{Variable Side}&\mbox{$\color{blue}{\mbox{Step 1}}$}\\\\ \displaystyle 7a-3&\displaystyle= 13a+7&\mbox{original equation}\\ \displaystyle 7a-3\color{magenta}{-7a}&\displaystyle= 13a+7 \color{magenta}{-7a}&\mbox{subtraction property($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle -3&\displaystyle= 6a+7&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle -3\color{magenta}{-7}&\displaystyle= 6a+7\color{magenta}{-7}&\mbox{subtraction property ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle -10&\displaystyle= 6a&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{-10}{\color{magenta}{6}}&\displaystyle= \frac{6a}{\color{magenta}{6}}&\mbox{division property ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle -\frac{5}{3}&\displaystyle= a&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle 7\color{magenta}{a}-3&\displaystyle= 13\color{magenta}{a}+7&\mbox{original equation}\\ \displaystyle 7\color{magenta}{\left(-\frac{5}{3}\right)}-3&\displaystyle= 13\color{magenta}{\left(-\frac{5}{3}\right)}+7&\mbox{since $\displaystyle \color{magenta}{a=-\frac{5}{3}}$}\\ \displaystyle -\frac{35}{3}-\frac{9}{3}&\displaystyle=-\frac{65}{3}+\frac{21}{3} &\mbox{}\\ \displaystyle -\frac{44}{3}&\displaystyle=-\frac{44}{3} & \mbox{$\checkmark$}\\ \end{array} $$

Example: Variables and Constants on Both Sides
Solve the equation $\displaystyle \frac{5}{4}x +6 = \frac{1}{4}x -2.$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{$\color{blue}{\mbox{Step 1}}$}\\\\ \displaystyle \frac{5}{4}x +6&\displaystyle= \frac{1}{4}x -2&\mbox{original equation}\\ \displaystyle \frac{5}{4}x +6\color{magenta}{-\frac{1}{4}x}&\displaystyle= \frac{1}{4}x -2 \color{magenta}{-\frac{1}{4}x}&\mbox{subtraction property($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle x+6&\displaystyle= -2&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle x+6\color{magenta}{-6}&\displaystyle= -2\color{magenta}{-6}&\mbox{subtraction property ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle x&\displaystyle= -8&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle &\displaystyle &\mbox{$\color{blue}{\mbox{Step 4}}$ not necessary}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle \frac{5}{4}\color{magenta}{x}+6&\displaystyle= \frac{1}{4}\color{magenta}{x}-2&\mbox{original equation}\\ \displaystyle \frac{5}{4}\color{magenta}{(-8)}+6&\displaystyle= \frac{1}{4}\color{magenta}{(-8)}-2&\mbox{since $\displaystyle \color{magenta}{x=-8}$}\\ \displaystyle -\frac{40}{4}+6&\displaystyle=-\frac{8}{4}-2 &\mbox{}\\ \displaystyle -10+6&\displaystyle=-2-2 & \mbox{}\\ \displaystyle -4&\displaystyle=-4 & \mbox{$\checkmark$}\\ \end{array} $$
Example: Variables and Constants on Both Sides
Solve the equation $7.8x + 4 = 5.4x - 8.$
Solution
$$ \begin{array}{rll} \mbox{Variable Side}&\mbox{Constant Side}&\mbox{$\color{blue}{\mbox{Step 1}}$}\\\\ \displaystyle 7.8x +4&\displaystyle= 5.4x-8&\mbox{original equation}\\ \displaystyle 7.8x +4\color{magenta}{-5.4x}&\displaystyle= 5.4x-8\color{magenta}{-5.4x}&\mbox{subtraction property($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 2.4x+4&\displaystyle= -8&\mbox{simplify ($\color{blue}{\mbox{Step 2}}$)}\\ \displaystyle 2.4x+4\color{magenta}{-4}&\displaystyle= -8\color{magenta}{-4}&\mbox{subtraction property ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle 2.4x&\displaystyle= -12&\mbox{simplify ($\color{blue}{\mbox{Step 3}}$)}\\ \displaystyle \frac{2.4x}{\color{magenta}{2.4}}&\displaystyle \frac{-12}{2.4}&\mbox{division property ($\color{blue}{\mbox{Step 4}}$)}\\ \displaystyle x&\displaystyle= -\frac{120}{24}=-5&\mbox{simplify ($\color{blue}{\mbox{Step 4}}$)}\\ \end{array} $$ Check ($\color{blue}{\mbox{Step 5}}$) $$ \begin{array}{rll} \displaystyle 7.8\color{magenta}{x}+4&\displaystyle= 5.4\color{magenta}{x}-8&\mbox{original equation}\\ \displaystyle 7.8\color{magenta}{(-5)}+4&\displaystyle= 5.4\color{magenta}{(-5)}-8&\mbox{since $\displaystyle \color{magenta}{x=-5}$}\\ \displaystyle -39+4&\displaystyle=-27-8 &\mbox{}\\ \displaystyle -35&\displaystyle=-35 & \mbox{$\checkmark$}\\ \end{array} $$
Whadda ya say we lighten things up and talk about declining manatee populations?
Question
Is there a relationship between manatee deaths caused by boats and boat registrations in Florida?

The Data
The table below lists the number of Florida boat registrations and manatee deaths from 1977 to 2009. $$ \begin{array}{ccc} \hline \mbox{Year} & \mbox{Boat Registrations} & \mbox{Manatee Deaths}\\\hline 1977 & 447 & 13\\ \hline 1978 & 460 & 21\\ \hline 1979 & 481 & 24\\ \hline 1980 & 498 & 16\\ \hline 1981 & 513 & 24\\ \hline 1982 & 512 & 20\\ \hline 1983 & 526 & 15\\ \hline 1984 & 559 & 34\\ \hline 1985 & 585 & 33\\ \hline 1986 & 614 & 33\\ \hline 1987 & 645 & 39\\ \hline 1988 & 675 & 43\\ \hline 1989 & 711 & 50\\ \hline 1990 & 719 & 47\\ \hline 1991 & 681 & 53\\ \hline 1992 & 679 & 38\\ \hline 1993 & 678 & 35\\ \hline 1994 & 696 & 49\\ \hline 1995 & 713 & 42\\ \hline 1996 & 732 & 60\\ \hline 1997 & 755 & 54\\ \hline 1998 & 809 & 66\\ \hline 1999 & 830 & 82\\ \hline 2000 & 880 & 78\\ \hline 2001 & 944 & 81\\ \hline 2002 & 962 & 95\\ \hline 2003 & 978 & 73\\ \hline 2004 & 983 & 69\\ \hline 2005 & 1010 & 79\\ \hline 2006 & 1024 & 92\\ \hline 2007 & 1027 & 73\\ \hline 2008 & 1010 & 90\\ \hline 2009 & 982 & 97\\ \hline \end{array} $$
The Data
Below is a scatterplot of manatee deaths versus the number of boat registrations in Florida. Each point represents a particular year.
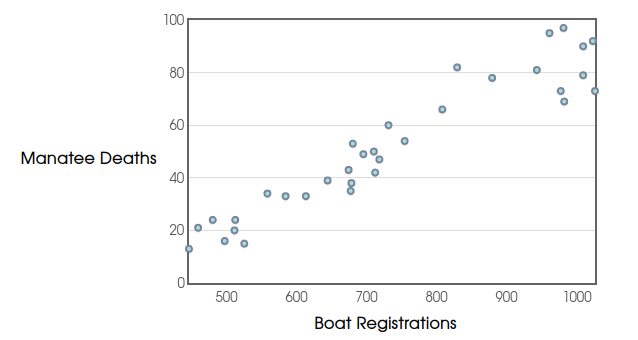
We are now going to model this data with a straight line....
The Model
Below is the manatee death versus boat registration data with a line which models the overall trend.
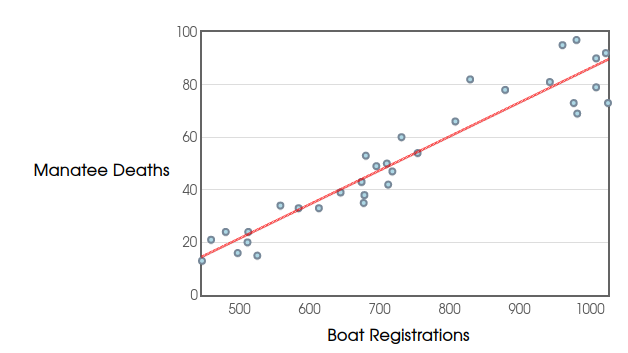
The equation for this "line-of-best-fit" for the manatee data is $D=0.129R-43.172$.
Thus, if we know in advance the number of boat registrations $R$ for the year, we can roughly predict how many manatee deaths $D$ will occur in that year.
Questions
Suppose you're a marine biologist who studies manatee populations.
Using the model $D=0.129 R-43.172,$ we can answer the following questions.
(a) Suppose we know that there are $823$ boat registrations this year. About how many manatees can we expect will be killed by boats?
(b) Suppose $60$ manatees were killed by boats last year, estimate how many boat registrations there were.
Solutions
(a) Since there were $823$ boat registrations last year, we may write $R=823.$ Then, $$ D=0.129 R-43.172=0.0.129(823)-43.172=62.995 $$ Thus, we can expect about $63$ manatee deaths this year.
(b) Since $60$ manatees were killed, we may write $D=60.$ Then, $$ 60=0.129 R-43.172. $$ Thus, we need to solve for $R.$ $$ \begin{array}{rll} \mbox{Constant Side}&\mbox{Variable Side}&\mbox{}\\\\ \displaystyle 60&\displaystyle= 0.129 R-43.172&\mbox{original equation}\\ \displaystyle 60\color{magenta}{+43.172}&\displaystyle= 0.129 R-43.172 \color{magenta}{+43.172}&\mbox{addition property}\\ \displaystyle 103.172&\displaystyle= 0.129 R&\mbox{simplify}\\ \displaystyle \frac{103.172}{\color{magenta}{0.129}}&\displaystyle= \frac{0.129 R}{\color{magenta}{0.129}}&\mbox{division property}\\ \displaystyle 799.782945736 &\displaystyle= R&\mbox{simplify}\\ \end{array} $$ Check $$ \begin{array}{rll} \displaystyle 60&\displaystyle= 0.129\color{magenta}{R}-43.172&\mbox{original equation}\\ \displaystyle 60&\displaystyle= 0.129\color{magenta}{(799.782945736)}-43.172&\mbox{since $\displaystyle \color{magenta}{R=799.782945736}$}\\ \displaystyle 60&\displaystyle=60 & \mbox{$\checkmark$}\\ \end{array} $$ So, we estimate that there were about $800$ boat registrations last year.
Translation Practice
Jovani has $150$ feet of fencing to make a rectangular garden in his backyard.
He wants the length to be $15$ feet more than the width.
Find the width of the fence.
Solution
Step 1. Read and understand the problem.
Step 2. Identify what we want.
We want to find the width of the rectangular garden.
Step 3. Name what we want.
Call the width $w.$ We will also call the length of the garden $\ell$ since this is mentioned in the problem.
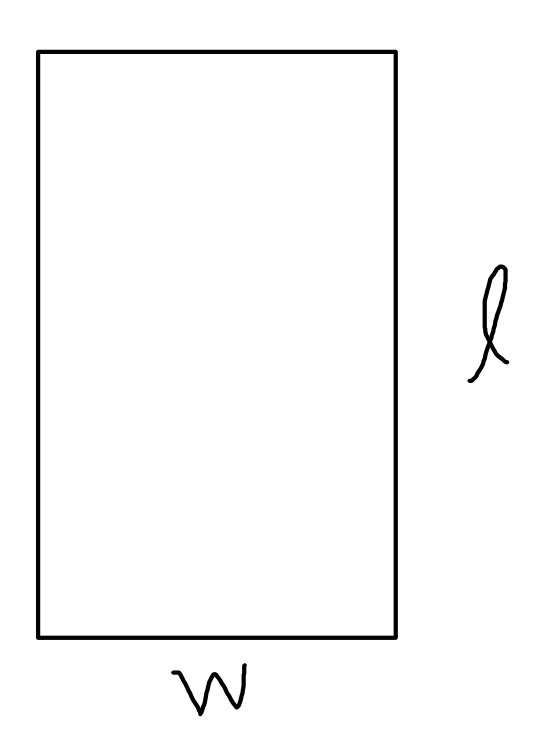
Step 4. Translate.
English: "He wants the length to be $15$ feet more than the width."
Algebra: $\ell=w+15$
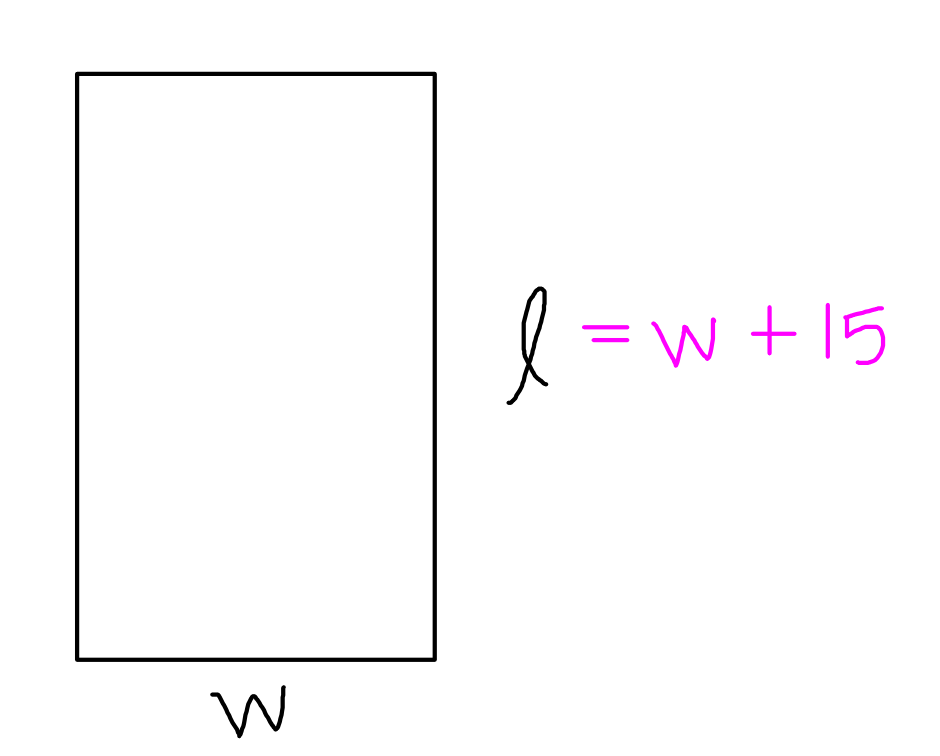
We are also given another important piece of information.
English: "Jovani has $150$ feet of fencing."
Algebra: $w+(w+15)+w+(w+15)=\mbox{perimeter}=150$
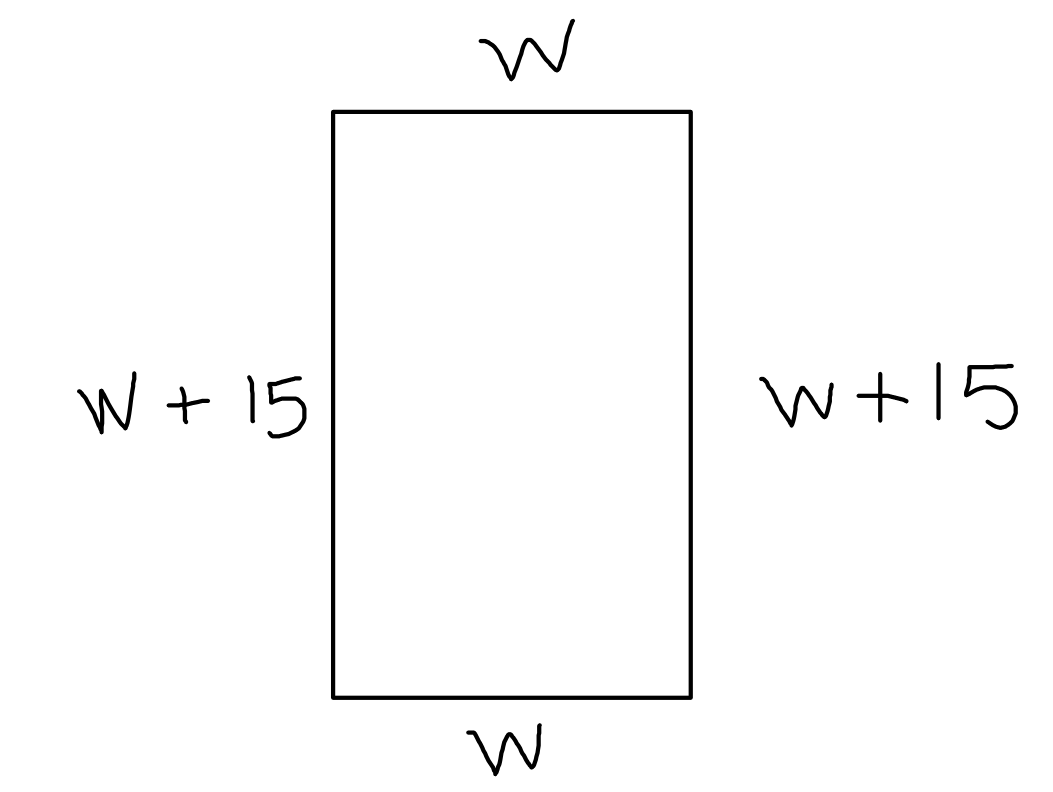
The equation to solve is $w+(w+15)+w+(w+15)=150$
Step 5. Solve.
$$ \begin{array}{rll} \displaystyle w+(w+15)+w+(w+15) &\displaystyle= 150 &\mbox{original equation}\\ \displaystyle w+w+15+w+w+15 &\displaystyle= 150 &\mbox{simplify}\\ \displaystyle 4w+30 &\displaystyle= 150 &\mbox{simplify}\\ \displaystyle 4w+30\color{magenta}{-30} &\displaystyle= 150\color{magenta}{-30} &\mbox{subtraction property}\\ \displaystyle 4w &\displaystyle= 120&\mbox{simplify}\\ \displaystyle \frac{4w}{\color{magenta}{4}} &\displaystyle= \frac{120}{\color{magenta}{4}}&\mbox{division property}\\ \displaystyle w &\displaystyle= 30&\mbox{simplify}\\ \end{array} $$
Step 6. Check.
For $w=\color{magenta}{30},$ we have the following.
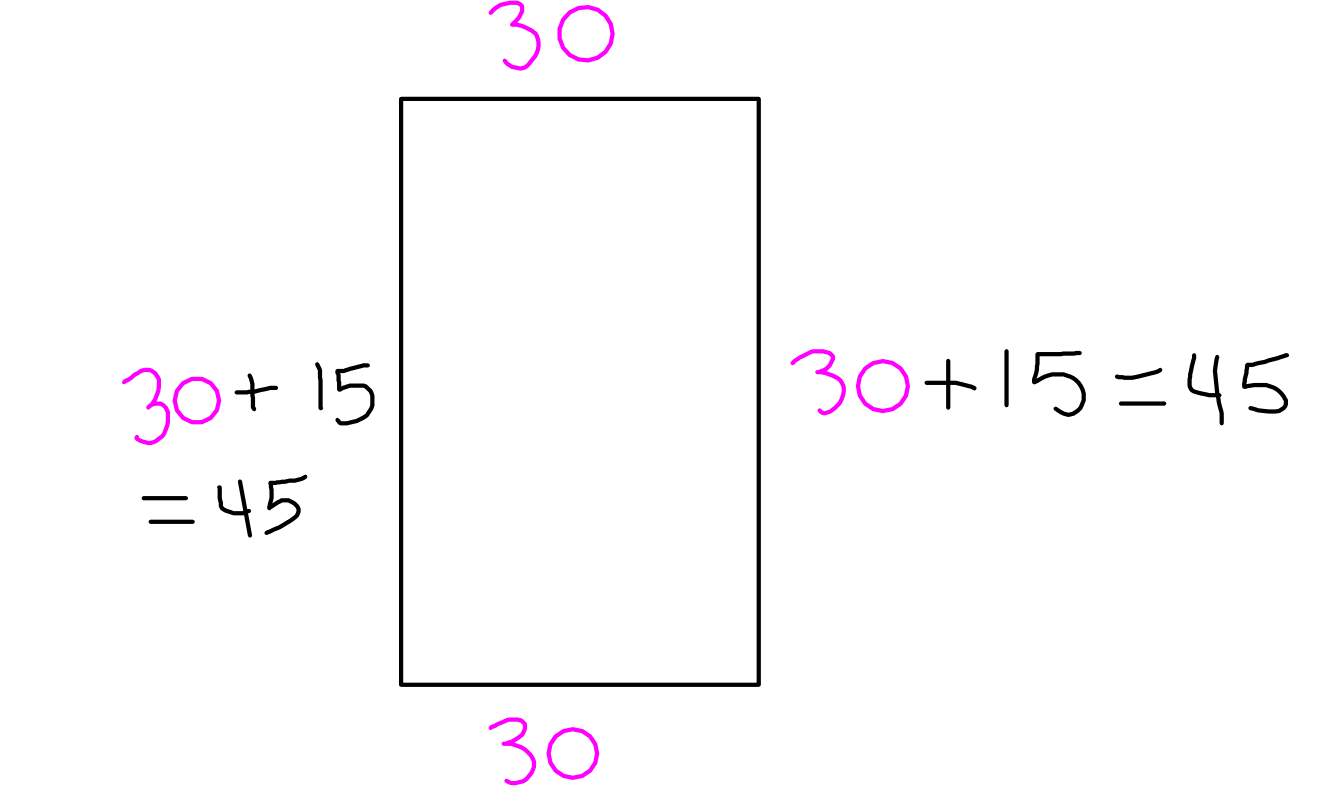
The length, $45,$ is $15$ more than the width, $30.$ $\checkmark$

The total amount of fencing is $\color{magenta}{30}+45+\color{magenta}{30}+45= 150.$ $\checkmark$

Step 7. State the answer as a complete sentence.
The width of the fence is $30$ feet.
