Last time we dealt with addition and subtraction separately.
Today we deal with multiplication and division.
An Illustration
Suppose we need to solve the equation $2x=6.$
We can imagine the $x$ as an envelope holding an unknown number of gold coins.
When we double the envelope's contents, we get $6.$
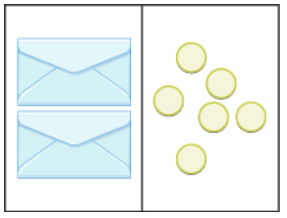
An Illustration
Breaking up both the left hand side and the right hand side into two equally-sized groups, we have the following.
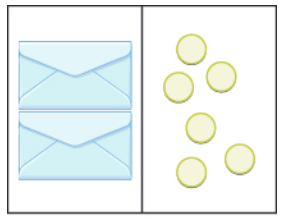
From the illustration, it is apparent that each envelope contains $3$ coins.
Quick Question: Breaking up a group into smaller groups all of equal size reminds us of what process?
The Symbolic Version
$$ \begin{array}{rll} \displaystyle 2x&=\displaystyle 6 &\mbox{the original equation}\\ \displaystyle \frac{2x}{\color{magenta}{2}}&=\displaystyle \frac{6}{\color{magenta}{2}} &\mbox{divide both sides by $2$}\\ \displaystyle x&=\displaystyle 3 &\mbox{simplify}\\ \end{array} $$
The above illustrates a general principle when finding solutions to equations...
The Division Property of Equality
For any numbers $a,$ $b,$ and $c\neq 0,$ if $a = b,$ then $$\frac{a}{c} = \frac{b}{c}$$ When you divide by the same quantity on both sides of an equation, you still have equality.
Example
Solve the equation $5x = -27.$
Solution
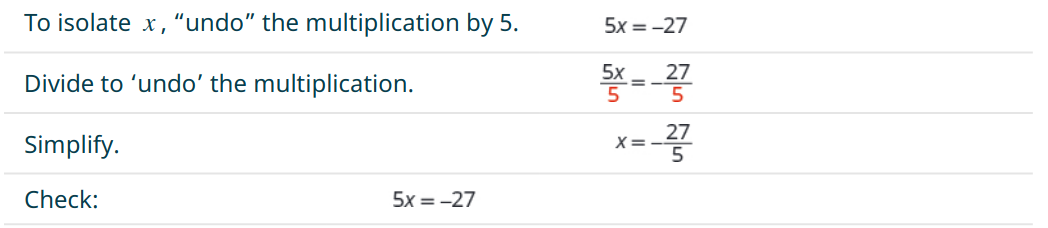

The Multiplication Property of Equality
For any numbers $a,$ $b,$ and $c,$ if $a = b,$ then $$ac =bc$$ When you divide by the same quantity on both sides of an equation, you still have equality.
Example
Solve the equation $\displaystyle \frac{y}{-7}=-14.$
Solution

Examples
Solve the equations and check your solutions.
(a) $-n=9$
(b) $\displaystyle \frac{3}{4}x=12$
(c) $\displaystyle \frac{8}{15}=-\frac{4}{5}x$
(d) $14 - 23 = 12y - 4y - 5y$
(e) $-4(a - 3) - 7 = 25$
Solutions
(a) 
(b)
(c)
(d)
(e)

(b)

(c)

(d)

(e)

Arithmetic Operations Preserve Equality

Example
Translate and solve: The quotient of $y$ and $-4$ is $68.$
Solution

Number Problems
Number problems are truly nerdy and at this level are not super useful.
The basic skill these problems develop is translating verbal statements into mathematical statements.
Example: A Typical Algebra-Level Number Problem
The product of two consecutive odd integers is $255.$
Letting $x$ is the smallest of the integers,
(a) write an equation in terms of $x$ that describes the situation, and
(b) find all such pairs of integers.
Example: A Data-Security Number Problem
Find two large prime numbers $p$ and $q$ which do not divide a number $a$ (which represents an encrypted message).
Then find two numbers $e$ and $d$ such that the remainder is $1$ when dividing their product by $(p-1)(q-1).$
While this is also a nerdy number problem, you have its solution to thank for helping keeping your online communications secure.
Recall: Rough Guide for Solving Word Problems
Step 1: Read the problem. Make sure all the words and ideas are understood.
Step 2: Identify what we are looking for.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
Step 4: Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
Step 5: Solve the equation using good algebra techniques.
Step 6: Check the answer in the problem and make sure it makes sense.
Step 7: Answer the question with a complete sentence.
Example
Andreas bought a used car for $\mbox{\$12,000.}$
Because the car was $4$ years old, its price was $\displaystyle \frac{3}{4}$ of the original price, when the car was new. What was the original price of the car?
Solution
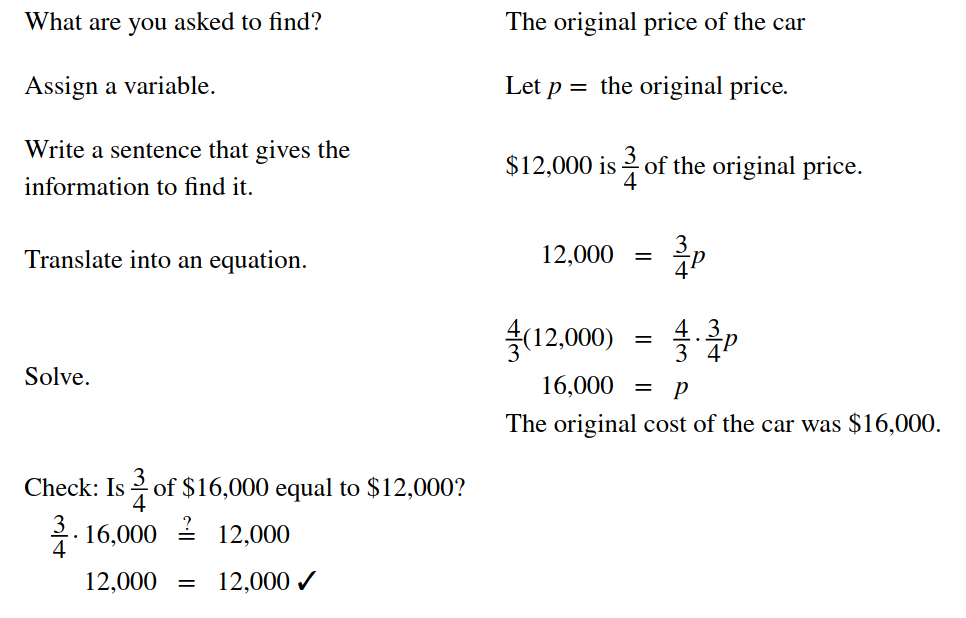
It may come as no surprise that some laws of nature have complex mathematical descriptions.
On the other hand, some have very simple descriptions.
Story Time!
Between 1825 and 1826, Georg Ohm observed through experimentation that the current flowing though an electric circuit is the quotient of the voltage and resistance.
The above is known as Ohm's Law.
Ohm's work, Die galvanische Kette, mathematisch bearbeitet (The Galvanic Circuit Investigated Mathematically), published in 1827, is one of the earliest scientific treatments of electrical phenomena.


Translation Practice
Translate the following statement into algebraic language.
"The current flowing though an electric circuit is the quotient of the voltage and resistance."
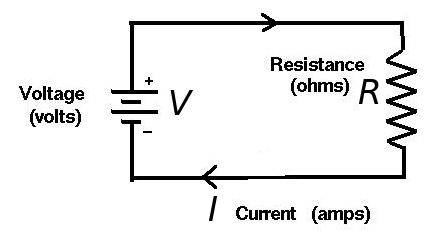
An Honest-to-Goodness Application
In a simple circuit like the one below, the current $I$ in amperes, the resistance $R$ in ohms, and the voltage $V$ in volts, are related by Ohm's Law. $$ I=\frac{V}{R} $$

Example
The resistance of an incandescent $60$ watt light bulb is $240$ ohms and draws a current of $0.5$ amperes.
What is the the voltage in the circuit?


Solution
From the problem situation we know that $R=240$ ohms and $I=0.5$ amps.
Then, $$ \begin{array}{rll} \displaystyle I&\displaystyle=\frac{V}{R} &\mbox{Ohm's Law}\\ \displaystyle 0.5&\displaystyle=\frac{V}{240} &\mbox{ since $R=240$ ohms and $I=0.5$}\\ \displaystyle \color{magenta}{240}\cdot 0.5&\displaystyle=\color{magenta}{240} \cdot \frac{V}{240} &\mbox{ multiply both sides by 240}\\ \displaystyle 120 &\displaystyle= V&\mbox{simplify}\\ \end{array} $$ Check
$$ \begin{array}{lll} \displaystyle 0.5&\displaystyle=\frac{\color{magenta}{V}}{240} &\mbox{}\\ \displaystyle 0.5&\displaystyle=\frac{\color{magenta}{120}}{240} &\mbox{since $V=120$ volts}\\ \displaystyle 0.5&\displaystyle=\frac{1}{2} &\mbox{simplifying}\\ \displaystyle 0.5&\displaystyle=0.5 &\mbox{$\checkmark$}\\ \end{array} $$
Thus, the voltage across the circuit is $120$ volts.