We have already seen the beginnings of the subject of algebra in Chapter 1.
Today, we get started in earnest with solving equations.
But before we do, let's recall the general idea of algebra...
Equations
An equation is a statement that two quantities are equal.
For example, $2=2$ is an equation which happens to be a true statement.
$2=1$ is also an equation which happens to be a false statement.
These are the simplest examples though.
When the universe hands us puzzle pieces to an incomplete picture, it is up to us to fill the rest in.

Solving Equations
Let's now consider a different kind of equation which involves an unknown quantity $x.$ $$2x=4$$ To solve this equation is to find a value of $x$ which makes a true statement.

And I bet some of you know already which $x$ would make the statement true!
Solving Equations
Of course the kinds of equations the universe throws at us usually aren't as elementary as the one above. For example, can you find a value of $x$ which makes the following statement true? $$4x - 2 = 2x + 1$$ This is a bit less obvious than the previous equation.

One of the main goals of this chapter is to be able to recover value(s) of $x$ which make statements like the above true.
Example
Show that $\displaystyle x=\frac{3}{2}$ is a solution to the equation $$4x - 2 = 2x + 1$$

Solution
For the left hand side, $$ \begin{array}{lll} \displaystyle 4x-2&= \displaystyle 4\left(\frac{3}{2}\right)-2 &\mbox{ since $\displaystyle x=\frac{3}{2}$}\\ &= \displaystyle 6-2 &\mbox{}\\ &= \displaystyle 4 &\mbox{}\\ \end{array} $$ For the right hand side, $$ \begin{array}{lll} \displaystyle 2x + 1&=\displaystyle 2\left(\frac{3}{2}\right)+1 &\mbox{ since $\displaystyle x=\frac{3}{2}$}\\ &= \displaystyle 3+1 &\mbox{}\\ &= \displaystyle 4 &\mbox{}\\ \end{array} $$
Since both sides evaluate the same, $\displaystyle x=\frac{3}{2}$ solves $4x - 2 = 2x + 1$
The First Layer of the Onion
Today, we begin peeling away the layers by learning how to solve equations involving only addition and subtraction.
An Illustration
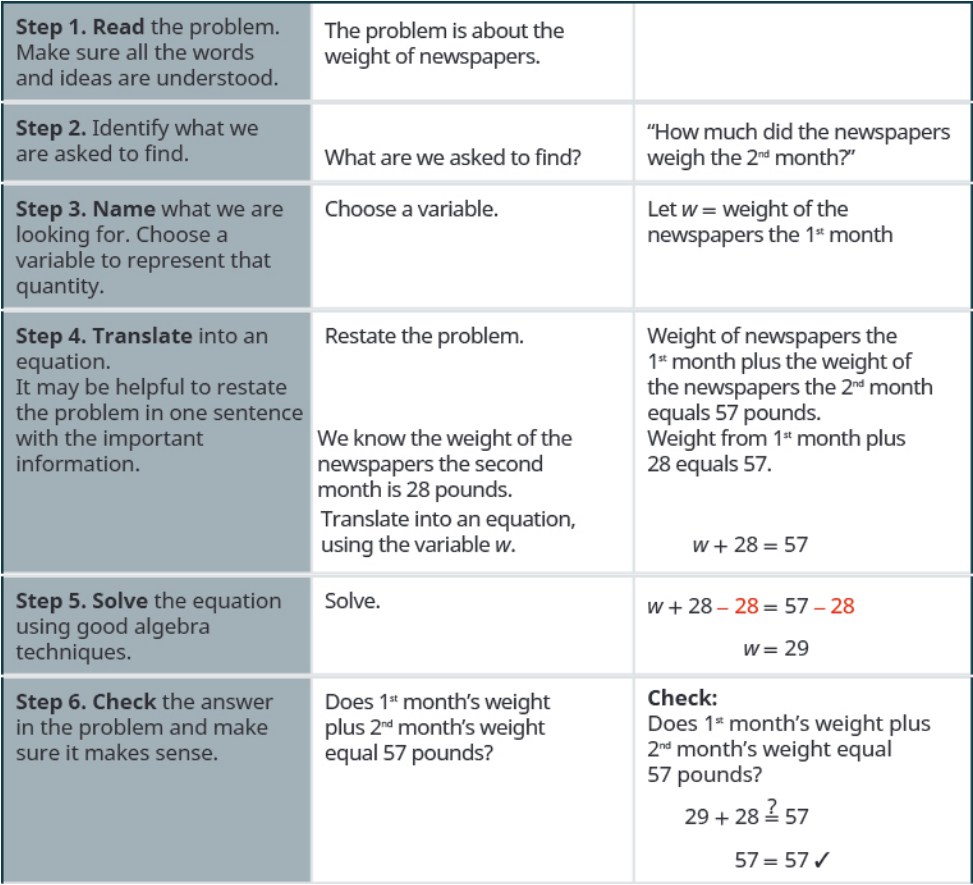
Suppose we need to solve the equation $x+3=8.$
We can imagine the $x$ as an envelope holding an unknown number of gold coins.
The left and right side represent the same quantity. The question is: how many gold coins are in the envelope?
The number of gold coins increased by $3$ gives us a total of $8$ coins.
An Illustration
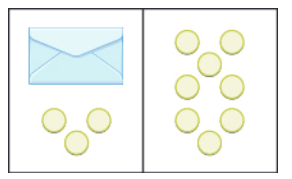
Since both sides represent the same amount, we can remove $3$ coins from both sides and still have a true statement.
That is, the amount on the left is still the same amount on the right after removing $3$ coins from both sides.
An Illustration
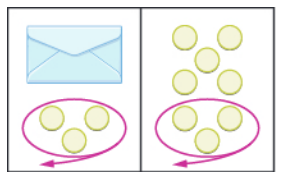
After removing the coins, we have the following picture.
What equation is represented by this picture?
An Illustration
$x=5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$


Let's verify that $x=5$ solves the original equation.
The Symbolic Version
$$ \begin{array}{rll} \displaystyle x+3&=\displaystyle 8 &\mbox{the original equation}\\ \displaystyle x+3\color{magenta}{-3}&=\displaystyle 8 \color{magenta}{-3} &\mbox{subtract $3$ from both sides}\\ \displaystyle x&=\displaystyle 5 &\mbox{simplify}\\ \end{array} $$
The above illustrates a general principle when finding solutions to equations...
The Subtraction Property of Equality
For any numbers $a,$ $b,$ and $c,$ If $a = b,$ then $$a - c = b - c$$ When you subtract the same quantity from both sides of an equation, you still have equality.
Example
Solve the equation $y+37=-13$
Solution
$$ \begin{array}{rll} \displaystyle y+37&=\displaystyle -13 &\mbox{the original equation}\\ \displaystyle y+37\color{magenta}{-37}&=\displaystyle -13 \color{magenta}{-37} &\mbox{subtract $37$ from both sides}\\ \displaystyle y&=\displaystyle -50 &\mbox{simplify}\\ \end{array} $$
Check
For the left hand side of original equation, $$ \begin{array}{lll} \displaystyle y+37&= \displaystyle -50+37 &\mbox{ since $\displaystyle y=-50$}\\ &= \displaystyle -13 &\mbox{}\\ \end{array} $$ which is the same as the right-hand side of original equation.
We may also add the same quantity to both sides...
The Addition Property of Equality
For any numbers $a,$ $b,$ and $c,$ If $a = b,$ then $$a + c = b + c$$ When you add the same quantity to both sides of an equation, you still have equality.
Example
Solve the equation $a-28=-37$
Solution
$$ \begin{array}{rll} \displaystyle a-28&=\displaystyle -37 &\mbox{the original equation}\\ \displaystyle a-28\color{magenta}{+28}&=\displaystyle -37 \color{magenta}{+28} &\mbox{add $28$ to both sides}\\ \displaystyle a&=\displaystyle -9 &\mbox{simplify}\\ \end{array} $$
Check
For the left hand side of the original equation, $$ \begin{array}{lll} \displaystyle a-28&= \displaystyle -9-28 &\mbox{ since $\displaystyle a=-9$}\\ &= \displaystyle -37 &\mbox{}\\ \end{array} $$ which is the same as the right-hand side of the original equation.
Example
Solve the equation $\displaystyle x-\frac{5}{8}=\frac{3}{4}.$
Solution
$$ \begin{array}{rll} \displaystyle x-\frac{5}{8}&=\displaystyle \frac{3}{4} &\mbox{the original equation}\\ \displaystyle x-\frac{5}{8}\color{magenta}{+\frac{5}{8}}&=\displaystyle \frac{3}{4} \color{magenta}{+\frac{5}{8}} &\mbox{add $\displaystyle \frac{5}{8}$ to both sides}\\ \displaystyle x&=\displaystyle \frac{11}{8} &\mbox{simplify}\\ \end{array} $$
Check
For the left hand side of the original equation, $$ \begin{array}{lll} \displaystyle x-\frac{5}{8}&= \displaystyle \frac{11}{8}-\frac{5}{8} &\mbox{since $\displaystyle x=\frac{11}{8}$}\\ &= \displaystyle \frac{6}{8} &\mbox{after adding}\\ &= \displaystyle \frac{3}{4} &\mbox{after simplifying}\\ \end{array} $$ which is the same as the right-hand side of the original equation.
Example
Solve the equation $\displaystyle n - 0.63 = -4.2.$
Solution
$$ \begin{array}{rll} \displaystyle n - 0.63 &=\displaystyle -4.2 &\mbox{the original equation}\\ \displaystyle n - 0.63\color{magenta}{+0.63}&=\displaystyle -4.2\color{magenta}{+0.63} &\mbox{add $0.62$ to both sides}\\ \displaystyle n&=\displaystyle -3.57 &\mbox{simplify}\\ \end{array} $$
Check
For the left hand side of the original equation, $$ \begin{array}{lll} \displaystyle n - 0.63&= \displaystyle -3.57-0.63 &\mbox{ since $\displaystyle n=-3.57$}\\ &= \displaystyle -4.2 &\mbox{after simplifying}\\ \end{array} $$ which is the same as the right-hand side of the original equation.
Equations Requiring Simplification
Before we can even begin working on both sides of an equals sign, equations more often than not require that we simplify expressions first on one or both sides.
Example
Solve the equation $\displaystyle 9x - 5 - 8x - 6 = 7.$
Solution
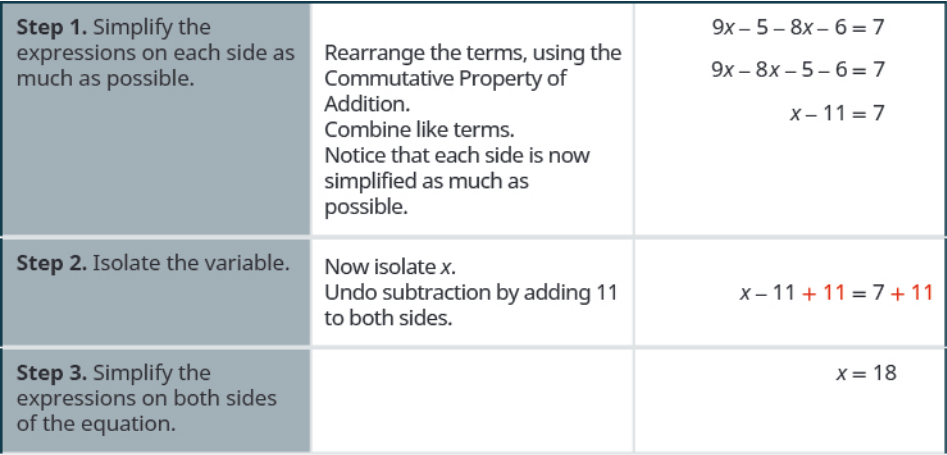
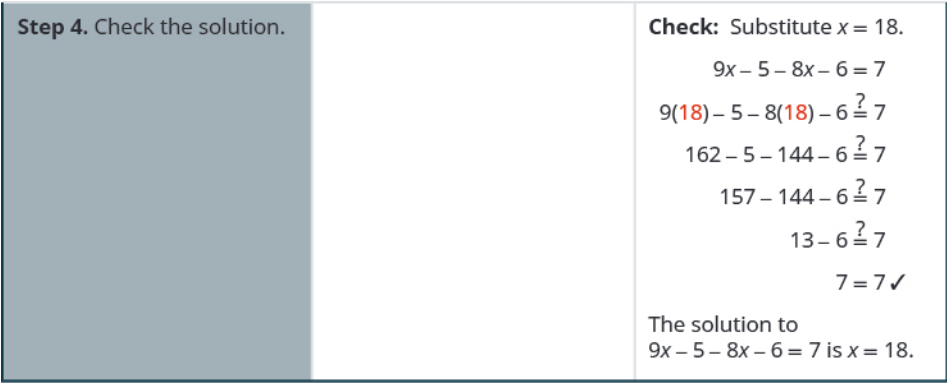
Example
Solve the equation $\displaystyle 5(n - 4) - 4n = -8.$
Solution
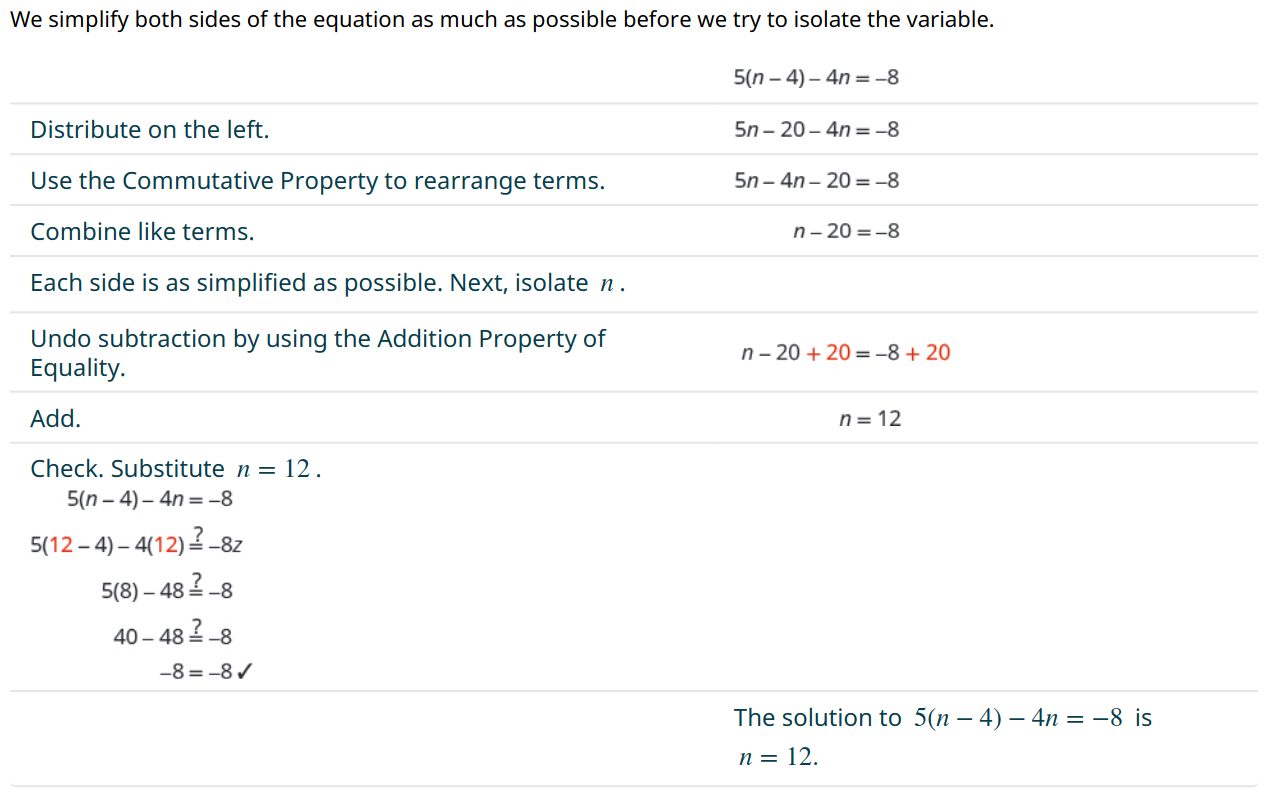
Example
Solve the equation $$\displaystyle 3(2y - 1) - 5y = 2(y+1)-2(y+3)$$
Solution

Recall: Translating from English to Algebra

Example
Translate and solve: Eleven more than $x$ is equal to $54.$
Solution

Applications of Equations
Fact: Applied problems in an algebra class are more often silly than useful.
However...
Such problems are the building blocks of more complex and realistic models of our world.
To learn any skill requires learning rudiments which can assembled into something useful or beautiful.
For example...
An Analogy
A great football player must do many things to achieve greatness on the field.
One of these is strength training.
Will lifting weights alone make a football player great? Is getting strong the the ultimate goal?
Is being strong a basic requirement for being a great football player?
More Analogies
A classical pianist must first learn to read music, practice scales, and train the ear.
Learning a new language requires learning new symbols, vocabulary, and grammar.
To learn how to draw, one must learn perspective, anatomies of living things, and understand the nature of light.
None of the blue items above constitute the practice of their respective disciplines, yet these disciplines cannot be practiced without these skills.
An Analogy
In the same way, to get good at applying mathematical ideas as models of the real world, we must must begin with idealizations and simple situations.
Most of application problems we do in this class will resemble the grunt work of getting good at a worthwhile skill: lifting weights, practicing scales, and learning grammar.
However, there will be some situations when we catch a glimpse of how we may begin applying these ideas in a more realistic way.

Rough Guide for Solving Word Problems
Step 1: Read the problem. Make sure all the words and ideas are understood.
Step 2: Identify what we are looking for.
Step 3: Name what we are looking for. Choose a variable to represent that quantity.
Step 4: Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
Step 5: Solve the equation using good algebra techniques.
Step 6: Check the answer in the problem and make sure it makes sense.
Step 7: Answer the question with a complete sentence.
Example
The MacIntyre family recycled newspapers for two months.
The two months of newspapers weighed a total of $57$ pounds.
The second month, the newspapers weighed $28$ pounds.
How much did the newspapers weigh the first month?

Solution