The real numbers exhibit many patterns and properties.
Today, we learn about the most important of these in order to do algebra.
Property #1: Addition and Multiplication are Commutative
For any two real numbers $a$ and $b,$ addition and multiplication are commutative. That is, $$ a+b=b+a \,\,\,\,\,\,\,\, \mbox { and } \,\,\,\,\,\,\,\, ab=ba $$
Example: $3+(-5)$ is the same as $-5+3$.
Example: $3\cdot(-5)$ is the same as $-5\cdot 3$
Real World Application: You use the commutative law of addition almost every day. How can that be?! D:
Seeing that Multiplication is Commutative
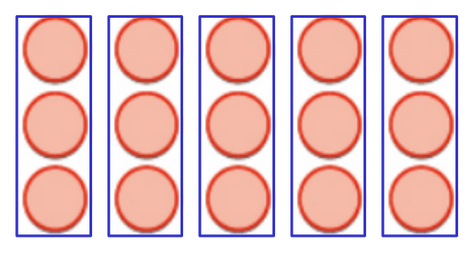
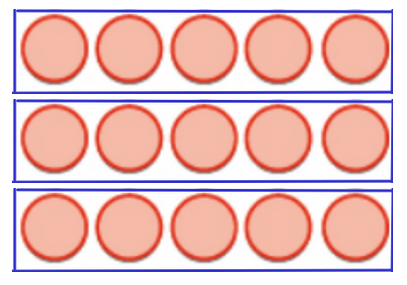
$5\cdot 3=3+3+3+3+3=15 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3 \cdot 5=5+5+5=15$
What Do You Think?
Are subtraction or division commutative?
Answer
Subtraction is not commutative.
Since $7-3=4,$ and $3-7=-4,$ we see that $$ 7-3\neq 3-7 $$
Division is also not commutative.
Since $3\div 1=3,$ and $1\div 3=\displaystyle \frac{1}{3},$ we see that $$ 3 \div 1 \neq 1\div 3 $$
Property #2: Addition and Multiplication are Associative
For any two real numbers $a,$ $b,$ and $c,$ addition and multiplication are associative. That is, $$ (a+b)+c=a+(b+c) \,\,\,\,\,\,\,\, \mbox { and } \,\,\,\,\,\,\,\, (ab)c=a(bc) $$
Example: $(7+8)+2=15+2=17$ and $7+(8+2)=7+10=17.$ So, $$(7+8)+2=7+(8+2).$$
Example: $(7\cdot 8)\cdot 2=56\cdot 2=112$ and $7\cdot (8\cdot 2)=7\cdot 16=112.$ So, $$(7\cdot 8)\cdot 2=7\cdot (8\cdot 2).$$
What Do You Think?
Are subtraction or division associative?
Answer
Subtraction is not associative.
Since $(7-8)-2=1-1-2=-3$ and $7-(8-2)=7-6=1,$ we see that $$ (7-8)-2\neq 7-(8-2) $$
Division is also not associative.
Since $\displaystyle (7\div 8)\div 2=\frac{7}{8}\div 2=\frac{7}{8}\cdot \frac{1}{2}=\frac{7}{16}$ and $\displaystyle 7\div (8\div 2)=7\div 4=\frac{7}{4},$ we see that $$ (7\div 8)\div 2\neq 7\div (8\div 2) $$
Simplifying Algebraic Expressions
The commutativity and the associativity of both addition and multiplication allows us to massage expressions into other forms which are more convenient to the kinds of shenanigans we'd like to pull.
Example: Simplify $18p + 6q + 15p + 5q$
Example: Simplify $6(3x)$
Solutions
$$ \begin{array}{lll} \displaystyle 18p + 6q + 15p + 5q &= \displaystyle 18p + 15p + 5q + 6q&\mbox{by the commutative property of addition}\\ &= \displaystyle (18p + 15p) + (5q + 6q)&\mbox{by the associative property of addition}\\ &= \displaystyle 33p + 11q&\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle 6(3x)&= \displaystyle (6\cdot 3)x&\mbox{by the associative property of multiplication}\\ &= \displaystyle 18x&\\ \end{array} $$
Property #3: Additive and Multiplicative Identities
$0$ is the additive identity since for any number $a$ $$ a+0=0+a=a $$ That is, adding $0$ to an expression doesn't change its value.
$1$ is the multiplicative identity since for any number $a$ $$ a\cdot 1=1\cdot a=a $$ That is, multiplying an expression by $1$ doesn't change its value.
Property #4: Additive and Multiplicative Inverses
For any real number $a,$ $$ a+(-a)=(-a)+a=0 $$ $a$ and $-a$ are called additive inverses.
For any real number $a$ except 0 (we'll have more to day about this later), $$ a\cdot \frac{1}{a}=\frac{1}{a}\cdot a =1 $$ $a$ and $\displaystyle \frac{1}{a}$ are called multiplicative inverses.
Examples
Fill in the blank.
$5+$ ______ $=0$
$-6+$ ______ $=0$
$2\cdot$ ______ $=1$
$\displaystyle \frac{2}{3}\cdot$ ______ $=1$
Solutions
Fill in the blank.
$5+\color{blue}{(-5)}=0$
$-6+\color{blue}{6}=0$
$\displaystyle 2\cdot\color{blue}{\frac{1}{2}}=1$
$\displaystyle \frac{2}{3}\cdot\color{blue}{\frac{3}{2}}=1$
Examples
Find the additive inverses of
ⓐ $\displaystyle \frac{5}{8}$
ⓑ $0.6$
ⓒ $-8$
ⓓ $\displaystyle -\frac{4}{3}$
Solution
ⓐ The additive inverse of $\displaystyle \frac{5}{8}$ is $-\displaystyle \frac{5}{8}.$
ⓑ The additive inverse of $0.6$ is $-0.6.$
ⓒ The additive inverse of $-8$ is $8.$
ⓓ The additive inverse of $\displaystyle -\frac{4}{3}$ is $\displaystyle \frac{4}{3}.$
Examples
Find the multiplicative inverses of
ⓐ $\displaystyle 9$
ⓑ $\displaystyle -\frac{1}{9}$
ⓒ $\displaystyle 0.9$
Solution
ⓐ The multiplicative inverse of $\displaystyle 9$ is $\displaystyle \frac{1}{9}.$
ⓑ The multiplicative inverse of $\displaystyle -\frac{1}{9}$ is $\displaystyle -9$
ⓒ The multiplicative inverse of $\displaystyle 0.9=\frac{9}{10}$ is $\displaystyle \frac{10}{9}$
There is a Number...
There is a number, which lives at the center of the universe.
It is the most powerful number, capable of unravelling the fabric of the universe.
With a single multiplication, it can devour any other number, rational, or irrational.
When added, is can hide in the inky shadows, undetected.
Indeed, it is the most powerful number, yet, it is the most rational, sane, and cool-headed number there is.
Can you guess what it is?
$$0$$
Multiplication by Zero
When multiplied, any real number $a$ is devoured by $0.$ $$ a\cdot 0=0\cdot a=0. $$
Example $$ 0\cdot \mbox{597,220,000,000,000,000,000,000}=0 $$ $0$ times the mass of earth in kilograms is $0.$
Zero Divided by a Number
Zero when divided by real number $a$ (except $0!$) is $0.$ $$ 0\div a=0\cdot \frac{1}{a}=0. $$
Example $$ 0\div\mbox{597,220,000,000,000,000,000,000}=\frac{0}{\mbox{597,220,000,000,000,000,000,000}}=0 $$ $0$ divided by the mass of earth in kilograms is $0.$
Division by Zero
What happens when we do this: $$ 15\div 0? $$ Let's ask a more straightforward question first...
Example
What happens when we do this: $$ 15\div 3? $$ No problem! $15\div 3$ asks the question, "how many groups of $3$ can we make from $15?$"
$15\div 3=5$ since we can make $5$ groups of $3$ from $15.$
Is it true yet?
Is it true yet?
Division by Zero
Returning to $$ 15\div 0 $$ Can we add $0$ to itself enough times to make $15?$
Is there a number $n$ that will make the statement below true? $$ 15=\underbrace{0+0+0+\cdots 0}_{ n\mbox{ of groups of } 0} $$ ever be true?

Conclusion?
Division by $0$ is undefined.
(...to the tune of "Over the River and Through the Woods")
(...to the tune of "Over the River and Through the Woods")
Division by Zero is Undefined
For any number $a$ (including $0!$), the quantity $$ a\div 0=\frac{a}{0} $$ is undefined.
Is there a meaningful interpretation of division by zero?

Teleportation!
Let's give a context to the expression $15\div 3.$
If we travel a distance of $15$ feet in $3$ seconds, the interpretation of the statement our rate of travel is $$ \displaystyle 15\div 3=\frac{15\mbox{ feet}}{3 \mbox{ second}}=5 \mbox{ feet/second} $$
Let's now consider the meaning of $15\div 0.$
This statement can be interpreted as having travelled $15$ feet in $0$ seconds.
If we travel $15$ feet in $0$ seconds, what is our rate of travel?
To get from point A to point B in $0$ seconds (instantaneously!) means we've teleported.
(...and divided by zero.)
(...and divided by zero.)
Public Service Announcement
Although zero may be the good-natured and sublimely content ruler of the universe, do not mess with zero.


Examples!
$-8\cdot 0$
$\displaystyle \frac{0}{-2}$
$\displaystyle \frac{-32}{0}$
$\displaystyle \frac{0}{n+5}$
$\displaystyle \frac{10-3p}{0}$
Solutions!
$-8\cdot 0=0$
$\displaystyle \frac{0}{-2}=0$
$\displaystyle \frac{-32}{0}$ is undefined (teleportation!)
$\displaystyle \frac{0}{n+5}=0$
$\displaystyle \frac{10-3p}{0}$ is undefined (teleportation!)
More Examples!
$-84n + (-73n) + 84n$
$\displaystyle \frac{7}{15}\cdot \frac{8}{23}\cdot \frac{15}{7}$
$\displaystyle \frac{3}{4}\cdot\frac{4}{3}(6x+12)$
More Solutions!
$ \begin{array}{lll} \displaystyle -84n + (-73n) + 84n&= \displaystyle -73n+(-84n) + 84n&\mbox{commutative property of addition}\\ &= \displaystyle -73n+0& \mbox{additive inverse property}\\ &= \displaystyle -73n& \mbox{additive identity property}\\ \end{array} $
$ \begin{array}{lll} \displaystyle \frac{7}{15}\cdot \frac{8}{23}\cdot \frac{15}{7}&= \displaystyle \frac{8}{23}\cdot \frac{7}{15}\cdot \frac{15}{7}&\mbox{commutative property of multiplication}\\ &= \displaystyle \displaystyle \frac{8}{23}\cdot 1& \mbox{multiplicative inverse property}\\ &= \displaystyle \displaystyle \frac{8}{23}& \mbox{multiplicative identity property}\\ \end{array} $
$ \begin{array}{lll} \displaystyle \frac{3}{4}\cdot\frac{4}{3}(6x+12)&= 1\cdot (6x+12)\displaystyle &\mbox{multiplicative inverse property}\\ &= \displaystyle 6x+12 &\mbox{multiplicative identity property}\\ \end{array} $
The Distributive Property
For any real numbers $a,$ $b,$ and $c,$ the following is always a true statement. $$ a(b+c)=ab+ac $$ "A product of a sum is the sum of the products."
Example $$2\cdot (3+4)=2\cdot 7=14$$ and $$2 \cdot 3+2 \cdot 4=6+8=14$$ Thus, $$ 2\cdot (3+4)=2 \cdot 3+2 \cdot 4 $$ "The double of the sum $3$ and $4$ is the sum of the doubles of $3$ and $4.$"
Other Forms of the Distributive Property
For any real numbers $a,$ $b,$ and $c,$ the following are always a true statements. $$ (b+c)a=ba+ca $$ $$ a(b-c)=ab-ac $$ $$ (b-c)a=ba-ca $$
Examples: Using the Distributive Property
$\displaystyle 3(x+4)$
$\displaystyle 8\left(\frac{3}{8}x+\frac{1}{4}\right)$
$100(0.3+0.25q)$
$-2(4y+1)$
$-11(4-3q)$
Solutions: Using the Distributive Property
$ \begin{array}{lll} \displaystyle 3(x+4)&= \displaystyle 3\cdot x+3\cdot 4&\mbox{distributive property}\\ &= \displaystyle 3x+12&\mbox{}\\ \end{array} $
$ \begin{array}{lll} \displaystyle 8\left(\frac{3}{8}x+\frac{1}{4}\right)&= \displaystyle 8\cdot\frac{3}{8}x+\cdot\frac{1}{4} &\mbox{distributive property}\\ &= \displaystyle 3x+2&\mbox{}\\ \end{array} $
$ \begin{array}{lll} \displaystyle 100(0.3+0.25q)&= \displaystyle 100\cdot 0.3+\cdot 0.25q&\mbox{distributive property}\\ &= \displaystyle 30+25q&\mbox{}\\ \end{array} $
$ \begin{array}{lll} \displaystyle -2(4y+1)&= \displaystyle -2\cdot 4y+(-2)\cdot 1)&\mbox{distributive property}\\ &= \displaystyle-8y-2 &\mbox{}\\ \end{array} $
$ \begin{array}{lll} \displaystyle -11(4-3a)&= \displaystyle -11(4+(-3a))&\mbox{subraction is the addition of opposites}\\ &= \displaystyle -11\cdot 4+(-11)\cdot(-3a) &\mbox{distributive property}\\ &= \displaystyle -44+33a &\mbox{}\\ \end{array} $
More Examples: Using the Distributive Property
$\displaystyle -(y+5)$
$\displaystyle 8-2(x+3)$
$4(x - 8) - (x + 3)$
Solutions: Using the Distributive Property
$ \begin{array}{lll} \displaystyle -(y+5)&= \displaystyle (-1)(y+5)&\mbox{}\\ &= \displaystyle (-1)y+(-1)5&\mbox{distributive property}\\ &= \displaystyle -y+(-5)&\mbox{}\\ &= \displaystyle -y-5&\mbox{addition of opposites is subtraction}\\ \end{array} $
$ \begin{array}{lll} \displaystyle 8-2(x+3)&= \displaystyle 8+(-2)(x+3)&\mbox{subraction is the addition of opposites}\\ &= \displaystyle 8+(-2)x+(-2)\cdot 3&\mbox{distributive property}\\ &= \displaystyle 8+(-2)x+(-6)&\mbox{distributive property}\\ &= \displaystyle 8-2x-6&\mbox{addition of opposites is subtraction}\\ &= \displaystyle -2x+8-6&\mbox{addition is commutative}\\ &= \displaystyle -2x+2&\mbox{addition is commutative}\\ \end{array} $
$ \begin{array}{lll} \displaystyle 4(x - 8) - (x + 3)&= 4x - 32 - x - 3\displaystyle &\mbox{distributive property}\\ &= \displaystyle 4x - x - 32 - 3&\mbox{addition is commutative}\\ &= \displaystyle 3x - 35&\mbox{combine like terms}\\ \end{array} $
All Together Now!

