Today, for the purposes of this course, we complete our number vocabulary with the real numbers.
Real numbers are essentially all possible decimal numbers.
Integers
Recall that the integers are the collection of numbers $$ \ldots,-5,-4,-3,-2,-1,0,1,2,3,4,5,\ldots $$

In the context of the real numbers, we can think of the integers as signed numbers with all zeros to the right of the decimal point.
The Rational Numbers
The rational numbers are the collection of all possible fractions.

In the context of the real numbers, the rational numbers consist of all terminating decimals and non-terminating, repeating decimals. Some examples are $$ 0.35=\frac{35}{100}=\frac{7}{20}, -\frac{1}{3}=0.333333333....=0.\overline{3}, \frac{5}{24}=0.208333333...=0.208\overline{3},\\ 1089=\frac{1089}{1}=1089.000000...=1089.\overline{0} $$
Formal Definition
A rational number is a number of the form $\displaystyle \frac{p}{q},$ where $p$ and $q$ are integers and $q \neq 0.$
A rational number can be written as the ratio of two integers.
Examples
Write $-27$ as a ratio of two integers.
Write $7.31$ as a ratio of two integers.
Solutions
$\displaystyle -27=\frac{-27}{1}$
$ \begin{array}{ll} \displaystyle 7.31&=\displaystyle7+\frac{31}{100}&\\ &=\displaystyle\frac{700}{100}+\frac{31}{100}&\\ &=\displaystyle\frac{731}{100}&\\ \end{array} $
Fact
Every rational number can be written as a terminating decimal, or non-terminating but repeating decimal.
Perfect Squares
A number that can be written as a number times itself is called a perfect square.
Examples include
$
\begin{array}{l}
1=1^2\\
4=2^2\\
9=3^2\\
16=4^2\\
25=5^2\\
\end{array}
$


In general the number $m$ is called a perfect square if $m=n^2$ for some number $n.$
Pop Quiz
Suppose we're given a number, say $100,$ and we want to know if it's a perfect square.
Is there a number $n$ such that $100=n^2?$
Square Roots
Since $100=10^2,$ we write $\sqrt{100}=10.$
In general, the positive number $n$ which gives us $m$ back when we square it is called the square root of $m.$
We denote $n$ as $\sqrt{m}.$
Square Roots
For positive real numbers, the following two statements say the same thing. $$ m=n^2 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, n=\sqrt{m} $$
Example $$ 100=10^2 \,\,\,\,\,\,\,\,\,\,\,\,\,\, 10=\sqrt{100} $$
Examples
Fill in the table.

Question
What about $\sqrt{2}?$
Is there a real number $n$ such that $n^2=2?$
Ancient Approximations
The Babylonians used $$ 1+\frac{24}{60}+\frac{51}{60^2}+\frac{10}{60^3}=\frac{305470}{216000}=1.41421\overline{296} $$ as an approximation of $\sqrt{2}.$

Ancient Approximations
Ancient approximations from India give $$ \sqrt{2}\approx 1+\frac{1}{3}+\frac{1}{3\cdot 4}+\frac{10}{3 \cdot 4 \cdot 34}=\frac{577}{408}=1.41421\overline{56862745098039} $$
These ancient approximations were close, but they weren't exact.
Burning Question
Can the exact value of $\sqrt{2}=1.41421356...$ be written as a fraction?
The Quick Answer

The Fun Answer
Ever hear of the Pythagoreans?
They were a cult of followers of Pythagoras (of Pythagorean Theorem fame).

After the death of Pythagoras, some Pythagorean circles became a full-on religion.
The Fun Answer
The Pythagoreans believed in a harmonious order of the universe.
Such harmonies are embodied in the ratios of numbers.
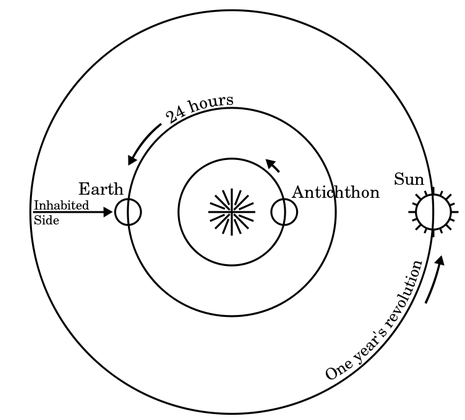
The Pythagoreans believed the celestial bodies orbited the "a central fire" at distances described by ratios.
Musical harmonies (intervals) are described by ratios of frequencies.
The notion of justice was rooted in the idea that "proportion ensured that each part receives what it is due."
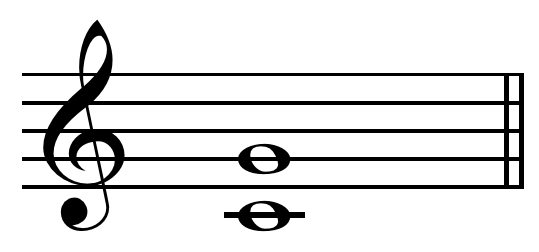

In Music
The Pythagoreans successfully described literal musical harmonies (intervals) as frequency ratios.
For example, the perfect fifth is has a frequency ratio of $3:2.$

To identical tones played at the same time (unison) is the ratio $1:1.$
The major third, another common frequency ratio in western music, is $3^4:2^6,$ or $81:64.$
The Harmony of the Spheres
This is all to say that the Pythagoreans believed that all numbers could be expressed as ratios of integer quantities.
The belief that all numbers were rational was a sacred underpinning of of their beliefs of the cosmic order.

The Harmony of the Spheres
So, the idea that there were numbers which could not be expressed as ratios of integers was a threat to the Pythagorean world view.
In other words, the Pythagoreans hated the idea that a number couldn't be rational.
Along Comes Hippasus
Hippasus is credited with discovering irrational numbers by proving that $\sqrt{2}=1.41421356...$ cannot be expressed as the ratio of two integers.

How do you think his Pythagorean sisters and brothers rewarded him for uncovering this inconvenient truth?
Big Fact
Some real numbers cannot be written as fractions.
Since any terminating or non-terminating but repeating decimal can be written as a fraction, we conclude that...
Irrational numbers are the non-terminating and non-repeating decimal numbers.
Irrational Numbers
$\sqrt{2}$ is the first irrational number known to humans. (With deadly consequences.)
Other famous irrational numbers include... $$ \begin{array}{lll} \pi &=3.14159... & \mbox{ pi, the ratio of any circle's circumference to its diameter}\\ \varphi &=\displaystyle \frac{1+\sqrt{5}}{2}=1.618033988749... & \mbox{the Golden Ratio}\\ e &=2.71828182845... & \mbox{Euler's Number}\\ \end{array} $$
The Real Numbers
The real numbers are the collection of the rational and irrational numbers.

Astonishing Fact
There are vastly more irrational numbers than rational numbers.

Identifying Numbers
Which of the following numbers $0.583,$ $0.47,$ $3.605551275...$ are
ⓐ rational numbers?
ⓑ irrational numbers?
Solution

Another Fact
Numbers of the form $\sqrt{m}$ are either irrational or integers.
$\sqrt{m}$ is an integer precisely when $m$ is a perfect square.
$\sqrt{m}$ is irrational precisely when $m$ is a not perfect square.
Examples
Identify the following numbers as rational or irrational:
ⓐ $\sqrt{49}$
ⓑ $\sqrt{50}$
Solutions
ⓐ $\sqrt{49}=7,$ so it's rational.
ⓑ Since $7\lt \sqrt{50} \lt 8,$ $50$ is not a perfect square, so it is an irrational decimal number.
Another Fun Question
What is $\sqrt{-25}?$
Another Fun Answer
$\sqrt{-25}$ is a number $n$ such that $n^2=-25.$
There is no real number which does this.
There is a richer system of numbers called the complex numbers where this is possible, but.....
...we won't cover them in this class.

Examples
For each number given, identify whether it is a real number or not a real number:
ⓐ $\sqrt{-169}$
ⓑ $- \sqrt{64}.$
Solutions
ⓐ $\sqrt{-169}$ is not a real number since no real number $n$ satisfies $n^2=-169$
ⓑ $- \sqrt{64}=-8.$ This number can be read as the opposite of $\sqrt{64}.$
Examples
Classify the following numbers as whole numbers, integers, rational numbers, irrational numbers, and real numbers by circling all that apply.
| $\displaystyle -7$ | whole | integer | rational | irrational | real |
| $\displaystyle \frac{14}{5}$ | whole | integer | rational | irrational | real |
| $\displaystyle 8$ | whole | integer | rational | irrational | real |
| $\displaystyle \sqrt{5}$ | whole | integer | rational | irrational | real |
| $\displaystyle 5.9$ | whole | integer | rational | irrational | real |
| $\displaystyle -\sqrt{64}$ | whole | integer | rational | irrational | real |
Solutions

Fact
Just like whole numbers and integers, every rational number has a home on the number line.
For example, let's consider the following numbers $$ \frac{1}{5},\,\,\,-\frac{4}{5},\,\,\,3,\,\,\,\frac{7}{4},\,\,\,-\frac{9}{2},\,\,\,-5,\,\,\,\frac{8}{3} $$ and their place on the number line.

The number line imposes a natural order on its residents.
The further to the right a number is, the larger it is.

So, $$ -5 \lt -\frac{9}{2} \lt - \frac{4}{5} \lt \frac{1}{5} \lt \frac{4}{5} \lt \frac{7}{4} \lt \frac{8}{3}\lt 3 $$ We may also write $$ 3 \gt \frac{8}{3} \gt \frac{7}{4} \gt \frac{4}{5} \gt \frac{1}{5} \gt -\frac{4}{5} \gt -\frac{9}{2} \gt -5 $$
Example
Order each of the following pairs of numbers, using $\lt$ or $\gt.$
$\displaystyle \frac{7}{3} \underline{\hspace{2cm}} \frac{6}{5}$
$\displaystyle -\frac{5}{2} \underline{\hspace{2cm}} -3$
$\displaystyle \frac{3}{4} \underline{\hspace{2cm}} \frac{6}{5}$
$\displaystyle -\frac{5}{2} \underline{\hspace{2cm}} -\frac{1}{4}$
Plot each pair on the number line.

Example
Order each of the following pairs of numbers, using $\lt$ or $\gt.$
$\displaystyle \frac{7}{3} \gt \frac{6}{5}$
$\displaystyle -\frac{5}{2} \gt -3$
$\displaystyle \frac{3}{4} \lt \frac{6}{5}$
$\displaystyle -\frac{5}{2} \lt -\frac{1}{4}$
Plot each pair on the number line.

Fact
Just like whole numbers and integers, and rational numbers, every decimal number (real number!) has a home on the number line.
Examples
Locate $-0.74$ on the number line.

Locate $0.04$ and $0.4$ on the number line. Decide which is larger.

Solutions
Locate $-0.74$ on the number line.

Locate $0.04$ and $0.4$ on the number line. Decide which is larger.

From the number line we see that $0.04 \lt 0.4.$
We can also see this by writing $\displaystyle 0.04=\frac{4}{100}$ and $\displaystyle 0.4=\frac{4}{10}=\frac{40}{100}.$
Forty one hundredths is greater than four one hundredths.
Examples
Order $0.64$ _____ $0.6$ using $\lt$ or $\gt$
Order $0.83$ _____ $0.803$ using $\lt$ or $\gt$
Order $-0.1$ _____ $-0.8$ using $\lt$ or $\gt$
If necessary, use a number line to locate and compare the numbers.

Solutions
$\displaystyle 0.64=\frac{64}{100} \gt \frac{60}{100} = 0.6$
$\displaystyle 0.83=\frac{83}{100}=\frac{830}{1000} \gt \frac{803}{1000}=0.803$
$\displaystyle -0.1 \gt -0.8$
