We continue with operations on fractions.
Of course, we've saved the best for last. ;)
By the end of today, we'll be able to do some honest-to-goodness applications!
Adding and Subtracting with Like Denominators
With like denominators, adding and subtracting is relatively easy-breezy. $$ \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c} $$ and $$ \frac{a}{c}-\frac{b}{c}=\frac{a-b}{c} $$
Examples $$ \frac{4}{7}+\frac{1}{7}=\frac{4+1}{7}=\frac{5}{7} $$ $$ \frac{4}{7}-\frac{1}{7}=\frac{4-1}{7}=\frac{3}{7} $$
Examples
$ \displaystyle \frac{x}{3}+\frac{2}{3} $
$ \displaystyle -\frac{23}{24}-\frac{13}{24} $
$ \displaystyle -\frac{10}{x}-\frac{4}{x} $
$ \displaystyle \frac{3}{8}+\left(-\frac{5}{8}\right)-\frac{1}{8} $
Solutions
$$ \frac{x}{3}+\frac{2}{3}=\frac{x+2}{3} $$
$$ \begin{array}{lll} \displaystyle -\frac{23}{24}-\frac{13}{24}&=\displaystyle \frac{-23}{24}-\frac{13}{24}&\mbox{put minus upstairs}\\ &=\displaystyle \frac{-23-13}{24}&\mbox{}\\ &=\displaystyle \frac{-36}{24}&\\ &=\displaystyle -\frac{36}{24}&\\ &=\displaystyle -\frac{3}{2}&\mbox{simplify}\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle -\frac{10}{x}-\frac{4}{x}&=\displaystyle \frac{-10}{x}-\frac{4}{x}&\mbox{put minus upstairs}\\ &=\displaystyle \frac{-10-4}{x}&\\ &=\displaystyle \frac{-14}{x}&\\ &=\displaystyle -\frac{14}{x}&\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle \frac{3}{8}+\left(-\frac{5}{8}\right)-\frac{1}{8}&=\displaystyle \frac{3}{8}+\frac{-5}{8}-\frac{1}{8}&\mbox{put minus upstairs}\\ &=\displaystyle \frac{3+(-5)-1}{8}&\\ &=\displaystyle \frac{-3}{8}&\\ &=\displaystyle -\frac{3}{8}&\\ \end{array} $$
Question
What happens if we don't have the same denominator?

Answer
We get greedy!


Examples
$ \displaystyle \frac{7}{12}+\frac{5}{18} $
$ \displaystyle \frac{7}{15}-\frac{19}{24} $
Solutions
$$ \begin{array}{lll} \displaystyle \frac{7}{12}+\frac{5}{18}&=\displaystyle \frac{7}{2 \cdot 2 \cdot 3}+\frac{5}{2 \cdot 3 \cdot 3}&\mbox{factor denominators}\\ &=\displaystyle \frac{7\cdot \color{magenta}{3}}{2 \cdot 2 \cdot 3\cdot \color{magenta}{3}}+\frac{5\cdot \color{magenta}{2}}{2 \cdot 3 \cdot 3\cdot \color{magenta}{2}}&\mbox{denominators get greedy!}\\ &=\displaystyle \frac{21}{36}+\frac{10}{36}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{31}{36}&\mbox{combine over common denominator}\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle \frac{7}{15}-\frac{19}{24}&=\displaystyle \frac{7}{3 \cdot 5}-\frac{19}{2 \cdot 2 \cdot 2 \cdot 3}&\mbox{factor denominators}\\ &=\displaystyle \frac{7 \cdot \color{magenta}{2} \cdot \color{magenta}{2} \cdot \color{magenta}{2}}{3 \cdot 5 \cdot \color{magenta}{2} \cdot \color{magenta}{2} \cdot \color{magenta}{2}}-\frac{19\cdot \color{magenta}{5}}{2 \cdot 2 \cdot 2 \cdot 3 \cdot \color{magenta}{5}}&\mbox{denominators get greedy!}\\ &=\displaystyle \frac{56}{120}-\frac{95}{120}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{56-95}{120}&\mbox{}\\ &=\displaystyle \frac{-39}{120}&\mbox{combine over common denominator}\\ &=\displaystyle \frac{-13 \div 3}{120\div 3}&\mbox{divide out common factors}\\ &=\displaystyle \frac{-13}{40}&\mbox{}\\ \end{array} $$
The Greedy-Little-Piggy Method
Step 1: Factor all denominators.
Step 2: Build up denominators making sure each greedy denominator has what every other greedy denominator has.
Step 3: Multiply out numerators and denominators. This step should result in a common denominator.
Step 4: Combine over a common denominator.
Step 5: In necessary, simply the result, i.e., divide out common factors.
Examples
$ \displaystyle \frac{3}{5}+\frac{x}{8} $
$ \displaystyle \frac{5x}{6}-\frac{3}{10} $
Solutions
$$ \begin{array}{lll} \displaystyle \frac{3}{5}+\frac{x}{8}&=\displaystyle \frac{3}{5}+\frac{x}{2\cdot 2 \cdot 2}&\mbox{factor denominators}\\ &=\displaystyle \frac{3\cdot \color{magenta}{2}\cdot \color{magenta}{2}\cdot \color{magenta}{2}}{5 \cdot \color{magenta}{2}\cdot \color{magenta}{2}\cdot \color{magenta}{2}}+\frac{x\cdot \color{magenta}{5}}{2\cdot 2 \cdot 2\cdot \color{magenta}{5}}&\mbox{denominators get greedy!}\\ &=\displaystyle \frac{24}{40}+\frac{5x}{40}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{24+5x}{40}&\mbox{combine over common denominator}\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle \frac{5x}{6}-\frac{3}{10}&=\displaystyle \frac{5x}{2 \cdot 3}-\frac{3}{2\cdot 5}&\mbox{factor denominators}\\ &=\displaystyle \frac{5x \cdot \color{magenta}{5} }{2 \cdot 3 \cdot \color{magenta}{5}}-\frac{3 \cdot \color{magenta}{3}}{2\cdot 5 \cdot \color{magenta}{3}}&\mbox{denominators get greedy!}\\ &=\displaystyle \frac{25x}{30}-\frac{9}{30}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{25x-9}{30}&\mbox{combine over common denominator}\\ \end{array} $$
Whadda you say we lighten things up and talk about complex fractions?


Examples
$ \displaystyle \frac{\displaystyle \left(\frac{1}{2}\right)^2}{4+3^2} $
$ \displaystyle \frac{\displaystyle \frac{1}{2}+\frac{2}{3}}{\displaystyle \frac{3}{4}-\frac{1}{6}} $
Solutions
$$ \begin{array}{lll} \displaystyle \frac{\displaystyle \left(\frac{1}{2}\right)^2}{4+3^2}&=\displaystyle \frac{\displaystyle \frac{1}{4}}{4+9}&\mbox{follow order of ops}\\ &=\displaystyle \frac{\displaystyle \frac{1}{4}}{13}&\mbox{simplify}\\ &=\displaystyle \frac{1}{4}\div 13&\mbox{express as division}\\ &=\displaystyle \frac{1}{4}\cdot \frac{1}{13}&\mbox{invert and multiply}\\ &=\displaystyle \frac{1}{52}&\mbox{}\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle \frac{\displaystyle \frac{1}{2}+\frac{2}{3}}{\displaystyle \frac{3}{4}-\frac{1}{6}}&=\displaystyle \frac{\displaystyle \frac{1}{2}+\frac{2}{3}}{\displaystyle \frac{3}{2\cdot 2}-\frac{1}{2\cdot 3}}&\mbox{factor denominators}\\ &=\displaystyle \frac{\displaystyle \frac{1\cdot \color{magenta}{3}}{2\cdot \color{magenta}{3}}+\frac{2\cdot \color{magenta}{2}}{3\cdot \color{magenta}{2}}}{\displaystyle \frac{3 \cdot \color{magenta}{3}}{2\cdot 2 \cdot \color{magenta}{3}}-\frac{1\cdot \color{magenta}{2}}{2\cdot 3\cdot \color{magenta}{2}}}&\mbox{denominators get greedy!}\\ &=\displaystyle \frac{\displaystyle \frac{3}{6}+\frac{4}{6}}{\displaystyle \frac{9}{12}-\frac{2}{12}}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{\displaystyle \frac{7}{6}}{\displaystyle \frac{7}{12}}&\mbox{combine over common denominators}\\ &=\displaystyle \displaystyle \frac{7}{6}\div \frac{7}{12}&\mbox{express as division}\\ &=\displaystyle \displaystyle \frac{7}{6}\cdot \frac{12}{7}&\mbox{invert and multiply}\\ &=\displaystyle \displaystyle \frac{7 \cdot 12}{6 \cdot 7}&\mbox{}\\ &=\displaystyle \displaystyle \frac{12}{6}&\mbox{cancel out $7$s}\\ &=\displaystyle \displaystyle \frac{2}{1}&\mbox{reduce}\\ &=\displaystyle 2&\mbox{simplify}\\ \end{array} $$
And what's our reward for going to all this trouble to learn fraction arithmetic?


Evaluating Expressions with Fractional Values
We may now evaluate expressions with values which are fractions!

Example
Evaluate the expression $\displaystyle x+\frac{1}{3}$ with the values $\displaystyle x=-\frac{1}{3}$ and $\displaystyle x=-\frac{3}{4}.$
Solution
For $\displaystyle x=-\frac{1}{3}$ $$ \begin{array}{lll} \displaystyle x+\frac{1}{3} &=\displaystyle -\frac{1}{3}+\frac{1}{3}&\mbox{since $x=-\frac{1}{3}$}\\ &=\displaystyle \frac{-1}{3}+\frac{1}{3}&\mbox{put negative upstairs}\\ &=\displaystyle \frac{-1+1}{3}&\mbox{combine over common denominator}\\ &=\displaystyle \frac{0}{3}&\mbox{simplfy}\\ &=\displaystyle 0&\mbox{since $0$ over (almost!) anything is $0$}\\ \end{array} $$
For $\displaystyle x=-\frac{3}{4}$ $$ \begin{array}{lll} \displaystyle x+\frac{1}{3} &=\displaystyle -\frac{3}{4}+\frac{1}{3}&\mbox{since $x=-\frac{3}{4}$}\\ &=\displaystyle \frac{-3}{4}+\frac{1}{3}&\mbox{put negative upstairs}\\ &=\displaystyle \frac{-3}{2 \cdot 2}+\frac{1}{3}&\mbox{factor denominators}\\ &=\displaystyle \frac{-3\cdot \color{magenta}{3}}{2 \cdot 2 \cdot \color{magenta}{3}}+\frac{1\cdot \color{magenta}{2}\cdot \color{magenta}{2}}{3\cdot \color{magenta}{2}\cdot \color{magenta}{2}}&\mbox{Denominators are greedy little piggies!}\\ &=\displaystyle \frac{-9}{12}+\frac{4}{12}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{-9+4}{12}&\mbox{combine over common denominator}\\ &=\displaystyle \frac{-5}{12}&\mbox{simplify}\\ &=\displaystyle -\frac{5}{12}&\mbox{put negative out front}\\ \end{array} $$
Examples
Evaluate the expression $\displaystyle -\frac{5}{6}-y$ when $\displaystyle y=-\frac{2}{3}.$
Evaluate the expression $\displaystyle 2 x^2 y$ when $\displaystyle x=\frac{1}{4}$ and $\displaystyle y=-\frac{2}{3}.$
Evaluate the expression $\displaystyle \frac{p+q}{r}$ when $\displaystyle p=-4,$ $\displaystyle q=-2,$ and $\displaystyle r=8.$
Solutions
$$ \begin{array}{lll} \displaystyle -\frac{5}{6}-y&=\displaystyle -\frac{5}{6}-\left(-\frac{2}{3}\right) &\mbox{ since $\displaystyle y=-\frac{2}{3}.$}\\ &=\displaystyle -\frac{5}{6}+\frac{2}{3}&\mbox{subtraction is the addition of opposites!}\\ &=\displaystyle -\frac{5}{2 \cdot 3}+\frac{2}{3}&\mbox{factor denominators}\\ &=\displaystyle -\frac{5}{2 \cdot 3}+\frac{2\cdot\color{magenta}{2}}{3\cdot\color{magenta}{2}}&\mbox{We all know what denominators are!}\\ &=\displaystyle -\frac{5}{6}+\frac{4}{6}&\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{-5}{6}+\frac{4}{6}&\mbox{negative goes upstairs}\\ &=\displaystyle \frac{-5+4}{6}&\mbox{combine over common denominator}\\ &=\displaystyle \frac{-1}{6}&\mbox{simplify}\\ &=\displaystyle -\frac{1}{6}&\mbox{simplify}\\ \end{array} $$
$$ \begin{array}{lll} \displaystyle 2 x^2 y&=\displaystyle 2 \left(\frac{1}{4}\right)^2 \left(-\frac{2}{3}\right) &\mbox{since $\displaystyle x=\frac{1}{4}$ and $\displaystyle y=-\frac{2}{3}.$}\\ &=\displaystyle 2 \cdot \frac{1}{16}\cdot \left(-\frac{2}{3}\right) &\mbox{}\\ &=\displaystyle -\frac{2}{1} \cdot \frac{1}{16} \cdot \frac{2}{3} &\mbox{result will be negative}\\ &=\displaystyle -\frac{2\cdot 1 \cdot 2}{1\cdot 16\cdot 3} &\mbox{multiply numerators and denominators}\\ &=\displaystyle -\frac{2\cdot 1 \cdot 2}{1\cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 3} &\mbox{factor}\\ &=\displaystyle -\frac{1}{1\cdot 2 \cdot 2 \cdot 3} &\mbox{cancel two $2$s}\\ &=\displaystyle -\frac{1}{12} &\mbox{simplify}\\ \end{array} $$ Note: When multiplying, there is no need to find common denominators.
$$ \begin{array}{lll} \displaystyle \frac{p+q}{r}&=\displaystyle \frac{-4+(-2)}{8}&\mbox{since $\displaystyle p=-4,$ $\displaystyle q=-2,$ and $\displaystyle r=8.$}\\ &=\displaystyle \frac{-6}{8} &\mbox{follow order of ops}\\ &=\displaystyle \frac{-6\div 2}{8\div 2} &\mbox{divide out a $2$ (cancel common factor of $2$)}\\ &=\displaystyle \frac{-3}{4} &\mbox{}\\ &=\displaystyle -\frac{3}{4} &\mbox{finshing touch: put minus out front}\\ \end{array} $$
Application of Complex Fractions
Electrical Resistance: The total resistance $R$ in a parallel circuit with two individual resistors $r_1$ and $r_2$ can be calculated by using the formula $$R=\frac{1}{\displaystyle \frac{1}{r_1}+\frac{1}{r_2}}.$$
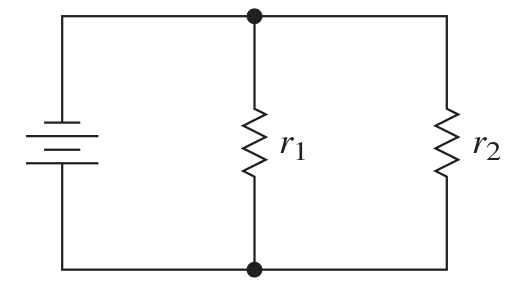
Solution
When $r_1=18$ ohms and $r_2=8$ ohms,
$$ \begin{array}{lll} \displaystyle R&=\displaystyle \frac{1}{\displaystyle \frac{1}{r_1}+\frac{1}{r_2}} &\mbox{}\\ &=\displaystyle \frac{1}{\displaystyle \frac{1}{18}+\frac{1}{8}} &\mbox{since $r_1=18$ ohms and $r_2=8$ ohms}\\ &=\displaystyle \frac{1}{\displaystyle \frac{1}{3\cdot 3 \cdot 2}+\frac{1}{2\cdot 2\cdot 2}} &\mbox{factor denominators}\\ &=\displaystyle \frac{1}{\displaystyle \frac{1\cdot \color{magenta}{2}\cdot \color{magenta}{2}}{3\cdot 3 \cdot 2 \cdot \color{magenta}{2}\cdot \color{magenta}{2}}+\frac{1 \cdot \color{magenta}{3}\cdot \color{magenta}{3}}{2\cdot 2\cdot 2 \cdot \color{magenta}{3}\cdot \color{magenta}{3}}} &\mbox{Greedy Little Piggies!}\\ &=\displaystyle \frac{1}{\displaystyle \frac{4}{72}+\frac{9}{72}} &\mbox{multiply out numerators and denominators}\\ &=\displaystyle \frac{1}{\displaystyle \frac{4+9}{72}} &\mbox{combine over common denominator}\\ &=\displaystyle \frac{1}{\displaystyle \frac{13}{72}} &\mbox{simplify}\\ &=\displaystyle 1\div \frac{13}{72} &\mbox{express as division problem}\\ &=\displaystyle 1\cdot \frac{72}{13} &\mbox{invert and multiply}\\ &=\displaystyle \frac{72}{13} &\mbox{simplify}\\ \end{array} $$ The total resistance in the circuit is $\displaystyle R = \frac{72}{13}$ohms, or $\displaystyle 5\frac{7}{13}$ ohms.
As a decimal, $R \approx 5.54$ ohms