Whole numbers and integers are awesome... right?
But to do more awesome things, we need to expand our number vocab.

Fractions: The Big Idea
Take a whole of something, and slice it up into parts all of an equal size.
Example
Take a pie, cut it up into $3$ equally sized pieces. Each piece is one third, or $\displaystyle \frac{1}{3}$ of the whole.
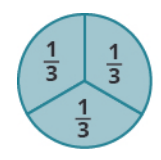
Example
Two of the three slices represents two thirds, or $\displaystyle \frac{2}{3},$ of the pie.
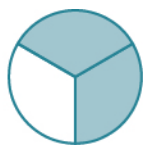
Definition
A fraction is a number that represents parts of a whole.
If the whole has been divided into $b$ equal pieces, and there are $a$ of these pieces, we represent this quantity as $$\displaystyle \frac{a}{b}$$ The number $b$ is called the denominator, and the number $a$ is called the numerator.
Property of One
Suppose a pie is cut up into $6$ equally-sized pieces.
If all $6$ of these pieces are present, how much of a pie do we have?
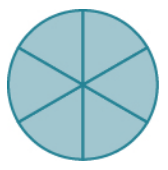
Property of One
Six out of six pieces is one whole, or $1.$ This is represented as $$ \frac{6}{6}=1. $$

This is the idea behind the following property of one.
Property of One
Suppose a whole is cut into $b$ equally sized pieces.
Then $b$ of these pieces gives us a whole. That is, $$ \frac{b}{b}=1. $$
Equivalent Fractions
Different representations of a fraction can still be the same quantity.
For example, suppose we cut up a one pizza into halves and the other pizza into eighths.
The amount of pizza on the left is represented as $\displaystyle \frac{1}{2},$ and the amount of pizza on the right is represented as $\displaystyle \frac{4}{8}.$ However, it is plainly visible that both quantities are the same.
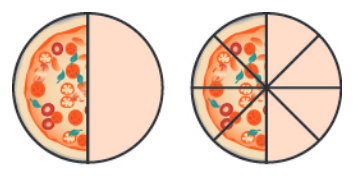 $$\displaystyle \frac{1}{2}=\frac{4}{8}$$
$$\displaystyle \frac{1}{2}=\frac{4}{8}$$
Equivalent Fractions
Two fractions with different representations but have the same value are called equivalent fractions.
Example: $\displaystyle \frac{1}{2}=\frac{4}{8}$
Equivalent Fractions
If we were to cut each half of the pizza into $4$ pieces, it would give us pizza cut into $8$ pieces.

This idea is expressed as $\displaystyle \frac{1}{2}=\frac{1\cdot 4}{2\cdot 4}=\frac{4}{8}.$
Equivalent Fractions Property
For any numbers $a,$ $b,$ and $c,$ it is true that $$ \frac{a}{b}=\frac{a\cdot c}{b\cdot c} $$
Example
$$ \frac{1}{2}=\frac{1\cdot 2}{2\cdot 2}=\frac{1\cdot 3}{2\cdot 3}=\frac{1\cdot 4}{2\cdot 4}=\frac{1\cdot 5}{2\cdot 5}=\frac{1\cdot 6}{2\cdot 6}=\cdots $$ or $$ \frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\frac{4}{8}=\frac{5}{10}=\frac{6}{12}=\cdots $$
Example
Name some equivalent fractions for $\displaystyle \frac{2}{5}.$
Simplifying Fractions
The equivalent fractions property is a gift from the universe.
We can use it to make a fraction with a denominator that we need. For example, if we needed to express $\displaystyle \frac{2}{5}$ with a denominator of $15,$ we could do it.
On the other hand, what is the universe hands us the fraction $\displaystyle \frac{6}{15}?$ How could we get back to $\displaystyle \frac{2}{5}?$
The answer...
Simplifying Fractions
Use the equivalent fractions property in reverse! $$ \frac{6}{15}=\frac{2\cdot 3}{5\cdot 3}=\frac{2}{5} $$

In other words, we can "cancel" common factors in the numerator and denominator.
Example
Simplify $\displaystyle \frac{32}{56}$ by expressing it in lowest terms.
Solution
$$ \begin{array}{lll} \displaystyle \frac{32}{56}&=\displaystyle \frac{4\cdot 8}{7\cdot 8}&\mbox{$8$ is a common factor in the numerator and denominator}\\ &=\displaystyle \frac{4}{7}&\mbox{cancel common factor}\\ \end{array} $$
A Method for Simplifying Fractions
Step 1: Factor the numerator and denominator into prime factors.
Step 2: Cancel common factors.
Step 3: If necessary, multiply leftover factors.
Example: Simplify $\displaystyle \frac{32}{56}.$
Example
Simplify $\displaystyle -\frac{210}{385}.$
Solution
$$ \begin{array}{lll} \displaystyle -\frac{210}{385}&=\displaystyle -\frac{2 \cdot 3 \cdot 5 \cdot 7}{5 \cdot 7\cdot 11}&\mbox{factor numerator and denominator into prime factors}\\ &=\displaystyle -\frac{2\cdot 3}{11}&\mbox{cancel common factors}\\ &=\displaystyle -\frac{6}{11}&\mbox{multiply leftover factors}\\ \end{array} $$
Example
Simplify $\displaystyle \frac{5x}{5y}.$
Solution
$$ \begin{array}{lll} \displaystyle \frac{5x}{5y}&=\displaystyle \frac{5 \cdot x}{5 \cdot y}&\mbox{factor numerator and denominator}\\ &=\displaystyle \frac{x}{y}&\mbox{cancel common factors}\\ \end{array} $$
Multiplying Fractions
Question: What is $\displaystyle \frac{1}{2}$ of $\displaystyle \frac{3}{4}?$
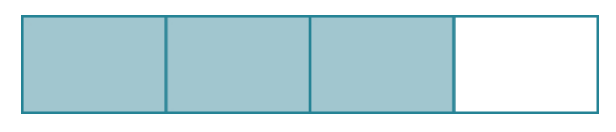
Multiplying Fractions
What is $\displaystyle \frac{1}{2}$ of $\displaystyle \frac{3}{4}?$

Any takers?
Multiplying Fractions
$$\displaystyle \frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$$

Multiplying Fractions
In general, $$ \frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d} $$
Example
Multiply $\displaystyle -\frac{11}{12}\cdot\frac{5}{7}$
Solution
$$ \begin{array}{lll} \displaystyle -\frac{11}{12}\cdot\frac{5}{7}&=\displaystyle -\frac{55}{84}&\mbox{multply numerators and denominators} \end{array} $$
Example
Multiply $\displaystyle -\frac{12}{5}(-20x)$
Solution
$$ \begin{array}{lll} \displaystyle -\frac{12}{5}(-20x)&=\displaystyle -\frac{12}{5}\left(\frac{-20x}{1}\right)&\mbox{express $20x$ as a fractions}\\ &=\displaystyle \frac{12\cdot 20 x}{5 \cdot 1}&\mbox{multiply numerators and denominators}\\ &=\displaystyle \frac{2\cdot 2 \cdot 3 \cdot 2 \cdot 2 \cdot 5 \cdot x}{5\cdot 1}&\mbox{factor numerators and denominators}\\ &=\displaystyle \frac{2\cdot 2 \cdot 3 \cdot 2 \cdot 2 \cdot x}{1}&\mbox{cancel common factors}\\ &=\displaystyle \frac{48 x}{1}&\mbox{multiply leftovers}\\ &=\displaystyle 48 x&\mbox{anything over 1 is itself}\\ \end{array} $$
Dividing Fractions
We'll get to the serious business of dividing fractions.
But first... questions!
Question #1: How many quarters fit into one half?
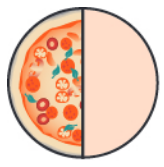
Question #2: How do we represent the above?
Dividing Fractions
We have demonstrated that $$ \frac{1}{2}\div \frac{1}{4}=2 $$ Is there a more efficient way than drawing pictures?
Dividing Fractions
$\displaystyle \frac{a}{b}\div$ $\displaystyle \frac{c}{d}$ $\displaystyle =\frac{a}{b} \cdot $ $\displaystyle \frac{d}{c}$
To divide a fraction $\displaystyle \frac{a}{b}$ by $\displaystyle \frac{c}{d},$ invert and multiply. That is, multiply $\displaystyle \frac{a}{b}$ by $\displaystyle \frac{d}{c}.$
Example
$\displaystyle \frac{1}{2}\div$ $\displaystyle \frac{1}{4}$ $\displaystyle =\frac{1}{2} \cdot $ $\displaystyle \frac{4}{1}$$=\displaystyle \frac{4}{2}=\frac{2}{1}=2$
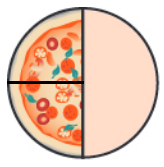
Two quarters fit into one half.
Vocab
The numbers
$\displaystyle \frac{c}{d}$ and $\displaystyle \frac{d}{c}$
are called reciprocals of another.
Question: What do we get when we multiply reciprocals?
Example
The numbers
$\displaystyle -\frac{10}{7}$ and $\displaystyle -\frac{-7}{10}$
are reciprocals. And $$ \left(-\frac{10}{7}\right)\left(-\frac{7}{10}\right)=\frac{10 \cdot 7}{7 \cdot 10}=1 $$
Multiplying Reciprocals
$$ \frac{a}{b}\cdot\frac{b}{a}=\frac{a\cdot b}{b \cdot a}=1 $$
Examples
Divide.
ⓐ $ \displaystyle -\frac{2}{3}\div\frac{n}{5} $
ⓑ $ \displaystyle -\frac{7}{8}\div\left(-\frac{14}{27}\right) $
Solutions
Divide.
ⓐ $ \displaystyle -\frac{2}{3}\div\frac{n}{5}=-\frac{2}{3}\cdot\frac{5}{n}=-\frac{10}{3n} $
ⓑ $ \displaystyle -\frac{7}{8}\div\left(-\frac{14}{27}\right)=\frac{7}{8}\cdot\frac{27}{14} =\frac{7\cdot 3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 2\cdot 7} =\frac{3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 2} =\frac{27}{16} $
Application
has $12$ cups of rose fertilizer.
The fertilizer box recommends $\displaystyle \frac{1}{4}$ cup for each rose bush.
How many rose bushes can be fertilized with the $12$ cups?
Wanna see something really scary?


Complex Fractions
A complex fraction is a fraction whose numerator and denominator are also fractions!
That is, they're expressions of the form $$ \frac{\displaystyle\frac{a}{b}}{\displaystyle\frac{c}{d}} $$ Pretty scary, huh?
Complex Fractions
Oh come on! It's not that scary!
Here's why... $$ \frac{\displaystyle\frac{a}{b}}{\displaystyle\frac{c}{d}}=\frac{a}{b}\div \frac{c}{d} $$
Examples
Simplify.
ⓐ $ \displaystyle\frac{\displaystyle\frac{3}{4}}{\displaystyle\frac{5}{8}} $
ⓑ $ \displaystyle\frac{\displaystyle\frac{x}{2}}{\displaystyle\frac{xy}{6}} $
Solutions
ⓐ $$ \begin{array}{lll} \displaystyle\frac{\displaystyle\frac{3}{4}}{\displaystyle\frac{5}{8}}&=\displaystyle \frac{3}{4}\div \frac{5}{8} &\mbox{express as division}\\ &=\displaystyle \frac{3}{4}\cdot \frac{8}{5} &\mbox{invert an multiply}\\ &=\displaystyle \frac{3\cdot 8}{4\cdot 5} &\mbox{perform multiplication}\\ &=\displaystyle \frac{3\cdot 2 \cdot 2 \cdot 2}{2\cdot 2\cdot 5} &\mbox{factor}\\ &=\displaystyle \frac{3\cdot 2 }{ 5} &\mbox{cancel}\\ &=\displaystyle \frac{6}{ 5} &\mbox{multiply leftovers}\\ \end{array} $$
ⓑ $$ \begin{array}{lll} \displaystyle\frac{\displaystyle\frac{x}{2}}{\displaystyle\frac{xy}{6}}&=\displaystyle \frac{x}{2}\div \frac{xy}{6}&\mbox{express as division}\\ &=\displaystyle \frac{x}{2}\cdot \frac{6}{xy}&\mbox{invert an multiply}\\ &=\displaystyle \frac{x\cdot 6}{2\cdot xy}&\mbox{perform multiplication}\\ &=\displaystyle \frac{x\cdot 2\cdot 3}{2\cdot x \cdot y}&\mbox{factor}\\ &=\displaystyle \frac{3}{y}&\mbox{cancel; Bob's your uncle!}\\ \end{array} $$
Simplifying Expressions with Fraction Bars
We've seen that $$ (\mbox{stuff on top})\div(\mbox{stuff on bottom})=\frac{\mbox{stuff on top}}{\mbox{stuff on bottom}} $$ The parentheses on the left tell us that fraction bars are a kind of grouping symbol.
Grouping Symbols Redux
We may now add a fifth kind grouping symbol to our list. Fraction bars!
Parentheses $(\, )$
Brackets $[ \, ]$
Braces $\{ \, \}$
Absolute Value $|\,|$
Fraction bars $\displaystyle \frac{\mbox{stuff on top}}{\mbox{stuff on bottom}}$
Examples
Simplify.
ⓐ $ \displaystyle \frac{4-2(3)}{2^2+2} $
ⓑ $ \displaystyle \frac{4(-3)+6(-2)}{-3(2)-2} $
Solutions
Divide.
ⓐ $$ \begin{array}{lll} \displaystyle \frac{4-2(3)}{2^2+2}&=\displaystyle \frac{4-6}{4+2}&\mbox{do order of ops in the top and bottom first}\\ &=\displaystyle \frac{-2}{6}&\mbox{}\\ &=\displaystyle -\frac{2\cdot 1}{2 \cdot 3}&\mbox{with experience, you're welcome to skip this step}\\ &=\displaystyle -\frac{1}{3}&\mbox{}\\ \end{array} $$
ⓑ $$ \begin{array}{lll} \displaystyle \frac{4(-3)+6(-2)}{-3(2)-2}&=\displaystyle \frac{-12+(-12)}{-6-2}&\mbox{do order of ops in the top and bottom first}\\ &=\displaystyle \frac{-24}{-8}&\mbox{}\\ &=\displaystyle 3&\mbox{}\\ \end{array} $$
Example
Translate the English phrase into an algebraic expression: the quotient of the difference of $m$ and $n,$ and $p.$
Hint: The word "quotient" synonymous with words "division" and fraction "fraction."
Solution
The difference of $m$ and $n$ is $m-n.$
So, the quotient of the difference of $m$ and $n,$ and $p$ is expressed as $$ \frac{m-n}{p} $$