Last time we recalled integer addition and subtraction.
Today, we recall integer multiplication and division.
The Idea of Integer Multiplication
Recall that multiplication is repeated addition. For example, $5\cdot 3$ means $3$ added to itself $5$ times, or $3+3+3+3+3,$ which is $15.$
This can be visualized in the following way.

The Idea of Integer Multiplication
With integer multiplication, the question arises about what to do with negative numbers.
For example, what does $5(-3)$ mean?
Using the above idea as a guide, $5(-3)$ simply means $-3$ added to itself $5$ times, or $-3+(-3)+(-3)+(-3)+(-3),$ which is _______.





The Idea of Integer Multiplication
We could then ask the question, what does $(-5)\cdot 3$ mean?
We can interpret $(-5)\cdot 3$ as $-5$ added to itself $3$ times, or $-5+(-5)+(-5),$ which is $-15$ as above.



Negative Times Negative
Of course, we've saved the best for last.
What does $(-5)(-3)$ mean?
Visualizing Negative Times Negative
Above, we saw that $(-5)\cdot 3$ to means "add $-5$ a total of $3$ times."
Thus, we interpret $(-5)\cdot (-3)$ to mean "subtract $-5$ a total of $3$" times."
We visualize $(-5)(-3)$ as subtracting $-5$ three times...
Visualizing Negative Times Negative
We may express $0$ as $15$ neutral pairs of blue and red chips.
$0=$





$+$




$+$









$+$





$+$





Visualizing Negative Times Negative
Rearranging we have.






Visualizing Negative Times Negative
Now, "subtract $-5$ a total of $3$" times."
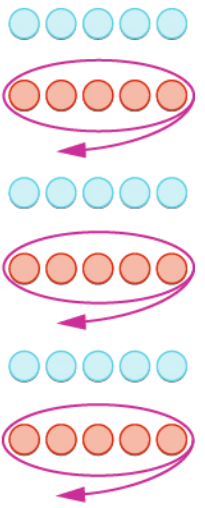
Big Answer: $15$ blue chips!

Negative Times Negative
If you intensely dislike the above demonstration, we can simply prove that $(-5)(-3)$ is $15.$
$$ \begin{array}{lll} (-5)(-3)&=-5(-3)&\mbox{ditch the parentheses on $-5$}\\ &=-(-15)&\mbox{since $5(-3)=-15$ as shown above}\\ &=15&\mbox{$15$ is the opposite of $-15$}\\ \end{array} $$
Summary of Signs
$$(+)(+)=(+)$$ $$(+)(-)=(-)$$ $$(-)(+)=(-)$$ $$(-)(-)=(+)$$
Same signs: positive result.
Opposite signs: negative result.
Example
ⓐ $−9 · 3$
ⓑ $−2(−5)$
ⓒ $4(−8)$
ⓓ $7 · 6$
Solution
ⓐ $−9 · 3=-27$
ⓑ $−2(−5)=10$
ⓒ $4(−8)-32$
ⓓ $7 · 6=42$
Dividing Integers
Dividing Integers follows the same rules for signs.
$$(+)\div(+)=(+)$$ $$(+)\div(-)=(-)$$ $$(-)\div(+)=(-)$$ $$(-)\div(-)=(+)$$
Same signs: positive result.
Opposite signs: negative result.
Example
ⓐ $−27 ÷ 3$
ⓑ $−100 ÷ (−4)$
Solution
ⓐ $−27 ÷ 3=-9$
ⓑ $−100 ÷ (−4)=25$
Expressions Involving Integers
Example $$7(−2) + 4(−7) − 6.$$
Solution $$ \begin{array}{lll} 7(−2) + 4(−7) − 6&= -14+(-28)-6&\mbox{multiply/divide}\\ &= -42-6&\mbox{add/subtract from left to right}\\ &= -48&\mbox{}\\ \end{array} $$
Expressions Involving Integers
Example
ⓐ $(−2)^4$
ⓑ $−2^4$
Solution
ⓐ $$ \begin{array}{lll} (−2)^4&= (-2)(-2)(-2)(-2)&\mbox{four copies of $-2$}\\ &= \underbrace{(-2)(-2)}\underbrace{(-2)(-2)}&\mbox{grouping pairs}\\ &= 4\cdot 4&\mbox{}\\ &= 16&\mbox{}\\ \end{array} $$
ⓑ We note that $-2^4$ is the opposite of $2^4.$ That is, $$ \begin{array}{lll} −2^4&= -2\cdot 2\cdot 2\cdot 2&\mbox{the opposite of four copies of $2$}\\ &= -4\cdot 4&\mbox{}\\ &= -16&\mbox{}\\ \end{array} $$
Expressions Involving Integers
Example
ⓐ $12 − 3(9 − 12)$
ⓑ $8(−9) ÷ (−2)^3$
ⓒ $−30 ÷ 2 + (−3)(−7)$
Solution
ⓐ $$ \begin{array}{lll} 12 − 3(9 − 12)&=12 − 3(-3) &\mbox{Parentheses/Exponents}\\ &=12 − (-9) &\mbox{Multiplication/Division}\\ &=12+9 &\mbox{Subtraction is the addition of opposites!}\\ &=21 &\mbox{Addition/Subtraction}\\ \end{array} $$
ⓑ $$ \begin{array}{lll} 8(−9) ÷ (−2)^3&=8(−9) ÷ (-8) &\mbox{Parentheses/Exponents $(-2)^3=(-2)(-2)(-2)=4(-2)=-8$}\\ &=-72 ÷ (-8) &\mbox{Multiplication/Division}\\ &=9 &\mbox{Multiplication/Division}\\ \end{array} $$
ⓒ $$ \begin{array}{lll} −30 ÷ 2 + (−3)(−7)&=−15+ (−3)(−7) &\mbox{Multiplication/Division from left to right}\\ &=−15+ 21 &\mbox{Multiplication/Division}\\ &6 &\mbox{Multiplication/Division}\\ \end{array} $$
Evaluating Integer Expressions
ⓐ For $n = −5,$ evaluate: $n + 1$ and $−n + 1.$
ⓑ Evaluate $(x + y)^2$ when $x = −18$ and $y = 24$
ⓒ Evaluate $20 − z$ when $z = −12.$
ⓓ $2x^2 + 3x + 8$ when $x = 4.$
Solution
ⓐ $$ \begin{array}{lll} n+1 &= -5+1&\mbox{since $n=-5$}\\ &=-4&\\ \end{array} $$ and $$ \begin{array}{lll} -n+1&=-(-5)+1 &\mbox{since $n=-5$}\\ &=5+1&\\ &=6&\\ \end{array} $$
ⓑ $$ \begin{array}{lll} (x + y)^2&=(-18+24)^2 &\mbox{since $x = −18$ and $y = 24$}\\ &=(6)^2 &\mbox{}\\ &=36 &\mbox{}\\ \end{array} $$
ⓒ $$ \begin{array}{lll} 20 − z&=20-(-12) &\mbox{since $z = −12$}\\ &=20+12 &\mbox{Subtraction is the addition of opposites!}\\ \end{array} $$
ⓓ $$ \begin{array}{lll} 2x^2 + 3x + 8&=2\cdot 4^2 + 3\cdot 4 + 8 &\mbox{since $x=4$}\\ &=2\cdot 16 + 12 + 8 &\mbox{}\\ &=32+20 &\mbox{}\\ &=52 &\mbox{}\\ \end{array} $$
Translation Practice!
We now reinforce the translation skills we have developed...
Warm Up
Translate and simplify:
ⓐ the sum of $8$ and $−12,$ increased by $3$
ⓑ the difference of $13$ and $−21$
ⓒ the product of $−2$ and $14$
ⓓ the quotient of $-56$ and $−7.$
Solution
ⓐ $[8+(−12)]+3=[-4]+3=-1$
ⓑ $13-(−21)=13+21=34$
ⓒ $−2\cdot 14=-28$
ⓓ $-56\div −7=8$
Example
The temperature in Urbana, Illinois one morning was $11$ degrees. By mid-afternoon, the temperature had dropped to $−9$ degrees.
What was the difference of the morning and afternoon temperatures?
Solution
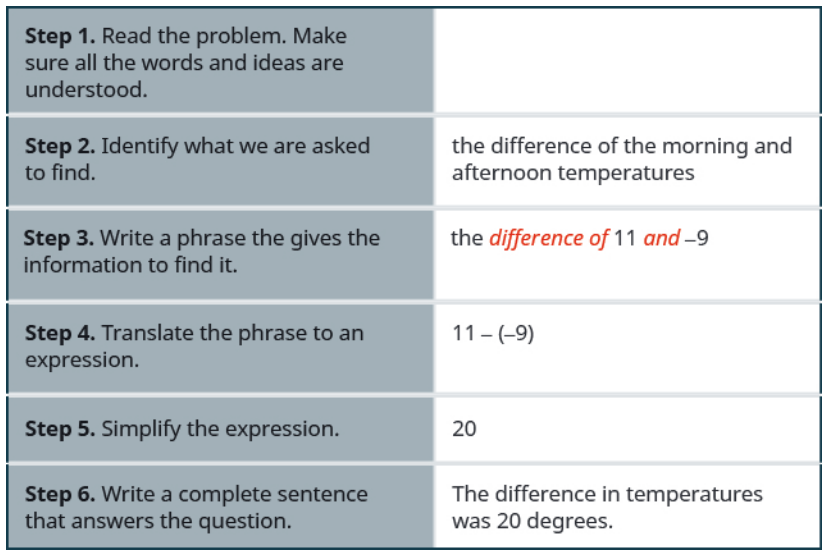
Example
The Mustangs football team received three penalties in the third quarter. Each penalty gave them a loss of fifteen yards. What is the number of yards lost?
Solution
The Mustangs football team received three penalties in the third quarter. Each penalty gave them a loss of fifteen yards. What is the number of yards lost?
| Step 1. Read the problem. Make sure all the words and ideas are understood. | ||
| Step 2. Identify what we are asked to find. | the number of yards lost | |
| Step 3. Write a phrase that gives the information to find it. | three $15$-yard penalties | |
| Step 4. Translate the phrase to an expression. | $3(−15)$ | |
| Step 5. Simplify the expression. | $−45$ | |
| Step 6. Answer the question with a complete sentence. | The team lost $45$ yards. |