Today we expand our universe of numbers from the whole numbers to the integers.
Integers models situations where there's some notion of "above" and "below".
For example, a positive bank balance versus a negative bank balance (owes money).
The Integers
The integers is the collection of numbers $$ \ldots,-5,-4,-3,-2,-1,0,1,2,3,4,5,\ldots $$
The Integers
We visualize the integers as lying on a number line.
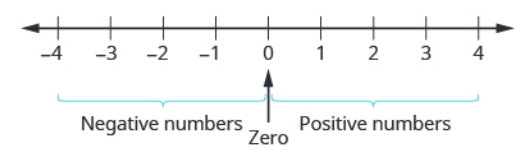
Integers are required to model anything can fall above or below some point of reference.
For example:
- A Bank Balance.
- Profit
- Temperature
- Elevation Above Sea Level
The Integers
The further to the right on the number line, the larger the integer.
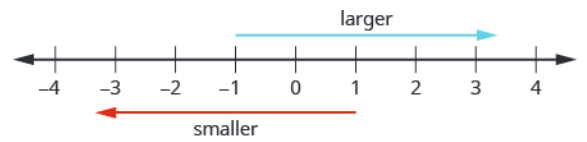
For example, $4 \gt 1$ since $4$ lies to the right of $1.$
Similarly, $1 \lt 4$ since $1$ lies to the left of $4.$
Your Turn: Which is bigger, $-4$ or $-1?$
Example
Order each of the following pairs of numbers, using $\lt$ or $\gt.$
ⓐ $14$___$6$
ⓑ $-1$___$9$
ⓒ $-1$___$-4$
ⓓ $2$___$-20$
Solution
Order each of the following pairs of numbers, using $\lt$ or $\gt.$
ⓐ $14\gt 6$
ⓑ $-1\lt 9$
ⓒ $-1\gt-4$
ⓓ $2\gt-20$
Opposites
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
For example, $-3$ is the opposite of $3.$ Translation: $-3=-3$
Also, $3$ is the opposite of $-3.$ Translation: $3=-(-3)$
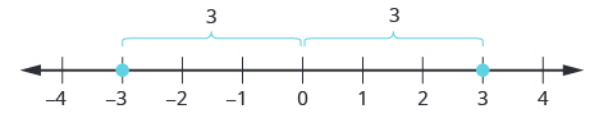
Taking the opposite is finding the reflection about $0.$
Example
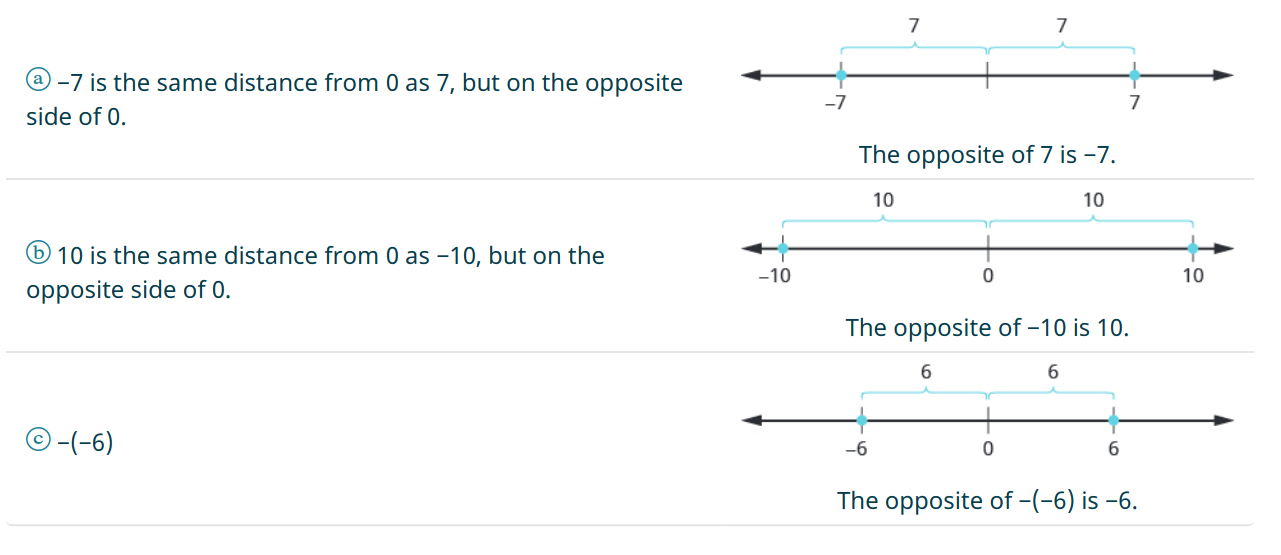
Find the following.
ⓐ the opposite of $7$
ⓑ the opposite of $-10$
ⓒ $-(-6)$
Solution
Working with Expressions
Evaluate the following expressions involving integers.
ⓐ $-x,$ when $x = 8$
ⓑ $-z,$ when $z = -8$
Solution
$$ \begin{array}{lll} -x&=-(8) &\mbox{ since $x=8$}\\ &=-8 &\mbox{since $-8$ is the opposite of $8$}\\ \end{array} $$
$$ \begin{array}{lll} -z&=-(-8) &\mbox{ since $z=-8$}\\ &=8 &\mbox{since $8$ is the opposite of $-8$}\\ \end{array} $$
Absolute Value
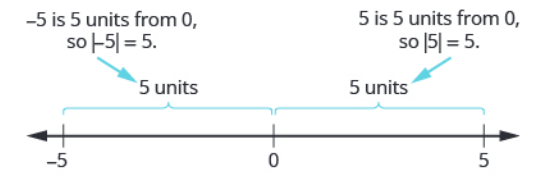
The absolute value of a number $x$ is its distance from $0$ on the number line.
The absolute value of $x$ is written as $|x|.$
For example, $|-5|=5$ since $-5$ is $5$ units away from $0$ on the number line.
Big Fact
Since absolute value is distance from $0,$ it is never negative.
That is, for any $x,$ we have that $|x|\geq 0.$
Example
Simplify the following.
ⓐ $|3|$
ⓑ $|-44|$
ⓒ $|0|$
Solution
Simplify the following.
ⓐ $|3|=3$
ⓑ $|-44|=44$
ⓒ $|0|=0$
More Examples!
Fill in $<,$ $>,$ or $=$ for each of the following pairs of numbers.
ⓐ $|-5|$ ___ $ - |-5|$
ⓑ $8$ ___ $- |-8|$
ⓒ $-9$ ___ $- |-9|$
ⓓ $-(-16)$ ___ $- |-16|$
More Solutions!
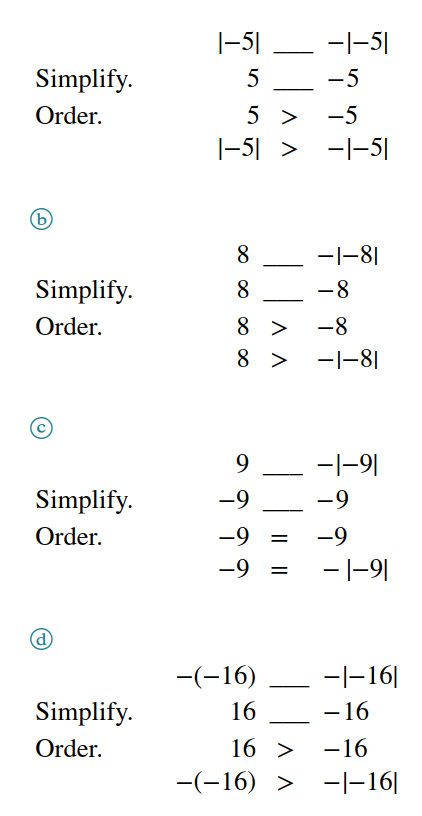
Grouping Symbols Redux
We may now add a fourth grouping symbol to our list. Absolute value!
Parentheses $(\, )$
Brackets $[ \, ]$
Braces $\{ \, \}$
Absolute Value $|\,|$
Example
Simplify the expression. $$24 - |19 - 3(6 - 2)|$$
Solution
$$ \begin{array}{lll} 24 - |19 - 3(6 - 2)|&=24 - |19 - 3(6 - 2)| &\mbox{ }\\ &=24 - |19 - 3(4)| &\mbox{ }\\ &=24 - |19 - 12| &\mbox{ }\\ &=24 - |7| &\mbox{ }\\ &=24 - 7 &\mbox{ }\\ &=17 &\mbox{ }\\ \end{array} $$
Example
Evaluate.
ⓐ $|x|$ when $x = -35$
ⓑ $|-y|$ when $y = -20$
ⓒ $-|u|$ when $u = 12$
ⓓ $-|p|$ when $p = -14$
Solution
ⓐ $|x|$ when $x = -35$ $$ \begin{array}{lll} |x|&=|-35| &\mbox{ since $x=-35$}\\ &=35 &\mbox{}\\ \end{array} $$
ⓑ $|-y|$ when $y = -20$ $$ \begin{array}{lll} |-y|&=|-(-20)| &\mbox{ since $y=-20$}\\ &=|20| &\mbox{ }\\ &=20 &\mbox{ }\\ \end{array} $$
ⓒ $-|u|$ when $u = 12$ $$ \begin{array}{lll} -|u|&=-|12| &\mbox{ since $u=12$}\\ &=-12 &\mbox{}\\ \end{array} $$
ⓓ $-|p|$ when $p = -14$ $$ \begin{array}{lll} -|p|&=-|-14| &\mbox{ since $p=-14$}\\ &=-14 &\mbox{}\\ \end{array} $$
Adding and Subtracting Integers
We now begin performing operations on integers, namely, addition and subtraction
Adding and Subtracting Integers
We shall visualize positive integers as blue chips. For example the integer $5,$ or positive $5$ is represented by $5$ blue chips.
Negative integers will be represented by red chips. So, for example, $-5$ can be visualized as
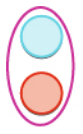
Opposite Pairs
Pairs of opposite integers cancel.
$=0$
If we think of a single blue chip as a dollar in the bank, and a red chip as money we owe, then a blue chip and a red chip together cancel each other out to zero dollars.
Example
Perform the integer addition. $$ -5+3 $$
Solution
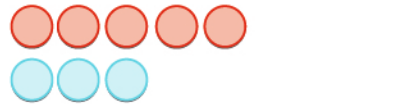Start with $5$ red chips and $3$ blue chips.
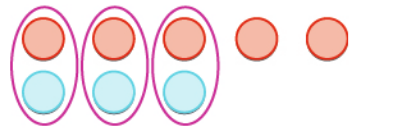$3$ of the blue and red chips cancel out.
We are left with $2$ red chips.
Thus, $$-5+3=-2$$
Example
Perform the integer addition. $$ 5+(-3) $$
Solution
Start with $5$ blue chips and $3$ red chips.
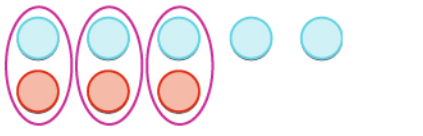$3$ of the blue and red chips cancel out.
We are left with $2$ blue chips.
Thus, $$5+(-3)=2$$
Example
Perform the integer addition.
ⓐ $19 + (-47)$
ⓑ $-14 + (-36)$
Solution
Perform the integer addition.
ⓐ $19 + (-47)=-28$
ⓑ $-14 + (-36)=-50$
Example
Use the order of operations to simplify the following expression.
$-5 + 3(-2 + 7)$
Solution
Use the order of operations to simplify the following expression.
$$ \begin{array}{lll} -5 + 3(-2 + 7)&=-5 + 3(5) &\mbox{}\\ &=-5 + 15 &\mbox{}\\ &=10 &\mbox{}\\ \end{array} $$
Integer Subtraction
Subtraction is the addition of opposites. That is, $$ a-b=a+(-b) $$ So, for example, the subtraction problem $-5-(-3)$ can be simplified in the following way. $$ \begin{array}{lll} -5-(-3)&=-5+[-(-3)]&\mbox{Subtraction is the addition of opposites}\\ &=-5+3&\mbox{since $-(-3)=3$}\\ &=-2&\mbox{}\\ \end{array} $$ Using the blue chip red chip analogy, we can also visualize subtraction...
Integer Subtraction
Begin with 5 red chips: 
Take away $3$ red chips: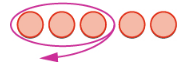 
We are left with $2$ red chips: 
Thus, $$-5-(-3)=-2$$
Example
Subtract.
ⓐ $7 - 5$
ⓑ $-7 - (-5)$
Solution
Subtract.
ⓐ $7 - 5=2$
ⓑ $$ \begin{array}{lll} -7 - (-5)&=-7+[-(-5)]&\mbox{add the opposite of $-5$}\\ &=-7+5&\mbox{in practice, you will likely skip directly to this step}\\ &=-2&\mbox{}\\ \end{array} $$
Integer Subtraction
We now consider the possibility of taking a positive away from a negative.
As an example, we consider the problem $-5-3.$
Again, subtraction is the addition of opposites! $$ \begin{array}{lll} -5-3&=-5+(-3)&\mbox{add the opposite of $3$}\\ &=-8&\mbox{}\\ \end{array} $$ This situation can also be visualized as blue and red chips...
Integer Subtraction
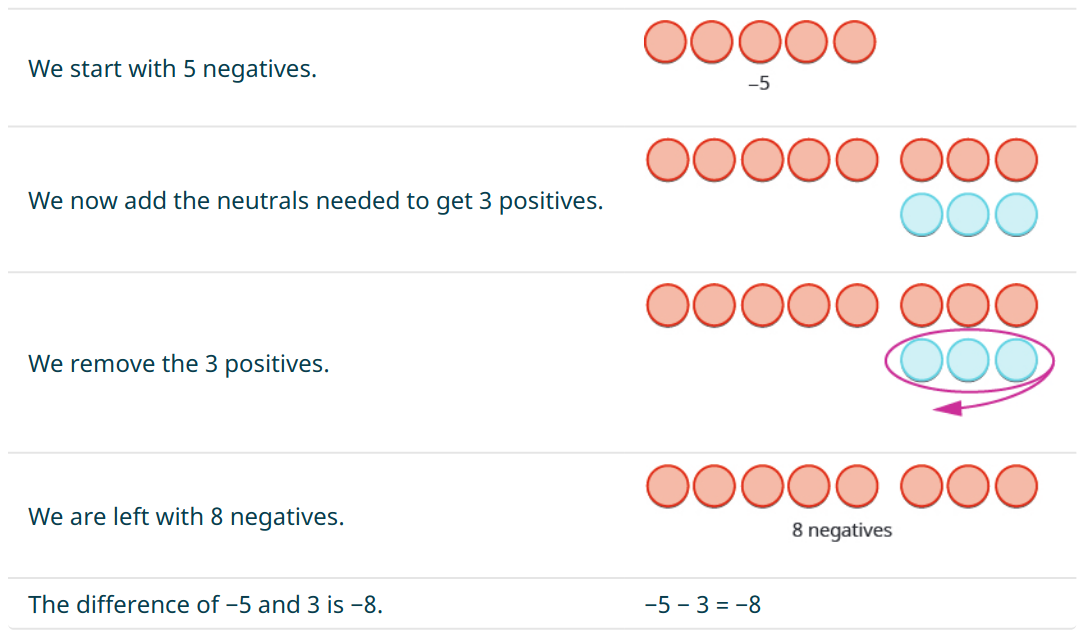
Integer Subtraction
The last possibility we consider is taking a negative away from a positive.
As an example, we consider the problem $5-(-3).$
Again, the familiar refrain subtraction is the addition of opposites echoes through eternity. $$ \begin{array}{lll} 5-(-3)&=5+3&\mbox{add the opposite of $3$}\\ &=8&\mbox{}\\ \end{array} $$ Once again, we'll visualize this scenario as blue and red chips...
Integer Subtraction
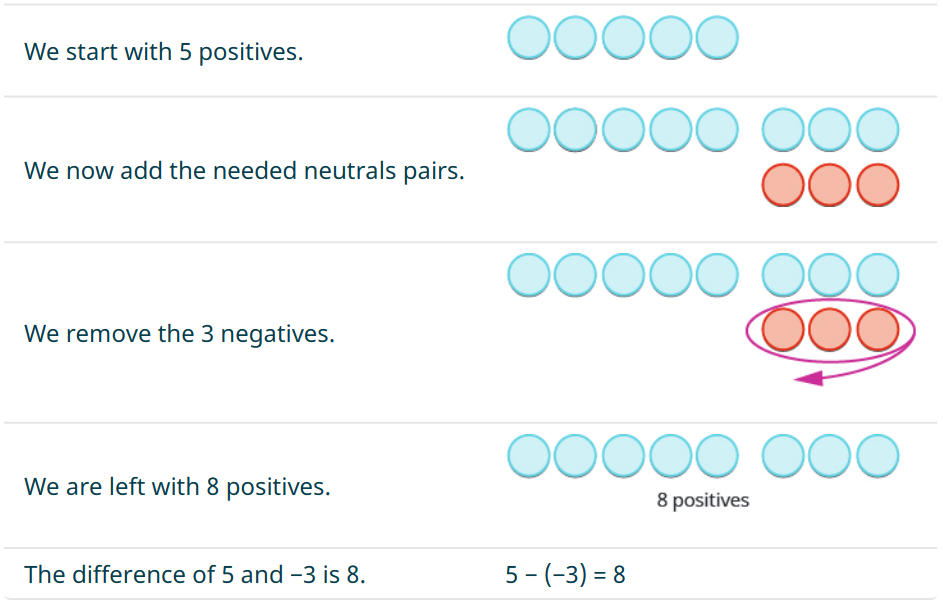
Example
Subtract.
ⓐ $-3 - 1$
ⓑ $3 - (-1)$
Solution
ⓐ $$ \begin{array}{lll} -3 - 1&=-3+(-1)&\mbox{add the opposite of $1$}\\ &=-4&\mbox{}\\ \end{array} $$
Examples
ⓐ $13 + (-8)$
ⓑ $-17 + (-9)$
ⓒ $9 - (-15)$
ⓓ $-7 - (-4)$
Example
And let's not forget that the order of operations always applies! $$ 7 - (-4 - 3) - 9 $$
Solution
And let's not forget that the order of operations always applies! $$ \begin{array}{lll} 7 - (-4 - 3) - 9&=7 - (-7) - 9&\mbox{Parentheses}\\ &=7 + 7 - 9&\mbox{add the opposite of -7}\\ &=14 - 9&\mbox{}\\ &=5&\mbox{}\\ \end{array} $$
Application
The highest elevation in the United States is Mount McKinley (Denali), Alaska, at $\mbox{20,320}$ feet above sea level. The lowest elevation is Death Valley, California, at $282$ feet below sea level at Badwater Basin. Use integers to write the elevation of:
ⓐ Mount McKinley and ⓑ Death Valley.
Write the total elevation gain (change!) from Death Valley to the summit of Mt. McKinley as a difference and evaluate.
Application
ⓐ Mount McKinley: $\mbox{20,320}$ feet (above sea level)
ⓑ Death Valley: $-282$ feet ($282$ below sea level)
Total elevation gain is $\mbox{20,320}-(-282).$ Simplifying this expression, $$ \begin{array}{lll} \mbox{20,320}-(-282)&=\mbox{20,320}+282&\mbox{add the opposite of $-282$}\\ &=20602&\mbox{}\\ \end{array} $$ Thus, the total gain in elevation from Badwater Basin to Denali's summit is $\mbox{20,602}$ feet.