Holt.Blue

The Language of Algebra

The word "algebra" comes from Arabic: ‏الجبر‎ (al-jabr) which roughly means "to put back together."

The word was also used to describe the process of setting broken bones.

There is a good reason why this term applies to what we know today as "algebra"...















































Why Algebra?

When the universe hands us a problem we need to solve, it usually only gives us some of the pieces.

Moreover, these pieces aren't necessarily presented in a nice, neat, and tidy order.

It is our task then to reassemble ("put back together") those pieces into a whole model of the world which makes sense.























Example

Here's a puzzle piece: how did these seashells get to the top of Mt. Diablo which is $\mbox{3,849 ft (1,173 m)}$ above sea level?

























Why Algebra?

Questions such as these lie at the heart of our curiosity and the nature of the universe. Wanting answers is part of what makes us human.

Here are some other fun questions we've asked ourselves at various times in history:

Is the earth actually round? If the earth is a spinning ball, why don't we fall off? What is gravity?

How did we get here? Why are there so many different kinds of creatures? What is life? Does life exist beyond earth?

What is everything made of? Can we turn other substances into gold? How is water different from a rock?

If you can, try to imagine not knowing anything about the above questions.

All you have are puzzle pieces which you are trying to assemble into a model of the universe which answers questions.

























Why Algebra?

Answers to such questions often involve mathematical models.

Let's take our knowledge of the cosmos as an example...

























Humans have been observing the night sky for millennia. What are stars? Why does the sun or moon not fall down on earth? Where does the sun go after dark? The earth looks like it's flat.

























Humans circumnavigate the globe and invent telescopes. Humans figure out the earth isn't flat.

Galileo observed other planets in the solar system including Jupiter and its moons. Humans come to understand that earth orbits the sun and that we're NOT the center of the universe.

























What is the Shape of earth's Orbit?

Kepler, using well-collected astronomical data, formulates three laws of planetary motion. One of which is that all orbits around other planets have the shape of an ellipse. The description of these shapes was made possible by Descartes who linked algebra and geometry by means of a coordinate plane.

























Based upon the pieces Kepler put together, Issac Newton develops a complete model for how celestial bodies move from the three laws of motion formulated in his Principia Mathematica. These laws explain not only the motions of planets, but how objects move on earth. These descriptions required a new kind of mathematics called calculus.

























What is Gravity?

Although Newton's laws gave a good description of gravity, no one knew what gravity actually was. It wasn't until the early $20$th century that Einstein's (and possibly Mileva Marić's) General Theory of Relativity which explains gravity as a warping of space-time by objects with mass.

Relativity explains phenomena which Newton's laws cannot explain and provides a mechanism for these phenomena.



















A Modern Mystery

Our very successful model of the cosmos (General Relativity for big and massive things like planets) does not agree with our very successful model of the very very small (Quantum Mechanics for really small things like atoms, electrons, protons, etc.).

Because of this, we still cannot fully describe things which do exist in the universe like black holes (really small, but super massive).

It's a modern-day mystery we still haven't solved...





















Why Algebra?

Although we will not answer profound questions of our existence and the nature of the universe in this class, we will be assembling the tools you need to make sense, understand, and describe the universe through a mathematical lens.

THIS is what algebra is about.





























Are you ready?



























































Constants versus Variables

Fixed numbers are called constants.

On the other hand, some numbers are always changing, such as:

• your age measured in seconds
• your height
• your weight
• how much gas is left in your tank
• how much money is left in your account
• the population of Oregon
• etc.

Numbers which change (or vary) are called variables. (You see what I did there? ;))

Although variables aren't fixed numbers, we can still give them a name.





















Example

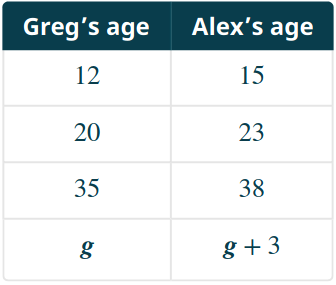
Alex is three years older than Greg.

This fact tells us, for example, that if Greg's age is $12$ years old, then Alex's age is $15.$

In fact, if we let $g$ be Greg's age, then Alex's age is "$3$ more than $g,$" or $g+3.$



















































The Language of Algebra

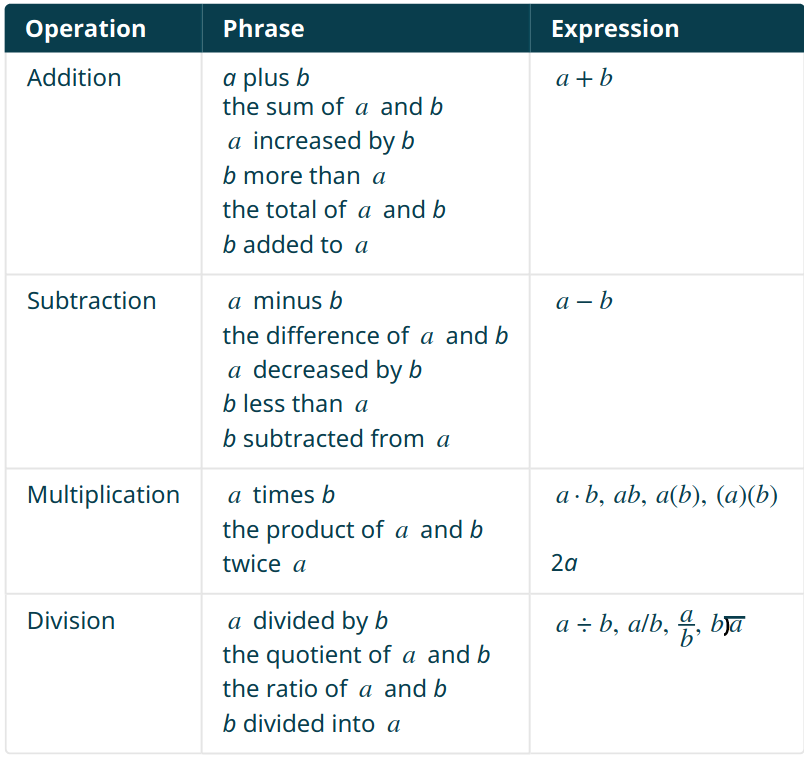
Algebra is a quantitative language which we translate to and from English. Like any language, algebra has its own grammar, syntax and rules. "Expressions" such as $a+b,$ $a-b,$ $a\cdot b,$ $a \div b$ all have translations.


































Expressions

In algebra, an expression is a number, a variable, or a combination of numbers and variables using operations like addition, subtraction, multiplication and division.

Like we saw with variables, expressions can be translated back and forth between algebra and English.



























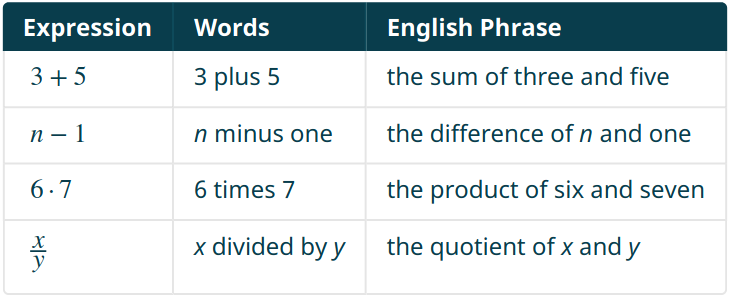
Question: Are any of the above complete sentences?

























Answer



























Another Question: Is the following a complete sentence? $$ \mbox{Alex is three years older than Greg.} $$



























Answer


And using the variable $a$ for Alex's age and $g$ for Greg's age, how could we translate this to the language of algebra?























$$ \updownarrow $$

Notice that "is" is translated to algebra as $=.$

The complete sentence $a=g+3$ is a called an equation.























Equations

An equation is a statement that two expressions are equal.





















How to Form Complete Sentences

In algebra, $=$ is not the only way to form a complete sentence.


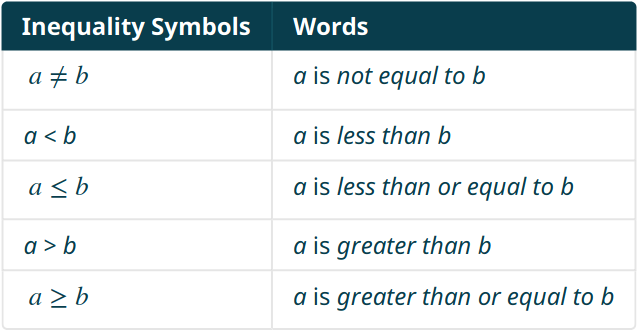
All of the symbols $=, \lt, \gt, \leq, \geq$ express the relative sizes between two quantities.






















Inequalities

An inequality is a statement that one expressions bigger or smaller than the other.


Inequalities can also involve the symbols $\geq$ (greater than or equal) and $\leq$ (less than or equal).
























Translating Inequality Statements

Algebra	English
$17 \leq 26$	$17$ is less than or equal to $26$
$8 \neq 17 - 8$	$8$ is not equal to $8$ less than $17$
$12 \gt 27 \div 3$	$12$ is greater than $27$ divided by $3$
$y + 7 \lt 19$	$7$ more than $y$ is less than $19$

Distinguishing Between Expressions an Equations

Determine if each is an expression or an equation:

	Circle One
ⓐ $2x + 6 = 10$	Equation or Expression
ⓑ $4y - 4 + 1$	Equation or Expression
ⓒ $x \div 25$	Equation or Expression
ⓓ $y + 8 = 40$	Equation or Expression

Examples

Translate the following English phrases into algebra.

"the difference of $17x$ and $5$"

"the quotient of $10x^2$ and $7$"

"Seventeen more than $y$"

"Nine less than $9x^2$"

"five times the sum of $m$ and $n$"

"the sum of five times $m$ and $n$"



























Solutions

Translate the following English phrases into algebra.

"the difference of $17x$ and $5$": $\,\,\,\,17x-5$

"the quotient of $10x^2$ and $7$": $\,\,\,\,10x^2\div 7,$ or $\displaystyle\frac{10x^2}{7}$

"Seventeen more than $y$": $\,\,\,\,y+17$

"Nine less than $9x^2$": $\,\,\,\,9x^2-9$

"five times the sum of $m$ and $n$": $\,\,\,\,5(m+n)$

"the sum of five times $m$ and $n$": $\,\,\,\,5m+n$



























Examples

"The length of a rectangle is $6$ less than the width."

Let $w$ represent the width of the rectangle. Write an expression for the length of the rectangle.





"June has dimes and quarters in her purse. The number of dimes is three less than four times the number of quarters."

Let $q$ represent the number of quarters. Write an expression for the number of dimes.



























Solutions

"The length of a rectangle is $6$ less than the width."

Let $w$ represent the width of the rectangle. Write an expression for the length of the rectangle. $$ w-6 $$



"June has dimes and quarters in her purse. The number of dimes is three less than four times the number of quarters."

Let $q$ represent the number of quarters. Write an expression for the number of dimes. $$ 4q-3 $$





















































































Repeated Operations

Multiplication is nothing more than repeated addition.

For example, $3 \cdot 4$ means $4$ added to itself $3$ times, that is $4+4+4.$



For repeated multiplication there is another notation.

To denote multiplying $4$ by itself $3$ times, that is $4\cdot 4 \cdot 4,$ we may write $4^3.$

In this case, $4$ is called the base and $3$ is called the exponent.























Exponents































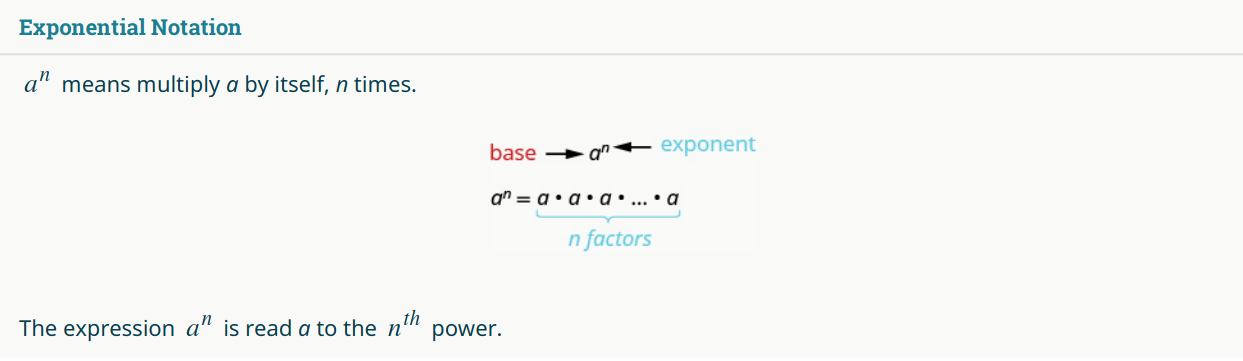
Example

Simplify the expression $3^4.$

























Solution

$$ \begin{array}{lll} 3^4&=3 \cdot 3 \cdot 3 \cdot 3&\mbox{}\\ &=9 \cdot 9&\mbox{}\\ &=81&\mbox{}\\ \end{array} $$























Grouping Symbols

Grouping symbols in algebra are much like the commas, colons, and other punctuation marks in English. They help to make clear which expressions are to be kept together and separate from other expressions.

Three common sets of grouping symbols are:

Parentheses $(\, )$

Brackets $[ \, ]$

Braces $\{ \, \}$

Operations inside these symbols are performed before operations outside these symbols. We'll talk more about this later...

























Order of Operations

Is there any ambiguity to what the expression $2+3\cdot 5$ could equal?

























Order of Operations

Step 1 Start with the expression within the innermost pair of grouping symbols.

Step 2 Perform all exponentiations.

Step 3 Perform all multiplications and divisions as they appear from left to right.

Step 4 Perform all additions and subtractions as they appear from left to right.

















































Examples



Use the order of operations to evaluate $$18 \div 6 + 4(5 - 2)$$

Use the order of operations to evaluate $$5 + 2^3 + 3[6 - 3(4 - 2)]$$



























Solutions

$$ \begin{array}{lll} 18 \div 6 + 4(5 - 2)&=8 \div 6 + 4(3)&\mbox{Parentheses/Exponents}\\ &=3 + 12&\mbox{Multiplication/Division}\\ &=15&\mbox{Addition/Subtraction}\\ \end{array} $$

$$ \begin{array}{lll} 5 + 2^3 + 3[6 - 3(4 - 2)]&=5 + 2^3 + 3[6 - 3(2)]&\mbox{Parentheses/Exponents}\\ &=5 + 2^3 + 3[6 - 6]&\mbox{Parentheses/Exponents}\\ &=5 + 2^3 + 3[0]&\mbox{Parentheses/Exponents}\\ &=5 + 8 + 3[0]&\mbox{Parentheses/Exponents}\\ &=5 + 8 + 0&\mbox{Multiplcation/Division}\\ &=13+0&\mbox{Addition/Subtractions}\\ &=13&\mbox{Addition/Subtractions}\\ \end{array} $$























Evalulating Expressions

Recall that an expression is a number, a variable, or a combination of numbers and variables using operations like addition, subtraction, multiplication and division.

When we evaluate an expression, we substitute numbers in for the variables and evaluate.





























Examples

Find the value of the expression $7x - 4$ if $x=5.$

Evaluate the expression $x^2$ when $x=4.$

Evaluate the expression $3^x$ when $x=4.$

Find the value of the expression $2x^2 + 3x + 8$ when $x=4.$





















Solutions $$ \begin{array}{lll} 7x - 4&=7(5)-4&\mbox{Since $x=5$}\\ &=35-4&\mbox{Multiplication/Division}\\ &=31&\mbox{Addition/Subtraction}\\ \end{array} $$

$$ \begin{array}{lll} x^2&=4^2&\mbox{Since $x=4$}\\ &=4\cdot 4&\mbox{}\\ &=16&\mbox{}\\ \end{array} $$

$$ \begin{array}{lll} 3^x&=3^4&\mbox{Since $x=4$}\\ &=3 \cdot 3 \cdot 3 \cdot 3 &\mbox{}\\ &=9\cdot 9&\mbox{}\\ &=81&\mbox{}\\ \end{array} $$

$$ \begin{array}{lll} 2x^2 + 3x + 8&=2\cdot 4^2 + 3\cdot 4 + 8&\mbox{Since $x=4$}\\ &=2\cdot 16+3\cdot 4+8 &\mbox{Take care of parentheses/exponents.}\\ &=32+12+8 &\mbox{Take care of multiplication/division.}\\ &=44+8 &\mbox{Take care of addition/subtraction.}\\ &=52 &\mbox{Take care of addition/subtraction.}\\ \end{array} $$

























Terms in an Expression: Informal Definition

Loosely speaking, terms are things we add together.

That is to say (very roughly for now!) that the pieces in an expression which are separated by plus signs are terms.

For example, we considered the expression in the above example $$2x^2 + 3x + 8$$ The pieces separated by the plus signs, $2x^2,$ $3x,$ and $8$ are the terms in this expression























Terms in an Expression: Textbook Definition

A term is a constant, or the product of a constant and one or more variables raised to some power.

Examples of terms include $$ \begin{array}{l} 7\\\\ y\\\\ 5x^2\\\\ 9a\\\\ b^5 \end{array} $$ Notice that there are no plus signs in a term. Terms are separated by plus signs.

























Coefficients

In a term, the constant that multiplies the variable(s) is called the coefficient.

Examples include: $$ \begin{array}{ll} 7& \mbox{Coefficient: 7}\\\\ y&\mbox{Coefficient: 1}\\\\ 5x^2&\mbox{Coefficient: 5}\\\\ 9a&\mbox{Coefficient: 9}\\\\ b^5&\mbox{Coefficient: 1} \end{array} $$

























Example

Identify the coefficient of each term.

ⓐ $14y$

ⓑ $15x^2$

ⓒ $a$























Solution

ⓐ $14y,$ coefficient: $14$

ⓑ $15x^2,$ coefficient: $15$

ⓒ $a,$ coefficient: $1$





























Like Terms

Terms which have the same variables and matching exponents are called like terms.

For example $3x^2t^3$ and $7x^2t^3$ are like terms.

On the other hand, both of the following pairs are not like terms. $$ 3x^3t^2, 7x^2t^3\,\,\, \mbox{ Can you say why?} $$ $$ 3y^2t^2, 7x^2t^3\,\,\, \mbox{ Can you say why?} $$

























Example

Identify the like terms: $y^3,$ $7x^2,$ $14,$ $23,$ $4y^3,$ $9x,$ $5x^2.$























Solution



$y^3$ and $4y^3$ are like terms.

$7x^2$ and $5x^2$ are like terms.

$14$ and $23$ are like terms.





















Combining Like Terms

Billy Bob has $3$ $\mbox{Blueberries}$ and $5$ $\mbox{Apples}.$ Linda Lou has $4$ $\mbox{Blueberries}$ and $3$ $\mbox{Apples}.$

Together they have


Notice that it makes sense to combine $\mbox{Blueberries}$ into a single term since they are the same kind of thing. The same is true for $\mbox{Apples}$.

Beyond this, however, we cannot combine the last two terms because $\mbox{Blueberries}$ and $\mbox{Apples}$ are different kinds of things.
























The exact same reasoning applies to like terms!























Combining Like Terms

Billy Bob has $3$ $x^2$'s and $5$ $x$'s. Linda Lou has $4$ $x^2$'s and $3$ $x$'s.

Together they have


Notice that it makes sense to combine $x^2$ into a single term since they are the same kind of thing. (Like terms!) The same is true for $x$.

Beyond this, however, we cannot combine the last two terms because $x^2$ and $x$ are different kinds of things, (i.e., terms!).
























Example

Simplify the expression by combining like terms. $$ 2x^2 + 3x + 7 + x^2 + 4x + 5 $$

























Solution

Simplify the expression by combining like terms.