Although there are many different kinds of numbers, we begin with the the most familiar: the whole numbers.
The Counting Numbers and Whole Numbers
The counting numbers are the numbers we count with: $1,2,3,4,5,6,7,8,\ldots$
The whole numbers are the counting numbers, but $0$ gets to tag along: $0,1,2,3,4,5,6,7,8,\ldots$
We can arrange these numbers on a line like so,

The bigger the number, the further to the right it is on the number line.
Representations of Whole Numbers
There are many ways to represent whole numbers.
For example, notches on a stick.

Representations of Whole Numbers
There are Roman Numerals. The number $1089$ is represented as $$ \mbox{MLXXXIX} $$
The Babylonians would have written $1089$ as


That is, $18\cdot 60+9=1089.$
It turns out that the Babylonians were onto something...
Representations of Whole Numbers
We write $1089$ as $1089$ because
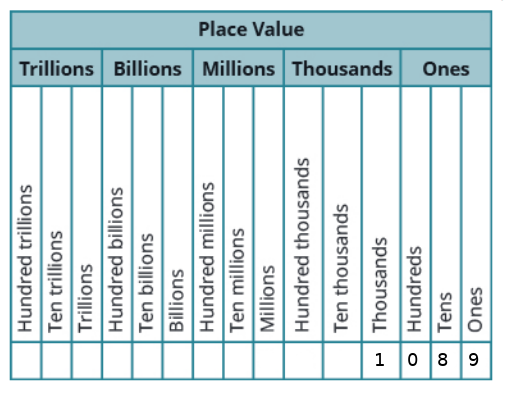
$1089=$ $1$ $\cdot 1000+$ $0$ $\cdot 100+$ $8$ $\cdot 10+$ $9$ $\cdot 1$
The digit $1$ is in the thousands place since there is $1$ copy of $1000$ in $1089.$
The digit $0$ is in the hundreds place since there are $0$ copies of $100$ in $1089.$
The digit $8$ is in the tens place since there are $8$ copies of $10$ in $1089.$
The digit $9$ is in the tens place since there are $9$ copies of $1$ in $1089.$
Fact #1: All whole numbers can be represented in this way.
Fact #2: The Babylonians did the same thing, except instead of $10$'s they used $60$'s.
Representations of Whole Numbers
Example

Solution
Fun Fact
Although we use base $10$ for most numbers, the profound influence of the Babylonian base $60$ system is is still felt today.
For example, there are $360$ degrees in a full rotation.
Another example is time. The time $\mbox{ten forty nine, and 24 seconds}$, or $\mbox{10:49:24},$ means $10$ hours, $49$ minutes, and $24$ seconds. That is,
$\mbox{10:49:24}=$ $10$ $\cdot 3600+$ $49$ $\cdot 60+$ $24$ $\cdot 1$
Naming Numbers
Every number has a name.
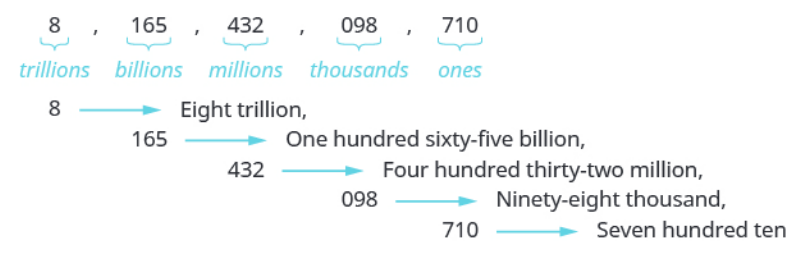
For example, $1089$'s official name is $\mbox{one thousand, eighty nine}.$
$1089$ also has a nickname: "$\mbox{ten eighty nine}$."
Notice that the official name depends on how many ones, tens, hundreds, thousands, etc. are in the number.
Also notice that we omitted the $0$ hundreds part in naming $1089.$
Example
How do we say $\mbox{8,165,432,098,710}$'s name?

Solution
Ballparking Numbers
Sometimes we are only interested in "round" numbers.
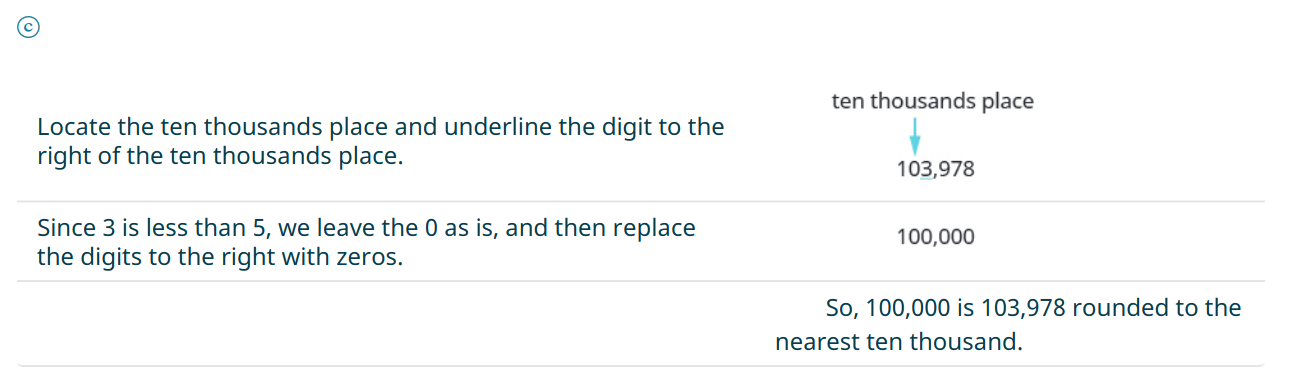
For example we might want to "round out" $1089$ to $1100$ is approximately equal to $1100.$
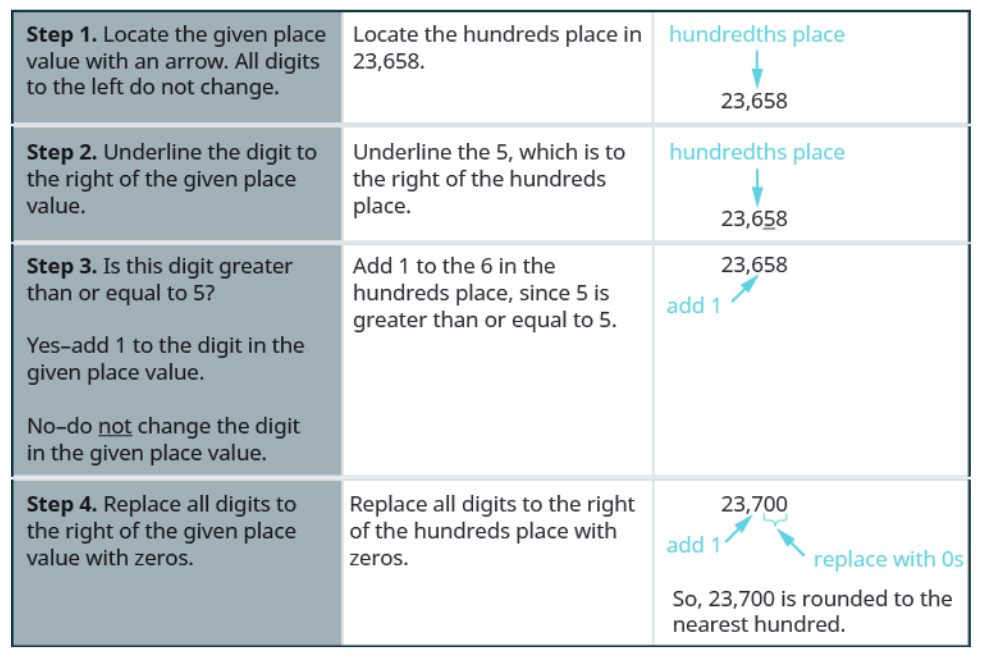
In this case we rounded to the nearest hundred.
Example
Round $\mbox{23,658}$ to the nearest hundred.
Solution
Your Turn

Solution


Multiples and Divisibility of Whole Numbers
A number $n$ it is called a multiple of a number $m$ if $n$ can be written as a product of some number and $m.$
For example, $3, 6, 9, 12, 15, 18, 21,\ldots$ are all multiples of $3.$
$15$ is a multiple of $3$ since $15=5 \cdot 3.$
That is, $15$ is the product of some number and $3.$
Multiples and Divisibility of Whole Numbers
A number $n$ is divisible by number $m$ if $n$ can be written as a product of some number and $m.$
For example, $3, 6, 9, 12, 15, 18, 21,\ldots$ are all divisible by $3.$
$15$ is divisible by $3$ since $15=5 \cdot 3.$
That is, $15$ is the product of some number and $3.$
Did You Notice?
The phrases "is a multiple of" and "is divisible by" both say the same thing!

More Examples of Multiples!

Some of My Favorite Examples
$9801$ is a multiple of $1089.$
$8712$ is a multiple of $2178.$
$2178$ is a multiple of $1089$.
Divisibility Tests
A number is divisible by:
- $2$ if the last digit is $0, 2, 4, 6,$ or $8.$
- $3$ if the sum of the digits is divisible by $3.$
- $5$ if the last digit is $5$ or $0.$
- $6$ if it is divisible by both $2$ and $3.$
- $10$ if it ends with 0.
Is $\mbox{2178}$ divisible by $2?$
Is $\mbox{2178}$ divisible by $3?$
Is $\mbox{2178}$ divisible by $5?$
Is $\mbox{2178}$ divisible by $6?$
Is $\mbox{2178}$ divisible by $10?$
Another Piece of Jargon...
A number $m$ is a factor of $n$ if $n$ is a product of some number and $m.$
For example, $3$ is a factor of $3, 6, 9, 12, 15, 18, 21,\ldots$
$3$ is a factor of $15$ since $15=5 \cdot 3.$
That is, $15$ is the product of some number and $3.$
Wait a Minute...
Isn't this the same thing as a multiple?
Answer
Yes!

The phrases "is a multiple of", "is divisible by" and "is a factor of" all say the same thing!
Factorizations
When we write a number as a product of factors, we say that we have a factorization of that number.
Example $$15=3 \cdot 5$$ That is, $3 \cdot 5$ is a factorization of $15.$
Fact
Some numbers have more factors than others.
For example, $60$ has a lot of factors: $1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30,$ and itself, $60.$
On the other hand $59$ has only two factors: $1$ and $59.$
Numbers which have only $1$ and itself as factors occupy a very special place in the number world.
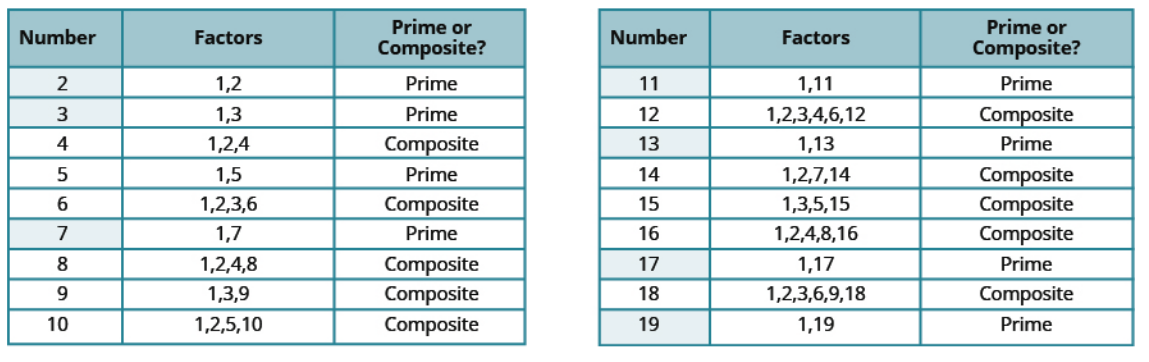
Prime Numbers
Numbers whose only factors are $1$ and itself are called prime numbers.
The prime numbers are $$ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, \ldots $$
Composite Numbers
Numbers which are not prime are called composite numbers.
Prime versus Composite Numbers
Since composite numbers have factors other than $1$ and itself, they can be arranged into rectangles.
On the other hand, primes cannot be arranged into rectangles since their only factors are $1$ and itself.
Prime Factorizations
Fact: Every number has a factorization consisting only of prime numbers.
Example $$60=2 \cdot 3 \cdot 2 \cdot 5$$
Question
Is there a method for finding the prime factorization of a number?
Answer
Yes! Use a factor tree!

Example: Find the prime factorization of $60$ using a factor tree.
Example
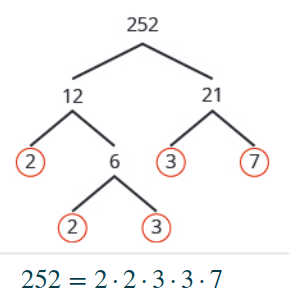
Find the prime factorization of $252.$
Solution
Example
Find the prime factorization of $1089.$
Least Common Multiples
It is a common situation to want to find the smallest number that has two different numbers as multiples.
Such a number is called the least common multiple which we will abbreviate as $\mbox{LCM}.$
For example, we may want to know what the smallest number is which a multiple of both $6$ and $8.$
The simplest way of answering this questions is to write down multiples of $6$ and $8$ and look for the smallest number in both lists.


We see that ________ is the smallest number having $6$ and $8$ as factors.
Least Common Multiples from Prime Factorizations
Another method is to look at the prime factorization of the numbers.
For example, $6=2\cdot 3$ and $8=2 \cdot 2 \cdot 2.$
To find the $\mbox{LCM}$ we play the greedy game.
$6$ is jealous of $8$ because it has three $2$'s. So, the $\mbox{LCM}$ needs three $2$'s.
On the other hand $8$ is jealous of $6$ because it has a $3.$ So, the $\mbox{LCM}$ also needs a $3.$
Then,
$\mbox{LCM}=$ $2 \cdot 2 \cdot 2$ $\cdot \, 3$ $=24$
Example
Find the least common multiple of $24$ and $36.$
Solution
Listing out all the multiples is tedious, so we'll play the greedy game instead.
For example, $24=2\cdot 2 \cdot 2 \cdot 3$ and $36=2 \cdot 2 \cdot 3\cdot 3.$
$24$ is jealous of $36$ because it has two $3$'s. So, the $\mbox{LCM}$ needs two $3$'s.
On the other hand $36$ is jealous of $24$ because it has three $2$'s. So, the $\mbox{LCM}$ also needs three $2$'s.
Then,
$\mbox{LCM}=$ $3 \cdot 3$ $\cdot \, 2 \cdot 2 \cdot 2$$=72$
Application
Billy Bob is throwing a party and will be serving his famous Flamin' Hot Cheeto® hot dogs.

However, Billy Bob is confused and need your help because hot dogs are sold in packages of $10,$ but hot dog buns come in packs of eight.
What is the smallest number that makes the hot dogs and buns come out even?
Help Billy Bob figure out how many packages of each he needs to buy so that every hot dog is paired with a bun?
Solution
Let's look at multiples of $8$ and $10.$



We see that ________ is the smallest number having $8$ and $10$ as factors.
We need to buy ________ packages of hot dogs and ________ packages of buns.
Let's Take This Opportunity to Enjoy Uncertainty
Plot dots at a time.
-1-1
