Today we reap the rewards for learning to solve equations of the form $$ ay''+by'+cy=0 $$ where $a,$ $b,$ and $c$ are constants.
As we have seen already, these equations are important to understanding how current flows in RLC circuits.
Presently, we shall see that they are also important to understanding mechanical vibrations
Special Note
The notation we use here will differ slightly from the book.
There are several places where we have opted to use a more standard notation.
Mass Spring System Model
Consider the mass spring system with a mass $m$ in kilograms attached to a spring with spring constant $k$ newtons per meter and possible force $b$ from sliding friction or the mass being immersed in some medium like a liquid or air.
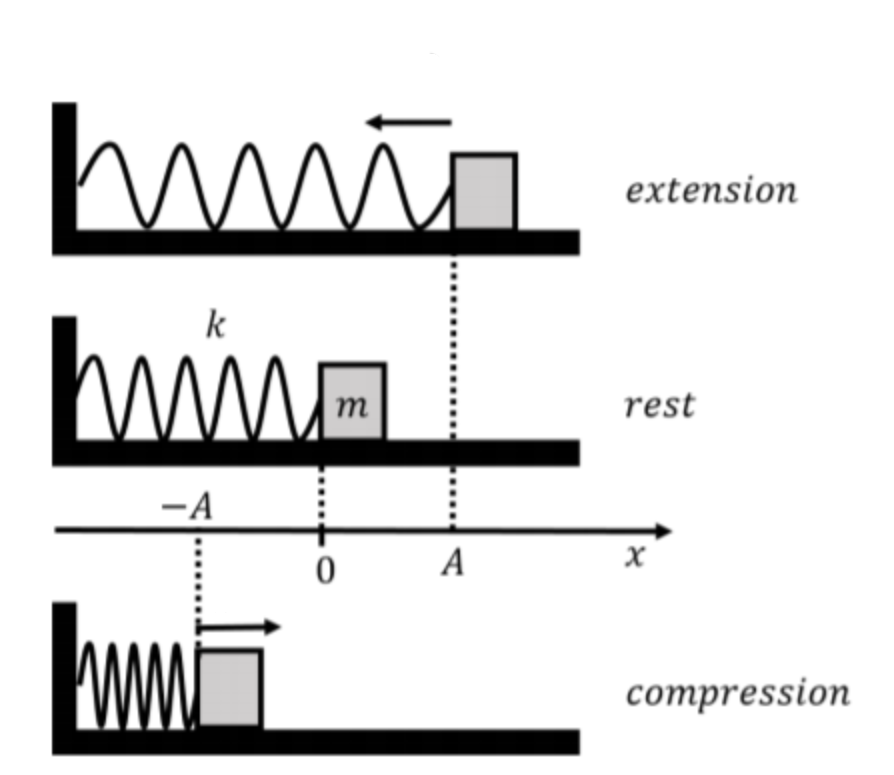
Mass Spring System Model
Consider the mass spring system with a mass $m$ in kilograms attached to a spring with spring constant $k$ newtons per meter and possible force $b$ from sliding friction or the mass being immersed in some medium like a liquid or air.
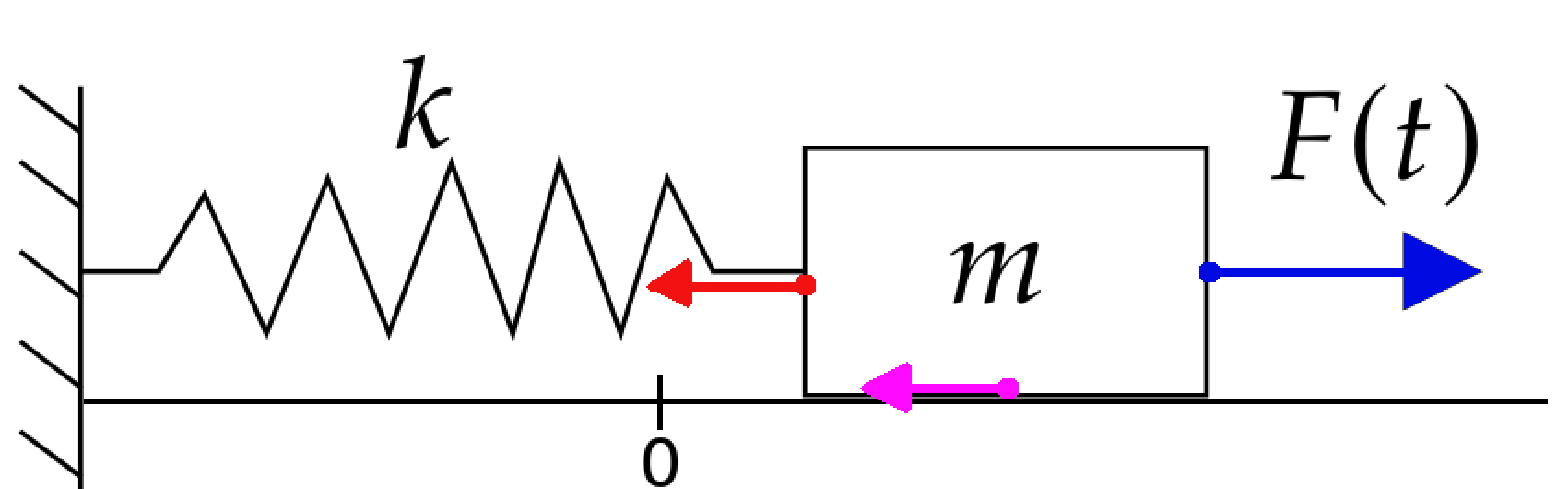
Any other forces on the mass, such as gravity perhaps, we lump into a generic function $F(t).$
Mass Spring System Model
Letting $x$ be the position of the mass at time $t$ with respect to the equilibrium point $0$, we tally up the forces acting on our mass:
Force from spring:$-kx$ by Hooke's Law, $k$ is the spring constant
Force from damping:$-bx',$ the "damping coefficient" is $b$
Other forces: $F(t)$ enables us to account for external forces (like gravity)

Mass Spring System Model
By Newton's Second Law, $ma=F.$
In this situation $a=x''.$ So, $$mx''=ma=\mbox{Net Force on Mass}=\color{magenta}{-bx'}\color{red}{-kx}\color{blue}{+F(t)}$$

Mass Spring System Model
The mass spring system consisting of mass $m$ in kilograms attached to a spring with spring constant $k$ newtons per meter and damping coefficient $c$ is governed by the equation $$ mx''+bx'+kx=F(t) $$ where $F(t)$ is any external force $F(t)$ at time $t.$

Mass Spring System Model with No Forcing
Under no external forces, the mass spring system consisting of mass $m$ in kilograms attached to a spring with spring constant $k$ newtons per meter and damping coefficient $b$ is governed by the equation $$ mx''+bx'+kx=0 $$
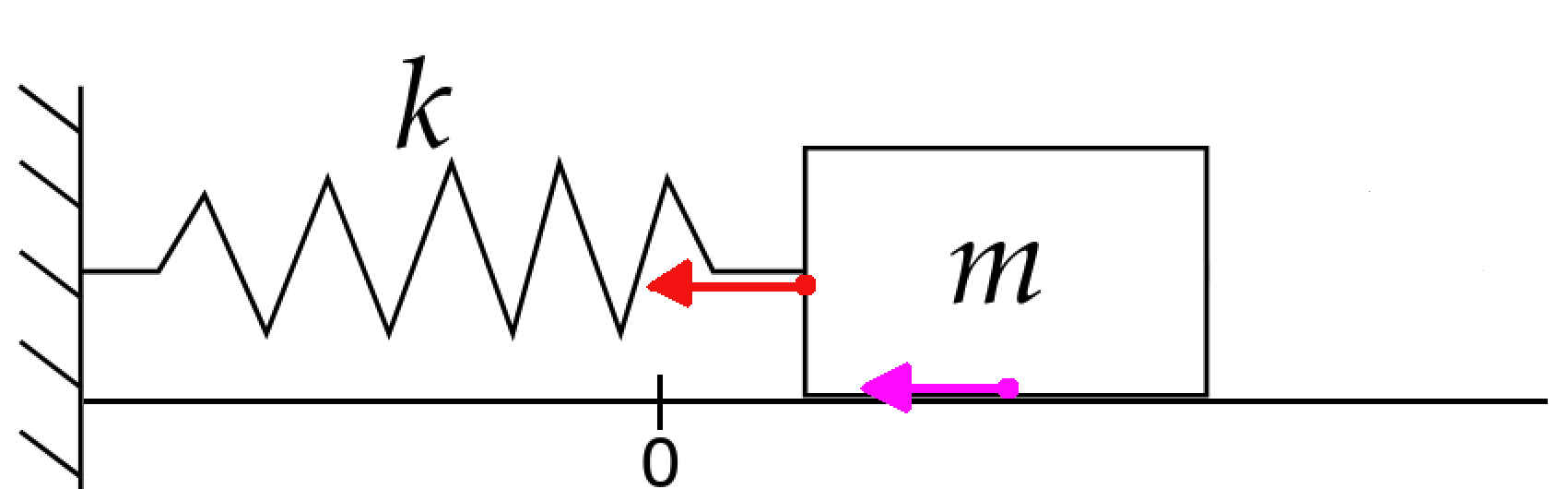
For this section, we will only cover the case with no external forces. That is, free mechanical vibrations with $F(t)=0.$
Part I
Free Undamped Motion
Free Undamped Motion
Free Undamped Motion
With no damping, our mass-spring equation $$ mx''+bx'+kx=0 $$ becomes $$ mx''+kx=0 $$ For reasons soon to be apparent, we shall first divide through by $m$ and rename $\displaystyle \frac{k}{m}$ as $\omega_0^2.$
The above then becomes $$ x''+\omega_0^2x=0 $$ The characteristic equation is $$ r^2+\omega_0^2=0 $$ Thus....
Free Undamped Motion
Since $r=\pm i \omega_0,$ we know that the general solution to the equation describing undamped motion $$ x''+\omega_0^2x=0 $$ is $$ x(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t) $$

Free Undamped Motion
To interpret our results more easily we would like to re-express $$ x(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t) $$ in the form $$ x(t)=A\cos(\omega_0 t-\phi) $$ where $A=\sqrt{C_1^2+C_2^2}$ is the amplitude and $\phi$ is the phase shift.
This free, undamped motion is called simple harmonic motion with angular frequency $\omega_0.$
Important Note #1: The frequency of oscillation in cycles per second is $\displaystyle \frac{\omega_0}{2\pi}.$
Important Note #2: The period of oscillation is $\displaystyle \frac{2\pi}{\omega_0}.$
Free Undamped Motion
Using the cosine difference identity $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=A\cos(\omega_0 t-\phi) &\mbox{}\\ \displaystyle &\displaystyle=A\cos (\omega_0 t) \cos \phi + A\sin (\omega_0 t) \sin \phi &\mbox{}\\ \displaystyle &\displaystyle=A\cos \phi\cos (\omega_0 t) + A\sin \phi \sin (\omega_0 t) &\mbox{}\\ \end{array} $$ Comparing to form $x(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t),$ to the above, we see that $$ C_1=A\cos \phi \,\,\,\,\mbox{and}\,\,\,\,C_2=A\sin \phi $$ Consequently, $$ \tan \phi=\frac{C_2}{C_1} $$
More About Phase Shift
To get $\phi$ in the correct quadrant, we note that the equations from above tell us that the sign of $C_1$ and $\cos \phi$ must agree and the sign of $C_2$ and $\sin \phi$ must agree.
It follows that $$ \begin{array}{lll} C_1\gt 0 \,\,\,\,\mbox{and}\,\,\,\, C_2 \gt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{C_2}{C_1}\right)\,\,\,\,&\mbox{($\phi$ in Quadrant 1)}\\ C_1\lt 0 \,\,\,\,\mbox{and}\,\,\,\, C_2 \gt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{C_2}{C_1}\right)+\pi\,\,\,\,&\mbox{($\phi$ in Quadrant 2)}\\ C_1\lt 0 \,\,\,\,\mbox{and}\,\,\,\, C_2 \lt 0,\,\,\,\, &\displaystyle\phi=\tan^{-1}\left(\frac{C_2}{C_1}\right)+\pi\,\,\,\,&\mbox{($\phi$ in Quadrant 3)}\\ C_1\gt 0 \,\,\,\,\mbox{and}\,\,\,\, C_2 \lt 0,\,\,\,\, &\displaystyle \phi=\tan^{-1}\left(\frac{C_2}{C_1}\right)\,\,\,\,&\mbox{($\phi$ in Quadrant 4)}\\ \end{array} $$
Example
Suppose an undamped mass of $\displaystyle \frac{1}{8}$ kg is attached to a spring with spring constant $k = 16$ N/m.
Furthermore, suppose that when the mass is $0.5$ meters above equilibrium, the mass is moving forward at $\sqrt{2}$ meters per second.
(a) What are the period and frequency of the resulting oscillation?
(b) Find an equation which describes the motion of the mass at time $t.$
(c) What is the amplitude of the resulting oscillation?
(d) What is the phase shift of the resulting oscillation?
(a) Since the motion is undamped, the equation describing the motion is
$\displaystyle \frac{1}{8}x''+16x=0,$ or
$$
x''+128x=0
$$
So, $\omega_0^2=128$ so that $\omega_0=\sqrt{128}=8\sqrt{2}.$
Thus, the period of the oscillation is $$ \frac{2\pi}{\omega_0}=\frac{2\pi}{8\sqrt{2}}=\frac{\pi}{4\sqrt{2}}\approx 0.5553603673\,\, \mbox{seconds} $$ and the frequency is $$ \frac{\omega_0}{2\pi}=\frac{8\sqrt{2}}{2\pi}=\frac{4\sqrt{2}}{\pi}\approx 1.800632632 \,\,\mbox{cycles/second} $$
(b) From the above, the equation of motion is $$ x(t)=C_1\cos(8\sqrt{2} t)+C_2\sin(8\sqrt{2}t) $$ Now, since at the time we begin modelling the motion, "the mass is $0.5$ meters above equilibrium," the initial condition for position is is $x(0)=0.5.$ Then $$ \begin{array}{lll} &\displaystyle C_1\cos(8\sqrt{2} \cdot 0)+C_2\sin(8\sqrt{2}\cdot 0)=0.5&\mbox{}\\ \implies &\displaystyle C_1=0.5&\mbox{}\\ \end{array} $$ At $t=0$ we are also given that, "the mass is moving forward at $\sqrt{2}$ meters per second," so the initial condition for velocity is is $x'(0)=\sqrt{2}.$ That is, $$ \begin{array}{lll} &\displaystyle -C_18\sqrt{2}\sin(8\sqrt{2} \cdot 0)+C_2 8\sqrt{2}\cos(8\sqrt{2}\cdot 0)=\sqrt{2}&\mbox{}\\ \implies &\displaystyle C_2 8\sqrt{2}=\sqrt{2}&\mbox{}\\ \implies &\displaystyle 8C_2=1&\mbox{}\\ \implies &\displaystyle C_2=\frac{1}{8}&\mbox{}\\ \end{array} $$ Our equation of motion is then $$ x(t)=\frac{1}{2}\cos(8\sqrt{2} t)+\frac{1}{8}\sin(8\sqrt{2}t) $$
(c) The amplitude of the oscillation is $$ \begin{array}{lll} \displaystyle A &\displaystyle=\sqrt{C_1^2+C_2^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\left(\frac{1}{2}\right)^2+\left(\frac{1}{8}\right)^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{4}+\frac{1}{64}} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{17}{64}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\sqrt{17}}{8} &\mbox{}\\ \end{array} $$
(d) We now find the phase shift $\phi$ where $\displaystyle \tan \phi=\frac{C_2}{C_1}.$
Since $C_1\gt 0$ and $C_2\gt 0,$ the phase shift $\phi$ is in quadrant $1.$
So, $\displaystyle \phi=\tan^{-1}\left(\frac{1}{4}\right)\approx 0.2449786631,$ and $$ x(t)=A\cos(\omega_0 t-\phi)\approx \frac{\sqrt{17}}{8}\cos(8\sqrt{2}t-0.2449786631) $$ The curve is graphed below.
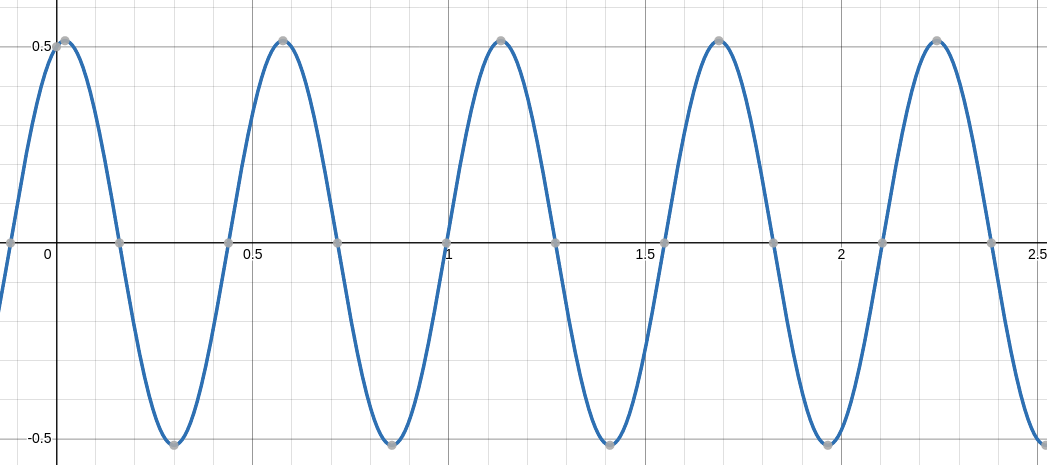
Thus, the period of the oscillation is $$ \frac{2\pi}{\omega_0}=\frac{2\pi}{8\sqrt{2}}=\frac{\pi}{4\sqrt{2}}\approx 0.5553603673\,\, \mbox{seconds} $$ and the frequency is $$ \frac{\omega_0}{2\pi}=\frac{8\sqrt{2}}{2\pi}=\frac{4\sqrt{2}}{\pi}\approx 1.800632632 \,\,\mbox{cycles/second} $$
(b) From the above, the equation of motion is $$ x(t)=C_1\cos(8\sqrt{2} t)+C_2\sin(8\sqrt{2}t) $$ Now, since at the time we begin modelling the motion, "the mass is $0.5$ meters above equilibrium," the initial condition for position is is $x(0)=0.5.$ Then $$ \begin{array}{lll} &\displaystyle C_1\cos(8\sqrt{2} \cdot 0)+C_2\sin(8\sqrt{2}\cdot 0)=0.5&\mbox{}\\ \implies &\displaystyle C_1=0.5&\mbox{}\\ \end{array} $$ At $t=0$ we are also given that, "the mass is moving forward at $\sqrt{2}$ meters per second," so the initial condition for velocity is is $x'(0)=\sqrt{2}.$ That is, $$ \begin{array}{lll} &\displaystyle -C_18\sqrt{2}\sin(8\sqrt{2} \cdot 0)+C_2 8\sqrt{2}\cos(8\sqrt{2}\cdot 0)=\sqrt{2}&\mbox{}\\ \implies &\displaystyle C_2 8\sqrt{2}=\sqrt{2}&\mbox{}\\ \implies &\displaystyle 8C_2=1&\mbox{}\\ \implies &\displaystyle C_2=\frac{1}{8}&\mbox{}\\ \end{array} $$ Our equation of motion is then $$ x(t)=\frac{1}{2}\cos(8\sqrt{2} t)+\frac{1}{8}\sin(8\sqrt{2}t) $$
(c) The amplitude of the oscillation is $$ \begin{array}{lll} \displaystyle A &\displaystyle=\sqrt{C_1^2+C_2^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\left(\frac{1}{2}\right)^2+\left(\frac{1}{8}\right)^2} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{1}{4}+\frac{1}{64}} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{\frac{17}{64}} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\sqrt{17}}{8} &\mbox{}\\ \end{array} $$
(d) We now find the phase shift $\phi$ where $\displaystyle \tan \phi=\frac{C_2}{C_1}.$
Since $C_1\gt 0$ and $C_2\gt 0,$ the phase shift $\phi$ is in quadrant $1.$
So, $\displaystyle \phi=\tan^{-1}\left(\frac{1}{4}\right)\approx 0.2449786631,$ and $$ x(t)=A\cos(\omega_0 t-\phi)\approx \frac{\sqrt{17}}{8}\cos(8\sqrt{2}t-0.2449786631) $$ The curve is graphed below.

Part II
Free Damped Motion
Free Damped Motion
Free (Unforced) Damped Motion
We now consider the situation where friction or other kinds of resistance (damping) are taken into account.
There are three cases to consider:
Over-Damped Motion: too much friction to allow oscillation.
Critically-Damped Motion: the borderline between when no oscillation occurs and when oscillation can occur.
Under-Damped Motion: oscillations occur with decreasing amplitude.
Free (Unforced) Damped Motion
We begin by rewriting our mass-spring equation model $$ mx''+bx'+kx=0 $$ in the form $$ x''+2px'+\omega_0^2x=0 $$ where $\displaystyle \omega_0=\sqrt{\frac{k}{m}}$ and $\displaystyle p=\frac{b}{2m}.$
The characteristic equation is $$ r^2+2pr+\omega_0^2=0 $$ This gives....
Free (Unforced) Damped Motion
$$ \begin{array}{lll} \displaystyle r&\displaystyle= \frac{-2p\pm\sqrt{4p^2-4\omega_0^2}}{2}&\mbox{}\\ \displaystyle &\displaystyle=\frac{-2p\pm2\sqrt{p^2-\omega_0^2}}{2} &\mbox{}\\ \displaystyle &\displaystyle=-p\pm\sqrt{p^2-\omega_0^2} &\mbox{}\\ \end{array} $$ The three cases on our hands are $$ p^2-\omega_0^2\gt 0, \,\,\, p^2-\omega_0^2=0,\,\,\,\mbox{and}\,\,\,p^2-\omega_0^2\lt 0 $$
Free (Unforced) Damped Motion
Since $\displaystyle \omega_0=\sqrt{\frac{k}{m}}$ and $\displaystyle p=\frac{b}{2m},$ the expression $p^2-\omega_0^2$ may be rephrased interms of our original coefficients. $$ \begin{array}{lll} \displaystyle p^2-\omega_0^2&\displaystyle=\left(\frac{b}{2m}\right)^2-\left(\sqrt{\frac{k}{m}}\right)^2 &\mbox{}\\ \displaystyle &\displaystyle=\frac{b^2}{4m^2}-\frac{k}{m} &\mbox{}\\ \displaystyle &\displaystyle=\frac{b^2}{4m^2}-\frac{4km}{4m^2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{b^2-4km}{4m}&\mbox{}\\ \end{array} $$
Free (Unforced) Damped Motion
The three cases mentioned above $$ p^2-\omega_0^2\gt 0, \,\,\, p^2-\omega_0^2=0,\,\,\,\mbox{and}\,\,\,p^2-\omega_0^2\lt 0 $$ become $$ \frac{b^2-4km}{4m}\gt 0, \,\,\, \frac{b^2-4km}{4m}=0,\,\,\,\mbox{and}\,\,\,\frac{b^2-4km}{4m}\lt 0 $$ or, more simply $$ b^2-4km \gt 0\,\,\, b^2-4km=0,\,\,\,\mbox{and}\,\,\,b^2-4km\lt 0 $$
Over-Damped Motion: $b^2-4km \gt 0$
When $b^2-4km \gt 0,$ we know that $p^2-\omega_0^2$ which means that the solutions to the characteristic equation $$ r=-p\pm\sqrt{p^2-\omega_0^2} $$ or $$ r_1=-p+\sqrt{p^2-\omega_0^2}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-\sqrt{p^2-\omega_0^2} $$ are real numbers.
The general solution to the over-damped case is then $$ x(t)=C_1e^{r_1t}+C_2e^{r_2t} $$
Over-Damped Motion: $b^2-4km \gt 0$
With a little thought, it's not difficult to see that $$ r_1=-p+\sqrt{p^2-\omega_0^2}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-\sqrt{p^2-\omega_0^2} $$ are both negative.
It follows that both $e^{r_1 t}$ and $e^{r_2t}$ are decaying exponentials which means that our general solution $$ x(t)=C_1e^{r_1t}+C_2e^{r_2t} $$ goes to $0$ as $t\rightarrow \infty$ and does not oscillate. Is this even a surprise?

Example
Suppose that a $1$-kilogram mass is attached to a spring with a spring constant of $16$ newtons per meter.
The damping coefficient is $\color{magenta}{b=10}$ newtons per meter per second.
Furthermore, at $t=0,$ the spring is released $1$ meter above equilibrium with no initial velocity imparted to it.
Find the equation of motion for this mass.
This mass spring system is governed by the equation
$$
x''+\color{magenta}{10}x+16x=0
$$
with initial conditions $x(0)=1$ and $x'(0)=0.$
Since $b^2-4mk=(10)^2-4(1)(16)=36 \gt 0,$ this is a case of an over-damped system.
The characteristic equation is $$ r^2+10r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-10\pm\sqrt{(10)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm\sqrt{100-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm\sqrt{36}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm 6}{2} &\mbox{}\\ \displaystyle &\displaystyle=-5\pm 3 &\mbox{}\\ \end{array} $$ So, $r=-8$ and $r=-2$ are roots.
It follows that our general solution is $$ x(t)=C_1e^{-2t}+C_2e^{-8t} $$ Thus, we also have $$ x'(t)=-2C_1e^{-2t}-8C_2e^{-8t} $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1+C_2=1\\ -2C_1-8C_2=0\\ \end{cases} $$ Solving this system, $$ C_1=\frac{4}{3}\,\,\,\,\mbox{and}\,\,\,\,C_2=-\frac{1}{3} $$ The equation of motion is then $$ x(t)=\frac{4}{3}e^{-2t}-\frac{1}{3}e^{-8t} $$ The graph of $x(t)$ is seen below.
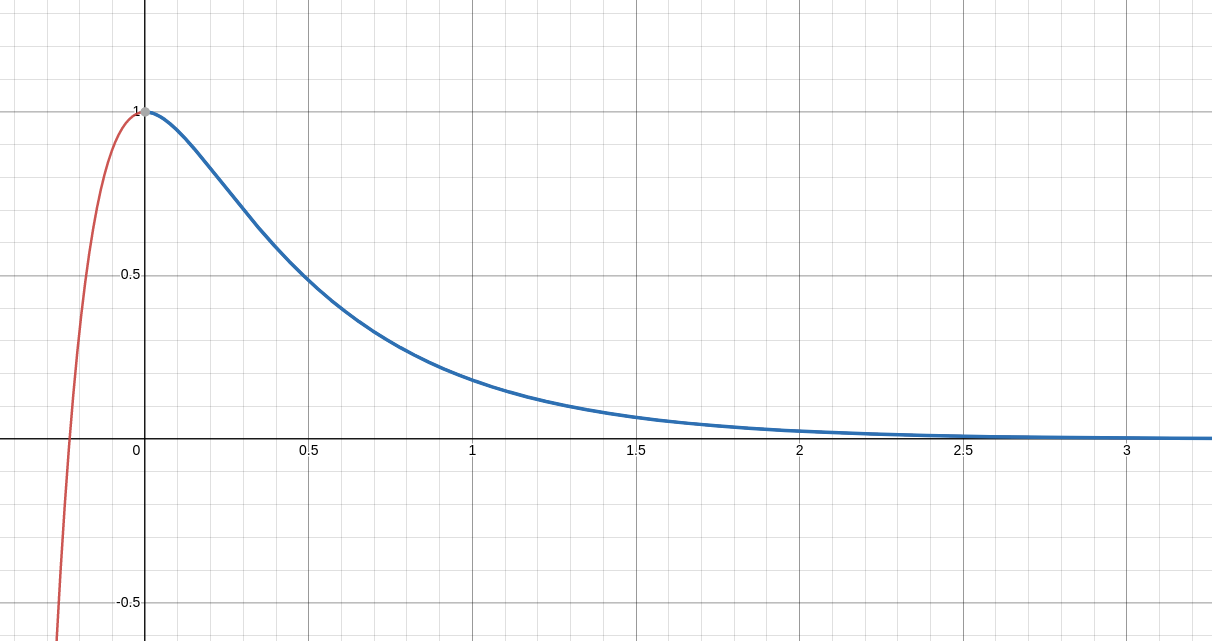
Since $b^2-4mk=(10)^2-4(1)(16)=36 \gt 0,$ this is a case of an over-damped system.
The characteristic equation is $$ r^2+10r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-10\pm\sqrt{(10)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm\sqrt{100-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm\sqrt{36}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-10\pm 6}{2} &\mbox{}\\ \displaystyle &\displaystyle=-5\pm 3 &\mbox{}\\ \end{array} $$ So, $r=-8$ and $r=-2$ are roots.
It follows that our general solution is $$ x(t)=C_1e^{-2t}+C_2e^{-8t} $$ Thus, we also have $$ x'(t)=-2C_1e^{-2t}-8C_2e^{-8t} $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1+C_2=1\\ -2C_1-8C_2=0\\ \end{cases} $$ Solving this system, $$ C_1=\frac{4}{3}\,\,\,\,\mbox{and}\,\,\,\,C_2=-\frac{1}{3} $$ The equation of motion is then $$ x(t)=\frac{4}{3}e^{-2t}-\frac{1}{3}e^{-8t} $$ The graph of $x(t)$ is seen below.

Critically-Damped Motion: $b^2-4km=0$
The critically-damped case is the borderline case between an oscillating and non-oscillating system.
It's the "last stop" before our system begins to oscillate.
Although it is theoretically possible for the equation $b^2-4km=0$ to hold, in practice, if we were to try and tune the parameters of our system to be critically damped, we would never be successful.
The reason is, no matter how hard we try, there will always be some error in our measurements.
The result: any real-world system will be either over-damped or under-damped.
Thus, we won't spend much time with this case.
However,...
Critically-Damped Motion: $b^2-4km=0$
However, we do note that for a critically-damped system, the characteristic equation has a single root $$r=-p$$ so that $$ x(t)=C_1e^{-pt}+C_2te^{-pt} $$ From this solution, we see that the system does not oscillate, and so, in this way it bears some resemblance to the over-damped case.
Example
Suppose that a $1$-kilogram mass is attached to a spring with a spring constant of $16$ newtons per meter.
The damping coefficient is $\color{magenta}{b=8}$ newtons per meter per second.
Furthermore, at $t=0,$ the spring is released $1$ meter above equilibrium with no initial velocity imparted to it.
Find the equation of motion for this mass.
This mass spring system is governed by the equation
$$
x''+\color{magenta}{8}x+16x=0
$$
with initial conditions $x(0)=1$ and $x'(0)=0.$
Since $b^2-4mk=(8)^2-4(1)(16)=0,$ this is a case of a critically-damped system.
The characteristic equation is $$ r^2+8r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-8\pm\sqrt{(8)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8\pm\sqrt{64-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8\pm\sqrt{0}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8}{2} &\mbox{}\\ \displaystyle &\displaystyle=-4 &\mbox{}\\ \end{array} $$ So, $r=-4$ is the only root.
It follows that our general solution is $$ x(t)=C_1e^{-4t}+C_2te^{-4t}=(C_1+C_2t)e^{-4t} $$ Thus, we also have $$ x'(t)=(-4C_2t-4C_1+C_2)e^{-4t} $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -4C_1+C_2=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=4 $$ The equation of motion is then $$ x(t)=(1+4t)e^{-4t} $$ The graph of $x(t)$ is seen below.

Since $b^2-4mk=(8)^2-4(1)(16)=0,$ this is a case of a critically-damped system.
The characteristic equation is $$ r^2+8r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-8\pm\sqrt{(8)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8\pm\sqrt{64-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8\pm\sqrt{0}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-8}{2} &\mbox{}\\ \displaystyle &\displaystyle=-4 &\mbox{}\\ \end{array} $$ So, $r=-4$ is the only root.
It follows that our general solution is $$ x(t)=C_1e^{-4t}+C_2te^{-4t}=(C_1+C_2t)e^{-4t} $$ Thus, we also have $$ x'(t)=(-4C_2t-4C_1+C_2)e^{-4t} $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -4C_1+C_2=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=4 $$ The equation of motion is then $$ x(t)=(1+4t)e^{-4t} $$ The graph of $x(t)$ is seen below.

Under-Damped Motion: $b^2-4km\lt 0$
For the under-damped case, we know that $p^2-\omega_0^2\lt 0$ so that the roots of the characteristic equation $$ r_1=-p+\sqrt{p^2-\omega_0^2}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-\sqrt{p^2-\omega_0^2} $$ are complex numbers. It follows that $$ r_1=-p+\sqrt{-(\omega_0^2-p^2)}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-\sqrt{-(\omega_0^2-p^2)} $$
Under-Damped Motion: $b^2-4km\lt 0$
From the above it follows that $$ r_1=-p+i\sqrt{\omega_0^2-p^2}\,\,\,\,\mbox{and}\,\,\,\,r_2=-p-i\sqrt{\omega_0^2-p^2} $$ Letting $\omega_1=\sqrt{\omega_0^2-p^2},$ the solution to the under-damped case is $$ x(t)=e^{-pt}[C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)] $$

Example
Suppose that a $1$-kilogram mass is attached to a spring with a spring constant of $16$ newtons per meter.
The damping coefficient is $\color{magenta}{b=6}$ newtons per meter per second.
Furthermore, at $t=0,$ the spring is released $1$ meter above equilibrium with no initial velocity imparted to it.
Find the equation of motion for this mass.
This mass spring system is governed by the equation
$$
x''+\color{magenta}{6}x+16x=0
$$
with initial conditions $x(0)=1$ and $x'(0)=0.$
Since $b^2-4mk=(6)^2-4(1)(16)=36-64=-28\lt 0,$ this is a case of an under-damped system.
The characteristic equation is $$ r^2+6r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-6\pm\sqrt{(6)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{36-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{-28}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2\sqrt{-7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2i\sqrt{7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=-3 \pm i\sqrt{7} &\mbox{}\\ \end{array} $$ So, we have complex conjugate roots $-3 \pm i\sqrt{7}.$
It follows that our general solution is $$ x(t)=C_1e^{-3t}\cos(\sqrt{7}t)+C_2e^{-3t}\sin(\sqrt{7}t) $$ Thus, we also have $$ x'(t)=(-3C_1+C_2\sqrt{7})e^{-3t}\cos(\sqrt{7}t)+(-C_1\sqrt{7}-3C_2)e^{-3t}\sin(\sqrt{7}t) $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -3C_1+C_2\sqrt{7}=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=\frac{3}{\sqrt{7}} $$ The equation of motion is then $$ x(t)=e^{-3t}\cos(\sqrt{7}t)+\frac{3}{\sqrt{7}}e^{-3t}\sin(\sqrt{7}t) $$ The graph of $x(t)$ is seen below.
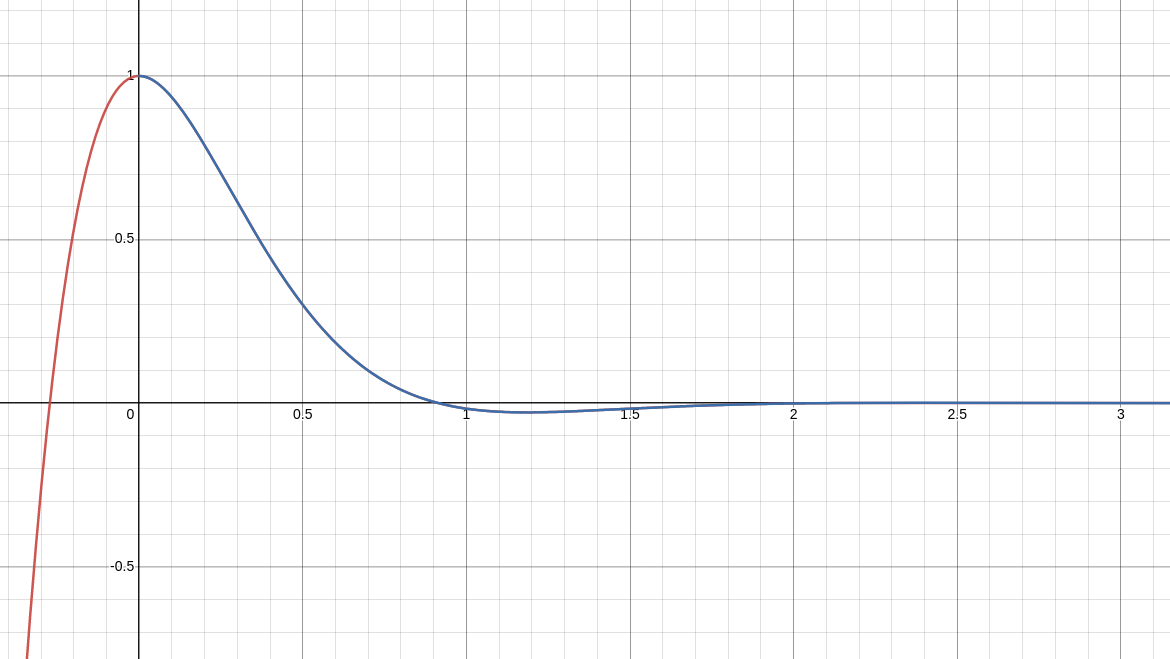
Since $b^2-4mk=(6)^2-4(1)(16)=36-64=-28\lt 0,$ this is a case of an under-damped system.
The characteristic equation is $$ r^2+6r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-6\pm\sqrt{(6)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{36-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{-28}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2\sqrt{-7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2i\sqrt{7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=-3 \pm i\sqrt{7} &\mbox{}\\ \end{array} $$ So, we have complex conjugate roots $-3 \pm i\sqrt{7}.$
It follows that our general solution is $$ x(t)=C_1e^{-3t}\cos(\sqrt{7}t)+C_2e^{-3t}\sin(\sqrt{7}t) $$ Thus, we also have $$ x'(t)=(-3C_1+C_2\sqrt{7})e^{-3t}\cos(\sqrt{7}t)+(-C_1\sqrt{7}-3C_2)e^{-3t}\sin(\sqrt{7}t) $$ Satisfying the initial conditions, $x(0)=1$ and $x'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -3C_1+C_2\sqrt{7}=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=\frac{3}{\sqrt{7}} $$ The equation of motion is then $$ x(t)=e^{-3t}\cos(\sqrt{7}t)+\frac{3}{\sqrt{7}}e^{-3t}\sin(\sqrt{7}t) $$ The graph of $x(t)$ is seen below.

Some Observations and Highlights
The solution to the under-damped case $x(t)=e^{-pt}[C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)]$ is trapped between two decaying exponentials $Ae^{-pt}$ and $-Ae^{-pt}$ where $A=\sqrt{C_1^2+C_2^2}.$
$\omega_1$ is called an angular pseudo-frequency since $x(t)$ is technically a non-periodic function. That said, the number of oscillations per second is interpreted as a pseudo-frequency $\displaystyle \frac{\omega_1}{2\pi}$ with the time between oscillations given by the pseudo-period $\displaystyle \frac{2\pi}{\omega_1}.$

Some Observations and Highlights
Notice that $b^2$ gets closer to $4km,$ $\omega_0^2$ gets closer to $p^2,$ which means that $\omega_1=\sqrt{\omega_0^2-p^2}$ gets closer to $0,$ and the oscillatory behavior starts to vanish.

Some Observations and Highlights
Also, notice that as damping decreases ($b$ and $p$ both get smaller and smaller) two things start to happen: $e^{-pt}$ gets closer to $1,$ and $\omega_1$ gets closer to $\omega_0.$ That is, the solution $$x(t)=e^{-pt}[C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)]$$ begins to look more and more like simple harmonic oscillation $$ x(t)=C_1\cos(\omega_0 t)+C_2\sin(\omega_0 t) $$

Some Observations and Highlights
In similar fashion to simple harmonic motion, the equation of motion for the under-damped case $$x(t)=e^{-pt}[C_1\cos(\omega_1 t)+C_2\sin(\omega_1 t)]$$ may be written as $$ x(t)=Ae^{-pt}\cos(\omega_1 t-\phi) $$ with phase shift $\phi$ computed as before.
This form makes the envelope curves $Ae^{-pt}$ and $-Ae^{-pt}$ more apparent.

Example
In the above example, we saw an under-damped system whose motion was described by the equation $$ x(t)=e^{-3t}\cos(\sqrt{7}t)+\frac{3}{\sqrt{7}}e^{-3t}\sin(\sqrt{7}t) $$ (a) Find the envelope curves.
(b) Find the phase shift $\phi.$
(c) Write this equation in the form $ x(t)=Ae^{-3t}\cos(\omega_1 t-\phi). $
(d) State the pseudo-frequency and pseudo-period of the damped oscillation.
(a)
$$
\begin{array}{lll}
\displaystyle A&\displaystyle=\sqrt{C_1^2+C_2^2} &\mbox{}\\
\displaystyle &\displaystyle= \sqrt{1^2+\left(\frac{3}{\sqrt{7}}\right)^2}&\mbox{}\\
\displaystyle &\displaystyle= \sqrt{1+\frac{9}{7}}&\mbox{}\\
\displaystyle &\displaystyle= \sqrt{\frac{16}{7}}&\mbox{}\\
\displaystyle &\displaystyle= \frac{4}{\sqrt{7}}&\mbox{}\\
\end{array}
$$
From the above, the envelope curves are $\displaystyle \frac{4}{\sqrt{7}}e^{-pt}$ and $\displaystyle -\frac{4}{\sqrt{7}}e^{-pt}.$
(b) Since $C_1=1\gt 0,$ and $C_2=\displaystyle \frac{3}{\sqrt{7}}\gt 0,$ we know $\phi$ lies in Quadrant 1. So, $$ \begin{array}{lll} \displaystyle \phi&\displaystyle=\tan^{-1}\left(\frac{C_2}{C_1}\right) &\mbox{}\\ \displaystyle &\displaystyle=\tan^{-1}\left(\frac{3/\sqrt{7}}{1}\right) &\mbox{}\\ \displaystyle &\displaystyle=\tan^{-1}\left(\frac{3}{\sqrt{7}}\right) &\mbox{}\\ \displaystyle &\displaystyle\approx 0.848062079 &\mbox{}\\ \end{array} $$ (c) From the above, $$ x(t)=\frac{4}{\sqrt{7}}e^{-3t}\cos(\sqrt{7} t-\phi)\approx \frac{4}{\sqrt{7}}e^{-3t}\cos(\sqrt{7} t-0.848062079) $$ The graph with envelope curves is given below.
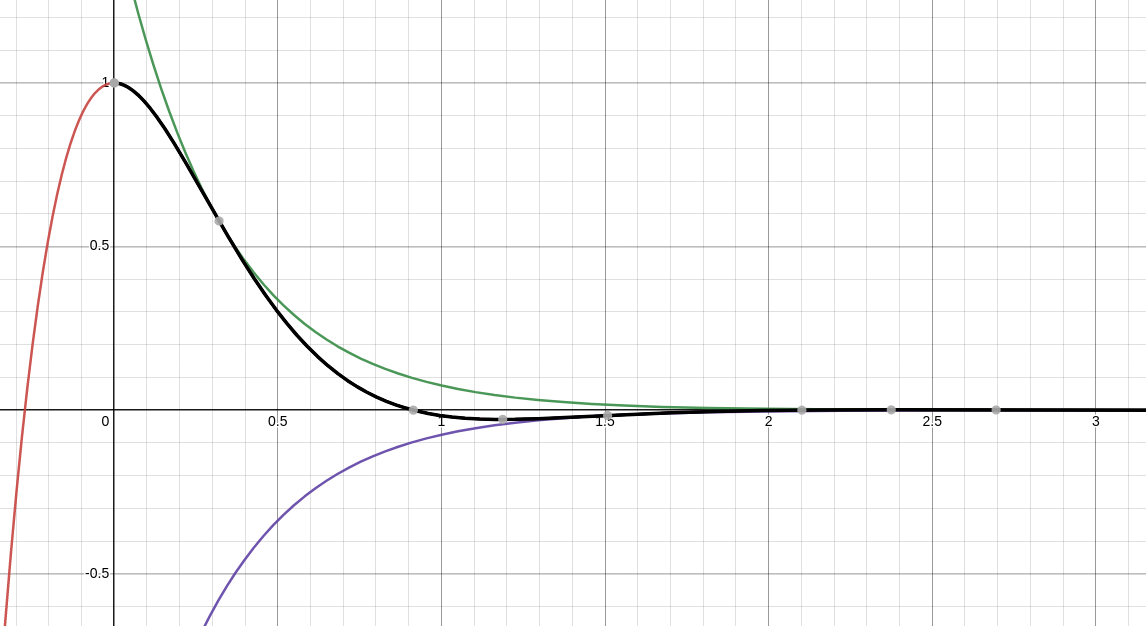
(d) The pseudo-frequency of this oscillation is $$ \frac{\omega_1}{2\pi}=\frac{\sqrt{7}}{2\pi}\approx 0.4210843993\,\, \mbox{ cycles per second} $$ The pseudo-period of this oscillation is $$ \frac{2\pi}{\omega_1}=\frac{2\pi}{\sqrt{7}}\approx 2.374820823\,\, \mbox{seconds} $$
(b) Since $C_1=1\gt 0,$ and $C_2=\displaystyle \frac{3}{\sqrt{7}}\gt 0,$ we know $\phi$ lies in Quadrant 1. So, $$ \begin{array}{lll} \displaystyle \phi&\displaystyle=\tan^{-1}\left(\frac{C_2}{C_1}\right) &\mbox{}\\ \displaystyle &\displaystyle=\tan^{-1}\left(\frac{3/\sqrt{7}}{1}\right) &\mbox{}\\ \displaystyle &\displaystyle=\tan^{-1}\left(\frac{3}{\sqrt{7}}\right) &\mbox{}\\ \displaystyle &\displaystyle\approx 0.848062079 &\mbox{}\\ \end{array} $$ (c) From the above, $$ x(t)=\frac{4}{\sqrt{7}}e^{-3t}\cos(\sqrt{7} t-\phi)\approx \frac{4}{\sqrt{7}}e^{-3t}\cos(\sqrt{7} t-0.848062079) $$ The graph with envelope curves is given below.

(d) The pseudo-frequency of this oscillation is $$ \frac{\omega_1}{2\pi}=\frac{\sqrt{7}}{2\pi}\approx 0.4210843993\,\, \mbox{ cycles per second} $$ The pseudo-period of this oscillation is $$ \frac{2\pi}{\omega_1}=\frac{2\pi}{\sqrt{7}}\approx 2.374820823\,\, \mbox{seconds} $$
Comparing Solutions for Varying $b$
Below are the solutions to the initial value problem $$ x''+bx+16x=0, \,\,\,\, x(0)=1, \,\,\,\, x'(0)=0 $$ for $\color{#ca5451}{b=10}$ (over-damped), $\color{#427fbb}{b=8}$ (critically-damped), and $\color{purple}{b=6}$ (under-damped) are pictured on a single set of axes below for easier comparison.
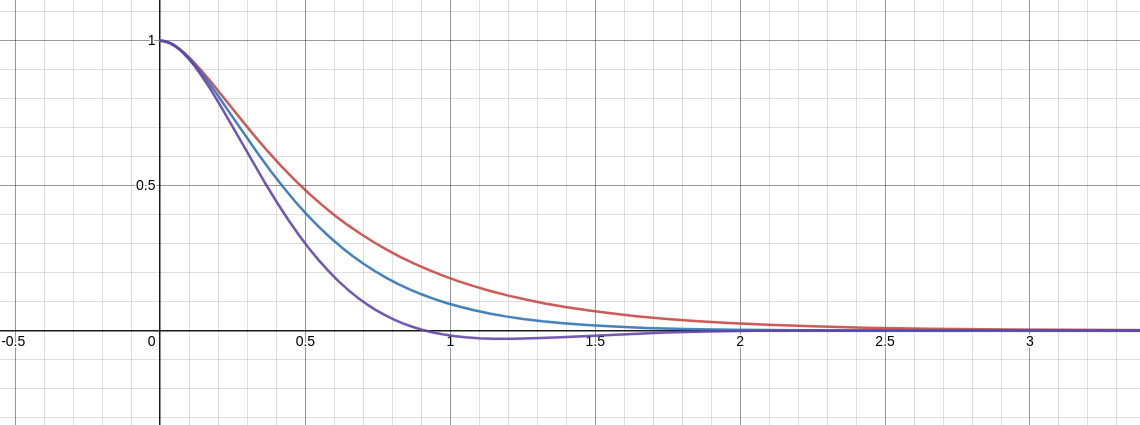
Comparing Solutions for Varying $b$
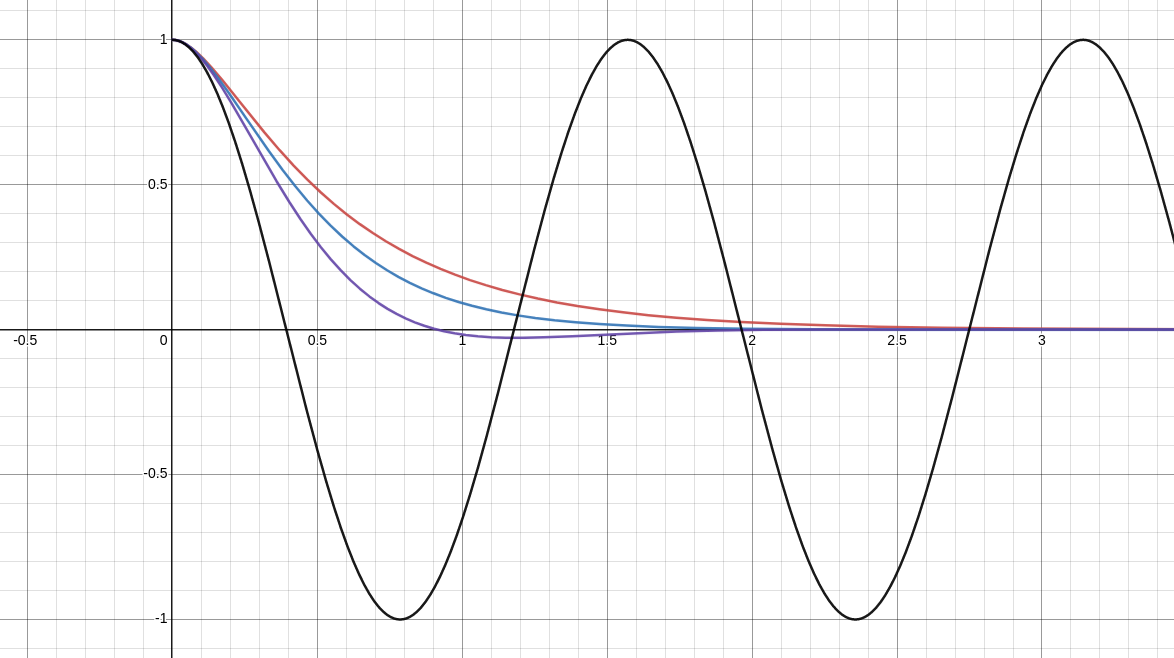
Below are the solutions to the initial value problem $$ x''+bx+16x=0, \,\,\,\, x(0)=1, \,\,\,\, x'(0)=0 $$ for $\color{red}{b=10}$ (over-damped), $\color{blue}{b=8}$ (critically-damped), and $\color{purple}{b=6}$ (under-damped), and $b=0$ (no damping) are pictured on a single set of axes below for easier comparison.
The RLC-Circuit, Mass-Spring Analogy
Since the equations describing mass-spring systems and RLC circuits have the same form, a physical mass-spring system can be used to predict the behavior of an RLC circuit, and vice versa.
For example a mass spring system governed by $x''+6x'+16x=0$ (solved above) can predict the behavior of the circuit whose current is governed by $\displaystyle 0.1I''+0.6I'+\frac{1}{0.625}I=0$ (solved in the last section). They are the equivalent equations!
Mass is analogous to inductance, damping is analogous to resistance, and the spring constant is analogous to the reciprocal of capacitance.
In future sections we will consider mass-spring systems have external forces modelled by a function $F(t).$ This is where we will see forced vibrations and resonance.
In the RLC analogy, $E'(t),$ the rate of change of voltage becomes the forcing function.
An Example Using Non-Metric Units
A mass weighting $40$ lbs stretches a spring $2$ inches.
The mass is in a medium that exerts a viscous resistance of $59$ lbs when the mass has a velocity of $2$ ft/sec.
Suppose the object is displaced an additional $6$ inches and released.
Find an equation for the object's displacement, $x(t),$ in feet after $t$ seconds.
The units we are using for this example are pounds for force, feet for length, and slugs for mass.
Since the mass $40$-pound mass stretches the spring $2$ inches, that is, $\displaystyle \frac{1}{6}$ of a foot, the spring constant is $\displaystyle k=\frac{40}{1/6}=240$ lbs/ft.
The resistance of $59$ lbs at $2$ ft/sec gives our damping coefficient $b=29.5$ lbs per ft/sec.
At standard gravity, taking $1$ slug to be equivalent to $32$ lbf per ft/sec2, the mass of the $40$ lb object in slugs is $\displaystyle m=\frac{40}{32}=\frac{5}{4}$ slug.
The equation to solve is then $$ \frac{5}{4}x''+29.5x'+240x=0 $$ The additional displacement $6$ inches ($0.5$ feet) and release (imparting no initial velocity) is expressed by the initial conditions $$ x(0)=0.5, \,\,\,\,x'(0)=0 $$
Finding our general solution, the characteristic equation is $$ \frac{5}{4}r^2+29.5r+240=0 $$ or $$ 5r^2+118r+960=0 $$ so that $$ \begin{array}{ll} r&=\displaystyle\frac{-118\pm\sqrt{118^2-4(5)(960)}}{2(5)}\\ &=\displaystyle\frac{-118\pm\sqrt{-5276}}{10}\\ &=\displaystyle\frac{-118}{10}\pm\frac{\sqrt{-5276}}{10}\\ &=\displaystyle -11.8\pm i\frac{\sqrt{5276}}{10}\\ &\approx \displaystyle -11.8\pm 7.263607919 i\\ \end{array} $$ The general solution is then $$ x(t)=C_1e^{-11.8t}\cos(7.263607919 t)+C_2e^{-11.8t}\sin(7.263607919 t) $$ Imposing the initial conditions, $$ \begin{array}{lll} &\displaystyle x(0)=0.5 &\mbox{}\\ \implies &\displaystyle C_1e^{-11.8\cdot 0}\cos(7.263607919 \cdot 0)+C_2e^{-11.8\cdot 0}\sin(7.263607919 \cdot 0)=0.5&\mbox{}\\ \implies &\displaystyle C_1=0.5&\mbox{}\\ \end{array} $$ Since $$ x'(t)=-11.8e^{-11.8t}[C_1\cos(7.263607919 t)+C_2\sin(7.263607919 t)]+e^{-11.8t}[-7.263607919C_1\sin(7.263607919 t)+7.263607919 C_2\cos(7.263607919 t)] $$ the second initial condition gives $$ \begin{array}{lll} &\displaystyle x'(0)=0 &\mbox{}\\ \implies &\displaystyle -11.8e^{-11.8 \cdot 0}[C_1\cos(7.263607919 \cdot 0)+C_2\sin(7.263607919 \cdot 0)]+e^{-11.8 \cdot 0}[-7.263607919C_1\sin(7.263607919 \cdot 0)+7.263607919 C_2\cos(7.263607919 \cdot 0)]&\mbox{}\\ \implies &\displaystyle -11.8 C_1+7.263607919 C_2=0&\mbox{}\\ \implies &\displaystyle -11.8\cdot 0.5+7.263607919 C_2=0&\mbox{}\\ \implies &\displaystyle C_2=\frac{11.8\cdot 0.5}{7.263607919}&\mbox{}\\ \implies &\displaystyle C_2 \approx 0.8122685125&\mbox{}\\ \end{array} $$ Our equation of motion is then $$ x(t)=0.5e^{-11.8t}\cos(7.263607919 t)+0.8122685125 e^{-11.8t}\sin(7.263607919 t) $$ The first second of motion is shown by the graph below.

Since the mass $40$-pound mass stretches the spring $2$ inches, that is, $\displaystyle \frac{1}{6}$ of a foot, the spring constant is $\displaystyle k=\frac{40}{1/6}=240$ lbs/ft.
The resistance of $59$ lbs at $2$ ft/sec gives our damping coefficient $b=29.5$ lbs per ft/sec.
At standard gravity, taking $1$ slug to be equivalent to $32$ lbf per ft/sec2, the mass of the $40$ lb object in slugs is $\displaystyle m=\frac{40}{32}=\frac{5}{4}$ slug.
The equation to solve is then $$ \frac{5}{4}x''+29.5x'+240x=0 $$ The additional displacement $6$ inches ($0.5$ feet) and release (imparting no initial velocity) is expressed by the initial conditions $$ x(0)=0.5, \,\,\,\,x'(0)=0 $$
Finding our general solution, the characteristic equation is $$ \frac{5}{4}r^2+29.5r+240=0 $$ or $$ 5r^2+118r+960=0 $$ so that $$ \begin{array}{ll} r&=\displaystyle\frac{-118\pm\sqrt{118^2-4(5)(960)}}{2(5)}\\ &=\displaystyle\frac{-118\pm\sqrt{-5276}}{10}\\ &=\displaystyle\frac{-118}{10}\pm\frac{\sqrt{-5276}}{10}\\ &=\displaystyle -11.8\pm i\frac{\sqrt{5276}}{10}\\ &\approx \displaystyle -11.8\pm 7.263607919 i\\ \end{array} $$ The general solution is then $$ x(t)=C_1e^{-11.8t}\cos(7.263607919 t)+C_2e^{-11.8t}\sin(7.263607919 t) $$ Imposing the initial conditions, $$ \begin{array}{lll} &\displaystyle x(0)=0.5 &\mbox{}\\ \implies &\displaystyle C_1e^{-11.8\cdot 0}\cos(7.263607919 \cdot 0)+C_2e^{-11.8\cdot 0}\sin(7.263607919 \cdot 0)=0.5&\mbox{}\\ \implies &\displaystyle C_1=0.5&\mbox{}\\ \end{array} $$ Since $$ x'(t)=-11.8e^{-11.8t}[C_1\cos(7.263607919 t)+C_2\sin(7.263607919 t)]+e^{-11.8t}[-7.263607919C_1\sin(7.263607919 t)+7.263607919 C_2\cos(7.263607919 t)] $$ the second initial condition gives $$ \begin{array}{lll} &\displaystyle x'(0)=0 &\mbox{}\\ \implies &\displaystyle -11.8e^{-11.8 \cdot 0}[C_1\cos(7.263607919 \cdot 0)+C_2\sin(7.263607919 \cdot 0)]+e^{-11.8 \cdot 0}[-7.263607919C_1\sin(7.263607919 \cdot 0)+7.263607919 C_2\cos(7.263607919 \cdot 0)]&\mbox{}\\ \implies &\displaystyle -11.8 C_1+7.263607919 C_2=0&\mbox{}\\ \implies &\displaystyle -11.8\cdot 0.5+7.263607919 C_2=0&\mbox{}\\ \implies &\displaystyle C_2=\frac{11.8\cdot 0.5}{7.263607919}&\mbox{}\\ \implies &\displaystyle C_2 \approx 0.8122685125&\mbox{}\\ \end{array} $$ Our equation of motion is then $$ x(t)=0.5e^{-11.8t}\cos(7.263607919 t)+0.8122685125 e^{-11.8t}\sin(7.263607919 t) $$ The first second of motion is shown by the graph below.
