Today we learn to solve equations of the form $$ ay''+by'+cy=0 $$ where $a,$ $b,$ and $c$ are constants.
As simple as these equations may be, they are important to understanding mechanical vibrations and RLC circuits.
Recall
Recall finding solutions of the form $e^{rt}$ to the equation $$ y''-15y'+50y=0 $$ We plugged $y=e^{rt}$ into the equation we get $$ \begin{array}{lll} &\displaystyle y''-15y'+50y=0&\mbox{}\\ \implies &\displaystyle (e^{rt})''-15(e^{rt})'+50e^{rt}=0&\mbox{}\\ \implies &\displaystyle (re^{rt})'-15re^{rt}+50e^{rt}=0&\mbox{}\\ \implies &\displaystyle r^2e^{rt}-15re^{rt}+50e^{rt}=0&\mbox{}\\ \implies &\displaystyle (r^2-15r+50)e^{rt}=0&\mbox{}\\ \implies &\displaystyle r^2-15r+50=0&\mbox{since $e^{rt}$ can never be zero}\\ \implies &\displaystyle (r-5)(r-10)=0&\mbox{}\\ \implies &\displaystyle r=5 \,\,\,\mbox{or}\,\,\, r=10&\mbox{}\\ \end{array} $$ We concluded that $e^{5t}$ and $e^{10t}$ are solutions as is easily verified.
Characteristic Equations
We shall now do the same for arbitrary coefficients.
That is, we will assume that we have a solution $y=e^{rx}$ to the equation $$ ay''+by'+cy=0 $$ ...and see what happens!
The Characteristic Equation
If $y=e^{rx},$ then $$ \begin{array}{lll} &\displaystyle ay''+by'+cy=0&\mbox{}\\ \implies &\displaystyle a(e^{rx})''+b(e^{rx})'+ce^{rx}=0&\mbox{}\\ \implies &\displaystyle a r^2 e^{rx}+bre^{rx}+ce^{rx}=0&\mbox{}\\ \implies &\displaystyle (a r^2 +br+c)e^{rx}=0&\mbox{}\\ \end{array} $$ Conclusions??????
The Characteristic Equation
Now, the only way $(a r^2 +br+c)e^{rx}$ could be $0$ for all $x$ is if $$ a r^2 +br+c=0 $$ This equation is called the characteristic equation.
The two roots of this equation $r_1$ and $r_2$ determine the general solution to the equation.
Note: The characteristic equation is sometimes called the auxiliary equation.
The Characteristic Equation
As we know from algebra, we may use the quadratic formula to solve for $r_1$ and $r_2.$ $$ r_1=\frac{-b+\sqrt{b^2-4ac}}{2a}\,\,\,\,\mbox{and}\,\,\,\,r_2=\frac{-b-\sqrt{b^2-4ac}}{2a} $$ From the above, we know that there are three possibilities for $r_1$ and $r_2:$
Case 1: Two distinct real roots. ($b^2-4ac\gt 0$)
Case 2: Two roots which are the same. ($b^2-4ac= 0$) (a.k.a. double root, root of multiplicity $2$)
Case 3: Two complex conjugate roots. ($b^2-4ac\lt 0$)
Case 1: Two Distinct Real Roots
Consider the equation $$ ay''+by'+cy=0 $$ Suppose $r_1$ and $r_2$ are distinct real roots to the characteristic equation.
Then $y_1=e^{r_1 x}$ and $y_2=e^{r_2 x}$ are two linearly independent solutions and $$ y=C_1e^{r_1 x}+C_2e^{r_2 x} $$ is the general solution.
Example
Find the general solution to the equation $$ y''-15y'+50y=0 $$
The characteristic equation for
$$
y''-15y'+50y=0
$$
is
$$
r^2-15r+50=0
$$
The two roots of this equation are $r_1=5$ and $r_2=10.$
Thus, the general solution to the equation is $$ y=C_1e^{5x}+C_2e^{10x} $$
Thus, the general solution to the equation is $$ y=C_1e^{5x}+C_2e^{10x} $$
One Distinct Real Root
Suppose we have the equation $$ y''+4y'+4y=0 $$ The characteristic equation is $$ r^2+4r+4=0 $$ which has two real roots which coincide: $r_1=-2$ and $r_2=-2.$
Thus the characteristic equation gives us one solution, $y_1=e^{-2x}$
One Distinct Real Root
But to find a general solution, we need two linearly independent solutions.
Whatever shall we do?!?!?!?!?!?!?!?!?!?

Case 2: One Distinct Real Root
Consider the equation $$ ay''+by'+cy=0 $$ Suppose $r_1=r$ and $r_2=r$ are double roots (non-distinct roots) of the characteristic equation.
Then $y_1=e^{r x}$ and $y_2=xe^{r x}$ are two linearly independent solutions and $$ y=C_1e^{r x}+C_2 xe^{r x} $$ is the general solution.
We've already shown that $y_1=e^{r x}$ is a solution which induces the characteristic equation $ar^2+br+c=0.$
Since $r_1=r_2=r$ is the only real root, we know that $$ \begin{array}{lll} &\displaystyle r_1=\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{-b-\sqrt{b^2-4ac}}{2a}=r_2&\mbox{}\\ \implies &\displaystyle \sqrt{b^2-4ac}=-\sqrt{b^2-4ac} &\mbox{}\\ \implies &\displaystyle 2\sqrt{b^2-4ac}=0 &\mbox{}\\ \implies &\displaystyle \sqrt{b^2-4ac}=0 &\mbox{}\\ \implies &\displaystyle b^2-4ac=0 &\mbox{}\\ \end{array} $$ Then $$ r=r_1=r_2=\frac{-b\pm 0}{2a}=-\frac{b}{2a} $$ which gives $$ 2ar+b=0 $$ We may now demonstrate that $y_2=xe^{rx}$ is also a solution. $$ \begin{array}{lll} \displaystyle ay_2''+by_2'+cy_2&\displaystyle=a(xe^{rx})''+b(xe^{rx})'+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(e^{rx}+rxe^{rx})'+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(re^{rx}+re^{rx}+r^2xe^{rx})+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(2re^{rx}+r^2xe^{rx})+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=2are^{rx}+xar^2e^{rx}+be^{rx}+xbre^{rx}+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=2are^{rx}+be^{rx}+ar^2xe^{rx}+brxe^{rx}+cxe^{rx} &\mbox{rearrange terms}\\ \displaystyle &\displaystyle=(2ar+b+(ar^2+br+c)x)e^{rx} &\mbox{factoring}\\ \displaystyle &\displaystyle=(0+0\cdot x)e^{rx} &\mbox{}\\ \displaystyle &\displaystyle=0\cdot e^{rx} &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$ We now show that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent.
Suppose that for all $x$ $$ C_1e^{rx}+C_2xe^{rx}=0 $$ Then $$ C_1+C_2x=0 $$ for all $x.$
The only way the above equation could hold for all $x$ is if $C_1=0$ and $C_2=0.$
Thus $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent.
It follows that the general solution to the equation is $$ y=C_1e^{r x}+C_2 xe^{r x} $$
Scenic Alternative
To show that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent we could have used the Wronskian instead. $$ \begin{array}{lll} \displaystyle W[y_1,y_2]&\displaystyle= \left| \begin{array}{cc} y_1 & y_2 \\ y_1'& y_2' \\ \end{array} \right|&\mbox{}\\ \displaystyle &\displaystyle=\left| \begin{array}{cc} e^{r x} & xe^{r x} \\ re^{r x}& e^{rx}+rxe^{r x} \\ \end{array} \right| &\mbox{}\\ \displaystyle &\displaystyle=e^{rx}(e^{rx}+rxe^{r x})-xe^{rx}\cdot re^{rx} &\mbox{}\\ \displaystyle &\displaystyle=e^{2rx}+rxe^{2rx}-rxe^{2rx} &\mbox{}\\ \displaystyle &\displaystyle=e^{2rx} &\mbox{}\\ \displaystyle &\displaystyle\gt 0 &\mbox{}\\ \end{array} $$ Since the Wronskian is nonzero on $(-\infty,\infty),$ we conclude that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent on $(-\infty,\infty).$
Since $r_1=r_2=r$ is the only real root, we know that $$ \begin{array}{lll} &\displaystyle r_1=\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{-b-\sqrt{b^2-4ac}}{2a}=r_2&\mbox{}\\ \implies &\displaystyle \sqrt{b^2-4ac}=-\sqrt{b^2-4ac} &\mbox{}\\ \implies &\displaystyle 2\sqrt{b^2-4ac}=0 &\mbox{}\\ \implies &\displaystyle \sqrt{b^2-4ac}=0 &\mbox{}\\ \implies &\displaystyle b^2-4ac=0 &\mbox{}\\ \end{array} $$ Then $$ r=r_1=r_2=\frac{-b\pm 0}{2a}=-\frac{b}{2a} $$ which gives $$ 2ar+b=0 $$ We may now demonstrate that $y_2=xe^{rx}$ is also a solution. $$ \begin{array}{lll} \displaystyle ay_2''+by_2'+cy_2&\displaystyle=a(xe^{rx})''+b(xe^{rx})'+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(e^{rx}+rxe^{rx})'+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(re^{rx}+re^{rx}+r^2xe^{rx})+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=a(2re^{rx}+r^2xe^{rx})+b(e^{rx}+rxe^{rx})+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=2are^{rx}+xar^2e^{rx}+be^{rx}+xbre^{rx}+cxe^{rx} &\mbox{}\\ \displaystyle &\displaystyle=2are^{rx}+be^{rx}+ar^2xe^{rx}+brxe^{rx}+cxe^{rx} &\mbox{rearrange terms}\\ \displaystyle &\displaystyle=(2ar+b+(ar^2+br+c)x)e^{rx} &\mbox{factoring}\\ \displaystyle &\displaystyle=(0+0\cdot x)e^{rx} &\mbox{}\\ \displaystyle &\displaystyle=0\cdot e^{rx} &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$ We now show that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent.
Suppose that for all $x$ $$ C_1e^{rx}+C_2xe^{rx}=0 $$ Then $$ C_1+C_2x=0 $$ for all $x.$
The only way the above equation could hold for all $x$ is if $C_1=0$ and $C_2=0.$
Thus $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent.
It follows that the general solution to the equation is $$ y=C_1e^{r x}+C_2 xe^{r x} $$
Scenic Alternative
To show that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent we could have used the Wronskian instead. $$ \begin{array}{lll} \displaystyle W[y_1,y_2]&\displaystyle= \left| \begin{array}{cc} y_1 & y_2 \\ y_1'& y_2' \\ \end{array} \right|&\mbox{}\\ \displaystyle &\displaystyle=\left| \begin{array}{cc} e^{r x} & xe^{r x} \\ re^{r x}& e^{rx}+rxe^{r x} \\ \end{array} \right| &\mbox{}\\ \displaystyle &\displaystyle=e^{rx}(e^{rx}+rxe^{r x})-xe^{rx}\cdot re^{rx} &\mbox{}\\ \displaystyle &\displaystyle=e^{2rx}+rxe^{2rx}-rxe^{2rx} &\mbox{}\\ \displaystyle &\displaystyle=e^{2rx} &\mbox{}\\ \displaystyle &\displaystyle\gt 0 &\mbox{}\\ \end{array} $$ Since the Wronskian is nonzero on $(-\infty,\infty),$ we conclude that $y_1=e^{r x}$ and $y_2=xe^{r x}$ are linearly independent on $(-\infty,\infty).$
Example
Find the general solution to $$ y''+4y'+4y=0 $$
The characteristic equation of
$$
y''+4y'+4y=0
$$
is
$$
r^2+4r+4=0
$$
which has two real roots which coincide: $r_1=-2$ and $r_2=-2.$
Then $y_1=e^{-2 x}$ and $y_2=xe^{-2 x}$ are two linearly independent solutions and $$ y=C_1e^{-2 x}+C_2 xe^{-2 x} $$ is the general solution.
Then $y_1=e^{-2 x}$ and $y_2=xe^{-2 x}$ are two linearly independent solutions and $$ y=C_1e^{-2 x}+C_2 xe^{-2 x} $$ is the general solution.
Finding a Second Linearly Independent Solution
We have just seen that sometimes life only hands us a single linearly independent solution to a second-order ODE.
You might be asking yourself, how did we come up with $xe^{rx}$ as a second solution?
One answer is the tried and true method of simply guessing at a simple solution.
However there is a more systematic method...
Reduction of Order
If we assume that $y_1$ is a solution to a general second-order, homogeneous linear equation $$ y''+p(x)y'+q(x)=0 $$ we can find a second linearly independent solution $y_2$ by assuming that $y_2(x)=v(x)y_1(x)$ and plugging it into the above equation.
This results in a linear equation which enables us to solve for $v'(x),$ and hence, a second linearly independent solution.
We put this method off until later. The method is called reduction of order.
Case 3: Two complex conjugate roots.
Consider the equation $$ ay''+by'+cy=0 $$ Suppose $r_1=\alpha + \beta i,$ and $r_2=\alpha - \beta i$ are complex conjugate roots of the characteristic equation.
Then $y_1=e^{\alpha x}\cos(\beta x)$ and $y_2=e^{\alpha x}\sin(\beta x)$ are two linearly independent solutions and $$ y=C_1e^{\alpha x}\cos(\beta x)+C_2 e^{\alpha x}\sin(\beta x) $$ is the general solution.
Example
Find the general solution to $$ y''+2y'+4y=0 $$
The characteristic equation of
$$
y''+2y'+4y=0
$$
is
$$
r^2+2r+4=0
$$
Solving for $r,$
$$
\begin{array}{lll}
\displaystyle r&\displaystyle=\frac{-b+\sqrt{b^2-4ac}}{2a} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-2+\sqrt{2^2-4(1)(4)}}{2(1)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-2+\sqrt{-12}}{2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-2+2\sqrt{-3}}{2} &\mbox{}\\
\displaystyle &\displaystyle=-1+\sqrt{-3} &\mbox{}\\
\displaystyle &\displaystyle=-1+i\sqrt{3} &\mbox{}\\
\end{array}
$$
Thus $y_1=e^{- x}\cos(\sqrt{3} x)$ and $y_2=e^{-x}\sin(\sqrt{3} x)$ are two linearly independent solutions and
$$
y=C_1e^{-x}\cos(\sqrt{3} x)+C_2 e^{-x}\sin(\sqrt{3} x)
$$
is the general solution.
Some Background on Case 3
In the larger world of complex numbers, $y_1=e^{(\alpha + \beta i)x}=e^{\alpha x}e^{i \beta x}$ and $y_2=e^{(\alpha -\beta i)x}=e^{\alpha x} e^{-i\beta x}$ are two linearly independent solutions to the equation $$ ay''+by'+cy=0 $$ so that the general solution is $y=K_1e^{(\alpha + \beta i)x}+K_2e^{(\alpha - \beta i)x}=K_1e^{\alpha x}e^{i\beta x}+K_2e^{\alpha x}e^{-i\beta x}$
However, for the purposes of this course we want real solutions.
Some Background on Case 3
Since the series expansion of $e^{x}$ is $\displaystyle \sum_{n=0}^{\infty}\frac{x^{n}}{n!},$ we substitute $x=i\theta$ into the expansion to get $$ \begin{array}{lll} \displaystyle e^{i\theta} &=\displaystyle \sum_{n=0}^{\infty}\frac{(i\theta)^{n}}{n!}&\mbox{}\\ &=\displaystyle \sum_{n=0}^{\infty}i^{n}\frac{\theta^{n}}{n!}&\mbox{}\\ &=\displaystyle i^{0}\frac{\theta^{0}}{0!}+i^{1}\frac{\theta^{1}}{1!}+i^{2}\frac{\theta^{2}}{2!}+i^{3}\frac{\theta^{3}}{3!}+i^{4}\frac{\theta^{4}}{4!}+i^{5}\frac{\theta^{5}}{5!}+i^{6}\frac{\theta^{6}}{6!}+i^{7}\frac{\theta^{7}}{7!}+\cdots&\mbox{}\\ &=\displaystyle 1+i\theta-\frac{\theta^{2}}{2!}-i\frac{\theta^{3}}{3!}+\frac{\theta^{4}}{4!}+i\frac{\theta^{5}}{5!}-\frac{\theta^{6}}{6!}-i\frac{\theta^{7}}{7!}+\cdots&\mbox{}\\ &=\displaystyle 1-\frac{\theta^{2}}{2!}+\frac{\theta^{4}}{4!}-\frac{\theta^{6}}{6!}+\cdots +i\theta-i\frac{\theta^{3}}{3!}+i\frac{\theta^{5}}{5!}-i\frac{\theta^{7}}{7!}+\cdots&\mbox{}\\ &=\displaystyle 1-\frac{\theta^{2}}{2!}+\frac{\theta^{4}}{4!}-\frac{\theta^{6}}{6!}+\cdots +i\left(\theta-\frac{\theta^{3}}{3!}+\frac{\theta^{5}}{5!}-\frac{\theta^{7}}{7!}+\cdots\right)&\mbox{}\\ &=\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^n\theta^{2n}}{(2n)!}+i\sum_{n=0}^{\infty}\frac{(-1)^n \theta^{2n+1}}{(2n+1)!}&\mbox{}\\ &=\displaystyle \cos \theta +i\sin \theta&\mbox{}\\ \end{array} $$
Some Background on Case 3
From the above we get that $$ \begin{array}{lll} \displaystyle e^{\pm i\beta x}&\displaystyle=\cos (\pm \beta x) +i\sin (\pm\beta x) &\mbox{}\\ \displaystyle &\displaystyle=\cos (\beta x) \pm i\sin (\beta x) &\mbox{}\\ \end{array} $$ so that for our general solution $$ \begin{array}{lll} \displaystyle y&\displaystyle=K_1e^{\alpha x}e^{i\beta x}+K_2e^{\alpha x}e^{-i\beta x} &\mbox{}\\ \displaystyle &\displaystyle=K_1e^{\alpha x}(\cos (\beta x) + i\sin (\beta x))+K_2e^{\alpha x}(\cos (\beta x) - i\sin (\beta x)) &\mbox{}\\ \displaystyle &\displaystyle=(K_1+K_2)e^{\alpha x}\cos (\beta x) + i(K_1-K_2)e^{\alpha x}\sin (\beta x)&\mbox{}\\ \end{array} $$ Stipulating that $K_1$ be a real constant $C_1$ and $K_1-K_2=-iC_2$ where $C_2$ is also a real constant gives the general solution in the real numbers $$ y=C_1e^{\alpha x}\cos (\beta x) + C_2e^{\alpha x}\sin (\beta x) $$
In Summary
To find the general solution $y$ to the second-order linear, constant coefficient, homogeneous equation $$ ay''+by'+cy=0 $$ there are three cases:
Case 1: Two distinct real roots $r_1$ and $r_2$ give $y=C_1e^{r_1 x}+C_2e^{r_2 x}$
Case 2: One distinct real root $r$ gives $y=C_1e^{rx}+C_2xe^{rx}$
Case 3: Two complex conjugate roots $r=\alpha \pm \beta i$ gives $y=C_1e^{\alpha x}\cos (\beta x) + C_2e^{\alpha x}\sin (\beta x)$
Application of Second-Order Linear Constant Coefficient Equations: RLC Circuits
The equation which describes the flow of current $I$ in an RLC circuit is $$ LI''+RI'+\frac{1}{C}I=E'(t) $$ where $L\gt 0$ is the inductance (in henries), $R\gt 0$ is the resistance (in ohms), $C\gt 0$ is the capacitance (in farads), and $E(t)$ is the voltage at time $t.$
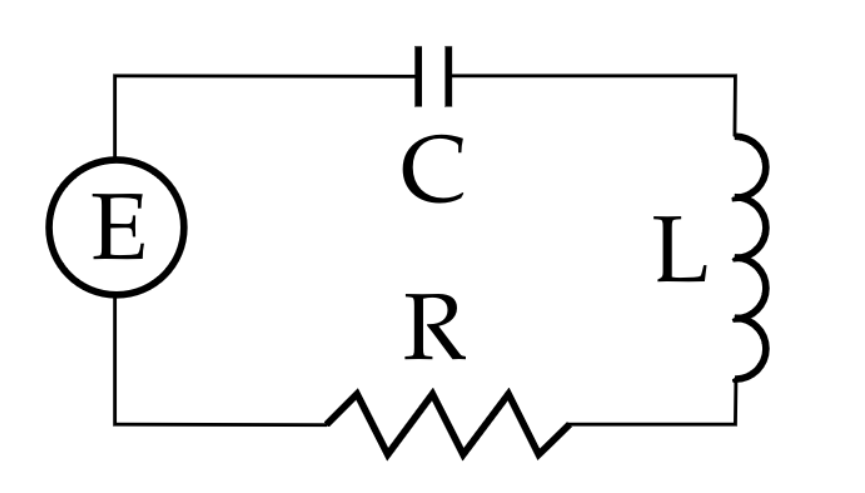
Example
Suppose an RLC series circuit a has a $0.1$-henry inductor, a $0.625$-farad capacitor, and a $0.6$-ohm resistor.
Furthermore, at $t=0,$ the current is $1$ ampere and $I'(0)=0.$
Finally, the circuit is supplied with a constant voltage by a battery.
Find the equation which describes the current $I$ at time $t.$

Since the voltage source is constant, we know that $E'(t)$ is $0$ for all $t.$
So, the current $I$ is governed by the equation $$ 0.1I''+0.6I'+\frac{1}{0.625}I=0 $$ or, more simply after multiplying through by $10,$ $$ I''+6I'+16I=0 $$ with initial conditions $I(0)=1$ and $I'(0)=0.$
The characteristic equation is $$ r^2+6r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-6\pm\sqrt{(6)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{36-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{-28}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2\sqrt{-7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2i\sqrt{7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=-3 \pm i\sqrt{7} &\mbox{}\\ \end{array} $$ So, we have complex conjugate roots $-3 \pm i\sqrt{7}.$
It follows that our general solution is $$ I(t)=C_1e^{-3t}\cos(\sqrt{7}t)+C_2e^{-3t}\sin(\sqrt{7}t) $$ Thus, we also have $$ I'(t)=(-3C_1+C_2\sqrt{7})e^{-3t}\cos(\sqrt{7}t)+(-C_1\sqrt{7}-3C_2)e^{-3t}\sin(\sqrt{7}t) $$ Satisfying the initial conditions, $I(0)=1$ and $I'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -3C_1+C_2\sqrt{7}=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=\frac{3}{\sqrt{7}} $$ The equation giving current as a function of time is $$ I(t)=e^{-3t}\cos(\sqrt{7}t)+\frac{3}{\sqrt{7}}e^{-3t}\sin(\sqrt{7}t) $$ The graph of $I(t)$ is seen below.
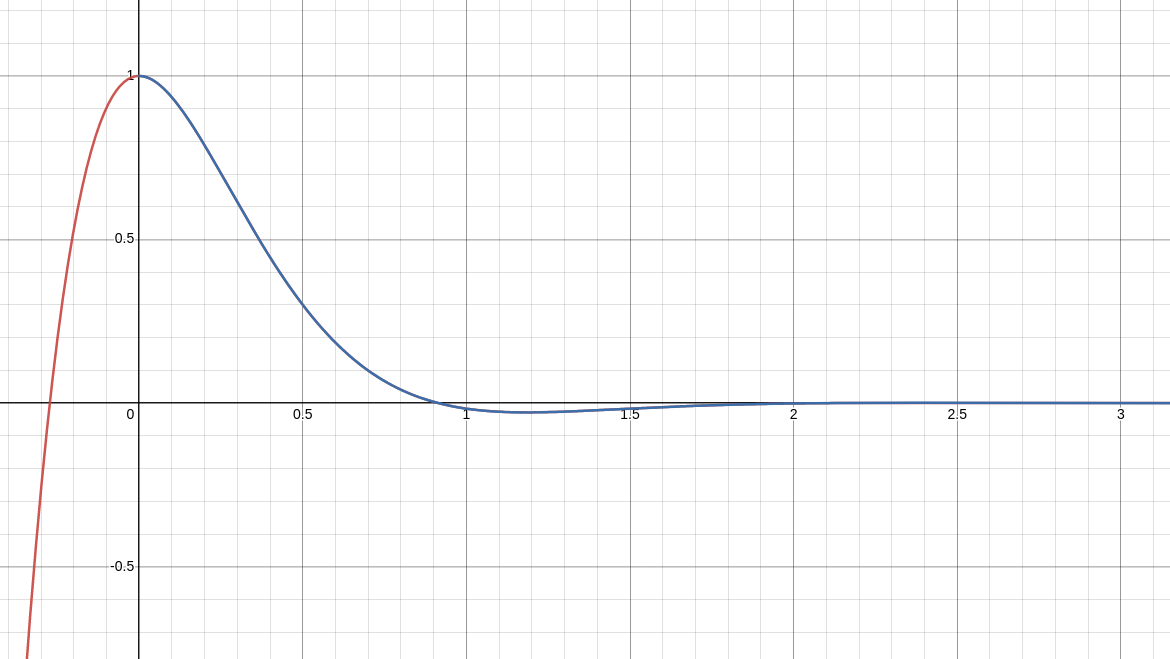
So, the current $I$ is governed by the equation $$ 0.1I''+0.6I'+\frac{1}{0.625}I=0 $$ or, more simply after multiplying through by $10,$ $$ I''+6I'+16I=0 $$ with initial conditions $I(0)=1$ and $I'(0)=0.$
The characteristic equation is $$ r^2+6r+16=0. $$ Then, $$ \begin{array}{lll} \displaystyle r&\displaystyle=\frac{-6\pm\sqrt{(6)^2-4(1)(16)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{36-64}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm\sqrt{-28}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2\sqrt{-7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 2i\sqrt{7}}{2} &\mbox{}\\ \displaystyle &\displaystyle=-3 \pm i\sqrt{7} &\mbox{}\\ \end{array} $$ So, we have complex conjugate roots $-3 \pm i\sqrt{7}.$
It follows that our general solution is $$ I(t)=C_1e^{-3t}\cos(\sqrt{7}t)+C_2e^{-3t}\sin(\sqrt{7}t) $$ Thus, we also have $$ I'(t)=(-3C_1+C_2\sqrt{7})e^{-3t}\cos(\sqrt{7}t)+(-C_1\sqrt{7}-3C_2)e^{-3t}\sin(\sqrt{7}t) $$ Satisfying the initial conditions, $I(0)=1$ and $I'(0)=0,$ we have $$ \begin{cases} C_1=1\\ -3C_1+C_2\sqrt{7}=0\\ \end{cases} $$ Solving this system, $$ C_1=1\,\,\,\,\mbox{and}\,\,\,\,C_2=\frac{3}{\sqrt{7}} $$ The equation giving current as a function of time is $$ I(t)=e^{-3t}\cos(\sqrt{7}t)+\frac{3}{\sqrt{7}}e^{-3t}\sin(\sqrt{7}t) $$ The graph of $I(t)$ is seen below.
