The generalization of the flux form of Green's Theorem is called the Divergence Theorem (or Gauss' Theorem).
We will see that this theorem is also indispensable to describing the physics of electricity and magnetism.
The Divergence Theorem, together with the other results we've discussed in this course, hint at a much larger and beautiful pattern in higher dimensions.
In fact, we will see that all the results of this chapter are really just higher-dimensional analogues of the Fundamental Theorem of Calculus.
The Divergence Theorem
Let $S$ be a piecewise, smooth closed surface that encloses solid $E$ in space. Assume that $S$ is oriented outward (positively), and let ${\bf F} $ be a vector field with continuous partial derivatives on an open region containing $E.$ Then $$\iint_{S} {\bf F}\cdot d{\bf S}=\iiint_{E} \mbox{div } {\bf F} \, dV $$
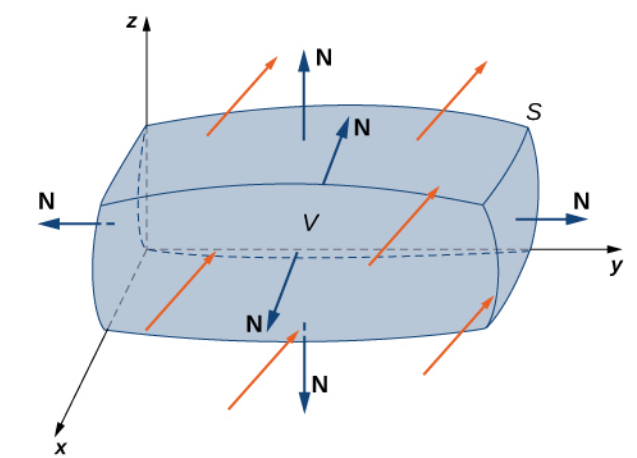
Various Notations of the Divergence Theorem $$ \begin{array}{ll} \displaystyle \iint_{S} {\bf F}\cdot d{\bf S} &= \displaystyle \iint_{S} {\bf F}\cdot {\bf N} \, dS\\ &= \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf F}\cdot {\bf N} \, dS\\ &=\displaystyle \iiint_{E} \mbox{div }{\bf F} \,dV \\ &=\displaystyle \iiint_{E} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) \,dV \\ &=\displaystyle \iiint_{E} \nabla \cdot {\bf F} \, dV \\ \end{array} $$
Example
Verify the divergence theorem for vector field ${\bf F} = \langle x - y, x + z, z - y \rangle$ and surface $S$ that consists of cone $x^2 + y^2 = z^2,$ $0 \leq z \leq 1,$ and the circular top of the cone. Assume this surface is positively oriented (outward).

By a previous calculation, we saw directly that $\displaystyle \iint_S {\bf F}\cdot\, d{\bf S}=\frac{2\pi}{3}.$
We now use the Divergence Theorem to find the flux over the 3D region $E.$ $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}(x - y)+\frac{\partial }{\partial y}(x + z)+\frac{\partial }{\partial z}(z - y ) \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 1+0+1 \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2\iiint_{E} \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2\cdot \frac{\pi}{3} &\mbox{volume of a cone with radius 1 and height 1}\\ \displaystyle &\displaystyle= \frac{2\pi}{3} &\mbox{}\\ \end{array} $$
Example
Verify the divergence theorem for vector field ${\bf F} = x^2{\bf i}+y^2{\bf j}+z^2{k}$ through the surface $C$ which consists of the cylinder $x^2 + y^2 = 1,$ $-1 \leq z \leq 1$ including the top and bottom.
Assume this surface is positively (outwardly) oriented.
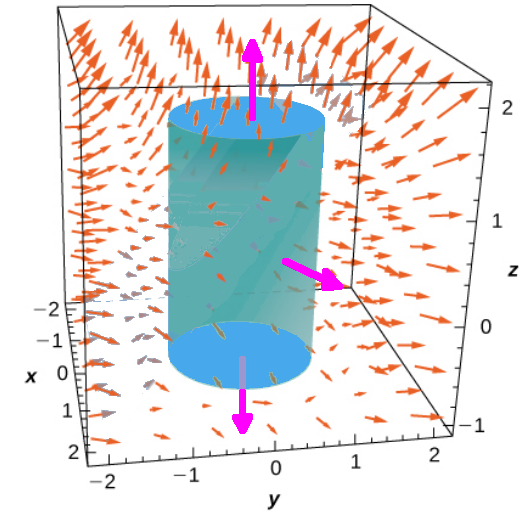
In a previous section we calculated the flux through the cylinder $C$ and its
top $T$ and bottom $B$.
Using these results we have $\displaystyle \iint_S {\bf F}\cdot\, d{\bf S}=\iint_C {\bf F}\cdot\, d{\bf S}+\iint_T {\bf F}\cdot\, d{\bf S}+\iint_B {\bf F}\cdot\, d{\bf S}=0+\pi+(-\pi)=0.$
We now use the Divergence Theorem to find the flux over the 3D region $E.$ $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}x^2+\frac{\partial }{\partial y}y^2+\frac{\partial }{\partial z}z^2 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+2y+2z \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2\iiint_{E} x+y+z \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\int_{0}^{1} (r\cos \theta +r\sin \theta +z)\, r\,dr\,d\theta \, dz&\mbox{convert to cylindrical coordinates}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\int_{0}^{1} r^2\cos \theta +r^2\sin \theta +rz\,dr\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\left[\frac{1}{3}r^3\cos \theta +\frac{1}{3}r^3\sin \theta +\frac{1}{2}r^2z\right]_{0}^{1}\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\frac{1}{3}\cos \theta +\frac{1}{3}\sin \theta +\frac{1}{2}z\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[\frac{1}{3}\sin \theta -\frac{1}{3}\cos \theta +\frac{1}{2}z\theta \right]_{0}^{2\pi} \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[\frac{1}{3}\sin(2\pi) -\frac{1}{3}\cos (2\pi) +\frac{1}{2}z(2\pi)-\left(\frac{1}{3}\sin(0) -\frac{1}{3}\cos(0) +\frac{1}{2}\cdot 0\right) \right] \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[-\frac{1}{3} +\pi z-\left( -\frac{1}{3}\right) \right] \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\pi z \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \int_{-1}^{1} z \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \left[\frac{1}{2}z^2\right]_{-1}^{1}&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \cdot 0&\mbox{}\\ \displaystyle &\displaystyle= 0 & \mbox{}\\ \end{array} $$
Using these results we have $\displaystyle \iint_S {\bf F}\cdot\, d{\bf S}=\iint_C {\bf F}\cdot\, d{\bf S}+\iint_T {\bf F}\cdot\, d{\bf S}+\iint_B {\bf F}\cdot\, d{\bf S}=0+\pi+(-\pi)=0.$
We now use the Divergence Theorem to find the flux over the 3D region $E.$ $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}x^2+\frac{\partial }{\partial y}y^2+\frac{\partial }{\partial z}z^2 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+2y+2z \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2\iiint_{E} x+y+z \, dV&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\int_{0}^{1} (r\cos \theta +r\sin \theta +z)\, r\,dr\,d\theta \, dz&\mbox{convert to cylindrical coordinates}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\int_{0}^{1} r^2\cos \theta +r^2\sin \theta +rz\,dr\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\left[\frac{1}{3}r^3\cos \theta +\frac{1}{3}r^3\sin \theta +\frac{1}{2}r^2z\right]_{0}^{1}\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\int_{0}^{2\pi}\frac{1}{3}\cos \theta +\frac{1}{3}\sin \theta +\frac{1}{2}z\,d\theta \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[\frac{1}{3}\sin \theta -\frac{1}{3}\cos \theta +\frac{1}{2}z\theta \right]_{0}^{2\pi} \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[\frac{1}{3}\sin(2\pi) -\frac{1}{3}\cos (2\pi) +\frac{1}{2}z(2\pi)-\left(\frac{1}{3}\sin(0) -\frac{1}{3}\cos(0) +\frac{1}{2}\cdot 0\right) \right] \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\left[-\frac{1}{3} +\pi z-\left( -\frac{1}{3}\right) \right] \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2 \int_{-1}^{1}\pi z \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \int_{-1}^{1} z \, dz&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \left[\frac{1}{2}z^2\right]_{-1}^{1}&\mbox{}\\ \displaystyle &\displaystyle= 2\pi \cdot 0&\mbox{}\\ \displaystyle &\displaystyle= 0 & \mbox{}\\ \end{array} $$
Scenic Vista: The Divergence Theorem is a generalization of the flux (normal) form of Green's Theorem. $$ \begin{array}{ll} \displaystyle \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf F}\cdot d{\bf S}=\displaystyle \iiint_{E} \mbox{div }{\bf F} \,dV=\displaystyle \iiint_{E} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) \,dV& \mbox{Divergence Theorem} \end{array} $$

Advantages of the Divergence Theorem
As with Stokes' Theorem, one of the great advantages of the Divergence Theorem is that it gives us options.
For example, calculating a messy surface integral $\displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf F}\cdot d{\bf S}$ could be greatly simplified by calculating the triple integral $\displaystyle \iiint_{E} \mbox{div }{\bf F} \,dV$ instead.
Example
Use the divergence theorem to calculate flux integral $\displaystyle \iint_{S} {\bf F}\cdot d{\bf S}$ where $S$ is the boundary of the box given by $0 \leq x \leq 2,$ $1 \leq y \leq 4,$ $0 \leq z \leq 1,$ and ${\bf F} = \langle x^2 + yz, y - z, 2x + 2y + 2z \rangle.$
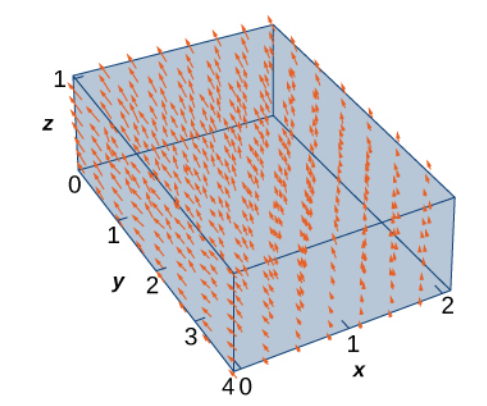
We could parameterize all six surfaces over their respective regions, requiring six separate integrals. Or...
We could use divergence theorem!
$$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}( x^2 + yz)+\frac{\partial }{\partial y}(y - z)+\frac{\partial }{\partial z}(2x + 2y + 2z ) \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+1+2 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+3 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\int_{1}^{4}\int_{0}^{1} 2x+3 \, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}(2x+3)\left(\int_{1}^{4}\int_{0}^{1} \, dz \, dy\right) \, dx&\mbox{}\\ \displaystyle &\displaystyle= \left(\int_{0}^{2}(2x+3) \, dx \right)\left(\int_{1}^{4}\int_{0}^{1} \, dz \, dy\right)&\mbox{}\\ \displaystyle &\displaystyle= \left[(x^2+3x)\right]_{0}^{2}(4-1)(1-0)&\mbox{}\\ \displaystyle &\displaystyle= \left((2^2+3(2)\right)(3)(1)&\mbox{}\\ \displaystyle &\displaystyle= 10\cdot 3&\mbox{}\\ \displaystyle &\displaystyle= 30&\mbox{}\\ \end{array} $$
We could use divergence theorem!
$$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}( x^2 + yz)+\frac{\partial }{\partial y}(y - z)+\frac{\partial }{\partial z}(2x + 2y + 2z ) \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+1+2 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \iiint_{E} 2x+3 \, dV&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}\int_{1}^{4}\int_{0}^{1} 2x+3 \, dz \, dy \, dx&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2}(2x+3)\left(\int_{1}^{4}\int_{0}^{1} \, dz \, dy\right) \, dx&\mbox{}\\ \displaystyle &\displaystyle= \left(\int_{0}^{2}(2x+3) \, dx \right)\left(\int_{1}^{4}\int_{0}^{1} \, dz \, dy\right)&\mbox{}\\ \displaystyle &\displaystyle= \left[(x^2+3x)\right]_{0}^{2}(4-1)(1-0)&\mbox{}\\ \displaystyle &\displaystyle= \left((2^2+3(2)\right)(3)(1)&\mbox{}\\ \displaystyle &\displaystyle= 10\cdot 3&\mbox{}\\ \displaystyle &\displaystyle= 30&\mbox{}\\ \end{array} $$
Fluid Dynamics
Suppose that a vector field ${\bf v}$ represents the velocity of a flowing fluid.
Then the flux $\displaystyle \iint_{S} {\bf v}\cdot d{\bf S}$ represents the amount of fluid flowing through a surface $S$ per unit time.
If $S$ is a closed surface, such as the cube below, and the fluid is incompressible (such as water), what can we say about the flux through $S?$ $(\mbox{rate fluid leaves}-\mbox{rate fluid enters})$

Generally Speaking...
Let ${\bf v}$ be a velocity field for a fluid.
The fluid is incompressible if $$\mbox{div }{\bf v}=\nabla \cdot {\bf v}=0.$$
Big Question: What does the Divergence Theorem have to say about incompressible fluid flows?
If $\mbox{div }{\bf v}=\nabla \cdot {\bf v}=0$ (the fluid is incompressible), then, by the Divergence Theorem,
the net flux $(\mbox{rate fluid leaves}-\mbox{rate fluid enters})$ through a closed surface
$S$ will always be
$$
\iint_S {\bf v}\cdot\, d{\bf S}=\iiint_{E} \mbox{div }{\bf v} \, dV=\iiint_{E} 0 \, dV=0
$$
This makes, sense right?
Example
Let $\displaystyle {\bf v}=\left \langle-\frac{y}{z},\frac{x}{z},0\right \rangle$ be the velocity field of a fluid. Let $C$ be the solid cube given by $1 \leq x \leq 4,$ $2 \leq y \leq 5,$ $1 \leq z \leq 4,$ and let $S$ be the boundary of this cube. Find the flow rate of the fluid across $S.$

Using the Divergence Theorem,
$$
\begin{array}{lll}
\displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iiint_{E} \mbox{div }{\bf F} \, dV &\mbox{}\\
\displaystyle &\displaystyle=\iiint_{E} \nabla \cdot {\bf F} \, dV &\mbox{}\\
\displaystyle &\displaystyle= \iiint_{E} \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \, dV&\mbox{}\\
\displaystyle &\displaystyle= \iiint_{E} \frac{\partial }{\partial x}(-\frac{y}{z})+\frac{\partial }{\partial y}(\frac{x}{z})+\frac{\partial }{\partial z}(0) \, dV&\mbox{}\\
\displaystyle &\displaystyle= \iiint_{E} 0+0+0 \, dV&\mbox{}\\
\displaystyle &\displaystyle= \iiint_{E} 0 \, dV&\mbox{}\\
\displaystyle &\displaystyle= 0&\mbox{}\\
\end{array}
$$
Is it any surprise?
Fun Fact
If ${\bf F}=\left \langle P(z,y),Q(x,z),R(x,y)\right \rangle,$ then $\mbox{div }{\bf F}=0.$
The Divergence Theorems then says that the flux of ${\bf F}$ though any closed surface $S$ over which ${\bf F}$ is well behaved, will be zero. $$ \iint_{S} {\bf F}\cdot d{\bf S} = \iiint_{E} \mbox{div }{\bf F} \,dV = \iiint_{E} 0 \,dV=0\\ $$
Example
Find $$\displaystyle \iint_{S} {\bf F}\cdot d{\bf S}$$ if ${\bf F} = \langle \sin(y)e^{yz}, x^2 z^2, \cos(xy)e^{\sin x}\rangle.$
Clearly $\mbox{div }{\bf F}=0.$
It follows that $\displaystyle \iint_{S} {\bf F}\cdot d{\bf S}=0.$
It follows that $\displaystyle \iint_{S} {\bf F}\cdot d{\bf S}=0.$
Electrostatic Fields. Suppose that $Q$ is a stationary point charge located at the origin. Then the electric field in three dimensions is $$ {\bf E}(x,y,z) = \left \langle \frac{Q}{4\pi\varepsilon_0}\frac{x}{(x^2+y^2+z^2)^{3/2}},\frac{Q}{4\pi\varepsilon_0}\frac{y}{(x^2+y^2+z^2)^{3/2}},\frac{Q}{4\pi\varepsilon_0}\frac{z}{(x^2+y^2+z^2)^{3/2}}\right\rangle $$
(a) Show that $\mbox{div }{\bf E}=0$ when $(x,y,z)\neq(0,0,0).$
(b) Calculate the electric flux of ${\bf E},$ that is $\displaystyle \iint_{S} {\bf E}\cdot d{\bf S}$, through a closed surface $S$ not containing the origin.
(a) If $(x,y,z)\neq(0,0,0),$ then
$$
\begin{array}{lll}
\displaystyle \mbox{div }{\bf E}&\displaystyle=\nabla \cdot {\bf E} &\mbox{}\\
\displaystyle &\displaystyle= \frac{\partial}{\partial x}\left(\frac{Q}{4\pi\varepsilon_0}\frac{x}{(x^2+y^2+z^2)^{3/2}}\right)+\frac{\partial}{\partial y}\left(\frac{Q}{4\pi\varepsilon_0}\frac{y}{(x^2+y^2+z^2)^{3/2}}\right)+\frac{\partial}{\partial z}\left(\frac{Q}{4\pi\varepsilon_0}\frac{z}{(x^2+y^2+z^2)^{3/2}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{\partial}{\partial x}\frac{x}{(x^2+y^2+z^2)^{3/2}}+\frac{\partial}{\partial y}\frac{y}{(x^2+y^2+z^2)^{3/2}}+\frac{\partial}{\partial z}\frac{z}{(x^2+y^2+z^2)^{3/2}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{(x^2+y^2+z^2)^{3/2}\cdot 1-x\cdot \left(\frac{3}{2}(x^2+y^2+z^2)^{1/2}\cdot 2x\right)}{(x^2+y^2+z^2)^{3}}+\frac{(x^2+y^2+z^2)^{3/2}\cdot 1-y\cdot \left(\frac{3}{2}(x^2+y^2+z^2)^{1/2}\cdot 2y\right)}{(x^2+y^2+z^2)^{3}}+\frac{(x^2+y^2+z^2)^{3/2}\cdot 1-z\cdot \left(\frac{3}{2}(x^2+y^2+z^2)^{1/2}\cdot 2z\right)}{(x^2+y^2+z^2)^{3}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{(x^2+y^2+z^2)^{3/2}-3x^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}+\frac{(x^2+y^2+z^2)^{3/2}-3y^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}+\frac{(x^2+y^2+z^2)^{3/2}-3z^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{(x^2+y^2+z^2)^{3/2}-3x^2(x^2+y^2+z^2)^{1/2}+(x^2+y^2+z^2)^{3/2}-3y^2(x^2+y^2+z^2)^{1/2}+(x^2+y^2+z^2)^{3/2}-3z^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{3(x^2+y^2+z^2)^{3/2}-3(x^2+y^2+z^2)(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^{3}}\right)&\mbox{}\\
\displaystyle &\displaystyle= \frac{Q}{4\pi\varepsilon_0}\left(\frac{3(x^2+y^2+z^2)^{3/2}-3(x^2+y^2+z^2)^{3/2}}{(x^2+y^2+z^2)^{3}}\right)&\mbox{}\\
\displaystyle &\displaystyle= 0&\mbox{}\\
\end{array}
$$
(b) Since $\mbox{div }{\bf F}=0,$ the Divergence Theorem tells us
$$
\mbox{Electric Flux}=\iint_{S} {\bf E}\cdot d{\bf S}=\iiint_{E} \mbox{div }{\bf E} \, dV=\iiint_{E} 0 \, dV=0.
$$
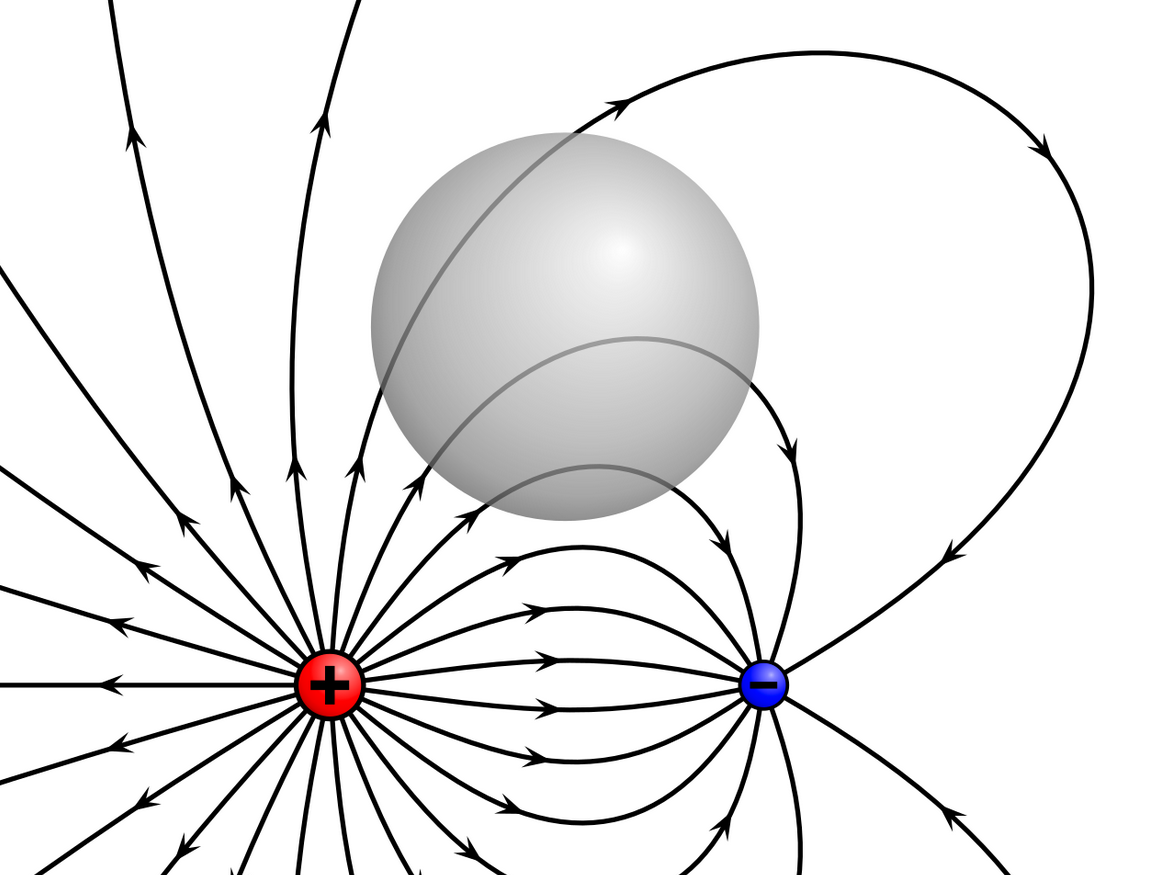
Electric Kitty Has a Question for You!
What happens if the closed surface $S$ contains the origin?

Electric Kitty Has an Answer (and More Questions) for You!
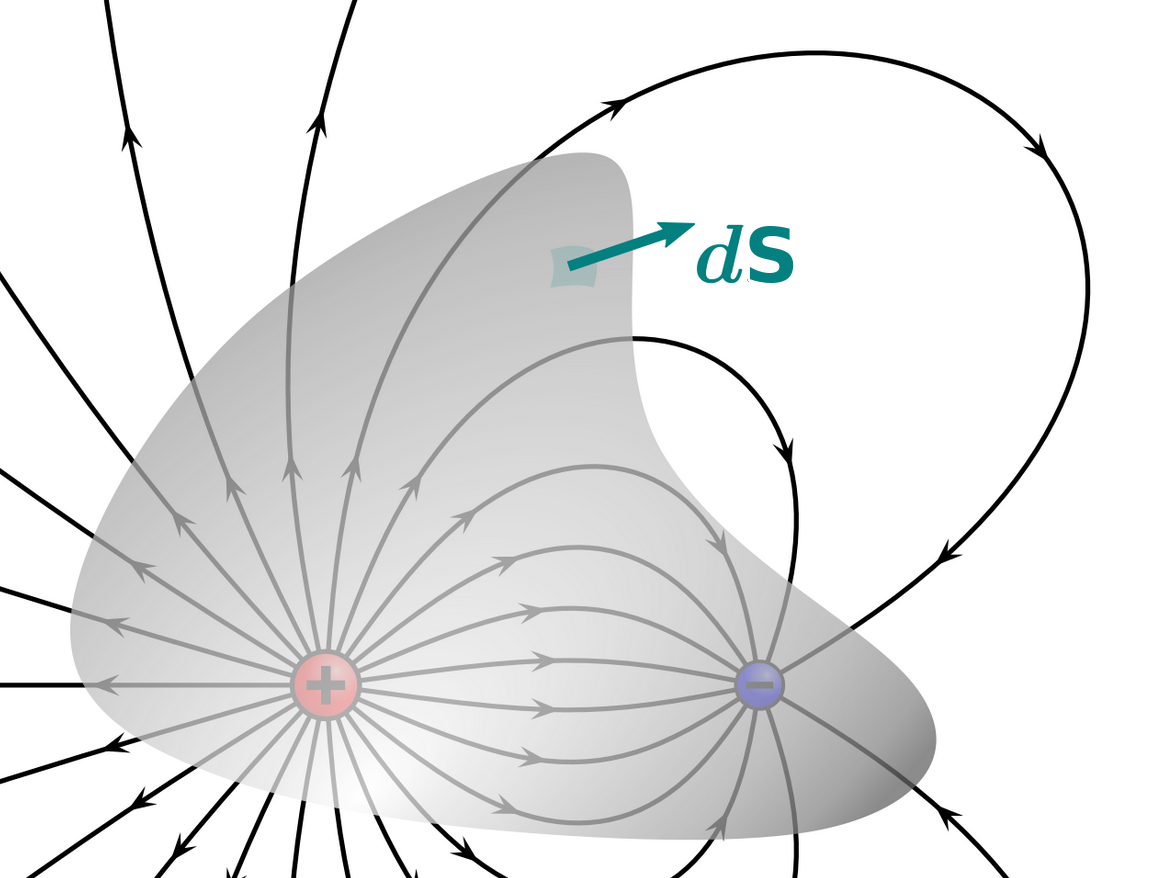
If the closed surface $S$ contains the origin, then $$ \displaystyle \iint_{S} {\bf E}\cdot d{\bf S}=\frac{Q}{\varepsilon_0} $$ This is not an easy calculation because the Divergence Theorem doesn't apply directly. (Why is this the case??????)
We need to do some shenanigans in order to apply the Divergence Theorem.
The above results make up the basis for one of the great laws of electromagnetism: Gauss' Law.
Gauss' Law
Suppose that $Q$ is a stationary point charge and $S$ is a closed, piecewise-smooth surface. Then $$ \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}=\begin{cases}0 & \mbox{if $S$ does not contain $Q$} \\ \displaystyle \frac{Q}{\varepsilon_0} & \mbox{if $S$ contains $Q$}\end{cases} $$
Gauss' Law (Alternative Statement)
Suppose that $Q$ is the net charge within a closed, piecewise-smooth surface $S,$ then $$ \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}=\frac{Q}{\varepsilon_0} $$


Example
Suppose we have four stationary point charges in space, all with a charge of $0.002$ Coulombs (C). The charges are located at $(0, 1, 1),$ $(1, 1, 4),$ $(-1, 0, 0),$ and $(-2, -2, 2).$
Let ${\bf E}$ denote the electrostatic field generated by these point charges.
If $S$ is the sphere of radius $2$ oriented outward (positively) and centered at the origin, then find $\displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}.$
Note: $\varepsilon_0 \approx 8.854 \times 10^{-12}$ farads per meter.
The distances of each point from the origin are
$$
\begin{array}{lll}
\displaystyle (0, 1, 1):&\displaystyle d=\sqrt{0^2+1^1+1^2}=\sqrt{2}\lt 2 &\mbox{ inside sphere}\\
\displaystyle (1, 1, 4):&\displaystyle d=\sqrt{1^2+1^2+4^2}=\sqrt{18}\gt 2 &\mbox{outside sphere}\\
\displaystyle (-1, 0, 0):&\displaystyle d=\sqrt{(-1)^1+0^2+0^2+0^2}=\sqrt{1}=1\lt 2 &\mbox{inside sphere}\\
\displaystyle (-2, -2, -2):&\displaystyle d=\sqrt{(-2)^2+(-2)^2+(-2)^2}=\sqrt{12}\gt 2 &\mbox{outside sphere}\\
\end{array}
$$
Thus, there is a total charge of $Q=2\cdot 0.002=0.004$ coulombs within the sphere.
By Gauss' Law we have $$ \begin{array}{ll} \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}&= \displaystyle \frac{Q}{\varepsilon_0}\\ \displaystyle &\approx \displaystyle \frac{0.004}{8.854 \times 10^{-12}}\\ \displaystyle &=451773209.8\\ \displaystyle &=4.517732098\times 10^8\\ \end{array} $$ where the above is in $\mbox{V-m}$
By Gauss' Law we have $$ \begin{array}{ll} \displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}&= \displaystyle \frac{Q}{\varepsilon_0}\\ \displaystyle &\approx \displaystyle \frac{0.004}{8.854 \times 10^{-12}}\\ \displaystyle &=451773209.8\\ \displaystyle &=4.517732098\times 10^8\\ \end{array} $$ where the above is in $\mbox{V-m}$
Electric Kitty Has an Awesome Idea!
We stated Gauss' Law above in integral form.
Let's use the Divergence Theorem to rewrite Gauss' Law in differential form!

Suppose that $Q$ is the net charge within a closed, piecewise-smooth surface $S,$ then Gauss' Law is
$$
\displaystyle {\large \subset\!\!\supset}\kern-1.7em \iint_{S} {\bf E}\cdot d{\bf S}=\frac{Q}{\varepsilon_0}
$$
The Divergence Theorem then gives us
$$
\displaystyle \iiint_{E} \nabla \cdot {\bf E}\,dV=\frac{Q}{\varepsilon_0}
$$
Now if $\rho$ is the charge density within the region $E,$ then the the total amount of charge $Q$ in $E$ is
$
\displaystyle \iiint_{E} \rho \, dV.
$
Then it follows that $$ \displaystyle \iiint_{E} \nabla \cdot {\bf E}\,dV=\frac{1}{\varepsilon_0}\iiint_{E} \rho \,dV=\iiint_{E} \frac{\rho}{\varepsilon_0} \,dV $$ Since the above statement holds for every possible piecewise-smooth surface $S$, it can be shown that $$ \displaystyle \nabla \cdot {\bf E}= \frac{\rho}{\varepsilon_0} $$ which is the differential form of Gauss' Law.
We also note that this is one of Maxwell's equations!
Then it follows that $$ \displaystyle \iiint_{E} \nabla \cdot {\bf E}\,dV=\frac{1}{\varepsilon_0}\iiint_{E} \rho \,dV=\iiint_{E} \frac{\rho}{\varepsilon_0} \,dV $$ Since the above statement holds for every possible piecewise-smooth surface $S$, it can be shown that $$ \displaystyle \nabla \cdot {\bf E}= \frac{\rho}{\varepsilon_0} $$ which is the differential form of Gauss' Law.
We also note that this is one of Maxwell's equations!
Scenic Vista: The Divergence Theorem is a generalization of the flux form of Green's Theorem and the FTC. $$ \begin{array}{ll} \displaystyle \iiint_{E} \nabla \cdot {\bf F} \, dV = \iiint_{E} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) \,dV = {\large \subset\!\!\supset}\kern-1.7em \iint_{S=\partial E} {\bf F}\cdot {\bf N} \, dS& \mbox{Divergence Theorem}\\ \displaystyle \iint_{D} \nabla \cdot {\bf F} \, dA= \iint_{D} \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\right) \,dA = \oint_{C=\partial D} {\bf F}\cdot {\bf N} \, ds& \mbox{Green's Theorem}\\ \displaystyle \int_{I} \nabla \cdot {\bf F} \, dx=\int_{I} \frac{df}{dx}\,dx= f(b)-f(a)={\bf F}(b)\cdot {\bf N}(b)+{\bf F}(a) \cdot {\bf N}(a) & \mbox{FTC}\\ \end{array} $$ The above say that: The sum of the flux densities over the interior of a region is equal to the total flux (total change) at the boundary.
Scenic Vista: Stokes' Theorem is a generalization of the circulation form of Green's Theorem. $$ \begin{array}{ll} \displaystyle \iint_{S} \nabla \times {\bf F} \cdot {\bf N} \, dS = \iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \,dS = \oint_{C=\partial S} {\bf F}\cdot {\bf T} \, ds& \mbox{Stokes' Theorem}\\ \displaystyle \iint_{D} \nabla \times {\bf F} \cdot {\bf k}\, dA= \iint_{D} \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \,dA = \oint_{C=\partial D} {\bf F}\cdot {\bf T} \, ds& \mbox{Green's Theorem}\\ \end{array} $$ The above say that: The sum of the circulation densities over the interior of a region is equal to the total circulation (total change) at the boundary.
Scenic Vista: The FTLI is also a generalization of the FTC. $$ \begin{array}{ll} \displaystyle \int_{(x_1,y_1,z_1)}^{(x_2,y_2,z_2)} \nabla f \cdot {\bf T} \, ds=\int_{(x_1,y_1,z_1)}^{(x_2,y_2,z_2)} \left(\frac{\partial f}{\partial x}\,dx+\frac{\partial f}{\partial y}\,dy+\frac{\partial f}{\partial z}\,dz\right) = f(x_2,y_2,z_2)-f(x_1,y_1,z_1)& \mbox{}\\ \displaystyle \int_{(x_1,y_1)}^{(x_2,y_2)} \nabla f \cdot {\bf T} \, ds=\int_{(x_1,y_1)}^{(x_2,y_2)} \left(\frac{\partial f}{\partial x}\,dx+\frac{\partial f}{\partial y}\,dy\right) = f(x_2,y_2)-f(x_1,y_1)& \mbox{}\\ \displaystyle \int_{x_1}^{x_2} \nabla f \cdot {\bf i} \, dx=\int_{x_1}^{x_2} \frac{df}{dx}\,dx= f(x_2)-f(x_1) & \mbox{}\\ \end{array} $$ The above say that: The sum of the tangential components of the gradient vector the over the interior of a curve (a one-dimensional region) is equal to the total change at the boundary.
Scenic Vista: The Big Picture
| FTC | $\displaystyle \int_{[a,b]} \nabla \cdot {\bf F} \, dx={\bf F}(b)\cdot {\bf N}(b)+{\bf F}(a) \cdot {\bf N}(a)$ |  |
| FTLI | $\displaystyle\int_C \nabla f \cdot d{\bf r}=f({\bf r}(b))-f({\bf r}(a))$ | 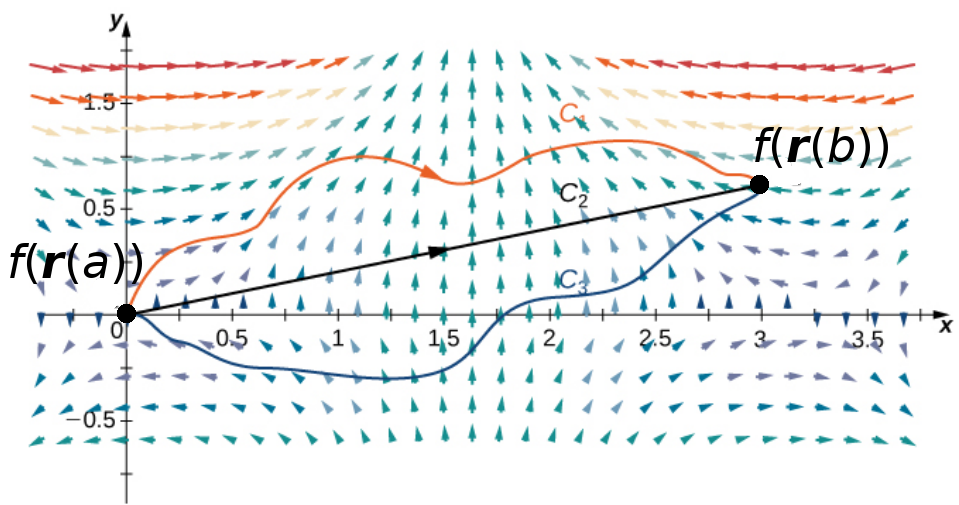 |
| Green's Theorem (Circulation Form) | $\displaystyle \iint_{D} \nabla \times {\bf F} \cdot {\bf k}\, dA = \oint_{C=\partial D} {\bf F}\cdot {\bf T} \, ds$ |  |
| Green's Theorem (Flux Form) | $\displaystyle \iint_{D} \nabla \cdot {\bf F} \, dA = \oint_{C=\partial D} {\bf F}\cdot {\bf N} \, ds$ | 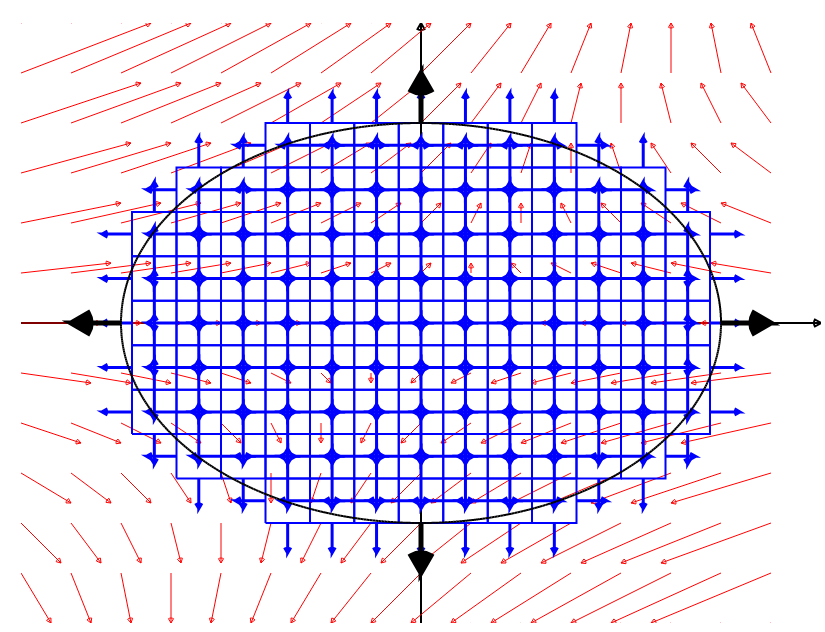 |
| Stokes' Theorem | $\displaystyle \iint_{S} \nabla \times {\bf F} \cdot {\bf N} \, dS = \iint_{S} \mbox{curl }{\bf F} \cdot {\bf N} \,dS = \oint_{C=\partial S} {\bf F}\cdot {\bf T} \, ds$ |  |
| Divergence Theorem | $\displaystyle \iiint_{E} \nabla \cdot {\bf F} \, dV = {\large \subset\!\!\supset}\kern-1.7em \iint_{S=\partial E} {\bf F}\cdot {\bf N} \, dS$ | 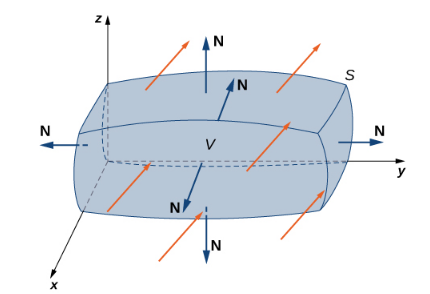 |
The sum (integral) of a differential operator of $\Phi$ over the interior of a region $R$ is equal to the total change of $\Phi$ at the boundary $\partial R.$
Scenic Vista: The Big Picture
The sum (integral) of a differential operator of $\Phi$ over the interior of a region $R$ is equal to the total change of $\Phi$ at the boundary $\partial R.$ $$\int_{R} \,d\Phi=\int_{\partial R} \Phi$$
Scenic Vista: Maxwell's Equations
| Integral Form | Differential Form | |
| Gauss' Law | $${\large \subset\!\!\supset}\kern-1.7em \iint_{\partial R} {\bf E}\cdot d{\bf S}=\frac{1}{\varepsilon_0}\iiint_{R} \rho \, dV =\frac{Q}{\varepsilon_0}$$ | $$\nabla \cdot {\bf E}=\frac{\rho}{\varepsilon_0}$$ |
| Gauss' Magnetism Law | $${\large \subset\!\!\supset}\kern-1.7em \iint_{\partial R} {\bf B}\cdot d{\bf S}=0$$ | $$\nabla \cdot {\bf B}=0$$ |
| Faraday's Law of Induction | $$\oint_{\partial S} {\bf E} \cdot d{\bf r}=-\frac{d}{dt}\iint_{S} {\bf B} \cdot d{\bf S} $$ | $$\nabla \times {\bf E}=-\frac{\partial {\bf B}}{\partial t}$$ |
| Ampère's Law | $$\oint_{\partial S} {\bf B} \cdot d{\bf r}=\mu_0\left( \iint_{S}{\bf J}\cdot d{\bf S} + \varepsilon_0 \frac{d}{dt}\iint_{S} {\bf E} \cdot d{\bf S} \right)$$ | $$\nabla \times {\bf B}=\mu_0 \left({\bf J}+\varepsilon_0 \frac{\partial {\bf E}}{\partial t}\right)$$ |
Scenic Vista: Maxwell's Equations in a Vacuum (No Charges $\rho=0$, No Currents, ${\bf J}=0$)
| Electric Field | $$\nabla \cdot {\bf E}=0$$ | $$\nabla \times {\bf E}=-\frac{\partial {\bf B}}{\partial t}$$ |
| Magnetic Field | $$\nabla \cdot {\bf B}=0$$ | $$\nabla \times {\bf B}=\mu_0 \varepsilon_0 \frac{\partial {\bf E}}{\partial t}$$ |
Scenic Vista: Maxwell's Equations in a Vacuum $$ \begin{array}{llll} &\displaystyle \nabla \times {\bf E}&=\displaystyle -\frac{\partial {\bf B}}{\partial t}&\mbox{Faraday's Law in a vacuum}\\ \implies &\displaystyle \nabla \times \nabla \times {\bf E}&=\displaystyle -\frac{\partial}{\partial t}\nabla \times {\bf B}&\mbox{applying curl operator to both sides}\\ \implies&\displaystyle \nabla \times \nabla \times {\bf E}&=\displaystyle -\frac{\partial}{\partial t}\left(\mu_0 \varepsilon_0 \frac{\partial {\bf E}}{\partial t}\right)&\mbox{since $\nabla \times {\bf B}=\mu_0 \varepsilon_0 \frac{\partial {\bf E}}{\partial t}$}\\ \implies&\displaystyle \nabla \times \nabla \times {\bf E}&=\displaystyle -\left(\mu_0 \varepsilon_0 \frac{\partial^2 {\bf E}}{\partial t^2}\right)&\mbox{simplifying}\\ \implies&\displaystyle \nabla (\nabla \cdot {\bf E})-\nabla^2 {\bf E}&=\displaystyle -\left(\mu_0 \varepsilon_0 \frac{\partial^2 {\bf E}}{\partial t^2}\right)&\mbox{using the identity $\nabla \times (\nabla \times {\bf F})=\nabla (\nabla \cdot {\bf F})-\nabla^2 {\bf F}$}\\ \implies&\displaystyle -\nabla^2 {\bf E}&=\displaystyle -\left(\mu_0 \varepsilon_0 \frac{\partial^2 {\bf E}}{\partial t^2}\right)&\mbox{since $\nabla \cdot {\bf E}=0$}\\ \end{array} $$ Thus, $$\frac{\partial^2 {\bf E}}{\partial t^2}=\frac{1}{\mu_0 \varepsilon_0}\nabla^2 {\bf E}=c^2 \nabla^2 {\bf E}$$
Scenic Vista: Maxwell's Equations in a Vacuum
By an argument similar to the above, a similar equation holds for the magnetic field: $$\frac{\partial^2 {\bf B}}{\partial t^2}=\frac{1}{\mu_0 \varepsilon_0}\nabla^2 {\bf B}=c^2 \nabla^2 {\bf B}$$
Scenic Vista: Maxwell's Equations in a Vacuum $$\frac{\partial^2 {\bf E}}{\partial t^2}=\frac{1}{\mu_0 \varepsilon_0}\nabla^2 {\bf E}=c^2 \nabla^2 {\bf E}$$ $$\frac{\partial^2 {\bf B}}{\partial t^2}=\frac{1}{\mu_0 \varepsilon_0}\nabla^2 {\bf B}=c^2 \nabla^2 {\bf B}$$ These two partial differential equations describe wave propagation. They tell us that electric and magnetic fields propagate in empty space at the speed $c=\frac{1}{\sqrt{\mu_0 \varepsilon_0}},$ that is, the speed of light.

Story Time: James Clerk Maxwell

"The agreement of the results seems to show that light and magnetism are affections of the same substance, and that light is an electromagnetic disturbance propagated through the field according to electromagnetic laws".
