Surface integrals are the two-dimensional analog to line integrals.
Evaluating line integrals can be reduced to finding a parameterization of a curve which requires a single parameter $t.$
Today we generalize this process by integrating over surfaces which can be described in terms of two parameters $s$ and $t.$
With line integrals we integrated both scalar functions and vectors fields along curves.
Here we shall do the same, except now it's over surfaces.
Act I
A Crash Course in Parametric Surfaces
A Crash Course in Parametric Surfaces
Recall: Parameterized Curves
Recall that curves in either $\mathbb{R}^2$ or $\mathbb{R}^3$ is parameterized by a single parameter $t.$
A curve $C$ in $\mathbb{R}^3$ is defined parametrically by a single-variable, vector-valued ${\bf r}$ of the form $$ {\bf r}(t)=\langle x(t),y(t),z(t)\rangle $$
Parameterized Surfaces
Surfaces are parameterized by two parameters $s$ and $t.$ A surface $S$ is defined parametrically by a multivariate, vector-valued ${\bf r}$ of the form $$ {\bf r}(s,t)=\langle x(s,t),y(s,t),z(s,t)\rangle $$ ${\bf r}$ maps points $(s,t)$ in the $st$-plane to points $(x,y,z)$ in $3$-dimensional space.
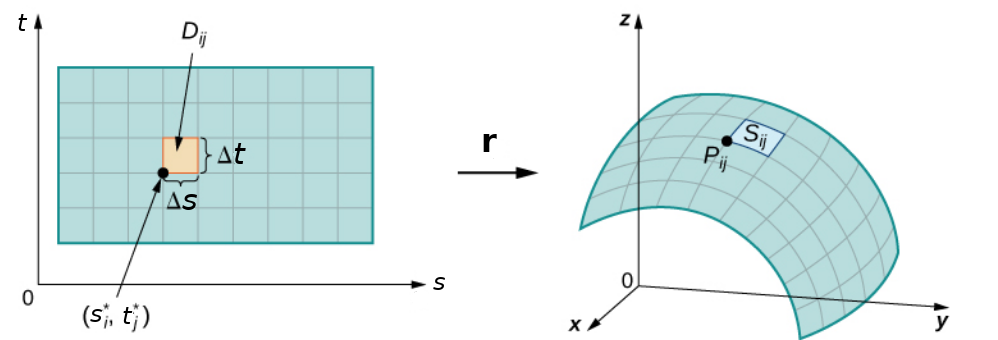
The parameter domain of the parameterization is the set of points in the $st$-plane that can be substituted into ${\bf r}.$
Example
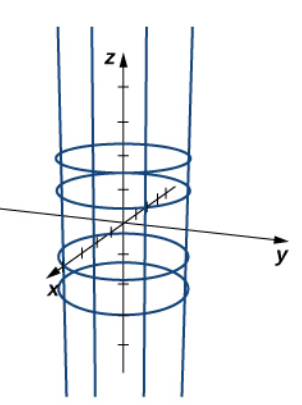
Describe the surface parameterized by $$ {\bf r}(s,t)=\langle \cos s,\sin s, t\rangle $$
Holding one parameter constant get curves in space.
For example, if we let $s$ vary, but hold $t$ constant at the values $t=-2,$ $-1,$ $1,$ and $2,$, we get the following figure.

One the other hand, if we let $t$ but hold $s$ constant at say $s=0,$ $\displaystyle \frac{\pi}{2},$ $\pi,$ and $\displaystyle \frac{3\pi}{2},$ we get the following figure.
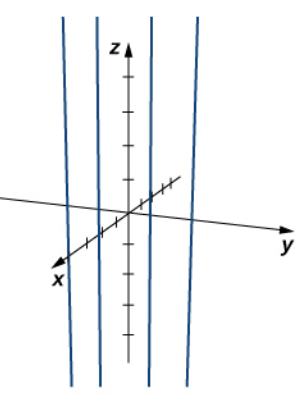
Putting these two together we get
 That is,
$
{\bf r}(s,t)=\langle \cos s,\sin s, t\rangle
$
is the parameterization of a cylinder.
That is,
$
{\bf r}(s,t)=\langle \cos s,\sin s, t\rangle
$
is the parameterization of a cylinder.

For example, if we let $s$ vary, but hold $t$ constant at the values $t=-2,$ $-1,$ $1,$ and $2,$, we get the following figure.

One the other hand, if we let $t$ but hold $s$ constant at say $s=0,$ $\displaystyle \frac{\pi}{2},$ $\pi,$ and $\displaystyle \frac{3\pi}{2},$ we get the following figure.

Putting these two together we get


Example
Describe the surface parameterized by $$ {\bf r}(s, t) = \langle s \cos t, s \sin t, s^2 \rangle,\,\, 0 \leq s \lt \infty,\, 0 \leq t \lt 2\pi. $$
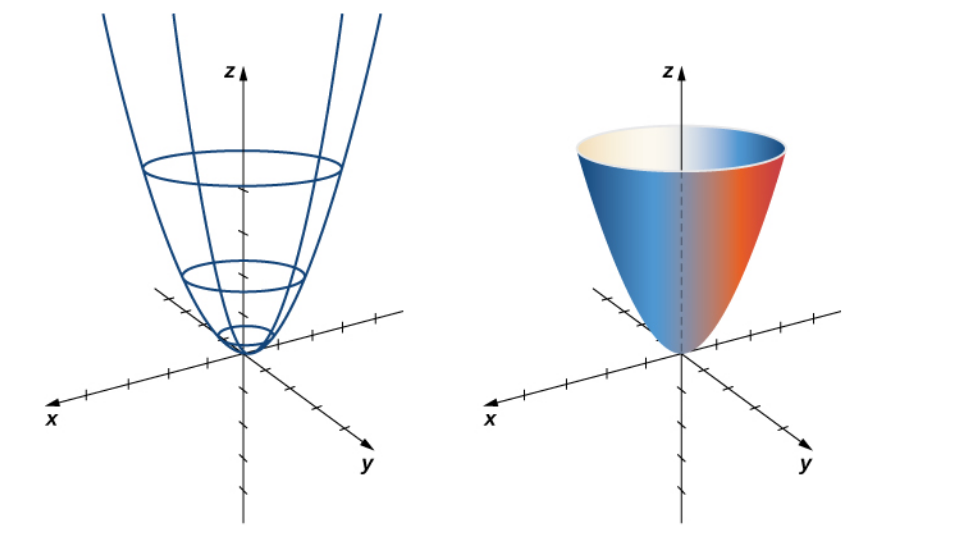
Example
The sphere of radius $\rho$ has parameterization $$ {\bf r}(\phi, \theta) = \langle \rho \cos \theta \sin \phi, \rho \sin \theta \sin \phi, \rho \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. $$
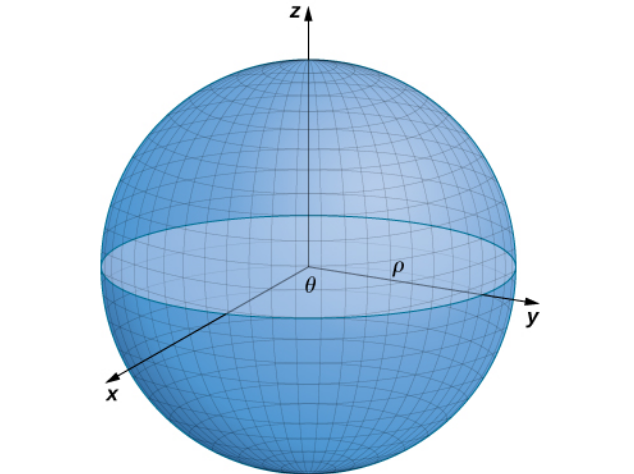
Example
Give a parameterization for the portion of cone $x^2 + y^2 = z^2$ lying in the first octant.
The surface can be described by the parameterization
$${\bf r}(r,\theta)=\langle r \cos \theta, r \sin \theta, r \rangle$$
where $\displaystyle 0 \leq \theta \lt \frac{\pi}{2}.$
Parameterizations of Surfaces Determined by Two-Variable Functions
$$ {\bf r}(x,y)=\langle x,y,f(x,y)\rangle $$
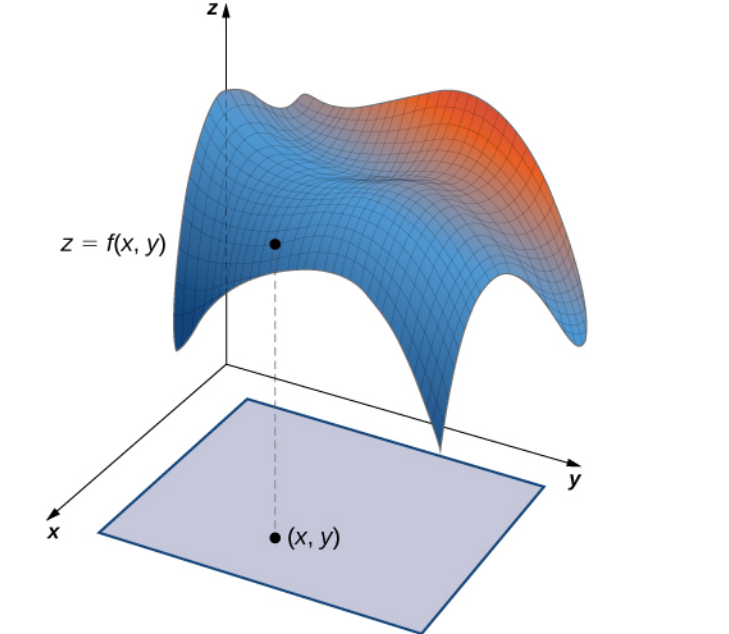
Note that since the name of the parameter doesn't matter, we will often see $x$ and $y$ used as parameters when parameterizing the surface determined by $f(x,y).$
Smooth Parameterizations
A surface parameterization ${\bf r}(s, t) = \langle x(s, t), y(s, t), z(s, t)\rangle$ is smooth if vector ${\bf r}_s \times {\bf r}_t$ is not zero for any choice of $s$ and $t$ in the parameter domain.
A surface is said to be piecewise smooth if it has smooth faces but also has locations where the directional derivatives do not exist.

As the terminology suggests, a smooth surface has not sharp corners where directional derivatives do not exist.
Example
Show that the parameterization of the paraboloid ${\bf r}(x,y)=\langle x,y,x^2+y^2\rangle$ is smooth.

For ${\bf r}(x,y)=\langle x,y,x^2+y^2\rangle,$ we have ${\bf r}_x=\langle 1,0,2x \rangle$ and ${\bf r}_y=\langle 0,1,2y \rangle,$ so that
$$
\begin{array}{lll}
\displaystyle {\bf r}_{x}\times {\bf r}_{y}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 1 & 0 & 2x \\ 0 & 1 & 2y \end{array}\right| &\mbox{}\\
\displaystyle &\displaystyle=(0-2x){\bf i}-(2y-0){\bf j}+(1-0){\bf k} &\mbox{}\\
\displaystyle &\displaystyle=-2x\,{\bf i}-2y\,{\bf j}+{\bf k} &\mbox{}\\
\displaystyle &\displaystyle=\langle -2x,-2y,1\rangle &\mbox{}\\
\end{array}
$$
Since ${\bf r}_{x}\times {\bf r}_{y}$ can never be the zero vector, the parameterization is smooth.
Surface Area
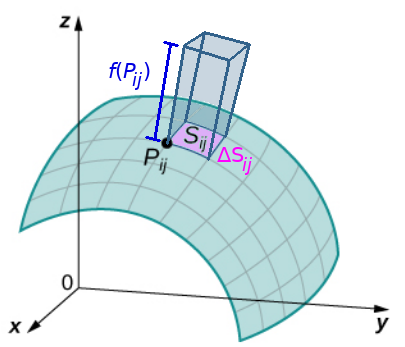
To determine the surface area of a region on the surface ${\bf r}(D)$ mapped to from a subset $D$ of the parameter domain, we impose a grid on $D$ and take $(s_i^*,t_j^*)$ to be the lower left corner of each $\Delta s$ by $\Delta t$ square $D_{ij}.$
We suppose that $P_{ij}={\bf r}(s_i^*,t_j^*)$ and ${\bf r}(D_{ij})=S_{ij}.$

Surface Area
To determine the surface area of a patch on the surface $S_{ij}$ mapped to from $D_{ij}$ we consider the tangent vectors $\displaystyle {\bf r}_s= \frac{\partial {\bf r}}{\partial s}=\left \langle\frac{\partial x}{\partial s},\frac{\partial y}{\partial s},\frac{\partial z}{\partial s}\right\rangle$ and $\displaystyle {\bf r}_t= \frac{\partial {\bf r}}{\partial t}=\left \langle\frac{\partial x}{\partial t},\frac{\partial y}{\partial t},\frac{\partial z}{\partial t}\right\rangle$ at
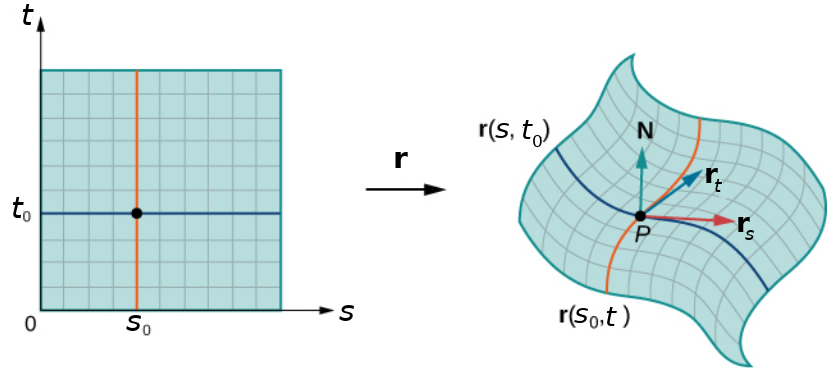
Surface Area
Recalling the notion of differentials, the change in ${\bf r}$ in the $s$ direction, $\Delta{\bf r}_s,$ is approximated by ${\bf r}_s\Delta s,$ and the change in ${\bf r}$ in the $t$ direction, $\Delta{\bf r}_t,$ is approximated by ${\bf r}_t\Delta t$.
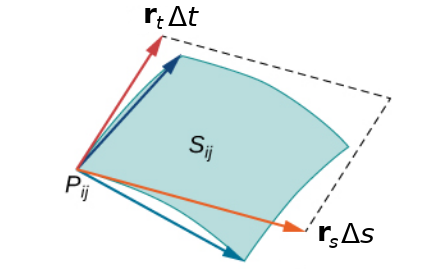
The area of the parallelogram formed by ${\bf r}_s\Delta s$ and ${\bf r}_t\Delta t$ approximates the area of $S_{ij}$ which we denote $\Delta S_{ij}.$
Surface Area
The surface area $\Delta S_{ij}$ of the patch $S_{ij}$ is the magnitude of the cross product of the vectors ${\bf r}_s\Delta s$ and ${\bf r}_t\Delta t$ That is, $$ \Delta S_{ij}\approx \Vert {\bf r}_s\Delta s \times {\bf r}_t\Delta t\Vert=\Vert{\bf r}_s \times {\bf r}_t\Vert\,\Delta s \, \Delta t $$

Surface Area
Summing over all $D_{ij},$ we get an approximation of the area of ${\bf r}(D).$ $$ \mbox{Surface Area}\approx \sum_{i=1}^{m}\sum_{j=1}^{n}\Delta S_{ij}\approx \sum_{i=1}^{m}\sum_{j=1}^{n}\Vert{\bf r}_s(P_{ij}) \times {\bf r}_t(P_{ij})\Vert\,\Delta s \, \Delta t $$


In the limit we have...
Surface Area
Summing over all $D_{ij},$ we get an approximation of the area of ${\bf r}(D).$ $$ \mbox{Surface Area} =\lim_{m,n \rightarrow \infty} \sum_{i=1}^{m}\sum_{j=1}^{n}\Vert{\bf r}_s(P_{ij}) \times {\bf r}_t(P_{ij})\Vert\,\Delta s \, \Delta t =\iint_D \, dS=\iint_D \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA $$


Example
Find the surface area of the paraboloid $z=x^2+y^2$ below $z=9.$

Since $z$ can be expressed as a function of $x$ and $y,$ we will parameterize the surface simply as ${\bf r}(x,y)=\langle x,y,x^2+y^2\rangle$
where $x^2+y^2\leq 9$
Then ${\bf r}_x=\langle 1,0,2x \rangle$ and ${\bf r}_y=\langle 0,1,2y \rangle,$ so that $$ \begin{array}{lll} \displaystyle {\bf r}_{x}\times {\bf r}_{y}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 1 & 0 & 2x \\ 0 & 1 & 2y \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-2x){\bf i}-(2y-0){\bf j}+(1-0){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=-2x\,{\bf i}-2y\,{\bf j}+{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\langle -2x,-2y,1\rangle &\mbox{}\\ \end{array} $$ We then have that $$ \left \Vert {\bf r}_x \times {\bf r}_y \right\Vert=\sqrt{(-2x)^2+(-2y)^2+1^2}=\sqrt{4x^2+4y^2+1} $$ The surface area is then $$ \begin{array}{lll} \displaystyle \iint_D \, dS&\displaystyle=\iint_D \left \Vert {\bf r}_x \times {\bf r}_y \right\Vert \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \sqrt{4x^2+4y^2+1} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr \, d\theta &\mbox{converting to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi} \, d\theta\right) \left(\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left(\int_{1}^{37} \sqrt{u} \cdot \frac{1}{8}\,du\right) &\mbox{letting $u=4r^2+1$ so that $\frac{1}{8}\,du=r \, dr$}\\ \displaystyle &\displaystyle=2\pi\cdot \frac{1}{8} \left(\int_{1}^{37} u^{1/2} \,du\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{4} \left[ \frac{2}{3}u^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{4} \cdot \frac{2}{3} \left[ u^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ 37^{3/2}-1^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ \left(\sqrt{37}\right)^3-1\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ 37\sqrt{37}-1\right] &\mbox{}\\ \displaystyle &\displaystyle\approx 117.3187007&\mbox{}\\ \end{array} $$
Then ${\bf r}_x=\langle 1,0,2x \rangle$ and ${\bf r}_y=\langle 0,1,2y \rangle,$ so that $$ \begin{array}{lll} \displaystyle {\bf r}_{x}\times {\bf r}_{y}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 1 & 0 & 2x \\ 0 & 1 & 2y \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-2x){\bf i}-(2y-0){\bf j}+(1-0){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=-2x\,{\bf i}-2y\,{\bf j}+{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\langle -2x,-2y,1\rangle &\mbox{}\\ \end{array} $$ We then have that $$ \left \Vert {\bf r}_x \times {\bf r}_y \right\Vert=\sqrt{(-2x)^2+(-2y)^2+1^2}=\sqrt{4x^2+4y^2+1} $$ The surface area is then $$ \begin{array}{lll} \displaystyle \iint_D \, dS&\displaystyle=\iint_D \left \Vert {\bf r}_x \times {\bf r}_y \right\Vert \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \sqrt{4x^2+4y^2+1} \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr \, d\theta &\mbox{converting to polar coordinates}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\left(\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi} \, d\theta\right) \left(\int_{0}^{3} \sqrt{4r^2+1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi \left(\int_{1}^{37} \sqrt{u} \cdot \frac{1}{8}\,du\right) &\mbox{letting $u=4r^2+1$ so that $\frac{1}{8}\,du=r \, dr$}\\ \displaystyle &\displaystyle=2\pi\cdot \frac{1}{8} \left(\int_{1}^{37} u^{1/2} \,du\right) &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{4} \left[ \frac{2}{3}u^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{4} \cdot \frac{2}{3} \left[ u^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ 37^{3/2}-1^{3/2}\right]_{1}^{37} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ \left(\sqrt{37}\right)^3-1\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{\pi}{6} \left[ 37\sqrt{37}-1\right] &\mbox{}\\ \displaystyle &\displaystyle\approx 117.3187007&\mbox{}\\ \end{array} $$
Act II
Scalar Surface Integrals
Scalar Surface Integrals
The above framework for determining the area on a parameterized surface sets up how we define surface integrals.
Scalar Surface Integrals
At each patch on the surface, $S_{ij},$ we multiply the surface area $\Delta S_{ij}$ by the value of a three-variable function $f(x,y,z)$ at the point $P_{ij}=(x(s_i^*,t_j^*),y(s_i^*,t_j^*),z(s_i^*,t_j^*)).$


Scalar Surface Integrals
The surface integral of a scalar-valued function $f$ over a piecewise smooth surface $S$ is $$ \iint_S f(x,y,z)\, dS=\lim_{m,n \rightarrow \infty}\sum_{i=1}^{m}\sum_{j=1}^{n} f(x(s_i^*,t_j^*),y(s_i^*,t_j^*),z(s_i^*,t_j^*)) \, \Delta S_{ij} $$


Interpretations
Surface integrals are like double integrals, except the region of integration is a "bumpy blanket" in space. So, we can think of surface integrals geometrically as weird volumes jutting out of surfaces.
Double integrals are essentially surface integrals of $f(x,y,0)$ over the surface $z=0.$ In this way, surface integrals are a generalization of double integrals.
Interpretations
Surface integrals can be applied to find weird volumes, but their main applications lie in physics. Some examples are given below.
If the function $f$ describes mass density at each point on the surface, then the surface integral is the total mass over a particular region.
If the function $f$ describes charge density at each point on the surface, then the surface integral is the total charge over a particular region.
Later, we shall look at a special case of surface integrals which will be an emphasis for the rest of this course. These kinds surface integrals lie at the heart the mathematical description of electromagnetic phenomena.
The surface integral definition given above is not easy to use.
Therefore, as with line integrals, we utilize a parameterization of a surface to evaluate surface integrals.
Scalar Surface Integrals
$$ \begin{array}{lll} \displaystyle \iint_S f(x,y,z)\, dS &\displaystyle =\lim_{m,n \rightarrow \infty}\sum_{i=1}^{m}\sum_{j=1}^{n} f(x(s_i^*,t_j^*),y(s_i^*,t_j^*),z(s_i^*,t_j^*)) \, \Delta S_{ij}\\ &\displaystyle=\lim_{m,n \rightarrow \infty} \sum_{i=1}^{m}\sum_{j=1}^{n}f\left({\bf r}(P_{ij})\right)\Vert{\bf r}_s(P_{ij}) \times {\bf r}_t(P_{ij})\Vert\,\Delta s \, \Delta t\\ &\displaystyle=\iint_D f\left({\bf r}(s,t)\right) \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA \end{array} $$


Comparing Scalar Line and Surface Integrals
$$ \displaystyle \int_C f(x,y)\, ds=\int_a^b f({\bf r}(t))\, \Vert {\bf r}'(t)\Vert \,dt $$ $$ \iint_S f(x,y,z)\, dS=\iint_D f\left({\bf r}(s,t)\right) \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA $$
Example
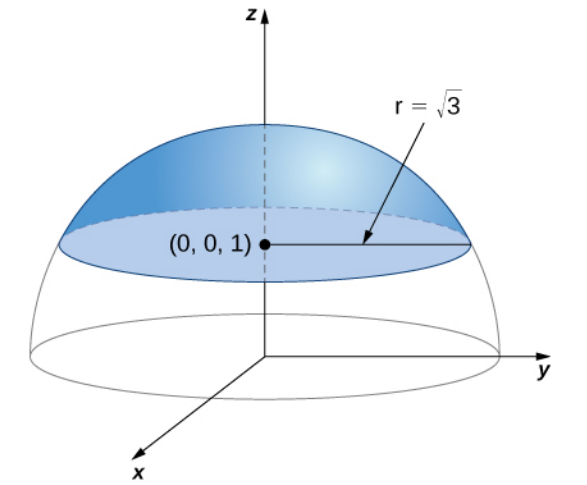
Calculate surface integral $\displaystyle \iint_S z^2\,dS,$ $S$ is the surface that consists of the piece of sphere $x^2 + y^2 + z^2 = 4$ that lies on or above plane $z = 1.$
We'll use the standard parameterization of the sphere.
However, instead of using $s$ and $t$ as parameters, we'll use $\phi$ and $\theta.$
The sphere of radius $2$ is parameterized as $$ {\bf r}(\phi, \theta) = \langle 2 \cos \theta \sin \phi, 2 \sin \theta \sin \phi, 2 \cos \phi \rangle $$ over $0 \leq \theta \leq 2\pi$ and $0 \leq \phi \leq \phi_0$ where $\phi_0$ is to be determined based upon information given by the problem.

From the figure we see that $\displaystyle \sin \phi_0 = \frac{\sqrt{3}}{2}.$
Then $\displaystyle \phi_0=\frac{\pi}{3}.$
It follows that $\displaystyle 0 \leq \phi \leq \frac{\pi}{3}.$
We may now begin to set up our surface integral.
First we note that ${\bf r}_{\phi}=\langle 2 \cos \theta \cos \phi, 2 \sin \theta \cos \phi, -2 \sin \phi \rangle$ and ${\bf r}_{\theta}\langle -2 \sin \theta \sin \phi, 2 \cos \theta \sin \phi, 0 \rangle.$
Now we compute ${\bf r}_{\phi}\times {\bf r}_{\theta}.$ $$ \begin{array}{lll} \displaystyle {\bf r}_{\phi}\times {\bf r}_{\theta}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 2 \cos \theta \cos \phi & 2 \sin \theta \cos \phi & -2 \sin \phi \\ -2 \sin \theta \sin \phi & 2 \cos \theta \sin \phi & 0 \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-(-4\cos\theta \sin^2 \phi)){\bf i}-(0-4\sin \theta \sin^2 \phi){\bf j}+(4\cos^2 \theta \cos \phi \sin \phi+4\sin^2\theta \cos \phi \sin \phi){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=4\cos\theta \sin^2 \phi\,{\bf i}+4\sin \theta \sin^2 \phi\,{\bf j}+4(\cos^2 \theta +\sin^2\theta)\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=4\cos\theta \sin^2 \phi\,{\bf i}+4\sin \theta \sin^2 \phi\,{\bf j}+4\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle \Vert {\bf r}_{\phi}\times {\bf r}_{\theta} \Vert&\displaystyle=\sqrt{(4\cos\theta \sin^2 \phi)^2+(4\sin \theta \sin^2 \phi)^2+(4\cos \phi \sin \phi)^2}&\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\cos^2 \theta \sin^4 \phi+16\sin^2 \theta \sin^4 \phi+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi (\cos^2 \theta +\sin^2 \theta)+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi (\cos^2 \theta +\sin^2 \theta)+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi +16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^4 \phi +\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^2 \phi(\sin^2 \phi +\cos^2 \phi)} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4|\sin \phi| &\mbox{}\\ \displaystyle &\displaystyle=4\sin \phi &\mbox{since $\displaystyle 0 \leq \phi \leq \frac{\pi}{3}$}\\ \end{array} $$ The integral is then $$ \begin{array}{lll} \displaystyle \iint_S z^2 \, dS&\displaystyle=\iint_D z(\phi,\theta)^2 \left \Vert {\bf r}_{\phi}\times {\bf r}_{\theta} \right\Vert \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D (2 \cos \phi)^2\cdot 4\sin \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 16 \cos^2 \phi\, \sin \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=16\int_{0}^{2\pi}\left(\int_{0}^{\pi/3} \cos^2 \phi\, \sin \phi \, d\phi\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=16\left(\int_{0}^{2\pi} \, d\theta\right) \left(\int_{0}^{\pi/3} \cos^2 \phi\, \sin \phi \, d\phi\right) &\mbox{}\\ \displaystyle &\displaystyle=16\cdot 2\pi \left[-\frac{1}{3}\cos^3 \phi \right]_{0}^{\pi/3} &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\cos^3\left(\frac{\pi}{3}\right)-\left(-\frac{1}{3}\cos^3(0)\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\left(\frac{1}{2}\right)^3-\left(-\frac{1}{3}\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\left(\frac{1}{8}\right) + \frac{1}{3} \right] &\mbox{}\\ \displaystyle &\displaystyle=-\frac{1}{3}\left(\frac{32\pi}{8}\right) + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{1}{3}(4\pi) + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{4\pi}{3} + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{28\pi}{3} &\mbox{}\\ \end{array} $$
However, instead of using $s$ and $t$ as parameters, we'll use $\phi$ and $\theta.$
The sphere of radius $2$ is parameterized as $$ {\bf r}(\phi, \theta) = \langle 2 \cos \theta \sin \phi, 2 \sin \theta \sin \phi, 2 \cos \phi \rangle $$ over $0 \leq \theta \leq 2\pi$ and $0 \leq \phi \leq \phi_0$ where $\phi_0$ is to be determined based upon information given by the problem.

From the figure we see that $\displaystyle \sin \phi_0 = \frac{\sqrt{3}}{2}.$
Then $\displaystyle \phi_0=\frac{\pi}{3}.$
It follows that $\displaystyle 0 \leq \phi \leq \frac{\pi}{3}.$
We may now begin to set up our surface integral.
First we note that ${\bf r}_{\phi}=\langle 2 \cos \theta \cos \phi, 2 \sin \theta \cos \phi, -2 \sin \phi \rangle$ and ${\bf r}_{\theta}\langle -2 \sin \theta \sin \phi, 2 \cos \theta \sin \phi, 0 \rangle.$
Now we compute ${\bf r}_{\phi}\times {\bf r}_{\theta}.$ $$ \begin{array}{lll} \displaystyle {\bf r}_{\phi}\times {\bf r}_{\theta}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 2 \cos \theta \cos \phi & 2 \sin \theta \cos \phi & -2 \sin \phi \\ -2 \sin \theta \sin \phi & 2 \cos \theta \sin \phi & 0 \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-(-4\cos\theta \sin^2 \phi)){\bf i}-(0-4\sin \theta \sin^2 \phi){\bf j}+(4\cos^2 \theta \cos \phi \sin \phi+4\sin^2\theta \cos \phi \sin \phi){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=4\cos\theta \sin^2 \phi\,{\bf i}+4\sin \theta \sin^2 \phi\,{\bf j}+4(\cos^2 \theta +\sin^2\theta)\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=4\cos\theta \sin^2 \phi\,{\bf i}+4\sin \theta \sin^2 \phi\,{\bf j}+4\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle \Vert {\bf r}_{\phi}\times {\bf r}_{\theta} \Vert&\displaystyle=\sqrt{(4\cos\theta \sin^2 \phi)^2+(4\sin \theta \sin^2 \phi)^2+(4\cos \phi \sin \phi)^2}&\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\cos^2 \theta \sin^4 \phi+16\sin^2 \theta \sin^4 \phi+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi (\cos^2 \theta +\sin^2 \theta)+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi (\cos^2 \theta +\sin^2 \theta)+16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=\sqrt{16\sin^4 \phi +16\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^4 \phi +\cos^2 \phi \sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^2 \phi(\sin^2 \phi +\cos^2 \phi)} &\mbox{}\\ \displaystyle &\displaystyle=4\sqrt{\sin^2 \phi} &\mbox{}\\ \displaystyle &\displaystyle=4|\sin \phi| &\mbox{}\\ \displaystyle &\displaystyle=4\sin \phi &\mbox{since $\displaystyle 0 \leq \phi \leq \frac{\pi}{3}$}\\ \end{array} $$ The integral is then $$ \begin{array}{lll} \displaystyle \iint_S z^2 \, dS&\displaystyle=\iint_D z(\phi,\theta)^2 \left \Vert {\bf r}_{\phi}\times {\bf r}_{\theta} \right\Vert \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D (2 \cos \phi)^2\cdot 4\sin \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 16 \cos^2 \phi\, \sin \phi \, dA &\mbox{}\\ \displaystyle &\displaystyle=16\int_{0}^{2\pi}\left(\int_{0}^{\pi/3} \cos^2 \phi\, \sin \phi \, d\phi\right) \, d\theta &\mbox{}\\ \displaystyle &\displaystyle=16\left(\int_{0}^{2\pi} \, d\theta\right) \left(\int_{0}^{\pi/3} \cos^2 \phi\, \sin \phi \, d\phi\right) &\mbox{}\\ \displaystyle &\displaystyle=16\cdot 2\pi \left[-\frac{1}{3}\cos^3 \phi \right]_{0}^{\pi/3} &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\cos^3\left(\frac{\pi}{3}\right)-\left(-\frac{1}{3}\cos^3(0)\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\left(\frac{1}{2}\right)^3-\left(-\frac{1}{3}\right) \right] &\mbox{}\\ \displaystyle &\displaystyle=32\pi\left[-\frac{1}{3}\left(\frac{1}{8}\right) + \frac{1}{3} \right] &\mbox{}\\ \displaystyle &\displaystyle=-\frac{1}{3}\left(\frac{32\pi}{8}\right) + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{1}{3}(4\pi) + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=-\frac{4\pi}{3} + \frac{32\pi}{3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{28\pi}{3} &\mbox{}\\ \end{array} $$
Surface Integrals Over Surfaces Given by $z=g(x,y).$
Recall that we may parameterize a surface given by $z=g(x,y)$ as ${\bf r}(x,y)=\langle x,y,g(x,y)\rangle.$

Surface Integrals Over Surfaces Given by $z=g(x,y).$ $$ \begin{array}{lll} \displaystyle \iint_S f(x,y,z)\, dS &\displaystyle=\iint_D f\left({\bf r}(x,y)\right) \left \Vert {\bf r}_x \times {\bf r}_y \right\Vert \, dA\\ &\displaystyle=\iint_D f\left(x,y,g(x,y)\right) \left \Vert \left| \begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 1&0&g_x \\ 0&1&g_y\end{array} \right| \right \Vert \, dA\\ &\displaystyle=\iint_D f\left(x,y,g(x,y)\right) \left \Vert \langle -g_x ,-g_y, 1 \rangle \right \Vert \, dA\\ &\displaystyle=\iint_D f\left(x,y,g(x,y)\right) \sqrt{g_x^2+g_y^2+1} \, dA\\ \end{array} $$
Application: Mass From Density
A flat sheet of metal has the shape of surface $z = 1 + x + 2y$ that lies above rectangle $0 \leq x \leq 4$ and $0 \leq y \leq 2.$
If the density of the sheet is given by $\rho(x, y, z) = x^2 yz,$ what is the mass of the sheet?
The mass is given by the surface integral
$$
\iint_S \rho(x,y,z)\, dS
$$
We shall use the formula for a surface integral over a surface given by $z=g(x,y)$ to find the mass.
$$
\begin{array}{lll}
\displaystyle \iint_S \rho(x,y,z)\, dS &\displaystyle=\iint_D \rho\left(x,y,g(x,y)\right) \sqrt{g_x^2+g_y^2+1} \, dA &\mbox{}\\
\displaystyle &\displaystyle=\iint_D \rho\left(x,y,1+x+2y\right) \sqrt{(1)^2+(2)^2+1} \, dA &\mbox{since $g(x,y)=1+x+2y$}\\
\displaystyle &\displaystyle=\iint_D x^2y(1+x+2y) \sqrt{6} \, dA &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6} \iint_D x^2y+x^3y+2x^2y^2 \, dA &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6} \int_{0}^{4}\int_{0}^{2} x^2y+x^3y+2x^2y^2 \, dy\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\int_{0}^{4} \left[x^2\cdot \frac{1}{2}y^2+x^3\cdot \frac{1}{2}y^2+2x^2\cdot \frac{1}{3}y^3\right]_{0}^{2}\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\int_{0}^{4} \left[\frac{1}{2}x^2y^2+\frac{1}{2}x^3y^2+\frac{2}{3}x^2y^3\right]_{0}^{2}\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\int_{0}^{4} \frac{1}{2}x^2(2^2)+\frac{1}{2}x^3(2^2)+\frac{2}{3}x^2(2^3)\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\int_{0}^{4} 2x^2+2x^3+\frac{16}{3}x^2\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\int_{0}^{4} \frac{22}{3}x^2+2x^3\,dx &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\left[\frac{22}{9}x^3+\frac{1}{2}x^4\right]_{0}^{4} &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\left(\frac{22}{9}(4^3)+\frac{1}{2}(4^4)\right) &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\left(\frac{1408}{9}+128\right) &\mbox{}\\
\displaystyle &\displaystyle=\sqrt{6}\cdot\frac{2560}{9} &\mbox{}\\
\displaystyle &\displaystyle=\frac{2560\sqrt{6}}{9} &\mbox{}\\
\displaystyle &\displaystyle\approx 696.7437491 &\mbox{}\\
\end{array}
$$
Act III
Vector Surface Integrals
(Flux Integrals)
Vector Surface Integrals
(Flux Integrals)
Flux Integrals in $\mathbb{R}^3$
With two-dimensional flux integrals we quantified how much a two-dimensional vector field "flows through" a curve.
We now immerse surfaces in a three-dimensional vector fields to understand how much a field "flows through" that surface.
Before we do this, however, we must "orient" the surface just as we did for curves.
Sometimes this is possible, other times it isn't...
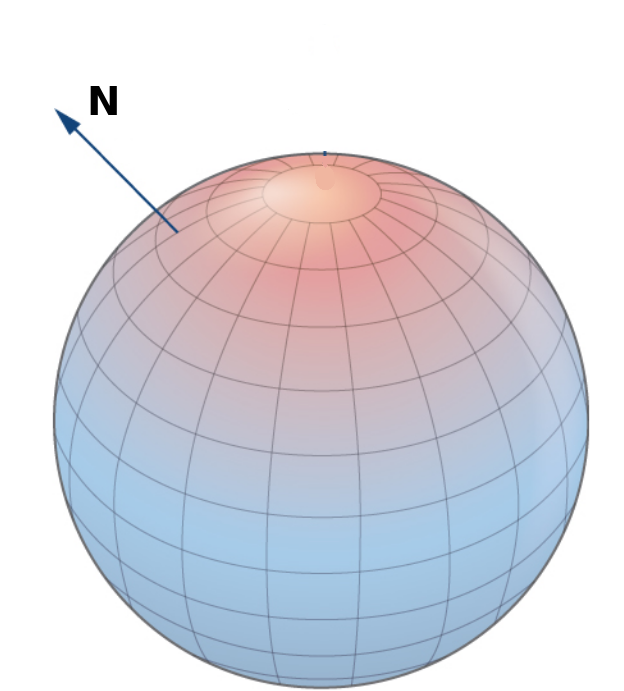
Orientation of a Surface
On any surface well-behaved surface, we can find two unit normal vectors ${\bf N}$ and $-{\bf N}$
Which of these we choose determines the orientation.
 |  |  |
| Upward/Downward | Inward/Outward | Inward/Outward |
As long as a surface has an "upper side" and "lower side," or an "outer side" and "inner side," the surface is said to be orientable.
Non-Orientable Surfaces
Some surfaces do not have an upper or lower, or inner or outer side.
The most common example of a non-orientable surface is the Möbius band.

Since this surface is one-sided, there is no way to distinguish one side from another.
We will consider only orientable surfaces for this course.
Flux Through a Surface
The flux of a three-dimensional vector field ${\bf F}$ through a surface $S$ is the degree to which the field "flows through" that surface.
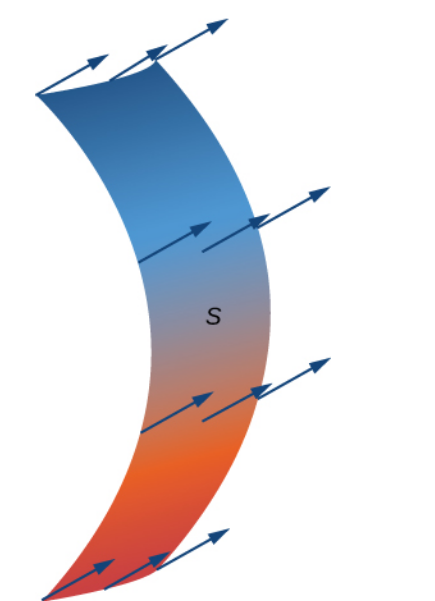
Flux Through a Surface
Although flux models many different phenomena, to keep a concrete example firmly in mind, we shall imagine flux as the amount of some fluid flowing through a permeable surface, such as water flowing through a net.

Flux Through a Surface
We shall consider a "tiny patch" $S_{ij}$ of our surface, small enough so that the velocity field ${\bf F}$ at all points near $P_{ij}$ is roughly constant.
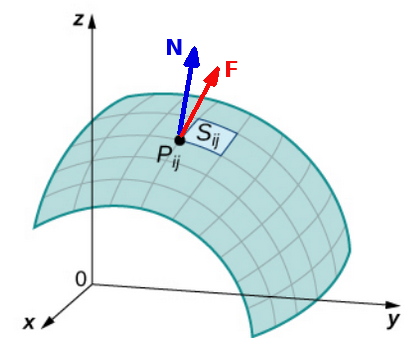
Flux Through a Surface
The amount of fluid per passing through $S_{ij}$ per unit time is approximately the velocity ${\bf F}$ of the fluid in the direction of the unit normal vector ${\bf N}$ times the area of the patch $\Delta S_{ij}.$
Since the velocity of the fluid in the direction of the unit normal is precisely ${\bf F}\cdot {\bf N},$ we have $$ \mbox{Flux through $S_{ij}$}\approx {\bf F}(P_{ij})\cdot{\bf N}(P_{ij})\,\Delta S_{ij} $$

Flux Through a Surface
Summing over all the "tiny patches" $S_{ij},$ $$ \mbox{Flux through $S$} \approx \sum_{i=1}^{m}\sum_{j=1}^{n}{\bf F}(P_{ij})\cdot{\bf N}(P_{ij})\,\Delta S_{ij} $$

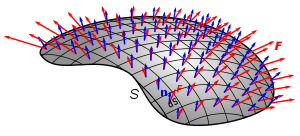
Flux Through a Surface
In the limit, we obtain the exact flux. $$ \mbox{Flux through $S$} =\lim_{m,n \rightarrow \infty} \sum_{i=1}^{m}\sum_{j=1}^{n}{\bf F}(P_{ij})\cdot{\bf N}(P_{ij})\,\Delta S_{ij} =\iint_S {\bf F}\cdot {\bf N} \, dS $$


Another Notation for Flux Integrals
We may interpret ${\bf N} \, dS$ as the differential vector quantity $d{\bf S}$ so that we may write $\displaystyle \iint_S {\bf F}\cdot {\bf N} \, dS$ as $$ \iint_S {\bf F}\cdot \, d{\bf S} $$
Note that this notation is similar to $\displaystyle \int_C {\bf F} \cdot \, d{\bf r}$ for line integrals.
Evalulating Flux Integrals
Having a parameterization of our surface $S$ makes evaluating flux integrals substantially easier than using the above definitions.
In order to utilize a parameterization, we need an explicit expression for the normal vector ${\bf N}$ at an arbitrary point on the surface.
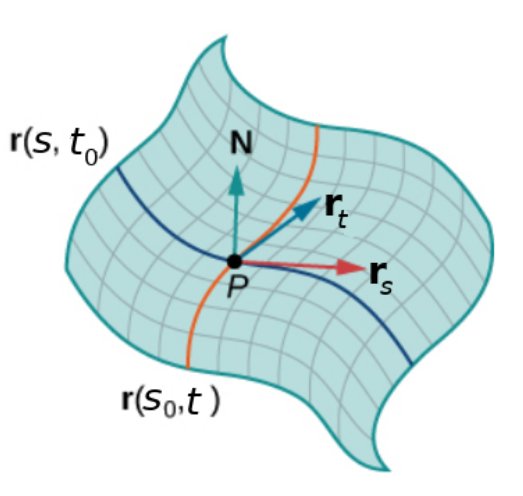
We begin by again considering the tangent vectors ${\bf r}_s$ and ${\bf r}_t$ on our surface $S.$

Evalulating Flux Integrals
From ${\bf r}_s$ and ${\bf r}_t$ a normal vector is obtained by taking the cross product $${\bf r}_s \times {\bf r}_t$$ Dividing the above by the its magnitude we get a unit normal ${\bf N}$ at an arbitrary point on the surface. $$ {\bf N}({\bf r}(s,t))=\frac{{\bf r}_s \times {\bf r}_t}{\Vert{\bf r}_s \times {\bf r}_t\Vert} $$

Evalulating Flux Integrals
We now have everything we need to evaluate a flux integral. $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot d{\bf S} &=\displaystyle \iint_S {\bf F}\cdot {\bf N} \, dS&\mbox{}\\ &=\displaystyle \iint_D {\bf F}({\bf r}(s,t))\cdot {\bf N}({\bf r}(s,t)) \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA&\mbox{}\\ &=\displaystyle \iint_D {\bf F}({\bf r}(s,t))\cdot \frac{{\bf r}_s \times {\bf r}_t}{\left \Vert {\bf r}_s \times {\bf r}_t \right\Vert} \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA&\mbox{}\\ &=\displaystyle \iint_D {\bf F}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA&\mbox{}\\ \end{array} $$
Analogies
Note the similarities between the two formulas for the line integral over a parameterized curve $C,$ $$ \int_C {\bf F}\cdot d{\bf r}=\int_{a}^{b} {\bf F}({\bf r}(t))\cdot {\bf r}'(t) \,dt $$ and the formula for the surface flux integral over a parameterized surface $S,$ $$ \iint_S {\bf F}\cdot d{\bf S}= \iint_D {\bf F}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA $$
Example
Find the flux of the vector field ${\bf F} = x^2{\bf i}+y^2{\bf j}+z^2{k}$ through the surface $S$ which consists of the cylinder $x^2 + y^2 = 1,$ $-1 \leq z \leq 1.$ Assume this surface is positively (outwardly) oriented.
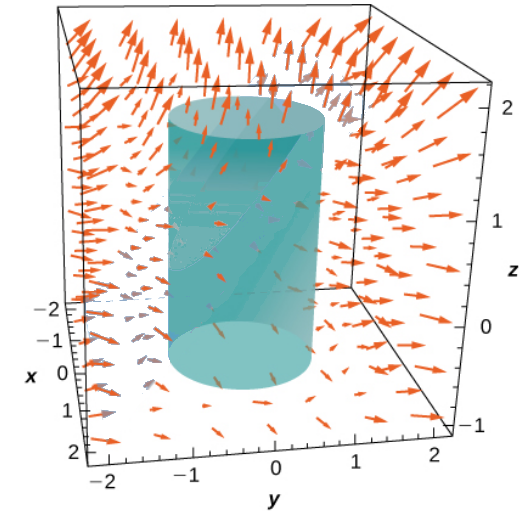
We first parameterize the cylinder as ${\bf r}(s,t)=\langle \cos s,\sin s, t\rangle$ with $0 \leq s \leq 2\pi$ and $-1 \leq t \leq 1.$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle -\sin s & \cos s & 0 \\ 0 & 0 & 1\end{array}\right|\\ &=(\cos s-0){\bf i}-(-\sin s-0){\bf j}+(0-0){\bf k}\\ &=\cos s{\bf i}+\sin s{\bf j}+0{\bf k}\\ &=\langle \cos s,\sin s,0\rangle\\ \end{array} $$ We may now calculate our flux integral. $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot d{\bf S}&\displaystyle= \iint_D {\bf F}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D \langle x(s,t)^2,y(s,t)^2,z(s,t)^2, \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \langle \cos^2 s,\sin^2 s,t^2 \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D (\cos^2 s)(\cos s) +(\sin^2 s)(\sin s)+(t^2)(0) \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \cos^3 s +\sin^3 s \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-1}^{1} \int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-1}^{1} \left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right)\, dt &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{-1}^{1} \, dt\right)\left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right) &\mbox{}\\ \displaystyle &\displaystyle=2\left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right) &\mbox{}\\ \displaystyle &\displaystyle=2\left[ \frac{1}{3}\left(2+\cos^2 s\right)\sin s -\frac{1}{3}\left(2+\sin^2 s\right)\cos s\right]_{0}^{2\pi} &\mbox{table of integrals!}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[ \left(2+\cos^2 s\right)\sin s -\left(2+\sin^2 s\right)\cos s\right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[\left(2+\cos^2 (2\pi)\right)\sin (2\pi) -\left(2+\sin^2 (2\pi)\right)\cos (2\pi) -\left(\left(2+\cos^2(0)\right)\sin(0) -\left(2+\sin^2(0) \right)\cos (0)\right)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[\left(2+1^2\right)\cdot 0 -\left(2+0^2\right)\cdot 1 -\left(\left(2+1^2\right)\cdot 0 -\left(2+0^2 \right)\cdot 1\right)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[ -2 -( -2)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[0\right] &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
Then $$ \begin{array}{ll} {\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle -\sin s & \cos s & 0 \\ 0 & 0 & 1\end{array}\right|\\ &=(\cos s-0){\bf i}-(-\sin s-0){\bf j}+(0-0){\bf k}\\ &=\cos s{\bf i}+\sin s{\bf j}+0{\bf k}\\ &=\langle \cos s,\sin s,0\rangle\\ \end{array} $$ We may now calculate our flux integral. $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot d{\bf S}&\displaystyle= \iint_D {\bf F}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D \langle x(s,t)^2,y(s,t)^2,z(s,t)^2, \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \langle \cos^2 s,\sin^2 s,t^2 \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D (\cos^2 s)(\cos s) +(\sin^2 s)(\sin s)+(t^2)(0) \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D \cos^3 s +\sin^3 s \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{-1}^{1} \int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\, dt &\mbox{}\\ \displaystyle &\displaystyle=\int_{-1}^{1} \left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right)\, dt &\mbox{}\\ \displaystyle &\displaystyle=\left(\int_{-1}^{1} \, dt\right)\left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right) &\mbox{}\\ \displaystyle &\displaystyle=2\left(\int_{0}^{2\pi} \cos^3 s +\sin^3 s \, ds\right) &\mbox{}\\ \displaystyle &\displaystyle=2\left[ \frac{1}{3}\left(2+\cos^2 s\right)\sin s -\frac{1}{3}\left(2+\sin^2 s\right)\cos s\right]_{0}^{2\pi} &\mbox{table of integrals!}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[ \left(2+\cos^2 s\right)\sin s -\left(2+\sin^2 s\right)\cos s\right]_{0}^{2\pi} &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[\left(2+\cos^2 (2\pi)\right)\sin (2\pi) -\left(2+\sin^2 (2\pi)\right)\cos (2\pi) -\left(\left(2+\cos^2(0)\right)\sin(0) -\left(2+\sin^2(0) \right)\cos (0)\right)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[\left(2+1^2\right)\cdot 0 -\left(2+0^2\right)\cdot 1 -\left(\left(2+1^2\right)\cdot 0 -\left(2+0^2 \right)\cdot 1\right)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[ -2 -( -2)\right] &\mbox{}\\ \displaystyle &\displaystyle=\frac{2}{3}\left[0\right] &\mbox{}\\ \displaystyle &\displaystyle=0 &\mbox{}\\ \end{array} $$
Flux Integrals Over Surfaces Given by $z=g(x,y)$ Oriented Upward
If ${\bf F}=\langle P,Q,R \rangle$ and our surface $S$ is parameterized as ${\bf r}(x,y)=\langle x,y,g(x,y)\rangle,$ then $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S} &\displaystyle=\iint_D {\bf F}(\left({\bf r}(x,y)\right) \cdot ({\bf r}_x \times {\bf r}_y ) \, dA\\ &\displaystyle=\iint_D {\bf F}\left(x,y,g(x,y)\right)\cdot \left| \begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ 1&0&g_x \\ 0&1&g_y\end{array} \right| \, dA\\ &\displaystyle=\iint_D \left \langle P(x,y,g(x,y)),Q(x,y,g(x,y)_,R(x,y,g(x,y))\right\rangle \cdot \left \langle -g_x ,-g_y, 1 \right \rangle \, dA\\ &\displaystyle=\iint_D -P(x,y,g(x,y))g_x-Q(x,y,g(x,y))g_y+R(x,y,g(x,y)) \, dA\\ &\displaystyle=\iint_D -Pg_x-Q g_y+R \, dA\\ \end{array} $$
Example
Find the flux of the vector field ${\bf F} = x^2{\bf i}+y^2{\bf j}+z^2{k}$ through the top and bottom of the cylinder from the previous example $x^2 + y^2 = 1,$ $-1 \leq z \leq 1.$
Assume the top is oriented upward and the bottom is oriented downward.

We use the formula for the flux through a surface given by a function $z=g(x,y).$
For the top surface $T,$ we'll take $z=g(x,y)=1.$ Then $$ \begin{array}{lll} \displaystyle \iint_T {\bf F}\cdot\, d{\bf S}&\displaystyle= \iint_D -Pg_x-Q g_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D -x^2 \cdot 0 -y^2 \cdot 0+z^2 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 1^2 \, dA &\mbox{since $z=g(x,y)=1$}\\ \displaystyle &\displaystyle=\iint_D \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{1} \, r \, dr \, d\theta &\mbox{in polar coordinates}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi} \, d\theta\right)\left(\int_{0}^{1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[ \frac{1}{2}r^2\right]_{0}^{1} &\mbox{}\\ \displaystyle &\displaystyle=2\pi\cdot \frac{1}{2} &\mbox{}\\ \displaystyle &\displaystyle=\pi&\mbox{}\\ \end{array} $$
For the bottom we'll take the surface $B$ to be $z=h(x,y)=1.$
However, we must append a negative sign to the integral since the surface will be oriented downward. $$ \begin{array}{lll} \displaystyle \iint_B {\bf F}\cdot\, d{\bf S}&\displaystyle= -\left(\iint_D -Ph_x-Q h_y+R \, dA\right)&\mbox{}\\ \displaystyle &\displaystyle= \iint_D Ph_x+Q h_y-R \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D x^2 \cdot 0 +y^2 \cdot 0-z^2 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D -(-1)^2 \, dA &\mbox{since $z=h(x,y)=-1$}\\ \displaystyle &\displaystyle=\iint_D -1\, dA &\mbox{}\\ \displaystyle &\displaystyle=-\iint_D \, dA &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi}\int_{0}^{1} \, r \, dr \, d\theta &\mbox{in polar coordinates}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{2\pi} \, d\theta\right)\left(\int_{0}^{1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=-2\pi\left[ \frac{1}{2}r^2\right]_{0}^{1} &\mbox{}\\ \displaystyle &\displaystyle=-2\pi\cdot \frac{1}{2} &\mbox{}\\ \displaystyle &\displaystyle=-\pi&\mbox{}\\ \end{array} $$
For the top surface $T,$ we'll take $z=g(x,y)=1.$ Then $$ \begin{array}{lll} \displaystyle \iint_T {\bf F}\cdot\, d{\bf S}&\displaystyle= \iint_D -Pg_x-Q g_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D -x^2 \cdot 0 -y^2 \cdot 0+z^2 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D 1^2 \, dA &\mbox{since $z=g(x,y)=1$}\\ \displaystyle &\displaystyle=\iint_D \, dA &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{2\pi}\int_{0}^{1} \, r \, dr \, d\theta &\mbox{in polar coordinates}\\ \displaystyle &\displaystyle=\left(\int_{0}^{2\pi} \, d\theta\right)\left(\int_{0}^{1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=2\pi\left[ \frac{1}{2}r^2\right]_{0}^{1} &\mbox{}\\ \displaystyle &\displaystyle=2\pi\cdot \frac{1}{2} &\mbox{}\\ \displaystyle &\displaystyle=\pi&\mbox{}\\ \end{array} $$
For the bottom we'll take the surface $B$ to be $z=h(x,y)=1.$
However, we must append a negative sign to the integral since the surface will be oriented downward. $$ \begin{array}{lll} \displaystyle \iint_B {\bf F}\cdot\, d{\bf S}&\displaystyle= -\left(\iint_D -Ph_x-Q h_y+R \, dA\right)&\mbox{}\\ \displaystyle &\displaystyle= \iint_D Ph_x+Q h_y-R \, dA&\mbox{}\\ \displaystyle &\displaystyle=\iint_D x^2 \cdot 0 +y^2 \cdot 0-z^2 \, dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D -(-1)^2 \, dA &\mbox{since $z=h(x,y)=-1$}\\ \displaystyle &\displaystyle=\iint_D -1\, dA &\mbox{}\\ \displaystyle &\displaystyle=-\iint_D \, dA &\mbox{}\\ \displaystyle &\displaystyle=-\int_{0}^{2\pi}\int_{0}^{1} \, r \, dr \, d\theta &\mbox{in polar coordinates}\\ \displaystyle &\displaystyle=-\left(\int_{0}^{2\pi} \, d\theta\right)\left(\int_{0}^{1} \, r \, dr\right) &\mbox{}\\ \displaystyle &\displaystyle=-2\pi\left[ \frac{1}{2}r^2\right]_{0}^{1} &\mbox{}\\ \displaystyle &\displaystyle=-2\pi\cdot \frac{1}{2} &\mbox{}\\ \displaystyle &\displaystyle=-\pi&\mbox{}\\ \end{array} $$
Example
Find the flux of the vector field ${\bf F} = \langle x - y, x + z, z - y \rangle$ through the surface $S$ which consists of the cone $x^2 + y^2 = z^2,$ $0 \leq z \leq 1,$ and the circular top of the cone. Assume this surface is positively (outwardly) oriented.

We will calculate the flux through surfaces $z=g(x,y)=\sqrt{x^2+y^2}$ and $z=h(x,y)=1,$
both over the region $D=\{(x,y)\in \mathbb{R}^2|x^2+y^2\leq 1\}.$
We let $C$ be the cone and $P$ be the plane which make up our piecewise-smooth, closed surface $S$.
Thus $S$ can be expressed as $C \cup P.$
Now, for the closed surface to be positively (outwardly) oriented, the normal vector on the cone must point outward.
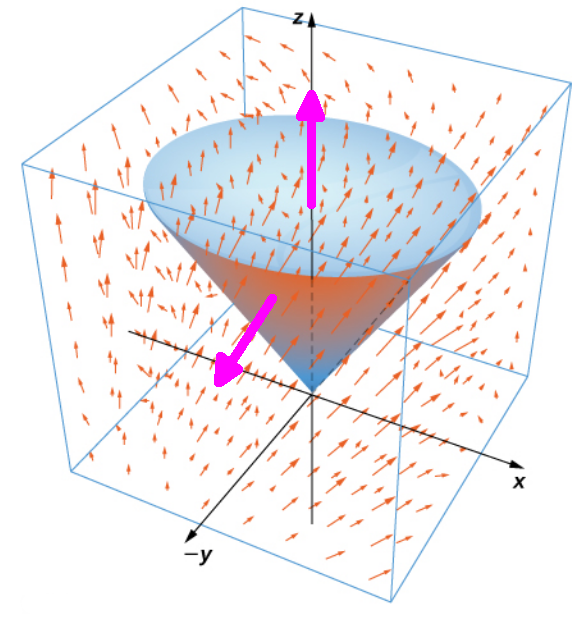
That is, we must orient the surface $C$ negatively.
The above leads us to $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iint_{C \cup P} {\bf F}\cdot\, d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{C} {\bf F}\cdot\, d{\bf S}+\iint_P {\bf F}\cdot\, d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle= -\left(\iint_D -Pg_x-Q g_y+R \, dA\right)+\iint_D -Ph_x-Q h_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D Pg_x+Q g_y-R \, dA+\iint_D -Ph_x-Q h_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + z)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(z-y) \, dA+\iint_D -(x-y)\cdot 0-(x+z)\cdot 0+(z-y) \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + z)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(z-y) \, dA+\iint_D z-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + \color{magenta}{g(x,y)})\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(\color{magenta}{g(x,y)}-y) \, dA+\iint_D \color{magenta}{h(x,y)}-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+\left(x + \color{magenta}{\sqrt{x^2+y^2}}\right)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -\left(\color{magenta}{\sqrt{x^2+y^2}}-y\right) \, dA+\iint_D \color{magenta}{1}-y \, dA&\mbox{}\\ %\displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+\left(x + \sqrt{x^2+y^2}\right)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -\left(1-y\right) \, dA+\iint_D \sqrt{x^2+y^2}-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}}-\frac{xy}{\sqrt{x^2+y^2}}+\frac{xy}{\sqrt{x^2+y^2}}+y -\sqrt{x^2+y^2}+y \, dA+\iint_D 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+2y \, dA+\iint_D 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+2y + 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+y + 1 \, dA&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\int_{0}^{1} \left(\frac{r^2\cos^2 \theta}{r}-r +r\sin \theta +1\right) \, r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\int_{0}^{1} r^2\cos^2 \theta-r^2 + r^2\sin \theta +r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\left[\frac{1}{3}r^3\cos^2 \theta-\frac{1}{3}r^3 + \frac{1}{3}r^3\sin \theta +\frac{1}{2}r^2\right]_{0}^{1}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\frac{1}{3}\cos^2 \theta-\frac{1}{3} + \frac{1}{3}\sin \theta +\frac{1}{2}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\frac{1}{3}\cos^2 \theta + \frac{1}{3}\sin \theta +\frac{1}{6}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{3}\left(\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta)\right) - \frac{1}{3}\cos \theta +\frac{1}{6}\theta\right]_{0}^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= \left[\left(\frac{1}{6}\theta+\frac{1}{12}\sin(2\theta)\right) - \frac{1}{3}\cos \theta +\frac{1}{6}\theta\right]_{0}^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= \left(\frac{1}{6}(2\pi)+\frac{1}{12}\sin(4\pi)\right) - \frac{1}{3}\cos(2\pi) +\frac{1}{6}(2\pi)-\left(\left(\frac{1}{6}(0)+\frac{1}{12}\sin(0)\right) - \frac{1}{3}\cos 0 +\frac{1}{6}(0)\right)&\mbox{}\\ \displaystyle &\displaystyle= \left(\frac{\pi}{3}+0\right) - \frac{1}{3} +\frac{\pi}{3}-\left(0 - \frac{1}{3} +0\right)&\mbox{}\\ \displaystyle &\displaystyle= \frac{\pi}{3} - \frac{1}{3} +\frac{\pi}{3}+\frac{1}{3}&\mbox{}\\ \displaystyle &\displaystyle=\frac{2\pi}{3} &\mbox{}\\ \end{array} $$
We let $C$ be the cone and $P$ be the plane which make up our piecewise-smooth, closed surface $S$.
Thus $S$ can be expressed as $C \cup P.$
Now, for the closed surface to be positively (outwardly) oriented, the normal vector on the cone must point outward.

That is, we must orient the surface $C$ negatively.
The above leads us to $$ \begin{array}{lll} \displaystyle \iint_S {\bf F}\cdot\, d{\bf S}&\displaystyle=\iint_{C \cup P} {\bf F}\cdot\, d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle=\iint_{C} {\bf F}\cdot\, d{\bf S}+\iint_P {\bf F}\cdot\, d{\bf S} &\mbox{}\\ \displaystyle &\displaystyle= -\left(\iint_D -Pg_x-Q g_y+R \, dA\right)+\iint_D -Ph_x-Q h_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D Pg_x+Q g_y-R \, dA+\iint_D -Ph_x-Q h_y+R \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + z)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(z-y) \, dA+\iint_D -(x-y)\cdot 0-(x+z)\cdot 0+(z-y) \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + z)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(z-y) \, dA+\iint_D z-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+(x + \color{magenta}{g(x,y)})\left(\frac{y}{\sqrt{x^2+y^2}}\right) -(\color{magenta}{g(x,y)}-y) \, dA+\iint_D \color{magenta}{h(x,y)}-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+\left(x + \color{magenta}{\sqrt{x^2+y^2}}\right)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -\left(\color{magenta}{\sqrt{x^2+y^2}}-y\right) \, dA+\iint_D \color{magenta}{1}-y \, dA&\mbox{}\\ %\displaystyle &\displaystyle= \iint_D (x - y)\left(\frac{x}{\sqrt{x^2+y^2}}\right)+\left(x + \sqrt{x^2+y^2}\right)\left(\frac{y}{\sqrt{x^2+y^2}}\right) -\left(1-y\right) \, dA+\iint_D \sqrt{x^2+y^2}-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}}-\frac{xy}{\sqrt{x^2+y^2}}+\frac{xy}{\sqrt{x^2+y^2}}+y -\sqrt{x^2+y^2}+y \, dA+\iint_D 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+2y \, dA+\iint_D 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+2y + 1-y \, dA&\mbox{}\\ \displaystyle &\displaystyle= \iint_D \frac{x^2}{\sqrt{x^2+y^2}} -\sqrt{x^2+y^2}+y + 1 \, dA&\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\int_{0}^{1} \left(\frac{r^2\cos^2 \theta}{r}-r +r\sin \theta +1\right) \, r \, dr \, d\theta &\mbox{convert to polar coordinates}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\int_{0}^{1} r^2\cos^2 \theta-r^2 + r^2\sin \theta +r \, dr \, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\left[\frac{1}{3}r^3\cos^2 \theta-\frac{1}{3}r^3 + \frac{1}{3}r^3\sin \theta +\frac{1}{2}r^2\right]_{0}^{1}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\frac{1}{3}\cos^2 \theta-\frac{1}{3} + \frac{1}{3}\sin \theta +\frac{1}{2}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \int_{0}^{2\pi}\frac{1}{3}\cos^2 \theta + \frac{1}{3}\sin \theta +\frac{1}{6}\, d\theta &\mbox{}\\ \displaystyle &\displaystyle= \left[\frac{1}{3}\left(\frac{1}{2}\theta+\frac{1}{4}\sin(2\theta)\right) - \frac{1}{3}\cos \theta +\frac{1}{6}\theta\right]_{0}^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= \left[\left(\frac{1}{6}\theta+\frac{1}{12}\sin(2\theta)\right) - \frac{1}{3}\cos \theta +\frac{1}{6}\theta\right]_{0}^{2\pi}&\mbox{}\\ \displaystyle &\displaystyle= \left(\frac{1}{6}(2\pi)+\frac{1}{12}\sin(4\pi)\right) - \frac{1}{3}\cos(2\pi) +\frac{1}{6}(2\pi)-\left(\left(\frac{1}{6}(0)+\frac{1}{12}\sin(0)\right) - \frac{1}{3}\cos 0 +\frac{1}{6}(0)\right)&\mbox{}\\ \displaystyle &\displaystyle= \left(\frac{\pi}{3}+0\right) - \frac{1}{3} +\frac{\pi}{3}-\left(0 - \frac{1}{3} +0\right)&\mbox{}\\ \displaystyle &\displaystyle= \frac{\pi}{3} - \frac{1}{3} +\frac{\pi}{3}+\frac{1}{3}&\mbox{}\\ \displaystyle &\displaystyle=\frac{2\pi}{3} &\mbox{}\\ \end{array} $$
Summary of Formulas
$$ \begin{array}{rll} \mbox{Surface Area Parameterized Surface}&&\displaystyle \iint_S \, dS=\iint_D \left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA\\ \mbox{Surface Integral over Parameterized Surface}&&\displaystyle \iint_S f(x,y,z)\, dS=\iint_D f({\bf r}(s,t))\left \Vert {\bf r}_s \times {\bf r}_t \right\Vert \, dA\\ \mbox{Surface Integral over Surface given by $z=g(x,y)$}&&\displaystyle \iint_S f(x,y,z)\, dS=\iint_D f({\bf r}(x,y))\sqrt{g_x^2+g_y^2+1}\, dA\\ \mbox{Normal Vector on Parameterized Surface}&&\displaystyle {\bf N}=\frac{{\bf r}_s \times {\bf r}_t}{\left \Vert {\bf r}_s \times {\bf r}_t \right\Vert} \mbox{ ($S$ positively oriented)}\\ \mbox{Flux Integral over Parameterized Surface}&&\displaystyle \iint_S {\bf F}\cdot d{\bf S}= \iint_D {\bf F}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA\\ \mbox{Flux Integral over Surface given by $z=g(x,y)$}&&\displaystyle \iint_S {\bf F}\cdot d{\bf S}= \iint_D -Pg_x-Q g_y+R \, dA\\\\ \end{array} $$
Application
Let ${\bf v}(x, y, z) = \langle x^2 + y^2, z, 4y \rangle$ $\mbox{m/sec}$ represent a velocity field of a fluid with constant density of $\rho= 100$ $\mbox{kg/m}^3.$
Let $S$ be the half-cylinder ${\bf r}(s, t) = \langle \cos s, \sin s, t \rangle,$ $0 \leq s \leq \pi,$ $0 \leq t \leq 2$ oriented outward (positively).
Calculate the mass flux of the fluid across $S.$
First, ${\bf r}_s = \langle -\sin s, \cos s, 0 \rangle$ and ${\bf r}_t = \langle 0, 0, 1 \rangle$ so that
$$
\begin{array}{ll}
{\bf r}_s\times {\bf r}_t&=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \displaystyle -\sin s & \cos s & 0 \\ 0 & 0 & 1\end{array}\right|\\
&=(\cos s-0){\bf i}-(-\sin s-0){\bf j}+(0-0){\bf k}\\
&=\cos s{\bf i}+\sin s{\bf j}+0{\bf k}\\
&=\langle \cos s,\sin s,0\rangle\\
\end{array}
$$
We may now calculate the flux of the fluid through the surface as
$$
\begin{array}{lll}
\displaystyle \iint_S \rho{\bf v}\cdot d{\bf S}&\displaystyle= \iint_D \rho{\bf v}({\bf r}(s,t))\cdot ({\bf r}_s \times {\bf r}_t) \, dA&\mbox{}\\
\displaystyle &\displaystyle=\iint_D 100 \langle x(s,t)^2+y(s,t)^2,z(s,t),4y(s,t) \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\
\displaystyle &\displaystyle=100 \iint_D \langle \cos^2 s+\sin^2 s,t,4\sin s \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\
\displaystyle &\displaystyle=100 \iint_D \langle 1,t,4\sin s \rangle \cdot \langle \cos s,\sin s,0\rangle \, dA &\mbox{}\\
\displaystyle &\displaystyle=100\iint_D \cos s +t\sin s \, dA &\mbox{}\\
\displaystyle &\displaystyle=100\int_{0}^{2}\int_{0}^{\pi} \cos s +t\sin s \, ds \, dt &\mbox{}\\
\displaystyle &\displaystyle=100\int_{0}^{2} \left[\sin s -t\cos s \right]_{0}^{\pi} \, dt &\mbox{}\\
\displaystyle &\displaystyle=100\int_{0}^{2} \sin \pi -t\cos \pi-\left(\sin 0 -t\cos 0 \right) \, dt &\mbox{}\\
\displaystyle &\displaystyle=100\int_{0}^{2} 0 -t(-1)-\left(0 -t \right) \, dt &\mbox{}\\
\displaystyle &\displaystyle=100\int_{0}^{2} 2t \, dt &\mbox{}\\
\displaystyle &\displaystyle=100[t^2]_{0}^{2} &\mbox{}\\
\displaystyle &\displaystyle=100\cdot 4&\mbox{}\\
\displaystyle &\displaystyle=400&\mbox{}\\
\end{array}
$$
Thus the flux is $400$ $\mbox{kg/m$^2$/sec}.$
Heat Flow
Flux integrals are also important in modelling how heat flows through a surface $S.$
Heat flows in a direction opposite of the gradient of temperature $T(x,y,z).$ That is, $$ {\bf F}=-k\nabla T $$ where $k$ is an experimentally-determined constant constant called the thermal conductivity which models how easily heat flows through a particular kind of material.
The rate at which heat flows across a surface $S$ is given by the flux integral $$ \iint_S {\bf F}\cdot d{\bf S}=\iint_S -k\nabla T \cdot d{\bf S} $$
Application
A cast-iron solid ball is given by inequality $x^2 + y^2 + z^2 \leq 1.$
The temperature at a point in this region is $$ T(x, y, z) = \frac{1}{3}(x^2 + y^2 + z^2) $$ Given that the thermal conductivity of cast iron is $k=55,$ find the heat flow across the boundary of the solid if this boundary is oriented outward (positively).
We'll use the standard parameterization of the sphere to describe the boundary of the region.
Again, instead of using $s$ and $t$ as parameters, we shall use $\phi$ and $\theta.$
The sphere of radius $1$ is parameterized as $$ {\bf r}(\phi, \theta) = \langle \cos \theta \sin \phi, \sin \theta \sin \phi, \cos \phi \rangle $$ over $0 \leq \theta \leq 2\pi$ and $0 \leq \phi \leq \pi.$
First we note that ${\bf r}_{\phi}=\langle \cos \theta \cos \phi, \sin \theta \cos \phi, - \sin \phi \rangle$ and ${\bf r}_{\theta}\langle - \sin \theta \sin \phi, \cos \theta \sin \phi, 0 \rangle.$
Now we compute ${\bf r}_{\phi}\times {\bf r}_{\theta}.$ $$ \begin{array}{lll} \displaystyle {\bf r}_{\phi}\times {\bf r}_{\theta}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \cos \theta \cos \phi & \sin \theta \cos \phi & - \sin \phi \\ - \sin \theta \sin \phi & \cos \theta \sin \phi & 0 \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-(-\cos\theta \sin^2 \phi)){\bf i}-(0-\sin \theta \sin^2 \phi){\bf j}+(\cos^2 \theta \cos \phi \sin \phi+\sin^2\theta \cos \phi \sin \phi){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\cos\theta \sin^2 \phi\,{\bf i}+\sin \theta \sin^2 \phi\,{\bf j}+(\cos^2 \theta +\sin^2\theta)\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\cos\theta \sin^2 \phi\,{\bf i}+\sin \theta \sin^2 \phi\,{\bf j}+\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle &\mbox{}\\ \end{array} $$ The heat flux integral through the surface $S$ is then $$ \begin{array}{lll} %\displaystyle \iint_S {\bf F}\cdot d{\bf S}&\displaystyle=\iint_S -k\nabla T \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_S -k\nabla T \cdot d{\bf S}&\displaystyle=\iint_D -k\nabla T \cdot ({\bf r}_{\phi}\times {\bf r}_{\theta}) \,dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D -55\left\langle \frac{\partial T}{\partial x},\frac{\partial T}{\partial y},\frac{\partial T}{\partial z} \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-55\iint_D \left\langle \frac{1}{3}(2x),\frac{1}{3}(2y),\frac{1}{3}(2z) \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-55\cdot \frac{2}{3}\iint_D \left\langle x,y,z \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \left\langle x(\phi,\theta),y(\phi,\theta),z(\phi,\theta) \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \langle \cos \theta \sin \phi, \sin \theta \sin \phi, \cos \phi \rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \cos^2\theta \sin^3\phi +\sin^2\theta\sin^3 \phi +\cos^2 \phi \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin^3 \phi +\cos^2 \phi \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin \phi(\sin^2 \phi +\cos^2 \phi) \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\int_{0}^{2\pi}\int_{0}^{\pi} \sin \phi \,d\phi\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\int_{0}^{2\pi}\,d\theta \int_{0}^{\pi} \sin \phi \,d\phi&\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\cdot 2\pi \left[-\cos \phi \right]_{0}^{\pi}&\mbox{}\\ \displaystyle &\displaystyle=-\frac{220\pi}{3}\cdot \left[-\cos(\pi)+\cos(0) \right]&\mbox{}\\ \displaystyle &\displaystyle=-\frac{220\pi}{3}\cdot 2&\mbox{}\\ \displaystyle &\displaystyle=-\frac{440\pi}{3}&\mbox{}\\ \displaystyle &\displaystyle\approx -460.7669225&\mbox{}\\ \end{array} $$
Again, instead of using $s$ and $t$ as parameters, we shall use $\phi$ and $\theta.$
The sphere of radius $1$ is parameterized as $$ {\bf r}(\phi, \theta) = \langle \cos \theta \sin \phi, \sin \theta \sin \phi, \cos \phi \rangle $$ over $0 \leq \theta \leq 2\pi$ and $0 \leq \phi \leq \pi.$
First we note that ${\bf r}_{\phi}=\langle \cos \theta \cos \phi, \sin \theta \cos \phi, - \sin \phi \rangle$ and ${\bf r}_{\theta}\langle - \sin \theta \sin \phi, \cos \theta \sin \phi, 0 \rangle.$
Now we compute ${\bf r}_{\phi}\times {\bf r}_{\theta}.$ $$ \begin{array}{lll} \displaystyle {\bf r}_{\phi}\times {\bf r}_{\theta}&\displaystyle=\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\ \cos \theta \cos \phi & \sin \theta \cos \phi & - \sin \phi \\ - \sin \theta \sin \phi & \cos \theta \sin \phi & 0 \end{array}\right| &\mbox{}\\ \displaystyle &\displaystyle=(0-(-\cos\theta \sin^2 \phi)){\bf i}-(0-\sin \theta \sin^2 \phi){\bf j}+(\cos^2 \theta \cos \phi \sin \phi+\sin^2\theta \cos \phi \sin \phi){\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\cos\theta \sin^2 \phi\,{\bf i}+\sin \theta \sin^2 \phi\,{\bf j}+(\cos^2 \theta +\sin^2\theta)\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\cos\theta \sin^2 \phi\,{\bf i}+\sin \theta \sin^2 \phi\,{\bf j}+\cos \phi \sin \phi\,{\bf k} &\mbox{}\\ \displaystyle &\displaystyle=\langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle &\mbox{}\\ \end{array} $$ The heat flux integral through the surface $S$ is then $$ \begin{array}{lll} %\displaystyle \iint_S {\bf F}\cdot d{\bf S}&\displaystyle=\iint_S -k\nabla T \cdot d{\bf S} &\mbox{}\\ \displaystyle \iint_S -k\nabla T \cdot d{\bf S}&\displaystyle=\iint_D -k\nabla T \cdot ({\bf r}_{\phi}\times {\bf r}_{\theta}) \,dA &\mbox{}\\ \displaystyle &\displaystyle=\iint_D -55\left\langle \frac{\partial T}{\partial x},\frac{\partial T}{\partial y},\frac{\partial T}{\partial z} \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-55\iint_D \left\langle \frac{1}{3}(2x),\frac{1}{3}(2y),\frac{1}{3}(2z) \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-55\cdot \frac{2}{3}\iint_D \left\langle x,y,z \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \left\langle x(\phi,\theta),y(\phi,\theta),z(\phi,\theta) \right\rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \langle \cos \theta \sin \phi, \sin \theta \sin \phi, \cos \phi \rangle \cdot \langle \cos\theta \sin^2 \phi,\sin \theta \sin^2 \phi,\cos \phi \sin \phi\rangle \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \cos^2\theta \sin^3\phi +\sin^2\theta\sin^3 \phi +\cos^2 \phi \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin^3 \phi +\cos^2 \phi \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin \phi(\sin^2 \phi +\cos^2 \phi) \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\iint_D \sin \phi \,dA &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\int_{0}^{2\pi}\int_{0}^{\pi} \sin \phi \,d\phi\,d\theta &\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\int_{0}^{2\pi}\,d\theta \int_{0}^{\pi} \sin \phi \,d\phi&\mbox{}\\ \displaystyle &\displaystyle=-\frac{110}{3}\cdot 2\pi \left[-\cos \phi \right]_{0}^{\pi}&\mbox{}\\ \displaystyle &\displaystyle=-\frac{220\pi}{3}\cdot \left[-\cos(\pi)+\cos(0) \right]&\mbox{}\\ \displaystyle &\displaystyle=-\frac{220\pi}{3}\cdot 2&\mbox{}\\ \displaystyle &\displaystyle=-\frac{440\pi}{3}&\mbox{}\\ \displaystyle &\displaystyle\approx -460.7669225&\mbox{}\\ \end{array} $$