We will now learn how to deal with areas, lengths, and slopes of tangent lines in the polar setting.
The Area of a Polar Curve
We begin by partitioning up the the angle swept out by a curve into subintervals.
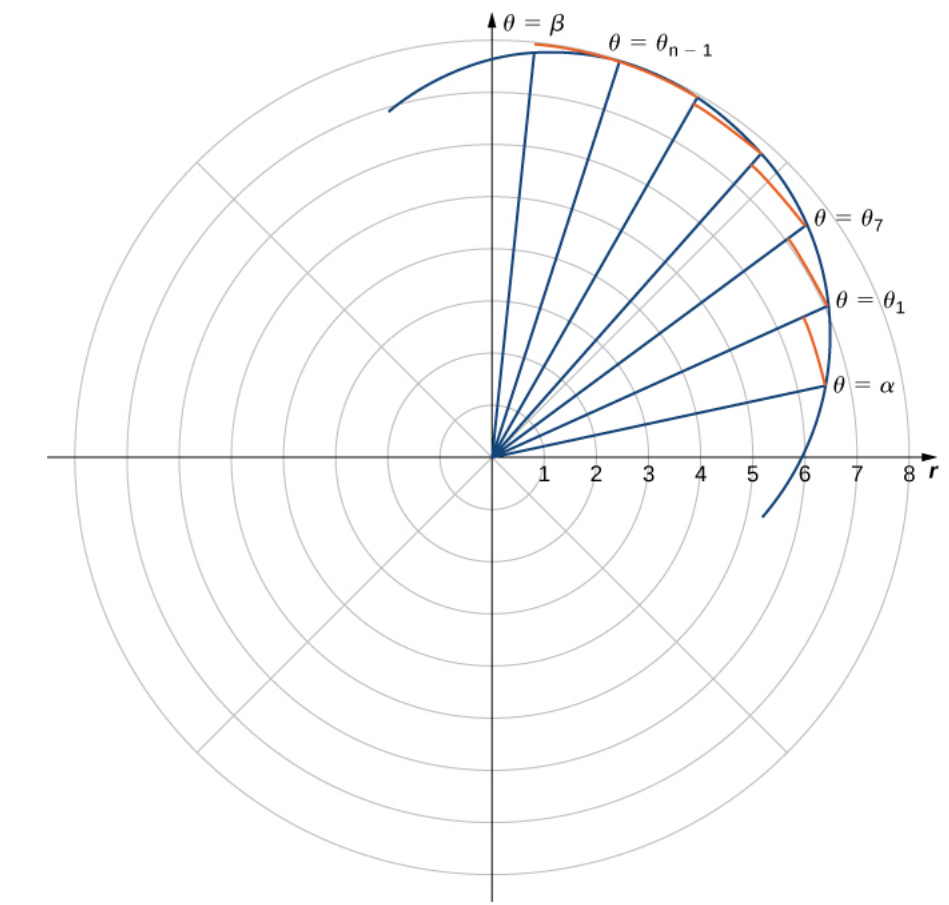
Although the above picture looks different that for curves in rectangular coordinates, the expression for the approximating area really is a Riemann sum. Each sector is the circular equivalent of a rectangle.
The area of a sector of a circle of radius $r$ subtending an angle $\theta$ is given by
$$
\frac{\theta}{2\pi}\cdot \pi r^2=\frac{1}{2}r^2 \theta
$$
Then the area of the sectors approximating the area in the figure is given by
$$
\mbox{Area}\approx\sum_{j=0}^{n-1}\frac{1}{2} r_i^2 \Delta \theta
=\sum_{j=0}^{n-1}\frac{1}{2} f(\theta_i)^2 \Delta \theta
$$
In the limit we have
$$
\mbox{Area}=\lim_{n \rightarrow \infty} \sum_{j=0}^{n-1}\frac{1}{2} f(\theta_i)^2 \Delta \theta=\int_{\alpha}^{\beta}\frac{1}{2} f(\theta)^2 \,d\theta
$$
The Area of a Polar Curve
Suppose $f$ is continuous and nonnegative on the interval $\alpha ≤ \theta ≤ \beta$ with $0 \lt \beta − \alpha ≤ 2\pi.$ The area of the region bounded by the graph of $r = f (\theta)$ between the radial lines $\theta = \alpha$ and $\theta = \beta$ is $$\frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta.$$
The Area of a Polar Curve
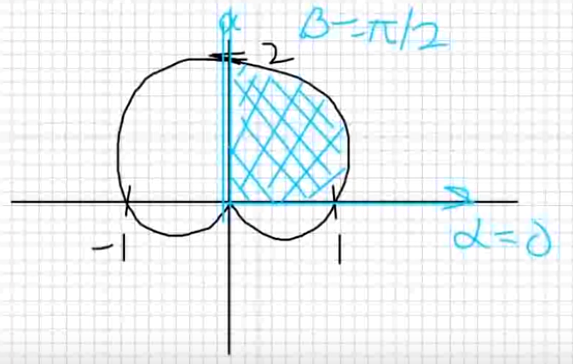
Example: Determine and evaluate a definite integral that represents the area of the region in the first quadrant within the cardioid $r=1+\sin \theta.$
We we want to find the area of the cardioid in the first quadrant. This means $\displaystyle 0\leq \theta \leq \frac{\pi}{2}.$
We now sketch the region.
 $$
\begin{array}{lll}
\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} [1+\sin \theta]^2 \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} 1+2\sin \theta +\sin^2\theta\, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} 1+2\sin \theta +\frac{1-\cos(2\theta)}{2}\, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[ \theta-2\cos \theta +\frac{\theta}{2}-\frac{\sin(2\theta)}{4}\right]_{0}^{\pi/2}&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\left(\frac{\pi}{2}-2\cos \frac{\pi}{2} +\frac{\frac{\pi}{2}}{2} -\frac{\sin\left(2\cdot\frac{\pi}{2}\right)}{4}\right)- \left(0-2\cos 0 +\frac{0}{2} -\frac{\sin(2\cdot 0)}{4}\right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\left(\frac{\pi}{2} +\frac{\pi}{4}\right)- \left(-2\right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\frac{3\pi}{4} +2\right]&\mbox{}\\
&=\displaystyle \frac{3\pi}{8} +1&\mbox{}\\
&\approx \displaystyle 2.178097245&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} [1+\sin \theta]^2 \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} 1+2\sin \theta +\sin^2\theta\, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{0}^{\pi/2} 1+2\sin \theta +\frac{1-\cos(2\theta)}{2}\, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[ \theta-2\cos \theta +\frac{\theta}{2}-\frac{\sin(2\theta)}{4}\right]_{0}^{\pi/2}&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\left(\frac{\pi}{2}-2\cos \frac{\pi}{2} +\frac{\frac{\pi}{2}}{2} -\frac{\sin\left(2\cdot\frac{\pi}{2}\right)}{4}\right)- \left(0-2\cos 0 +\frac{0}{2} -\frac{\sin(2\cdot 0)}{4}\right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\left(\frac{\pi}{2} +\frac{\pi}{4}\right)- \left(-2\right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{2}\left[\frac{3\pi}{4} +2\right]&\mbox{}\\
&=\displaystyle \frac{3\pi}{8} +1&\mbox{}\\
&\approx \displaystyle 2.178097245&\mbox{}\\
\end{array}
$$
We now sketch the region.

Example: Determine and evaluate a definite integral that represents the area of the region enclosed by one petal of $r = \cos(3\theta).$
We want to find the area of a single petal. This means $\displaystyle -\frac{\pi}{6}\leq \theta \leq \frac{\pi}{6}.$
Using a few points, we know that at $0$ radians $r=1,$ and since $\cos x$ is $0$ when $x=\frac{\pi}{2},$ we know that at $\theta=\frac{\pi}{6},$ $r=0.$ This is makes the upper half of the petal.
Also, since $\cos x$ is even, $f(-\theta)=\cos(3(-\theta))=\cos(3\theta)=f(\theta).$ That is, the curve is symmetrical about the horizontal axis.
We now sketch the region.
 $$
\begin{array}{lll}
\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} [\cos(3\theta)]^2 \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} \cos^2(3\theta) \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} \frac{1+\cos(6\theta)}{2} \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{4}\int_{-\pi/6}^{\pi/6} 1+\cos(6\theta) \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \theta+\frac{1}{6}\sin(6\theta) \right]_{-\pi/6}^{\pi/6}&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \frac{\pi}{6}+\frac{1}{6}\sin\left(6\cdot \frac{\pi}{6}\right) -\left(-\frac{\pi}{6}+\frac{1}{6}\sin\left(6\cdot \left(-\frac{\pi}{6}\right)\right) \right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \frac{\pi}{6}+\frac{\pi}{6}\right]&\mbox{}\\
&=\displaystyle \frac{\pi}{12}&\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} [\cos(3\theta)]^2 \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} \cos^2(3\theta) \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{-\pi/6}^{\pi/6} \frac{1+\cos(6\theta)}{2} \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{4}\int_{-\pi/6}^{\pi/6} 1+\cos(6\theta) \, d\theta&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \theta+\frac{1}{6}\sin(6\theta) \right]_{-\pi/6}^{\pi/6}&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \frac{\pi}{6}+\frac{1}{6}\sin\left(6\cdot \frac{\pi}{6}\right) -\left(-\frac{\pi}{6}+\frac{1}{6}\sin\left(6\cdot \left(-\frac{\pi}{6}\right)\right) \right)\right]&\mbox{}\\
&=\displaystyle \frac{1}{4}\left[ \frac{\pi}{6}+\frac{\pi}{6}\right]&\mbox{}\\
&=\displaystyle \frac{\pi}{12}&\mbox{}\\
\end{array}
$$
Using a few points, we know that at $0$ radians $r=1,$ and since $\cos x$ is $0$ when $x=\frac{\pi}{2},$ we know that at $\theta=\frac{\pi}{6},$ $r=0.$ This is makes the upper half of the petal.
Also, since $\cos x$ is even, $f(-\theta)=\cos(3(-\theta))=\cos(3\theta)=f(\theta).$ That is, the curve is symmetrical about the horizontal axis.
We now sketch the region.

The Area Between Polar Curves
Example: Find the area outside the cardioid $r = 2 + 2 \sin \theta$ and inside the circle $r = 6 \sin \theta.$

Letting $f(\theta)=6\sin \theta$ and $g(\theta)=2+2\sin \theta,$ we find the angles where the curves intersect by solving the equation
$f(\theta)=g(\theta),$ or
$$
6\sin \theta=2+2\sin \theta
$$
Then
$$
\begin{array}{lll}
&\displaystyle 4\sin \theta=2 &\mbox{}\\
\implies &\displaystyle \sin \theta =\frac{1}{2}&\mbox{}\\
\implies &\displaystyle \theta =\frac{\pi}{6} \mbox{ or } \theta=\frac{5\pi}{6}&\mbox{}\\
\end{array}
$$
Summarizing the above in in a figure,
 The area between curves is then
$$
\begin{array}{lll}
\displaystyle \mbox{Outer Area}-\mbox{Inner Area}
&=\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta-\frac{1}{2}\int_{\alpha}^{\beta} [g(\theta)]^2 \, d \theta\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} [6\sin \theta]^2 \, d \theta - \frac{1}{2}\int_{\pi/6}^{5\pi/6} [2+2\sin \theta)]^2 \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta \, d \theta - \frac{1}{2}\int_{\pi/6}^{5\pi/6} 4+8\sin \theta +4\sin^2 \theta \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta - (4+8\sin \theta +4\sin^2 \theta) \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta - 4-8\sin \theta -4\sin^2 \theta \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 32\sin^2 \theta -8\sin \theta -4\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 16\sin^2 \theta -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 16\frac{1-\cos(2\theta)}{2} -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 8(1-\cos(2\theta)) -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 8-8\cos(2\theta) -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 6-8\cos(2\theta) -4\sin \theta \, d \theta&\mbox{}\\
&=\displaystyle \left[ 6\theta-4\sin(2\theta) +4\cos \theta \right]_{\pi/6}^{5\pi/6}&\mbox{}\\
&=\displaystyle \left[ 6\cdot\frac{5\pi}{6}-4\sin\left(2\cdot \frac{5\pi}{6}\right) +4\cos \frac{5\pi}{6} \right]-\left[6\cdot\frac{\pi}{6}-4\sin\left(2\cdot\frac{\pi}{6}\right) +4\cos \frac{\pi}{6} \right]&\mbox{}\\
&=\displaystyle 5\pi-4\sin\left(\frac{5\pi}{3}\right) +4\cos \frac{5\pi}{6}-\frac{\pi}{6}+4\sin\left(\frac{\pi}{3}\right) -4\cos \frac{\pi}{6}&\mbox{}\\
&=\displaystyle 5\pi-4\sin\left(\frac{5\pi}{3}\right) +4\cos \frac{5\pi}{6}-\pi+4\sin\left(\frac{\pi}{3}\right) -4\cos \frac{\pi}{6}&\mbox{}\\
&=\displaystyle 4\pi-4\left(-\frac{\sqrt{3}}{2}\right) +4\left(-\frac{\sqrt{3}}{2}\right)+4\left(\frac{\sqrt{3}}{2}\right) -4\left(\frac{\sqrt{3}}{2}\right)&\mbox{}\\
&=\displaystyle 4\pi+2\sqrt{3} -2\sqrt{3}+2\sqrt{3} -2\sqrt{3}&\mbox{}\\
&=\displaystyle 4\pi&\mbox{}\\
&\approx \displaystyle 12.566370614 &\mbox{}\\
\end{array}
$$
The area between curves is then
$$
\begin{array}{lll}
\displaystyle \mbox{Outer Area}-\mbox{Inner Area}
&=\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta-\frac{1}{2}\int_{\alpha}^{\beta} [g(\theta)]^2 \, d \theta\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} [6\sin \theta]^2 \, d \theta - \frac{1}{2}\int_{\pi/6}^{5\pi/6} [2+2\sin \theta)]^2 \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta \, d \theta - \frac{1}{2}\int_{\pi/6}^{5\pi/6} 4+8\sin \theta +4\sin^2 \theta \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta - (4+8\sin \theta +4\sin^2 \theta) \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 36\sin^2 \theta - 4-8\sin \theta -4\sin^2 \theta \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{\pi/6}^{5\pi/6} 32\sin^2 \theta -8\sin \theta -4\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 16\sin^2 \theta -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 16\frac{1-\cos(2\theta)}{2} -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 8(1-\cos(2\theta)) -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 8-8\cos(2\theta) -4\sin \theta -2\, d \theta&\mbox{}\\
&=\displaystyle \int_{\pi/6}^{5\pi/6} 6-8\cos(2\theta) -4\sin \theta \, d \theta&\mbox{}\\
&=\displaystyle \left[ 6\theta-4\sin(2\theta) +4\cos \theta \right]_{\pi/6}^{5\pi/6}&\mbox{}\\
&=\displaystyle \left[ 6\cdot\frac{5\pi}{6}-4\sin\left(2\cdot \frac{5\pi}{6}\right) +4\cos \frac{5\pi}{6} \right]-\left[6\cdot\frac{\pi}{6}-4\sin\left(2\cdot\frac{\pi}{6}\right) +4\cos \frac{\pi}{6} \right]&\mbox{}\\
&=\displaystyle 5\pi-4\sin\left(\frac{5\pi}{3}\right) +4\cos \frac{5\pi}{6}-\frac{\pi}{6}+4\sin\left(\frac{\pi}{3}\right) -4\cos \frac{\pi}{6}&\mbox{}\\
&=\displaystyle 5\pi-4\sin\left(\frac{5\pi}{3}\right) +4\cos \frac{5\pi}{6}-\pi+4\sin\left(\frac{\pi}{3}\right) -4\cos \frac{\pi}{6}&\mbox{}\\
&=\displaystyle 4\pi-4\left(-\frac{\sqrt{3}}{2}\right) +4\left(-\frac{\sqrt{3}}{2}\right)+4\left(\frac{\sqrt{3}}{2}\right) -4\left(\frac{\sqrt{3}}{2}\right)&\mbox{}\\
&=\displaystyle 4\pi+2\sqrt{3} -2\sqrt{3}+2\sqrt{3} -2\sqrt{3}&\mbox{}\\
&=\displaystyle 4\pi&\mbox{}\\
&\approx \displaystyle 12.566370614 &\mbox{}\\
\end{array}
$$

The Area of a Polar Curve
Application: A microphone whose directionality is modelled by the polar curve $r=10+10\sin \theta$ (with $r$ measured in feet) is placed at the front of a stage where a vocal group will be performing. Beyond this polar curve, the mic won't properly record.
What is the area of region the performers can sing and still get a good recording while performing?
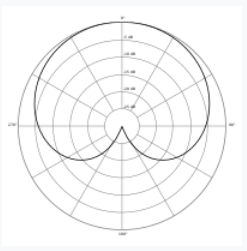
Since the region is modelled by $r=10+10\sin \theta,$ the area we're interested in is given by
$$
\begin{array}{lll}
\displaystyle \frac{1}{2}\int_{\alpha}^{\beta} [f(\theta)]^2 \, d \theta
&=\displaystyle \frac{1}{2}\int_{0}^{2\pi} [10+10\sin \theta]^2 \, d \theta&\mbox{}\\
&=\displaystyle \frac{1}{2}\int_{0}^{2\pi} 100[1+\sin \theta]^2 \, d \theta&\mbox{}\\
&=\displaystyle 50\int_{0}^{2\pi} 1+2\sin \theta +\sin^2\theta\, d \theta&\mbox{}\\
&=\displaystyle 50\int_{0}^{2\pi} 1+2\sin \theta +\frac{1-\cos(2\theta)}{2}\, d \theta&\mbox{}\\
&=\displaystyle 50\left[ \theta-2\cos \theta +\frac{\theta}{2}-\frac{\sin(2\theta)}{4}\right]_{0}^{2\pi}&\mbox{}\\
&=\displaystyle 50\left[\left(2\pi-2\cos (2\pi) +\frac{2\pi}{2} -\frac{\sin(2\pi)}{4}\right)- \left(0-2\cos 0 +\frac{0}{2} -\frac{\sin(2\cdot 0)}{4}\right)\right]&\mbox{}\\
&=\displaystyle 50\left[\left(2\pi-2 +\pi \right)- \left(-2 \right)\right]&\mbox{}\\
&=\displaystyle 50\left[3\pi\right]&\mbox{}\\
&\approx \displaystyle 471.238898038&\mbox{}\\
\end{array}
$$
That is, the performers have about $471$ square feet of space to freely move and still get a good recording.
The Arc Length of a Polar Curve
Let $f$ be a function whose derivative is continuous on an interval $\alpha ≤ \theta ≤ \beta.$ The length of the graph of $r = f (\theta)$ from $\theta = \alpha$ to $\theta = \beta$ is $$\int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta.$$
The Arc Length of a Polar Curve
Example: Find the length of the curve $r = e^{3\theta}$ on the interval $\displaystyle 0 \leq \theta \leq 2.$
The length of the curve is given by
$$
\begin{array}{lll}
\displaystyle \int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta
&=\displaystyle \int_{0}^{2} \sqrt{[e^{3\theta}]^2+[3e^{3\theta}]^2} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2} \sqrt{e^{6\theta}+9e^{6\theta}} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2} \sqrt{10e^{6\theta}} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2} \sqrt{10}\sqrt{e^{6\theta}} \, d \theta&\mbox{}\\
&=\displaystyle \sqrt{10}\int_{0}^{2} e^{3\theta} \, d \theta&\mbox{}\\
&=\displaystyle \sqrt{10}\left[ \frac{1}{3}e^{3\theta}\right]_{0}^{2}&\mbox{}\\
&=\displaystyle \sqrt{10}\left[ \frac{1}{3}e^{6}-\frac{1}{3}\right]&\mbox{}\\
&=\displaystyle \frac{\sqrt{10}}{3}\left[e^{6}-1\right]&\mbox{}\\
&\approx\displaystyle 424.1971945&\mbox{}\\
\end{array}
$$
The length of the curve is about $424.2$ units.
Example: Find and evaluate a definite integral that represents the arc length of $r = 1+ \sin \theta$ on the interval $\displaystyle 0 \leq \theta \leq 2\pi.$
The length of the curve is given by
$$
\begin{array}{lll}
\displaystyle \int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta
&=\displaystyle \int_{0}^{2\pi} \sqrt{[1+ \sin \theta]^2+[\cos \theta]^2} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{1+ 2\sin \theta+\sin^2 \theta+\cos^2 \theta} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{1+ 2\sin \theta+1} \, d \theta&\mbox{Pythagorean Identity!}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{2+ 2\sin \theta} \, d \theta&\mbox{}\\
\end{array}
$$
We now need to do some shenanigans. We recall the identity $\displaystyle \cos^2 x=\frac{1+\cos(2x)}{2}$ and rewrite it as
$$
\cos^2 \left(\frac{x}{2}\right)=\frac{1+\cos(x)}{2}
$$
Then, multiplying the above by $4$ we have
$$
4\cos^2\left(\frac{x}{2}\right)=2+2\cos(x)
$$
We may now proceed with our arc-length calculation.
$$
\begin{array}{lll}
\displaystyle \int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta
&=\displaystyle \int_{0}^{2\pi} \sqrt{2+ 2\sin \theta} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{2+ 2\cos\left(\frac{\pi}{2}- \theta\right)} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{4\cos^2\left(\frac{\frac{\pi}{2}- \theta}{2}\right)} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} \sqrt{4\cos^2\left(\frac{\pi}{4}- \frac{\theta}{2}\right)} \, d \theta&\mbox{}\\
&=\displaystyle \int_{0}^{2\pi} 2\left|\cos\left(\frac{\pi}{4}- \frac{\theta}{2}\right)\right| \, d \theta&\mbox{}\\
&=\displaystyle 2\int_{0}^{2\pi} \left|\cos\left(\frac{\pi}{4}- \frac{\theta}{2}\right)\right| \, d \theta&\mbox{}\\
&=\displaystyle 2\int_{0}^{2\pi} \left|\cos\left(\frac{\pi}{4}- \frac{\theta}{2}\right)\right| \, d \theta&\mbox{}\\
\end{array}
$$
We now perform a $u$ substitution. Let $\displaystyle u=\frac{\pi}{4}- \frac{\theta}{2}$ so that $\displaystyle -2\,du=d\theta.$
The lower limit of integration is $u=\frac{\pi}{4},$ and the upper limit is $u=-\frac{3\pi}{4}.$ Continuing the above calculation, $$ \begin{array}{lll} \displaystyle \int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta &=\displaystyle 2\int_{0}^{2\pi} \left|\cos\left(\frac{\pi}{4}- \frac{\theta}{2}\right)\right| \, d \theta&\mbox{}\\ &=\displaystyle 2\int_{\pi/4}^{-3\pi/4} \left|\cos\left(u\right)\right| (-2\, du)&\mbox{}\\ &=\displaystyle -4\int_{\pi/4}^{-3\pi/4} \left|\cos\left(u\right)\right| \, du&\mbox{}\\ &=\displaystyle 4\int_{-3\pi/4}^{\pi/4} \left|\cos\left(u\right)\right| \, du&\mbox{}\\ &=\displaystyle 4\left(\left|\int_{-3\pi/4}^{-\pi/2} \cos\left(u\right) \, du\right|+\int_{-\pi/2}^{\pi/4} \cos\left(u\right) \, du\right)&\mbox{see figure below}\\ &=\displaystyle 4\left(\left|\left[\sin\left(u\right)\right]_{-3\pi/4}^{-\pi/2}\right|+\left[ \sin\left(u\right) \right]_{-\pi/2}^{\pi/4}\right)&\mbox{}\\ &=\displaystyle 4\left(\left|\sin\left(-\frac{\pi}{2}\right)-\sin\left(-\frac{3\pi}{4}\right)\right|+\left[\sin\left(\frac{\pi}{4}\right) - \sin\left(-\frac{\pi}{2}\right) \right]\right)&\mbox{}\\ &=\displaystyle 4\left(\left|-1-\left(-\frac{\sqrt{2}}{2}\right)\right|+\left[\frac{\sqrt{2}}{2} - \left(-1\right) \right]\right)&\mbox{}\\ &=\displaystyle 4\left(\left|-1+\frac{\sqrt{2}}{2}\right|+\frac{\sqrt{2}}{2}+1\right)&\mbox{}\\ &=\displaystyle 4\left(1-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}+1\right)&\mbox{}\\ &=\displaystyle 4\left(2\right)&\mbox{}\\ &=\displaystyle 8&\mbox{}\\ \end{array} $$ Thus, the length of the polar curve $r = 1+ \sin \theta$ on the interval $\displaystyle 0 \leq \theta \leq 2\pi$ is $8.$
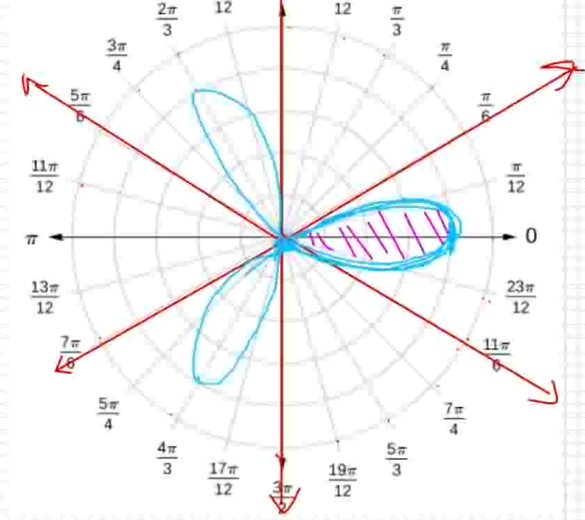
For the above integral, $\displaystyle \int_{-3\pi/4}^{\pi/4} \left|\cos\left(u\right)\right| \, du,$ it helps to keep the graph of $y=|\cos(u)|$ in mind.
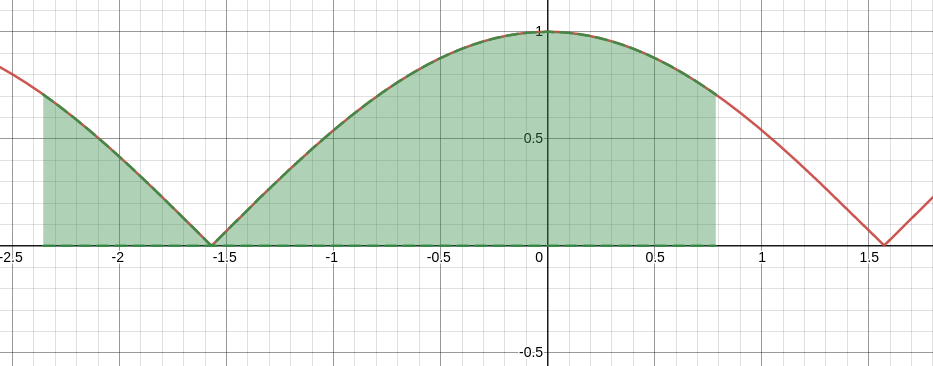
The lower limit of integration is $u=\frac{\pi}{4},$ and the upper limit is $u=-\frac{3\pi}{4}.$ Continuing the above calculation, $$ \begin{array}{lll} \displaystyle \int_{\alpha}^{\beta} \sqrt{[f(\theta)]^2+[f'(\theta)]^2} \, d \theta &=\displaystyle 2\int_{0}^{2\pi} \left|\cos\left(\frac{\pi}{4}- \frac{\theta}{2}\right)\right| \, d \theta&\mbox{}\\ &=\displaystyle 2\int_{\pi/4}^{-3\pi/4} \left|\cos\left(u\right)\right| (-2\, du)&\mbox{}\\ &=\displaystyle -4\int_{\pi/4}^{-3\pi/4} \left|\cos\left(u\right)\right| \, du&\mbox{}\\ &=\displaystyle 4\int_{-3\pi/4}^{\pi/4} \left|\cos\left(u\right)\right| \, du&\mbox{}\\ &=\displaystyle 4\left(\left|\int_{-3\pi/4}^{-\pi/2} \cos\left(u\right) \, du\right|+\int_{-\pi/2}^{\pi/4} \cos\left(u\right) \, du\right)&\mbox{see figure below}\\ &=\displaystyle 4\left(\left|\left[\sin\left(u\right)\right]_{-3\pi/4}^{-\pi/2}\right|+\left[ \sin\left(u\right) \right]_{-\pi/2}^{\pi/4}\right)&\mbox{}\\ &=\displaystyle 4\left(\left|\sin\left(-\frac{\pi}{2}\right)-\sin\left(-\frac{3\pi}{4}\right)\right|+\left[\sin\left(\frac{\pi}{4}\right) - \sin\left(-\frac{\pi}{2}\right) \right]\right)&\mbox{}\\ &=\displaystyle 4\left(\left|-1-\left(-\frac{\sqrt{2}}{2}\right)\right|+\left[\frac{\sqrt{2}}{2} - \left(-1\right) \right]\right)&\mbox{}\\ &=\displaystyle 4\left(\left|-1+\frac{\sqrt{2}}{2}\right|+\frac{\sqrt{2}}{2}+1\right)&\mbox{}\\ &=\displaystyle 4\left(1-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}+1\right)&\mbox{}\\ &=\displaystyle 4\left(2\right)&\mbox{}\\ &=\displaystyle 8&\mbox{}\\ \end{array} $$ Thus, the length of the polar curve $r = 1+ \sin \theta$ on the interval $\displaystyle 0 \leq \theta \leq 2\pi$ is $8.$
For the above integral, $\displaystyle \int_{-3\pi/4}^{\pi/4} \left|\cos\left(u\right)\right| \, du,$ it helps to keep the graph of $y=|\cos(u)|$ in mind.

Slopes of Tangent Lines of Polar Curves: For the curve $r=3(1+\cos \theta)$ at the point $\displaystyle \left(3+3\frac{\sqrt{2}}{2},\frac{5\pi}{4}\right),$ find the slope of a tangent line.
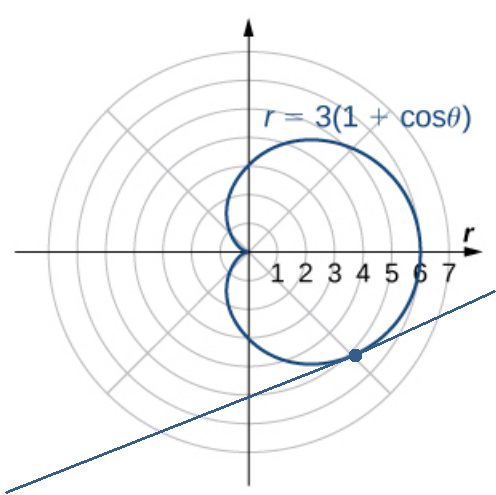
Big Hint: For a general polar curve $r = f (\theta),$ let $x = r \cos \theta = f (\theta)\cos \theta$ and $y = r \sin \theta = f (\theta)\sin \theta,$ so the polar equation $r = f (\theta)$ is now written in parametric form where $\theta$ is the parameter. Then use $\displaystyle \frac{dy}{dx}=\frac{dy/d\theta}{dx/d\theta}$ to find the slope.
We write the parametric representation of $r=3(1+\cos \theta)$ as
$$
\begin{array}{l}
x=3(1+\cos \theta)\cos \theta\\
y=3(1+\cos \theta)\sin \theta
\end{array}
$$
Then
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}
&=\displaystyle \frac{y'(\theta)}{x'(\theta)}&\mbox{}\\
&=\displaystyle \frac{[3(1+\cos \theta)\sin \theta]'}{[3(1+\cos \theta)\cos \theta]'}&\mbox{}\\
&=\displaystyle \frac{[(1+\cos \theta)\sin \theta]'}{[(1+\cos \theta)\cos \theta]'}&\mbox{}\\
&=\displaystyle \frac{(1+\cos \theta)'(\sin \theta)+(1+\cos \theta)(\sin \theta)'}{(1+\cos \theta)'(\cos \theta)+(1+\cos \theta)(\cos \theta)'}&\mbox{}\\
&=\displaystyle \frac{-\sin \theta \sin \theta +(1+\cos \theta)\cos \theta}{-\sin \theta \cos \theta+(1+\cos \theta)(-\sin \theta)}&\mbox{}\\
&=\displaystyle \frac{-\sin^2 \theta +\cos \theta+\cos^2 \theta}{-\sin \theta \cos \theta-\sin \theta-\sin \theta \cos \theta}&\mbox{}\\
&=\displaystyle \frac{\cos \theta-\sin^2 \theta +\cos^2 \theta}{-\sin \theta-2\sin \theta \cos \theta}&\mbox{}\\
\end{array}
$$
From the figure, we see that the point $\displaystyle \left(3+3\frac{\sqrt{2}}{2},\frac{5\pi}{4}\right)$ corresponds to the angle
$\displaystyle \theta=-\frac{\pi}{4}.$ Then
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}\Bigr|_{\theta=-\frac{\pi}{4}}
&=\displaystyle \frac{y'\left(-\frac{\pi}{4}\right)}{x'\left(-\frac{\pi}{4}\right)}&\mbox{}\\
&=\displaystyle \frac{\cos \left(-\frac{\pi}{4}\right)-\sin^2 \left(-\frac{\pi}{4}\right) +\cos^2 \left(-\frac{\pi}{4}\right)}{-\sin \left(-\frac{\pi}{4}\right)-2\sin \left(-\frac{\pi}{4}\right) \cos \left(-\frac{\pi}{4}\right)}&\mbox{}\\
&=\displaystyle \frac{\frac{\sqrt{2}}{2}-\left(-\frac{\sqrt{2}}{2}\right)^2 +\left(\frac{\sqrt{2}}{2}\right)^2}{-\left(-\frac{\sqrt{2}}{2}\right)-2\left(-\frac{\sqrt{2}}{2}\right) \left(\frac{\sqrt{2}}{2}\right)}&\mbox{}\\
&=\displaystyle \frac{\frac{\sqrt{2}}{2}-\frac{1}{2} +\frac{1}{2}}{\frac{\sqrt{2}}{2}+2\cdot \frac{1}{2}}&\mbox{}\\
&=\displaystyle \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}+1}&\mbox{}\\
&=\displaystyle \frac{\sqrt{2}}{\sqrt{2}+2}&\mbox{}\\
&=\displaystyle \frac{\sqrt{2}}{\sqrt{2}+2}\cdot \frac{\sqrt{2}-2}{\sqrt{2}-2}&\mbox{}\\
&=\displaystyle \frac{2-2\sqrt{2}}{2-4}&\mbox{}\\
&=\displaystyle \frac{2-2\sqrt{2}}{-2}&\mbox{}\\
&=\displaystyle \sqrt{2}-1&\mbox{}\\
&\approx \displaystyle 0.414213562&\mbox{}\\
\end{array}
$$
The slope of the tangent line is $\sqrt{2}-1,$ which is about $0.4142.$