Recall that we can model the trajectory of an package dropped from a plane:
| $ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $ |

|
We'll answer these and other questions!
Slopes of Tangent Lines of a Parametric Curve
Consider the plane curve defined by the parametric equations $x = x(t)$ and $y = y(t).$ Suppose that $x'(t)$ and $y'(t)$ exist and that $x'(t) \neq 0.$ Then $\displaystyle \frac{dy}{dx}$ is given by $$\frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{y'(t)}{x'(t)}.$$
Slopes of Tangent Lines of a Parametric Curve
Example: Find the equation of the tangent line at $t=2.$
| $ \begin{array}{l} x(t)=t^2-3\\ y(t)=2t-1 \end{array} $ |
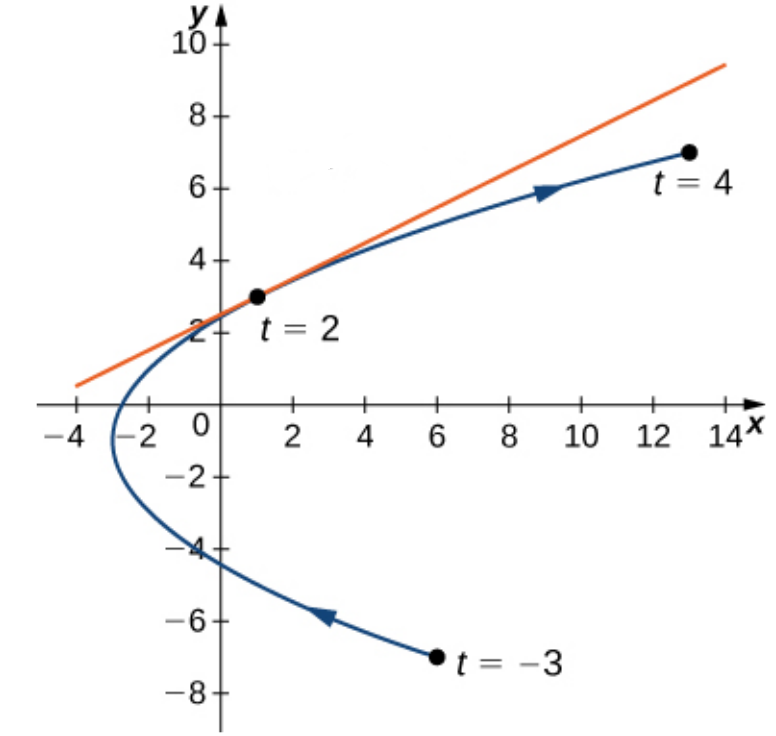
|
We first find the slope of the tangent line. The general expression for the derivative is
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}
&=\displaystyle \frac{y'(t)}{x'(t)} &\mbox{}\\
&=\displaystyle \frac{2}{2t} &\mbox{}\\
&=\displaystyle \frac{1}{t} &\mbox{}\\
\end{array}
$$
Thus,
$$
\frac{dy}{dx}\Bigr|_{t=2}=\frac{1}{2}
$$
Also, since $x(2)=2^2-3=1$ and $y(2)=2\cdot 2-1=3,$ $(1,3)$ is the ordered pair on the curve corresponding to $t=2.$
We may now find the tangent line. The point slope form of the line is, $$ y-3=\frac{1}{2}(x-1) $$ which in slope intercept form is $$ y=\frac{1}{2}x+\frac{5}{2} $$
We may now find the tangent line. The point slope form of the line is, $$ y-3=\frac{1}{2}(x-1) $$ which in slope intercept form is $$ y=\frac{1}{2}x+\frac{5}{2} $$
Slopes of Tangent Lines of a Parametric Curve
Example: Consider the trajectory of a package being dropped off by a low-flying airplane.
| $ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $ |
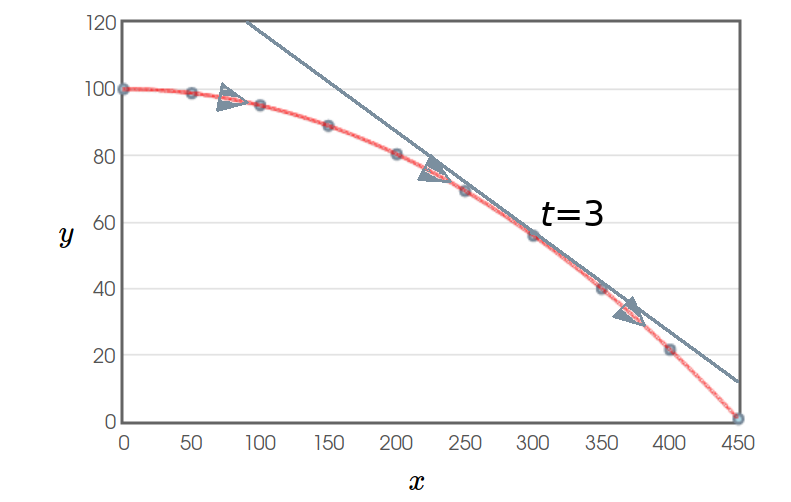
|
We first find the slope of the tangent line. The general expression for the derivative is
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dx}
&=\displaystyle \frac{y'(t)}{x'(t)} &\mbox{}\\
&=\displaystyle \frac{-9.8t}{100} &\mbox{}\\
&=\displaystyle -0.098t &\mbox{}\\
\end{array}
$$
Thus,
$$
\frac{dy}{dx}\Bigr|_{t=3}=-0.098\cdot 3=−0.294
$$
Also, since $x(3)=100\cdot 3=300$ and $y(3)=100-4.9\cdot 3^2=55.9,$ $(300,55.9)$ is the ordered pair on the curve corresponding to $t=3.$
We may now find the tangent line. The point slope form of the line is, $$ y-55.9=-0.294(x-300) $$ Then $y-55.9=-0.294x+88.2,$ or $$ y=-0.294x+144.1 $$
We may now find the tangent line. The point slope form of the line is, $$ y-55.9=-0.294(x-300) $$ Then $y-55.9=-0.294x+88.2,$ or $$ y=-0.294x+144.1 $$
Second Derivatives
Since $\displaystyle \frac{d^2 y}{dx^2}=\frac{d}{dx}\frac{dy}{dx}=\frac{dy'}{dx},$ we may simply apply the the first-derivative rule to the function $\displaystyle \frac{dy'}{dx}.$ That is $$\frac{d^2 y}{dx^2}=\frac{dy'}{dx}=\frac{dy'/dt}{dx/dt}=\frac{\frac{d}{dt}\left(\frac{dy}{dx}\right)}{\frac{dx}{dt}} =\frac{\frac{d}{dt}\left(\frac{y'(t)}{x'(t)}\right)}{x'(t)}.$$
Example: Find $\displaystyle \frac{d^2 y}{dx^2}$ when $t=2.$
| $ \begin{array}{l} x(t)=t^2-3\\ y(t)=2t-1 \end{array} $ |

|
We shall use the expression derived above to find a general expression for the second derivative.
$$
\begin{array}{lll}
\displaystyle \frac{d^2 y}{dx^2}
&=\displaystyle \frac{\frac{d}{dt}\left(\frac{y'(t)}{x'(t)}\right)}{x'(t)} &\mbox{}\\
&=\displaystyle \frac{\frac{d}{dt}\left(\frac{2}{2t}\right)}{2t} &\mbox{}\\
&=\displaystyle \frac{\frac{d}{dt}\left(\frac{1}{t}\right)}{2t} &\mbox{}\\
&=\displaystyle \frac{-\frac{1}{t^2}}{2t} &\mbox{}\\
&=\displaystyle -\frac{1}{2t^3} &\mbox{}\\
\end{array}
$$
Thus
$$
\frac{d^2y}{dx^2}\Bigr|_{t=2}=-\frac{1}{2\cdot 2^3}=-\frac{1}{16}
$$
Dire Warning
When you do this $\displaystyle \frac{d^2 y}{dx^2} = \frac{\frac{d^2 y}{dt^2}}{\frac{d^2 x}{dt^2}}=\frac{y''(t)}{x''(t)}\ldots$
YOU MAKE KITTY ANGRY!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Speed of an Object
Suppose an object's location at time $t$ is given by $$ \begin{array}{l} x=x(t)\\ y=y(t) \end{array}. $$ Then the speed of the object, $\displaystyle \frac{ds}{dt},$ is given by $$ \frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2} $$ Insight: If the moving object were equipped with a speedometer, $\frac{ds}{dt}$ is the speed that it would show.
We could also say the the above gives an object's tangential velocity.
Speed of an Object
Example: Consider the trajectory of a package being dropped off by a low-flying airplane.
| $ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $ |

|
To find $\displaystyle \frac{ds}{dt},$ we must first find $\displaystyle \frac{dx}{dt}$ and $\displaystyle \frac{dy}{dt}.$
$$
\begin{array}{lll}
\displaystyle \frac{dx}{dt}
&=\displaystyle \frac{d}{dt}100t&\mbox{}\\
&=\displaystyle 100&\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dt}
&=\displaystyle \frac{d}{dt}\left(100-4.9t^2\right)&\mbox{}\\
&=\displaystyle -9.8t&\mbox{}\\
\end{array}
$$
Then the tangential velocity at time $t$ is
$$
\frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}
=\sqrt{100^2+\left(-9.8t\right)^2}
=\sqrt{10000+96.04t^2}
$$
Thus
$$
\frac{ds}{dt}\Bigr|_{t=3}
=\sqrt{10000+96.04(3)^2}
\approx 104.2322407
$$
That is, the package's speed at $t=3$ seconds is about $104.2$ meters per second.
Speed of an Object
Example: Suppose an ant has decided to hitch a ride on the outer edge a bicycle. The ant's path will follow a cycloid curve as seen below.

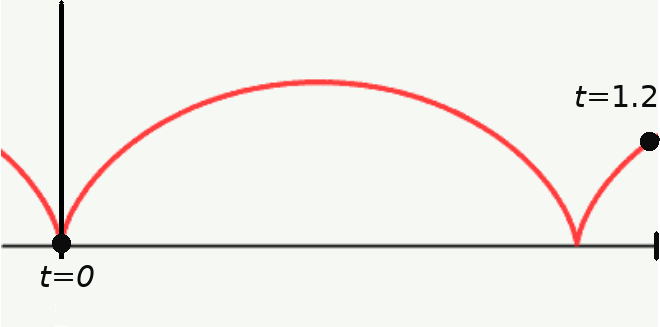
To find $\displaystyle \frac{ds}{dt},$ we must first find $\displaystyle \frac{dx}{dt}$ and $\displaystyle \frac{dy}{dt}.$
$$
\begin{array}{lll}
\displaystyle \frac{dx}{dt}
&=\displaystyle \frac{d}{dt}\left(0.35\left(\frac{2.5}{0.35} t-\sin \left(\frac{2.5}{0.35} t \right)\right)\right)&\mbox{}\\
&=\displaystyle 2.5-0.35\cos \left(\frac{2.5}{0.35} t\right)\cdot \frac{2.5}{0.35}&\mbox{}\\
&=\displaystyle 2.5-2.5\cos \left(\frac{2.5}{0.35} t\right)&\mbox{}\\
\end{array}
$$
and
$$
\begin{array}{lll}
\displaystyle \frac{dy}{dt}
&=\displaystyle \frac{d}{dt}\left(0.35\left(1-\cos \left(\frac{2.5}{0.35} t\right)\right)\right)&\mbox{}\\
&=\displaystyle 0.35\left(\sin \left(\frac{2.5}{0.35} t\right)\cdot\frac{2.5}{0.35}\right)&\mbox{}\\
&=\displaystyle 2.5 \sin \left(\frac{2.5}{0.35} t\right)&\mbox{}\\
\end{array}
$$
Then the tangential velocity at time $t$ is
$$
\frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}
=\sqrt{\left(2.5-2.5\cos \left(\frac{2.5}{0.35} t\right)\right)^2+\left(2.5 \sin \left(\frac{2.5}{0.35} t\right)\right)^2}
$$
Thus
$$
\frac{ds}{dt}\Bigr|_{t=1.2}
=\sqrt{\left(2.5-2.5\cos \left(\frac{2.5}{0.35} \cdot 1.2\right)\right)^2+\left(2.5 \sin \left(\frac{2.5}{0.35}\cdot 1.2\right)\right)^2}
\approx 4.551734722
$$
That is, the ant's speed at $t=1.2$ seconds is about $4.6$ meters per second.
The Distance Travelled by an Object
Suppose the location of an object is given by the parametric equations $$ \begin{array}{l} x=x(t)\\ y=y(t) \end{array} $$ Since the rate at which an object's distance is changing is $\frac{ds}{dt},$ the net change theorem says that the distance travelled by the object over the time interval $a \leq t \leq b$ is given by $$ \int_{a}^{b}\frac{ds}{dt}\,dt =\int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt. $$ Special Note: This is nothing more than a special case of the Net Change Theorem; an integral of a rate of change of distance gives total change in distance.
The Distance Travelled by an Object
Example: Suppose an ant has decided to hitch a ride on the outer edge a bicycle wheel. The ant's path will follow a cycloid curve as seen below.

Find how far the ant travelled over one arch of its cycloid path.
We shall first set up the integral which gives the distance travelled. Our lower limit of integration is $t=0,$
and our upper limit occurs at the first value of $t$ for which $y(t)$ is zero. That is, when
$\displaystyle 0.35\left(1-\cos \left(\frac{2.5}{0.35} t\right)\right)=0.$ Then
$$
\begin{array}{lll}
&\displaystyle \cos \left(\frac{2.5}{0.35} t\right)=1&\mbox{}\\
\implies &\displaystyle \frac{2.5}{0.35} t=2\pi&\mbox{}\\
\implies &\displaystyle t=\frac{0.35}{2.5}\cdot 2\pi&\mbox{}\\
\implies &\displaystyle t=\frac{0.7}{2.5}\pi&\mbox{}\\
\implies &\displaystyle t=\frac{7}{25}\pi&\mbox{}\\
\end{array}
$$
Also, from a previous example, we know that
$$
\frac{ds}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}
=\sqrt{\left(2.5-2.5\cos \left(\frac{2.5}{0.35} t\right)\right)^2+\left(2.5 \sin \left(\frac{2.5}{0.35} t\right)\right)^2}
$$
Thus, the distance the ant travelled is.
$$
\begin{array}{lll}
\displaystyle \int_{a}^{b}\frac{ds}{dt}\,dt
&=\displaystyle \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt&\mbox{}\\
&=\displaystyle \int_{0}^{\frac{7\pi}{25}}\sqrt{\left(2.5-2.5\cos \left(\frac{2.5}{0.35} t\right)\right)^2+\left(2.5 \sin \left(\frac{2.5}{0.35} t\right)\right)^2}\,dt&\mbox{}\\
\end{array}
$$
To simplify the notation, we will let $\omega=\frac{2.5}{0.35}$ and $r=2.5,$ and simplify the antiderivative
$$
\displaystyle \int\sqrt{\left(r\omega-r\omega\cos \left(\omega t\right)\right)^2+\left(r\omega \sin \left(\omega t\right)\right)^2}\,dt
$$
So,
$$
\begin{array}{lll}
\displaystyle \int\sqrt{\left(r\omega-r\omega\cos \left(\omega t\right)\right)^2+\left(r\omega \sin \left(\omega t\right)\right)^2}\,dt
&=\displaystyle \int\sqrt{(r\omega)^2\left(1-\cos \left(\omega t\right)\right)^2+(r\omega)^2\sin^2 \left(\omega t\right)}\,dt&\mbox{}\\
&=\displaystyle \int r\omega\sqrt{\left(1-\cos \left(\omega t\right)\right)^2+\sin^2 \left(\omega t\right)}\,dt&\mbox{}\\
&=\displaystyle r\omega\int \sqrt{1-2\cos \left(\omega t\right)+\cos^2 \left(\omega t\right)+\sin^2 \left(\omega t\right)}\,dt&\mbox{}\\
&=\displaystyle r\omega\int \sqrt{2-2\cos \left(\omega t\right)}\,dt&\mbox{}\\
&=\displaystyle r\omega\int \sqrt{4\left(\frac{1-\cos \left(\omega t\right)}{2}\right)}\,dt&\mbox{}\\
&=\displaystyle r\omega\int \sqrt{4\sin^2\left(\frac{\omega t}{2}\right)}\,dt&\mbox{trig identity}\\
&=\displaystyle r\omega\int 2\left|\sin\left(\frac{\omega t}{2}\right)\right|\,dt&\mbox{}\\
&=\displaystyle 2r\omega\int \left|\sin\left(\frac{\omega t}{2}\right)\right|\,dt&\mbox{}\\
\end{array}
$$
Thus,
$$
\begin{array}{lll}
\displaystyle \int_{a}^{b}\frac{ds}{dt}\,dt
&=\displaystyle \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt&\mbox{}\\
&=\displaystyle \int_{0}^{\frac{7\pi}{25}}\sqrt{\left(2.5-2.5\cos \left(\frac{2.5}{0.35} t\right)\right)^2+\left(2.5 \sin \left(\frac{2.5}{0.35} t\right)\right)^2}\,dt&\mbox{}\\
&=\displaystyle 2\cdot 0.35\cdot \frac{2.5}{0.35}\int_{0}^{\frac{7\pi}{25}}\left|\sin \left(\frac{2.5}{0.7} t\right)\right|\,dt&\mbox{}\\
&=\displaystyle 5\int_{0}^{\frac{7\pi}{25}}\left|\sin \left(\frac{25}{7} t\right)\right|\,dt&\mbox{}\\
\end{array}
$$
Now, $\displaystyle 0 \leq \sin\left(\frac{\omega t}{2}\right) \leq 1$ when $0 \leq \displaystyle \frac{\omega t}{2} \leq \pi,$ or
$\displaystyle 0 \leq \frac{25}{7}t \leq \pi.$
That is, when $\displaystyle 0 \leq t \leq \frac{7}{25}\pi.$
So, we may now drop the absolute value in the integral since the integrand is positive for all $t$ on the first arch.
The above becomes $$ \begin{array}{lll} \displaystyle \int_{a}^{b}\frac{ds}{dt}\,dt &=\displaystyle \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt&\mbox{}\\ &=\displaystyle 5\int_{0}^{\frac{7\pi}{25}}\left|\sin \left(\frac{25}{7} t\right)\right|\,dt&\mbox{}\\ &=\displaystyle 5 \int_{0}^{\frac{7\pi}{25}}\sin \left(\frac{25}{7} t\right)\,dt&\mbox{}\\ &=\displaystyle 5\left[-\frac{7}{25}\cos \left(\frac{25}{7} t\right)\right]_{0}^{\frac{7\pi}{25}}&\mbox{}\\ &=\displaystyle 5\cdot \frac{7}{25}\left[-\cos \left(\frac{25}{7} t\right)\right]_{0}^{\frac{7\pi}{25}}&\mbox{}\\ &=\displaystyle 1.4\left[-\cos \left(\frac{25}{7} \cdot \frac{7\pi}{25}\right)+\cos(0)\right]&\mbox{}\\ %&=\displaystyle 1.4\left[-\cos \left(\pi\right)+1\right]&\mbox{}\\ &=\displaystyle 1.4\left[-\left(-1\right)+1\right]&\mbox{}\\ &=\displaystyle 2.8&\mbox{}\\ \end{array} $$ That is, the ant travelled $2.8$ meters along one arch of its cycloid path.
$\star$$\star$$\star$ Special Note $\star$$\star$$\star$
Generally, for a wheel of any radius $r$ at angular velocity $\omega,$ one arch of the cycloid occurs over the interval $0 \leq t \leq \frac{2\pi}{\omega}$ so that that the distance $s$ travelled is $$ \begin{array}{lll} s &=\displaystyle\int_{0}^{2\pi/\omega}\frac{ds}{dt}\,dt\\ &=\displaystyle\int_{0}^{2\pi/\omega}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt\\ &=\displaystyle \int_{0}^{2\pi/\omega}\sqrt{\left(r\omega-r\omega\cos \left(\omega t\right)\right)^2+\left(r\omega \sin \left(\omega t\right)\right)^2}\,dt\\ &=\displaystyle 2r\omega\int_{0}^{2\pi/\omega} \left|\sin\left(\frac{\omega t}{2}\right)\right|\,dt&\mbox{}\\ &=\displaystyle 2r\omega\int_{0}^{2\pi/\omega} \sin\left(\frac{\omega t}{2}\right)\,dt&\mbox{since $0 \leq \sin\left(\frac{\omega t}{2}\right)\leq 1$ when $0 \leq t \leq \frac{2\pi}{\omega}$}\\ &=\displaystyle 2r\omega\left[-\frac{2}{\omega}\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 2r\omega\cdot \frac{2}{\omega}\left[-\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 4r\left[-\frac{2}{\omega}\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 4r\cdot 2&\mbox{}\\ &=\displaystyle 8r&\mbox{}\\ \end{array} $$ Thus, a point on the edge of a wheel of radius $r$ travels a distance of $8r$ along one arch of its cycloid trajectory.
The above becomes $$ \begin{array}{lll} \displaystyle \int_{a}^{b}\frac{ds}{dt}\,dt &=\displaystyle \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt&\mbox{}\\ &=\displaystyle 5\int_{0}^{\frac{7\pi}{25}}\left|\sin \left(\frac{25}{7} t\right)\right|\,dt&\mbox{}\\ &=\displaystyle 5 \int_{0}^{\frac{7\pi}{25}}\sin \left(\frac{25}{7} t\right)\,dt&\mbox{}\\ &=\displaystyle 5\left[-\frac{7}{25}\cos \left(\frac{25}{7} t\right)\right]_{0}^{\frac{7\pi}{25}}&\mbox{}\\ &=\displaystyle 5\cdot \frac{7}{25}\left[-\cos \left(\frac{25}{7} t\right)\right]_{0}^{\frac{7\pi}{25}}&\mbox{}\\ &=\displaystyle 1.4\left[-\cos \left(\frac{25}{7} \cdot \frac{7\pi}{25}\right)+\cos(0)\right]&\mbox{}\\ %&=\displaystyle 1.4\left[-\cos \left(\pi\right)+1\right]&\mbox{}\\ &=\displaystyle 1.4\left[-\left(-1\right)+1\right]&\mbox{}\\ &=\displaystyle 2.8&\mbox{}\\ \end{array} $$ That is, the ant travelled $2.8$ meters along one arch of its cycloid path.
$\star$$\star$$\star$ Special Note $\star$$\star$$\star$
Generally, for a wheel of any radius $r$ at angular velocity $\omega,$ one arch of the cycloid occurs over the interval $0 \leq t \leq \frac{2\pi}{\omega}$ so that that the distance $s$ travelled is $$ \begin{array}{lll} s &=\displaystyle\int_{0}^{2\pi/\omega}\frac{ds}{dt}\,dt\\ &=\displaystyle\int_{0}^{2\pi/\omega}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt\\ &=\displaystyle \int_{0}^{2\pi/\omega}\sqrt{\left(r\omega-r\omega\cos \left(\omega t\right)\right)^2+\left(r\omega \sin \left(\omega t\right)\right)^2}\,dt\\ &=\displaystyle 2r\omega\int_{0}^{2\pi/\omega} \left|\sin\left(\frac{\omega t}{2}\right)\right|\,dt&\mbox{}\\ &=\displaystyle 2r\omega\int_{0}^{2\pi/\omega} \sin\left(\frac{\omega t}{2}\right)\,dt&\mbox{since $0 \leq \sin\left(\frac{\omega t}{2}\right)\leq 1$ when $0 \leq t \leq \frac{2\pi}{\omega}$}\\ &=\displaystyle 2r\omega\left[-\frac{2}{\omega}\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 2r\omega\cdot \frac{2}{\omega}\left[-\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 4r\left[-\frac{2}{\omega}\cos\left(\frac{\omega t}{2}\right)\right]_{0}^{2\pi/\omega}&\mbox{}\\ &=\displaystyle 4r\cdot 2&\mbox{}\\ &=\displaystyle 8r&\mbox{}\\ \end{array} $$ Thus, a point on the edge of a wheel of radius $r$ travels a distance of $8r$ along one arch of its cycloid trajectory.
If a parametric curve does not describe the position of an object, then we simply interpret $$\displaystyle \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt$$ as arc length.
Stating this more formally...
Arc Length of a Parametric Curve
The length of a parametric curve $$ \begin{array}{l} x=x(t)\\ y=y(t) \end{array} $$ when $a \leq t\leq b$ is given by $$ \int_{a}^{b}\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}\,dt. $$
Special Note
To calculate how far the ant travelled in our previous example, we could have simply used the parameterization of the cycloid which does not depend on time $t$ but on the angle $\theta.$
That is, we could have calculated the arc length of the cycloid curve $$ \begin{array}{l} x(\theta)=r(\theta-\sin \theta)\\ y(\theta)=r(1-\cos \theta) \end{array} $$ over $0 \leq \theta \leq 2\pi$ as $$ \int_{0}^{2\pi}\sqrt{\left(\frac{dx}{d\theta}\right)^2+\left(\frac{dy}{d\theta}\right)^2}\,d\theta=8r. $$
Arc Length
Example: State the arc length of the curve below as an integral.

The interval of integration is $-2 \leq t \leq 3,$ $x'(t)=2t,$ and $y'(t)=2.$
The arc length of the above curve is then given by
$$
\int_{-2}^{3}\sqrt{\left(2t\right)^2+\left(2\right)^2}\,dt=\int_{-2}^{3}\sqrt{4t^2+4}\,dt=2\int_{-2}^{3}\sqrt{t^2+1}\,dt
$$
Areas Under Parametric Curves
The area under a parametric curve $$ \begin{array}{l} x=x(t)\\ y=y(t) \end{array} $$ when $a \leq t\leq b$ is given by $$ \int_{a}^{b}y(t)x'(t)dt. $$
Areas Under Parametric Curves: A Justification
If $y$ is a function of $x,$ then perhaps it's no surprise that the area under the curve of this function from $c$ to $d$ is given by $$ \int_{c}^{d}y\, dx. $$ But since $y$ and $x$ both depend on $t,$ that is $x=x(t)$ and $y=y(t).$ Thus, by the method of substitution $dx=x'(t) \,dt$ so that $$ \int_{c}^{d}y \, dx=\int_{a}^{b} y(t) x'(t)\, dt $$ where $c \leq x \leq d$ and $a \leq t \leq b.$
Area Under a Parametric Curve
Example: Suppose an ant has decided to hitch a ride on the outer edge a bicycle wheel. The ant's path will follow a cycloid curve as seen below.

Taking previous examples as a hint, we shall find the area under one arch of a general cycloid curve for a wheel of radius $r$
$$
\begin{array}{l}
x(\theta)=r(\theta-\sin \theta)\\
y(\theta)=r(1-\cos \theta)
\end{array}
$$
and apply the general result to our particular situation.
We note that $x'(\theta)=r(1-\cos \theta)$ so that the area under one arch of the cycloid curve is given by
$$
\begin{array}{lll}
\displaystyle \int_{0}^{2\pi} y(\theta) x'(\theta)\, d\theta
&=\displaystyle \int_{0}^{2\pi} r(1-\cos \theta)\cdot r(1-\cos \theta)\, d\theta&\mbox{}\\
&=\displaystyle r^2\int_{0}^{2\pi} (1-\cos\theta)^2 \, d\theta&\mbox{}\\
&=\displaystyle r^2\int_{0}^{2\pi} 1-2\cos\theta+\cos^2 \theta \, d\theta&\mbox{}\\
&=\displaystyle r^2\int_{0}^{2\pi} 1-2\cos\theta+\frac{1+\cos(2\theta)}{2} \, d\theta&\mbox{}\\
&=\displaystyle r^2 \left[\theta-2\sin\theta+\frac{\theta}{2}+\frac{\sin(2\theta)}{4}\right]_{0}^{2\pi}&\mbox{}\\
&=\displaystyle r^2 \left[2\pi+\pi\right]&\mbox{}\\
&=\displaystyle 3\pi r^2&\mbox{}\\
\end{array}
$$
Thus, for the ant riding along a wheel of radius $r=0.35$ meters, the area under the path swept out by the ant is
$$
3\pi r^2=3\pi (0.35)^2\approx 1.15 \mbox{ square meters}
$$