Recall that we can model the position of the height of a free-falling object in one dimension. For example, $s(t)=-4.9t^2+100$ models the height of an object dropped from $100$ meters.
Big Question: What if we wanted to model the position of an object in two dimensions?
Parametric Equations & Curves
Big Answer: Parametric Equations!
Parametric Equations & Curves
Example: Consider the set of equations which give $x$ and $y$ as a function of a parameter $t.$ $$ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $$
Parametric Equations & Curves
$$ \begin{array}{|c|c|c|} \hline t & x & y \\ \hline 0 & 0 & 100\\ \hline 0.5 & 50 & 98.775 \\ \hline 1 & 100 & 95.1 \\ \hline 1.5 & 150 & 88.975 \\ \hline 2 & 200 & 80.4 \\ \hline 2.5 & 250 & 69.375 \\ \hline 3 & 300 & 55.9 \\ \hline 3.5 & 350 & 39.975 \\ \hline 4 & 400 & 21.6 \\ \hline 4.5 & 450 & 0.775 \\ \hline \end{array} $$
Parametric Equations & Curves

Parametric Equations & Curves $$ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $$

Curves defined parametrically have an orientation which is the direction $x$ and $y$ move as the parameter $t$ increases.
Parametric Equations & Curves
Definition: If $x$ and $y$ are continuous functions of $t$ on an interval $I,$ then the equations $$x = x(t) \,\,\mbox{ and }\,\, y = y(t)$$ are called parametric equations and $t$ is called the parameter. The set of points $(x, y)$ obtained as $t$ varies over the interval $I$ is called the graph of the parametric equations. The graph of parametric equations is called a parametric curve or plane curve, and is denoted by $C.$
Parametric Equations & Curves: Example
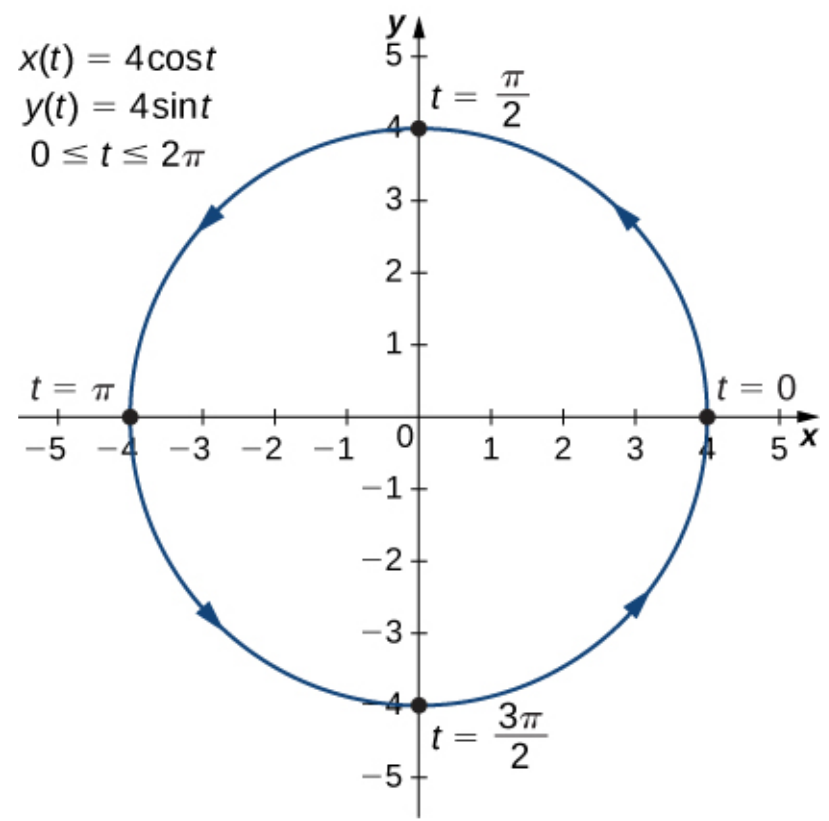
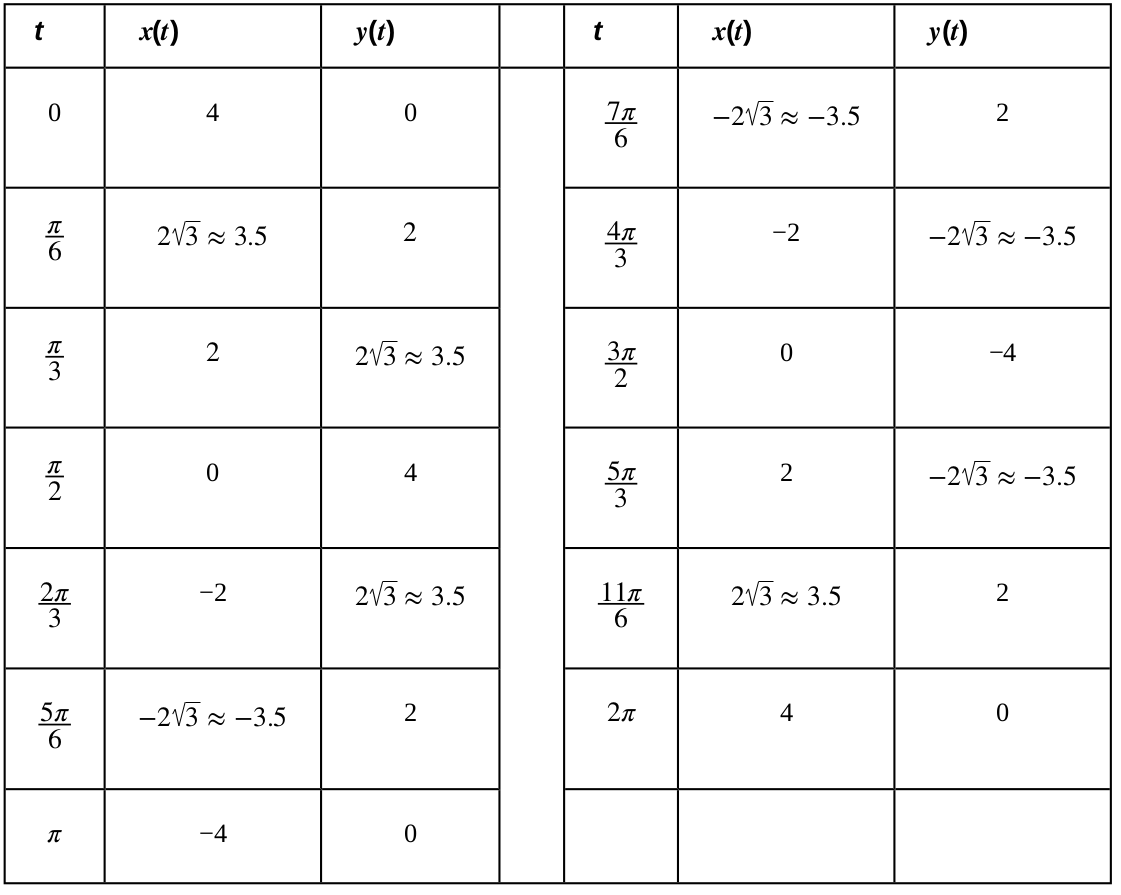
Parametric Equations & Curves: Example

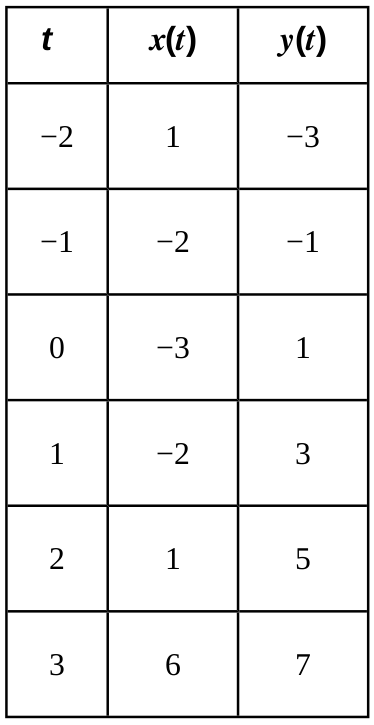
Parametric Equations & Curves: Example
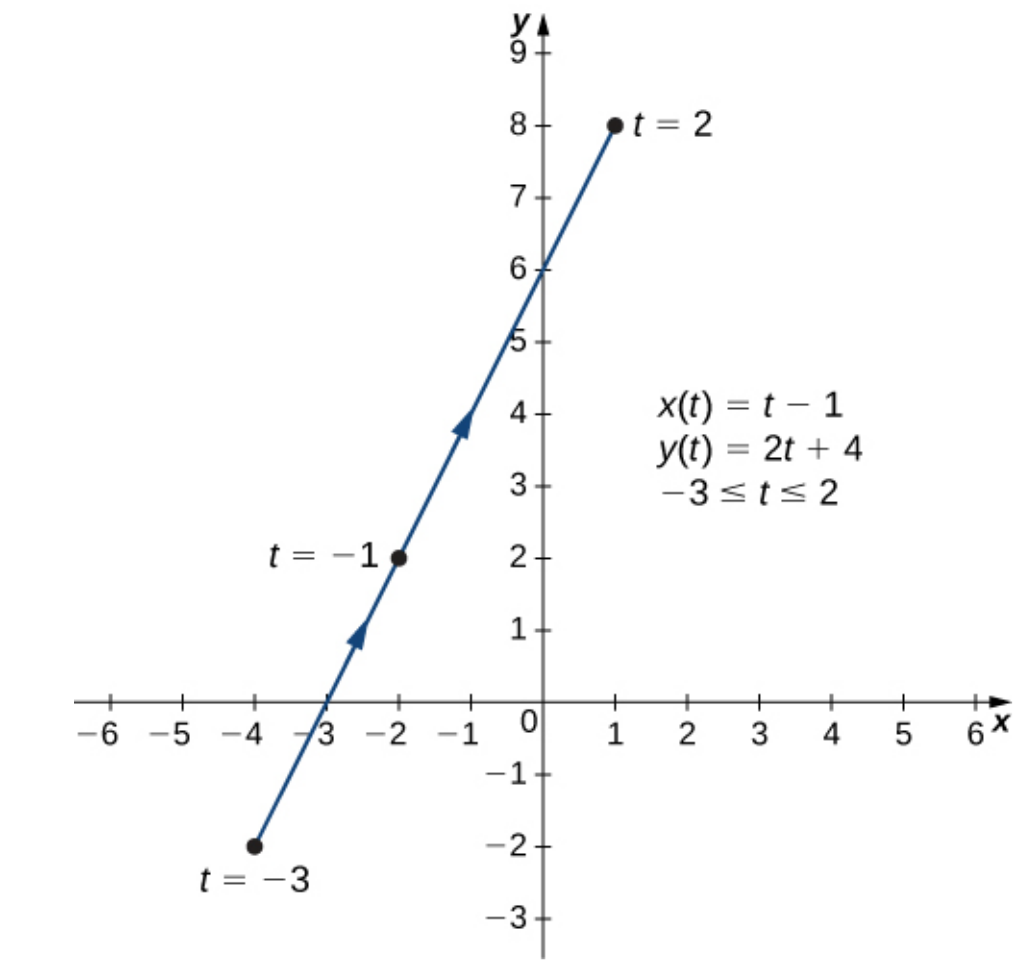
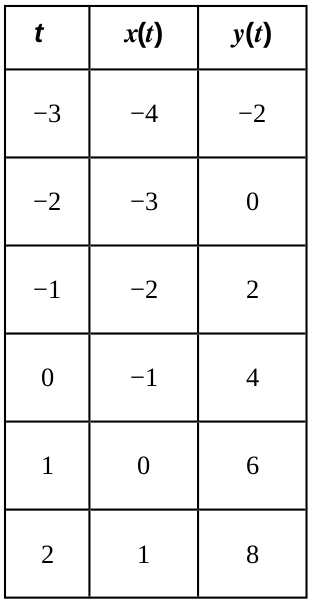
Parametric Equations & Curves
Setting up a table is a sure-fire way to graph a set of parametric equations.
But there are other ways to know what the curve will look like.
One way is to eliminate the parameter.
Eliminating the Parameter
Example: Eliminate the parameter $t$ in the set of parametric equations below to obtain a direct relationship between $x$ and $y.$ $$ \begin{array}{l} x(t)=100t\\ y(t)=100-4.9t^2 \end{array} $$

The first equation is $x(t)=100t.$ Then $\displaystyle t=\frac{x(t)}{100}.$ Substituting into the second equation,
$$
y(t)=100-4.9\left(\frac{x(t)}{100}\right)^2
$$
We may now drop the $t$ (eliminate the parameter!) since it is no longer explicit, we simplify and rewrite the above as
$
y=100-\frac{4.9}{10000}x^2
$
which becomes
$$
y=100-0.00049x^2
$$
Eliminating the Parameter
Example: Eliminate the parameter $t$ in the set of parametric equations below to obtain a direct relationship between $x$ and $y.$

To eliminate the parameter, we shall attempt to express $y(t)$ in terms of $x(t).$
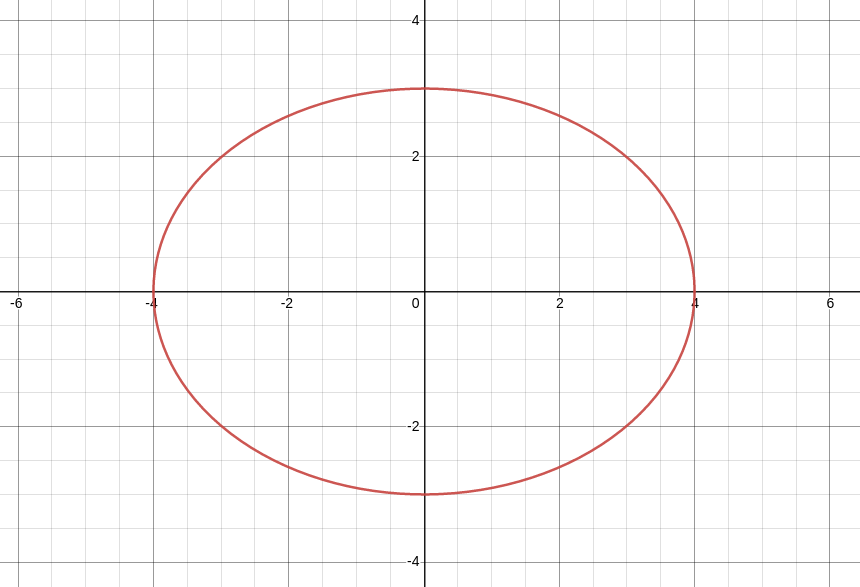
We first recall the Pythagorean Identity relating $\sin(t)$ and $\cos(t)$ $$\cos^2(t)+\sin^2(t)=1$$ It follows that $$16\cos^2(t)+16\sin^2(t)=16$$ But since $x(t)=4\cos(t)$ and $y(t)=4\sin(t),$ the above can be written as $$x(t)^2+y(t)^2=16$$ which is the same as saying $$x^2+y^2=16$$
We first recall the Pythagorean Identity relating $\sin(t)$ and $\cos(t)$ $$\cos^2(t)+\sin^2(t)=1$$ It follows that $$16\cos^2(t)+16\sin^2(t)=16$$ But since $x(t)=4\cos(t)$ and $y(t)=4\sin(t),$ the above can be written as $$x(t)^2+y(t)^2=16$$ which is the same as saying $$x^2+y^2=16$$
Eliminating the Parameter
Example: Eliminate the parameter $t$ in the set of parametric equations below to obtain a direct relationship between $x$ and $y.$

We'll first solve for $t$ in the second equation $y(t)=2t+1$ to get
$$
t=\frac{y(t)-1}{2}
$$
Substituting $t$ into the first equation we have
$$
x(t)=\left(\frac{y(t)-1}{2}\right)^2-3
$$
Since the parameter has now been eliminated, we drop the $t$ and simplify.
$$
\begin{array}{lll}
&\displaystyle x=\left(\frac{y-1}{2}\right)^2-3 &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y+1}{4}-3 &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y+1-12}{4} &\mbox{}\\
\implies &\displaystyle x=\frac{y^2-2y-11}{4} &\mbox{}\\
\implies &\displaystyle x=\frac{1}{4}y^2-\frac{1}{2}y-\frac{11}{4} &\mbox{}\\
\end{array}
$$
Eliminating the Parameter
Example: Eliminate the parameter $t$ in the set of parametric equations below to obtain a direct relationship between $x$ and $y.$ $$ \begin{array}{l} x(t)=4 \cos t\\ y(t)=3 \sin t \end{array} $$
We will use the Pythagorean Identity again, but we must first solve for $\cos t$ and $\sin t$ in the above equations.
$$
\begin{array}{l}
\frac{x(t)}{4}= \cos t\\
\frac{y(t)}{3}= \sin t
\end{array}
$$
Then,
$$
\left(\frac{x(t)}{4}\right)^2+\left(\frac{y(t)}{3}\right)^2=\cos^2 t+\sin^2 t=1
$$
or
$$
\frac{x^2}{16}+\frac{y^2}{9}=1
$$
which is the equation of an ellipse.

More Complex Curves: The Cycloid
Example: The cycloid is the curve determined by a point on the outer edge of a rolling wheel.

Let's derive the parametric equations for this curve. We'll assume the radius of the circle is $r.$
We are going to give $x$ and $y$ in terms of the angle $\theta$ the wheel rolls through. Notice that $\theta$ will be the parameter in this case.
We first sketch a picture of the situation.
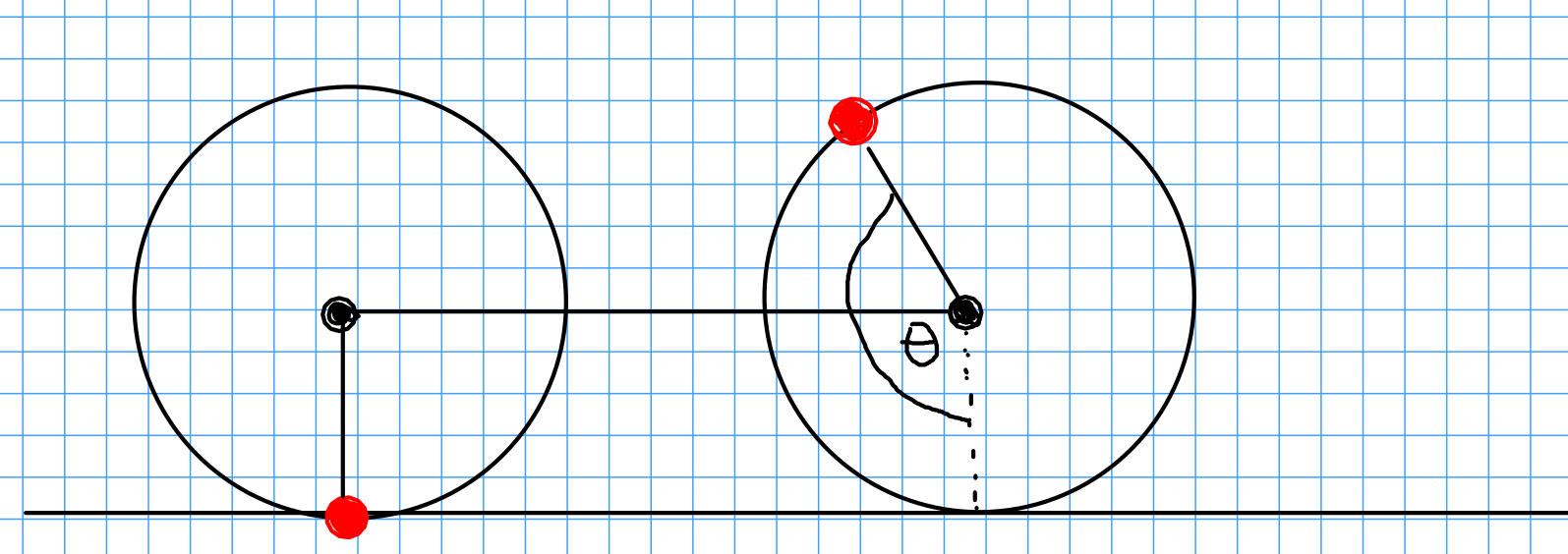
The key thing to notice is that the horizontal distance the wheel has rolled is the same as the the length of tread rolled on the wheel.
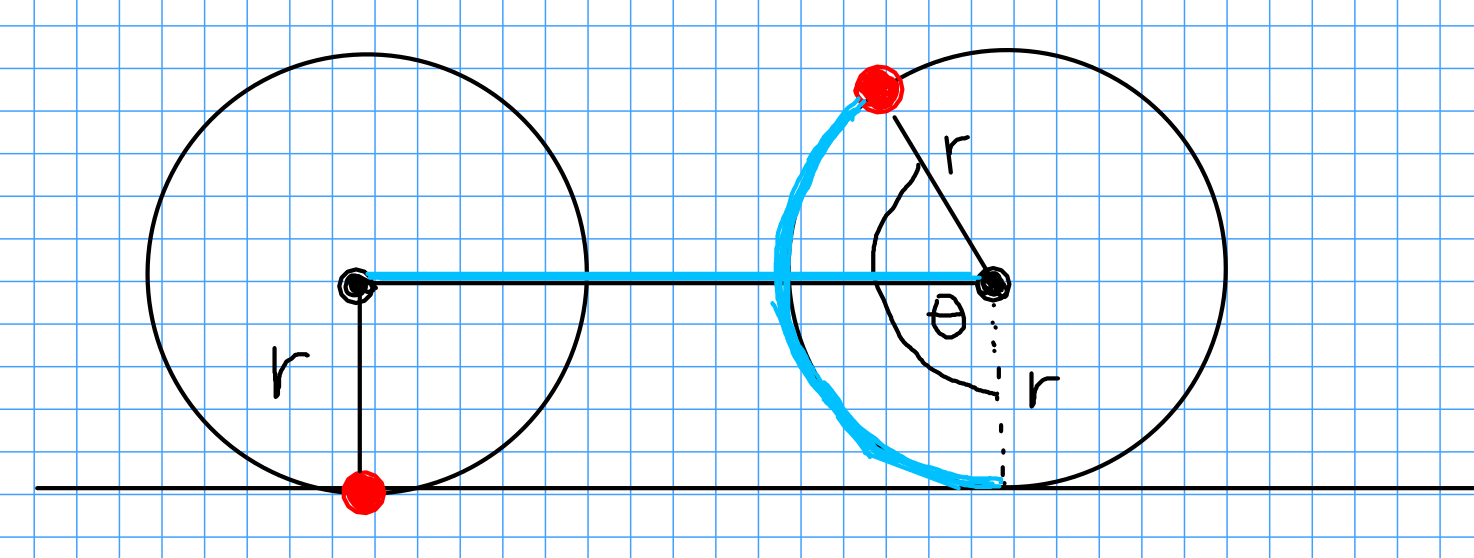
Since the the arc length $s$ of a circle made through an angle $\theta$ is given by $s=r\theta,$ we have that the center of the wheel is modelled by the equations $$ \begin{array}{l} x(\theta)=r\theta\\ y(\theta)=r \end{array} $$ Now, if the red point was on a circle of radius $r$ centered at the origin, its coordinates would be given by $$ \begin{array}{l} x(\theta)=r\cos\left(-\frac{\pi}{2}-\theta\right)\\ y(\theta)=r\sin\left(-\frac{\pi}{2}-\theta\right) \end{array} $$ which, after a healthy dose of either identities or transformations, become $$ \begin{array}{l} x(\theta)=-r\sin \theta \\ y(\theta)=-r\cos \theta \end{array} $$ Re-centering the circle at its actual position, $(r\theta,r)$ given above, the true position of the red dot is now $$ \begin{array}{l} x(\theta)=r\theta-r\sin \theta\\ y(\theta)=r-r\cos \theta \end{array} $$ These are the parametric equations which describe the cycloid curve.

The key thing to notice is that the horizontal distance the wheel has rolled is the same as the the length of tread rolled on the wheel.

Since the the arc length $s$ of a circle made through an angle $\theta$ is given by $s=r\theta,$ we have that the center of the wheel is modelled by the equations $$ \begin{array}{l} x(\theta)=r\theta\\ y(\theta)=r \end{array} $$ Now, if the red point was on a circle of radius $r$ centered at the origin, its coordinates would be given by $$ \begin{array}{l} x(\theta)=r\cos\left(-\frac{\pi}{2}-\theta\right)\\ y(\theta)=r\sin\left(-\frac{\pi}{2}-\theta\right) \end{array} $$ which, after a healthy dose of either identities or transformations, become $$ \begin{array}{l} x(\theta)=-r\sin \theta \\ y(\theta)=-r\cos \theta \end{array} $$ Re-centering the circle at its actual position, $(r\theta,r)$ given above, the true position of the red dot is now $$ \begin{array}{l} x(\theta)=r\theta-r\sin \theta\\ y(\theta)=r-r\cos \theta \end{array} $$ These are the parametric equations which describe the cycloid curve.
More Complex Curves: The Cycloid
Example: The cycloid is the curve determined by a point on the outer edge of a rolling wheel.

More Complex Curves: Hypocycloids
A hypocycloid is the curve determined by a point on the outer edge of a rolling wheel rolling inside a circle.
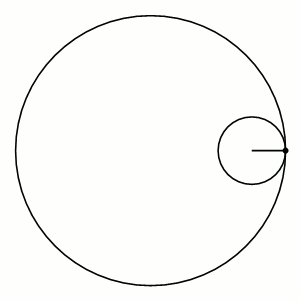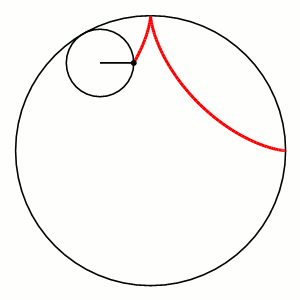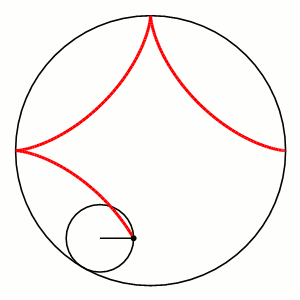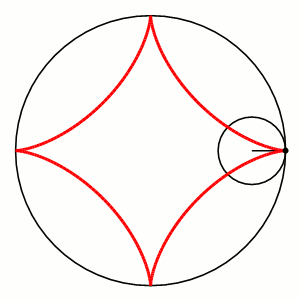
More Complex Curves: Hypocycloids
Example

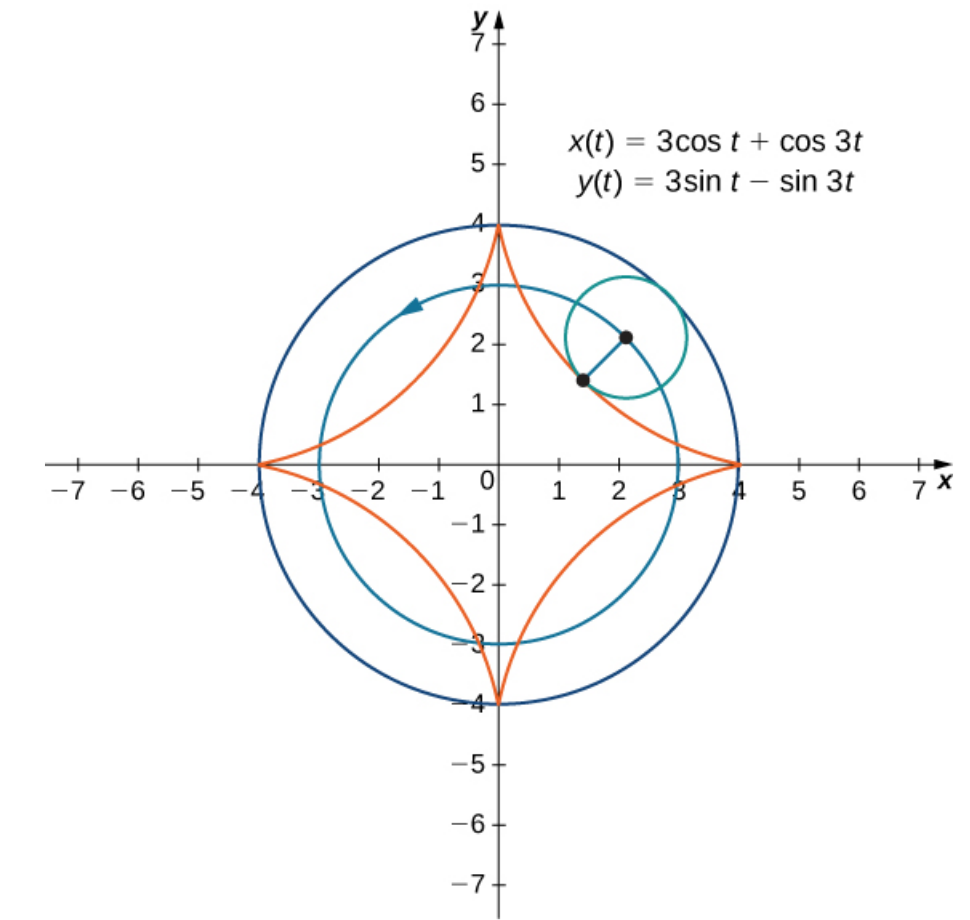
More Complex Curves: Hypocycloids
With a larger outer circle of radius $R$ and a smaller inner circle of radius $r,$ the equations for the hypocycloid are given by $$ \begin{array}{l} x(\theta)=(R-r)\cos \theta + r \cos \left(\frac{R-r}{r}\theta \right)\\ y(\theta)=(R-r)\sin \theta - r \sin \left(\frac{R-r}{r}\theta \right)\\ \end{array} $$
More Complex Curves: The Hypotrochoid (Spirograph)
A hypotrochoid is the curve determined by a point on the interior of a rolling wheel rolling inside a circle.

More Complex Curves: The Hypotrochoid (Spirograph)
With a larger outer circle of radius $R$ and a smaller inner circle of radius $r,$ and a point a distance $d$ away from the center of the smaller circle, the equations for the hypotrochoid (spirograph) are given by $$ \begin{array}{l} x(\theta)=(R-r)\cos \theta + d \cos \left(\frac{R-r}{r}\theta \right)\\ y(\theta)=(R-r)\sin \theta - d \sin \left(\frac{R-r}{r}\theta \right)\\ \end{array} $$
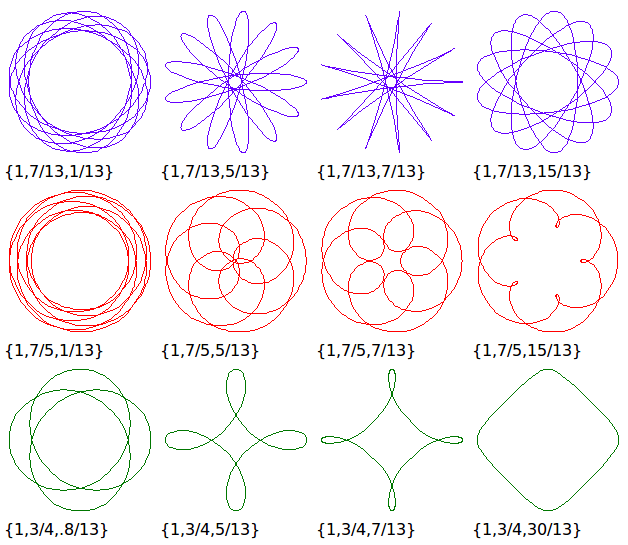
My Own Spirograph Curves
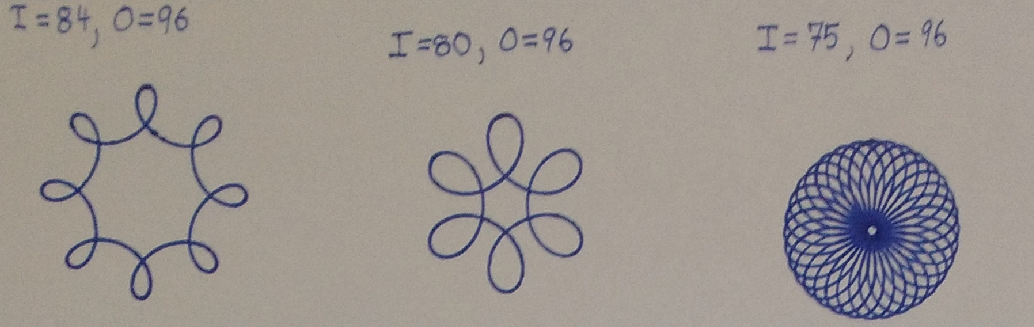

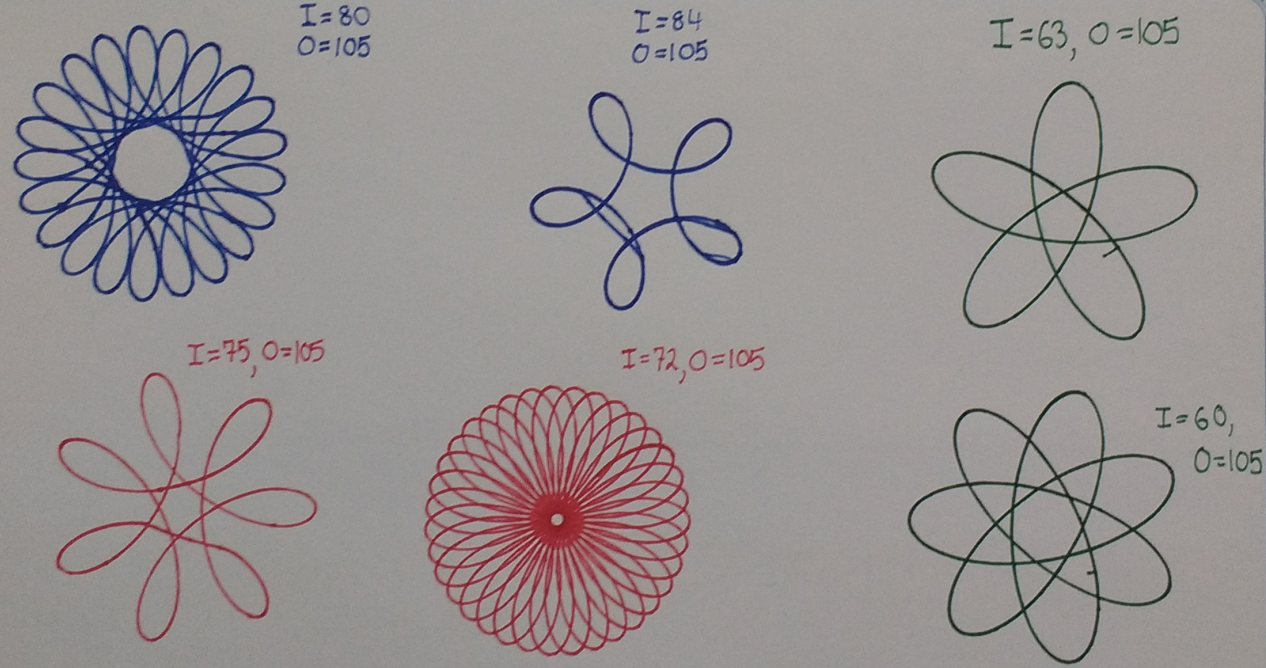
More Complex Curves: The Hypotrochoid (Spirograph)
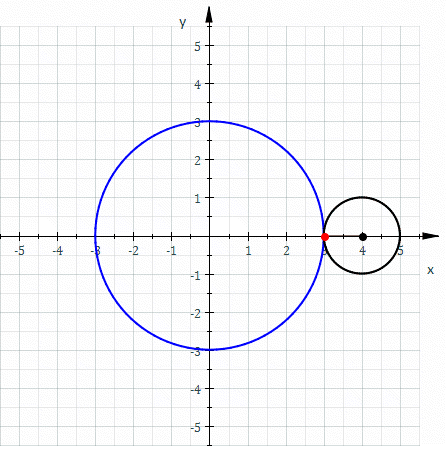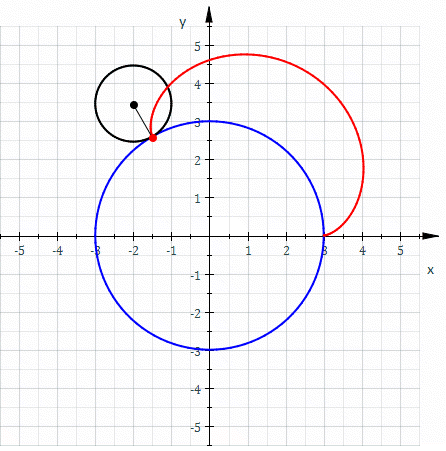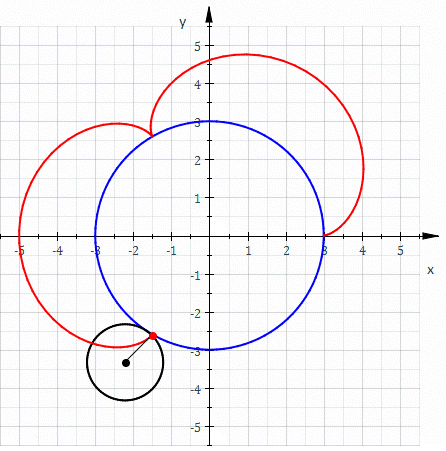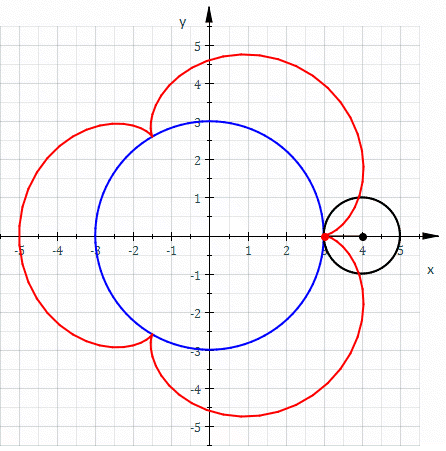
Example: Consider the spirograph curve below.

More Variations!
| Epicycloid | Epitrochoid (Outer Spirograph) | Hyporochoid (Point not on Inner Circle) |
 |  | 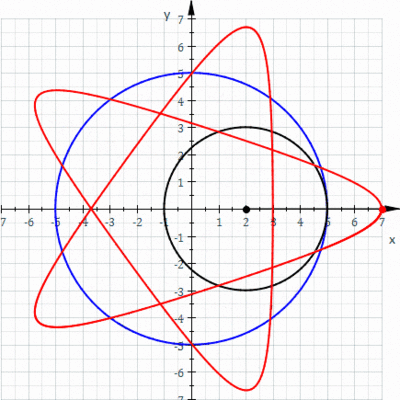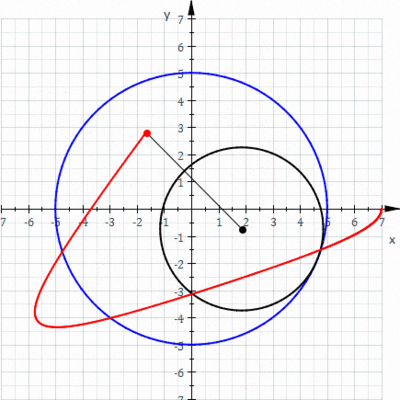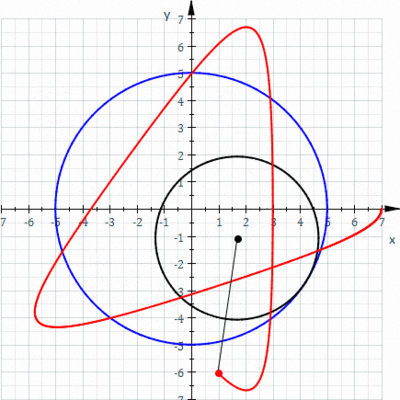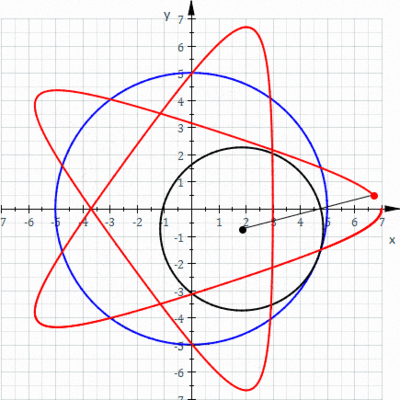 |
| ${\small \begin{array}{c} x(\theta)=(R+r)\cos \theta - d \cos \left(\frac{R+r}{r}\theta \right)\\ y(\theta)=(R+r)\sin \theta - d \sin \left(\frac{R+r}{r}\theta \right)\\ d=r \end{array}} $ | ${\small \begin{array}{c} x(\theta)=(R+r)\cos \theta - d \cos \left(\frac{R+r}{r}\theta \right)\\ y(\theta)=(R+r)\sin \theta - d \sin \left(\frac{R+r}{r}\theta \right)\\ d \lt r \end{array}} $ | ${\small \begin{array}{c} x(\theta)=(R-r)\cos \theta + d \cos \left(\frac{R-r}{r}\theta \right)\\ y(\theta)=(R-r)\sin \theta - d \sin \left(\frac{R-r}{r}\theta \right)\\ d > r \end{array}} $ |