Today we shall be able to find series representations for a much broader class of functions than rational functions.
In doing so, we will begin to understand deep connections between certain types of functions.
We will see that series representations of functions will reveal their truest nature.
Taylor and Maclaurin Series: The Germ of the Idea
The derivatives of a series representation $\displaystyle \sum_{n=0}^{\infty}c_nx^n$ and $f(x)$ should all be the same at $x=a.$
The function $\displaystyle f(x)=\frac{1}{1-x}$ can be represented by the power series $\displaystyle \sum_{n=0}^{\infty}x^n$ on the interval $(-1,1).$
This is All to Say That...
For a power series representation $\displaystyle \sum_{n=0}^{\infty}c_n(x-a)^n$ of $f(x):$
$f(a)$ should equal $\displaystyle \sum_{n=0}^{\infty}c_n(a-a)^n=c_0$
$f'(a)$ should equal $\displaystyle \sum_{n=1}^{\infty}c_n n(a-a)^{n-1}=c_1$
$f''(a)$ should equal $\displaystyle \sum_{n=2}^{\infty}c_n n(n-1)(a-a)^{n-2}=2c_2$
$f'''(a)$ should equal $\displaystyle \sum_{n=3}^{\infty}c_n n(n-1)(n-2)(a-a)^{n-3}=3 \cdot 2 c_3$
$f^{(4)}(a)$ should equal $\displaystyle \sum_{n=4}^{\infty}c_n n(n-1)(n-2)(n-3)(a-a)^{n-4}=4 \cdot 3 \cdot 2 c_4$
$\vdots$
Generally Speaking...
For a power series representation $\displaystyle \sum_{n=0}^{\infty}c_n(x-a)^n$ of $f(x):$
$f^{(k)}(a)$ should equal $\displaystyle \sum_{n=k}^{\infty}c_n k(n-1)(n-2)(n-3)\cdots 1(a-a)^{n-k}=k! c_k.$
In other words the $k$th derivative of $f(x)$ should be the same as the $k$th derivative of the power series representation.
Rewriting the above, we get the coefficients $\displaystyle c_k=\frac{f^{(k)}(a)}{k!}.$
Taylor Series
If $f(x)$ has derivatives of all orders at $x = a,$ then the Taylor series expansion for the function $f(x)$ at $a$ is $$\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$$ The Taylor series for $f(x)$ at $a=0$ is known as the Maclaurin series for $f(x).$
An Important Result
If a function $f$ has a power series at $a$ that converges to $f$ on some open interval containing $a,$ then that power series is the Taylor series for $f$ at $a.$
Example
Since $\displaystyle f(x)=\frac{1}{1-x}=\sum_{n=0}^{\infty}x^n$ on the interval $(-1,1),$ we may conclude that $\displaystyle \sum_{n=0}^{\infty}x^n$ is the Taylor series for $\displaystyle f(x)=\frac{1}{1-x}$ at $0.$
Taylor Polynomials
If $f(x)$ has $N$ derivatives at $x = a,$ then the $N$th Taylor polynomial $p_N(x)$ for $f$ at $a$ is $$\displaystyle p_N(x)=\sum_{n=0}^{N}\frac{f^{(n)}(a)}{n!}(x-a)^n$$ The $N$th Taylor polynomial for $f$ at $0$ is known as the $N$th Maclaurin polynomial for $f.$
Example
Find the Maclaurin series expansion of $f(x)=\sin x.$
Determine the radius of convergence.
We first note that
$$
\begin{array}{lll}
f(x)&=&\sin x\\
f'(x)&=&\cos x\\
f''(x)&=&-\sin x\\
f'''(x)&=&-\cos x\\
f^{(4)}(x)&=&\sin x\\
f^{(5)}(x)&=&\cos x\\
f^{(6)}(x)&=&-\sin x\\
f^{(7)}(x)&=&-\cos x\\
&\vdots&
\end{array}
$$
Thus, the coefficients of the Maclaurin series expansion are
$$
\begin{array}{lll}
\displaystyle c_0&=\displaystyle \frac{f^{(0)}(0)}{0!}=f(0)=\sin 0 =0\\
\displaystyle c_1&=\displaystyle \frac{f^{(1)}(0)}{1!}=f'(0)=\cos 0 =1\\
\displaystyle c_2&=\displaystyle \frac{f^{(2)}(0)}{2!}=\frac{f''(0)}{2}=\frac{-\sin 0}{2} =0\\
\displaystyle c_3&=\displaystyle \frac{f^{(3)}(0)}{3!}=\frac{f'''(0)}{3!}=\frac{-\cos 0}{3!} =-\frac{1}{3!}\\
\displaystyle c_4&=\displaystyle \frac{f^{(4)}(0)}{4!}=\frac{\sin 0}{4!} =0\\
\displaystyle c_5&=\displaystyle \frac{f^{(5)}(0)}{5!}=\frac{\cos 0}{5!} =\frac{1}{5!}\\
\displaystyle c_6&=\displaystyle \frac{f^{(6)}(0)}{6!}=\frac{-\sin 0}{6!} =\frac{0}{6!}=0\\
\displaystyle c_7&=\displaystyle \frac{f^{(7)}(0)}{7!}=\frac{-\cos 0}{7!} =-\frac{1}{7!}\\
&\vdots&
\end{array}
$$
The Maclaurin series expansion is then
$$
\begin{array}{lll}
\displaystyle \sin x&=\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^{n}\\
&=\displaystyle \frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5+\cdots+\frac{f^{(k)}(0)}{k!}x^k+\cdots&\\
&=\displaystyle 0+x+0x^2-\frac{1}{3!}x^3+0x^4+\frac{1}{5!}x^5+0x^6-\frac{1}{7!}x^7+\cdots&\\
&=\displaystyle x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots&\\
&=\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1}&\\
\end{array}
$$
To determine the radius of convergence, $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{(-1)^{n+1}}{(2(n+1)+1)!}x^{2(n+1)+1}}{\frac{(-1)^n}{(2n+1)!}x^{2n+1}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{(-1)^{n+1}}{(2n+3)!}x^{2n+3}}{\frac{(-1)^n}{(2n+1)!}x^{2n+1}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{(-1)^{n+1}}{(2n+3)!}x^{2}}{\frac{(-1)^n}{(2n+1)!}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(-1)^{n+1}}{(2n+3)!}\cdot \frac{(2n+1)!}{(-1)^n}x^{2}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{1}{(2n+2)(2n+3)}x^{2}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{1}{(2n+2)(2n+3)}\right|\left|x^{2}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\frac{1}{(2n+2)(2n+3)}x^{2} &\mbox{}\\
&=\displaystyle x^{2}\lim_{n \rightarrow \infty}\frac{1}{(2n+2)(2n+3)} &\mbox{}\\
&=\displaystyle x^2\cdot 0&\mbox{}\\
&\lt \displaystyle 1 &\mbox{}\\
\end{array}
$$
Since the above inequality is satisfied for all $x,$ the radius of convergence is $R=\infty$ and the series converges absolutely on $(-\infty,\infty).$
Example: The function $\displaystyle f(x)=\sin x$ can be represented by the power series $\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1}.$
Example
Find the Maclaurin series expansion of $f(x)=e^x.$
Determine the radius of convergence.
We first note that
$$
\begin{array}{lll}
f(x)&=&e^x\\
f'(x)&=&e^x\\
f''(x)&=&e^x\\
f'''(x)&=&e^x\\
f^{(4)}(x)&=&e^x\\
&\vdots&\\
f^{(k)}(x)&=&e^x\\
\end{array}
$$
Thus, $f^{(n)}(0)=1$ for all $n.$
The Maclaurin series expansion is then
$$
\begin{array}{lll}
\displaystyle e^x&=\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(0)}{n!}x^{n}\\
&=\displaystyle \frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5+\cdots+\frac{f^{(k)}(0)}{k!}x^k+\cdots&\\
&=\displaystyle \frac{1}{0!}+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\frac{1}{5!}x^5+\cdots+\frac{1}{k!}x^k+\cdots&\\
&=\displaystyle \sum_{n=0}^{\infty}\frac{1}{n!}x^{n}&\\
\end{array}
$$
To determine the radius of convergence, $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{1}{(n+1)!}x^{n+1}}{\frac{1}{n!}x^{n}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{n!}{(n+1)!}x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{1}{n+1}x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\frac{1}{n+1}\left|x\right| &\mbox{}\\
&=\displaystyle \left|x\right|\lim_{n \rightarrow \infty}\frac{1}{n+1} &\mbox{}\\
&=\displaystyle \left|x\right|\cdot 0 &\mbox{}\\
&\lt \displaystyle 1 &\mbox{}\\
\end{array}
$$
Since the above inequality is satisfied for all $x,$ the radius of convergence is $R=\infty$ and the series converges absolutely on $(-\infty,\infty).$
Example: The function $\displaystyle f(x)=e^x$ can be represented by the power series $\displaystyle \sum_{n=0}^{\infty}\frac{1}{n!}x^{n}.$
Example
Find the Taylor series expansion of $f(x)=\ln(x)$ at $x=1.$
Determine the radius of convergence.
We first note that
$$
\begin{array}{lll}
f(x)&=&\ln x\\
f'(x)&=&\displaystyle \frac{1}{x}=\frac{0!}{x}\\
f''(x)&=&\displaystyle -\frac{1}{x^2}=-\frac{1!}{x^2}\\
f'''(x)&=&\displaystyle \frac{2}{x^3}=\frac{2!}{x^3}\\
f^{(4)}(x)&=&\displaystyle -\frac{2\cdot 3}{x^4}=-\frac{3!}{x^4}\\
f^{(5)}(x)&=&\displaystyle \frac{2\cdot 3\cdot 4}{x^5}=\frac{4!}{x^5}\\
f^{(6)}(x)&=&\displaystyle -\frac{2\cdot 3\cdot 4\cdot 5}{x^6}=-\frac{5!}{x^6}\\
f^{(7)}(x)&=&\displaystyle \frac{2\cdot 3 \cdot 4 \cdot 5 \cdot 6}{x^7}=\frac{6!}{x^7}\\
&\vdots&
\end{array}
$$
Thus, $\displaystyle f^{(n)}(x)=(-1)^{n+1}\frac{(n-1)!}{x^n}$ for $n \geq 1.$
Since we're expanding at $x=1,$ we have $\displaystyle f^{(n)}(1)=(-1)^{n+1}(n-1)!$ for $n\geq 1.$
The Taylor series expansion around $x=1$ is then $$ \begin{array}{lll} \displaystyle \ln x&=\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(1)}{n!}(x-1)^{n}\\ &=\displaystyle \frac{f(1)}{0!}+\frac{f'(1)}{1!}(x-1)+\frac{f''(1)}{2!}(x-1)^2+\frac{f'''(1)}{3!}(x-1)^3+\frac{f^{(4)}(1)}{4!}(x-1)^4+\frac{f^{(5)}(1)}{5!}(x-1)^5+\cdots&\\ &=\displaystyle \frac{0}{1}+\frac{0!}{1!}(x-1)-\frac{1!}{2!}(x-1)^2+\frac{2!}{3!}(x-1)^3-\frac{3!}{4!}(x-1)^4+\frac{4!}{5!}(x-1)^5-\cdots&\\ &=\displaystyle (x-1)-\frac{1}{2}(x-1)^2+\frac{1}{3}(x-1)^3-\frac{1}{4}(x-1)^4+\frac{1}{5}(x-1)^5-\cdots&\\ &=\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}(x-1)^{n}&\\ \end{array} $$ To determine the radius of convergence, $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$ $$ \begin{array}{lll} \displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right| &=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{(-1)^{n+2}}{n+1}(x-1)^{n+1}}{\frac{(-1)^{n+1}}{n}(x-1)^{n}}\right| &\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{n}{n+1}(x-1)\right| &\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\frac{n}{n+1}\left|x-1\right| &\mbox{}\\ &=\displaystyle \left|x-1\right|\lim_{n \rightarrow \infty}\frac{n}{n+1} &\mbox{}\\ &=\displaystyle \left|x-1\right| &\mbox{}\\ &\lt \displaystyle 1 &\mbox{}\\ \end{array} $$ Thus, the series converges absolutely when $|x-1|\lt 1,$ and the radius of convergence is $R=1.$
The series converges absolutely on $(0,2).$
Since we're expanding at $x=1,$ we have $\displaystyle f^{(n)}(1)=(-1)^{n+1}(n-1)!$ for $n\geq 1.$
The Taylor series expansion around $x=1$ is then $$ \begin{array}{lll} \displaystyle \ln x&=\displaystyle \sum_{n=0}^{\infty}\frac{f^{(n)}(1)}{n!}(x-1)^{n}\\ &=\displaystyle \frac{f(1)}{0!}+\frac{f'(1)}{1!}(x-1)+\frac{f''(1)}{2!}(x-1)^2+\frac{f'''(1)}{3!}(x-1)^3+\frac{f^{(4)}(1)}{4!}(x-1)^4+\frac{f^{(5)}(1)}{5!}(x-1)^5+\cdots&\\ &=\displaystyle \frac{0}{1}+\frac{0!}{1!}(x-1)-\frac{1!}{2!}(x-1)^2+\frac{2!}{3!}(x-1)^3-\frac{3!}{4!}(x-1)^4+\frac{4!}{5!}(x-1)^5-\cdots&\\ &=\displaystyle (x-1)-\frac{1}{2}(x-1)^2+\frac{1}{3}(x-1)^3-\frac{1}{4}(x-1)^4+\frac{1}{5}(x-1)^5-\cdots&\\ &=\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}(x-1)^{n}&\\ \end{array} $$ To determine the radius of convergence, $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$ $$ \begin{array}{lll} \displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right| &=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{(-1)^{n+2}}{n+1}(x-1)^{n+1}}{\frac{(-1)^{n+1}}{n}(x-1)^{n}}\right| &\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{n}{n+1}(x-1)\right| &\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\frac{n}{n+1}\left|x-1\right| &\mbox{}\\ &=\displaystyle \left|x-1\right|\lim_{n \rightarrow \infty}\frac{n}{n+1} &\mbox{}\\ &=\displaystyle \left|x-1\right| &\mbox{}\\ &\lt \displaystyle 1 &\mbox{}\\ \end{array} $$ Thus, the series converges absolutely when $|x-1|\lt 1,$ and the radius of convergence is $R=1.$
The series converges absolutely on $(0,2).$
Example: The function $\displaystyle f(x)=\ln x$ can be represented by the power series $\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}(x-1)^{n}.$
Remainder Estimation Theorem for Taylor and Maclaurin Polynomials
Let $f$ be a function that can be differentiated $N + 1$ times on an interval $I$ containing the real number $a.$ Let $p_N$ be the $N$th Taylor polynomial of $f$ at $a$ and let $R_N(x) = f (x) − p_N(x)$ be the $N$th remainder.
If there exists a real number $M$ such that $\displaystyle \left|f^{(N+1)}(x)\right| \leq M$ for all $x$ in $I,$ then $$\displaystyle |R_N(x)| \leq \frac{M}{(N+1)!}|x-a|^{N+1}$$ for all $x$ in $I.$
Example: Remainder Estimation Theorem for Taylor and Maclaurin Polynomials
Find the first and second Taylor polynomials for $f (x) = \sqrt{x}$ at $x = 4.$ Use these polynomials to estimate $\sqrt{6}.$
Noting that $\displaystyle f'(x)=\frac{1}{2\sqrt{x}},$ the first Taylor polynomial is
$$
\begin{array}{lll}
\displaystyle p_1(x)
&=\displaystyle \frac{f(4)}{0!}+\frac{f'(4)}{1!}(x-4)&\\
&=\displaystyle \frac{\sqrt{4}}{1}+\frac{\frac{1}{2\sqrt{4}}}{1!}(x-4)&\\
&=\displaystyle 2+\frac{1}{4}(x-4)&\\
\end{array}
$$
Then, $\displaystyle \sqrt{6}\approx 2+\frac{1}{4}(6-4)=2+\frac{1}{2}=2.5$
Noting that $\displaystyle f''(x)=-\frac{1}{4(\sqrt{x})^3},$ the second Taylor polynomial is $$ \begin{array}{lll} \displaystyle p_2(x) &=\displaystyle \frac{f(4)}{0!}+\frac{f'(4)}{1!}(x-4)+\frac{f''(4)}{2!}(x-4)^2&\\ &=\displaystyle \frac{\sqrt{4}}{1}+\frac{\frac{1}{2\sqrt{4}}}{1}(x-4)+\frac{-\frac{1}{4(\sqrt{4})^3}}{2}(x-4)^2&\\ &=\displaystyle 2+\frac{1}{4}(x-4)-\frac{1}{64}(x-4)^2&\\ \end{array} $$ Then, $\displaystyle \sqrt{6} \approx 2+\frac{1}{4}(6-4)-\frac{1}{64}(6-4)^2=2+\frac{1}{2}-\frac{1}{16}=2.4375.$
Noting that $\displaystyle f''(x)=-\frac{1}{4(\sqrt{x})^3},$ the second Taylor polynomial is $$ \begin{array}{lll} \displaystyle p_2(x) &=\displaystyle \frac{f(4)}{0!}+\frac{f'(4)}{1!}(x-4)+\frac{f''(4)}{2!}(x-4)^2&\\ &=\displaystyle \frac{\sqrt{4}}{1}+\frac{\frac{1}{2\sqrt{4}}}{1}(x-4)+\frac{-\frac{1}{4(\sqrt{4})^3}}{2}(x-4)^2&\\ &=\displaystyle 2+\frac{1}{4}(x-4)-\frac{1}{64}(x-4)^2&\\ \end{array} $$ Then, $\displaystyle \sqrt{6} \approx 2+\frac{1}{4}(6-4)-\frac{1}{64}(6-4)^2=2+\frac{1}{2}-\frac{1}{16}=2.4375.$
Use the Remainder Estimations Theorem to bound the error on the above approximations to $\sqrt{6}.$
Error of $1\mbox{st}$ Approximation: To use the Remainder Estimation Theorem on our approximation using the $1\mbox{st}$ Taylor polynomial,
we need a bound on the magnitude of the $2\mbox{nd}$ derivative of $f(x)=\sqrt{x}.$
It's fairly clear that $\displaystyle |f''(x)|=\frac{1}{4(\sqrt{x})^3}$ is a decreasing function.
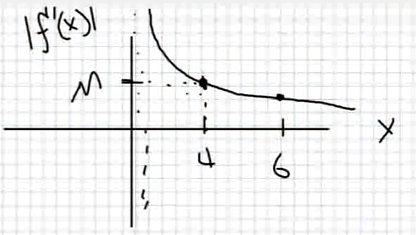
Taking our interval $I$ to be $[4,6],$ we see that $|f''(x)|$ takes its maximum at $x=4.$ That is, $M=\displaystyle \frac{1}{4(\sqrt{4})^3}=\frac{1}{32}.$
We may now bound the error. On the interval $I=[4,6],$ $$ \begin{array}{lll} \displaystyle |R_1(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{\frac{1}{32}}{(1+1)!}|x-4|^{1+1} &\mbox{}\\ &=\displaystyle \frac{1}{32}\cdot\frac{1}{2!}|x-4|^{2} &\mbox{}\\ &=\displaystyle \frac{1}{64}|x-4|^{2} &\mbox{}\\ \end{array} $$ Thus, at $x=6$ $$|R_1(6)| \leq \frac{1}{128}|6-4|^{2}=\frac{4}{62}=\frac{1}{16}=0.0625$$ The error of our approximation is no greater than $0.0625.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $2.5,$ we see that $$ |R_1(6)|=|\sqrt{6}-2.5|=0.05051025722...\lt 0.0625 $$ Error of $2\mbox{nd}$ Approximation: To use the Remainder Estimation Theorem on our approximation using the $2\mbox{nd}$ Taylor polynomial, we need a bound on the magnitude of the $3\mbox{rd}$ derivative of $f(x)=\sqrt{x}.$
It's fairly clear that $\displaystyle |f'''(x)|=\frac{3}{8(\sqrt{x})^5}$ is a decreasing function.

Again, taking our interval $I$ to be $[4,6],$ we see that $|f'''(x)|$ takes its maximum at $x=4.$ That is, $M=\displaystyle \frac{3}{(8\sqrt{4})^5}=\frac{3}{256}.$
We may now bound the error. On the interval $I=[4,6],$ $$ \begin{array}{lll} \displaystyle |R_2(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{\frac{3}{256}}{(2+1)!}|x-4|^{2+1} &\mbox{}\\ &=\displaystyle \frac{3}{256}\cdot\frac{1}{3!}|x-4|^{3} &\mbox{}\\ &=\displaystyle \frac{1}{512}|x-4|^{3} &\mbox{}\\ \end{array} $$ Thus, at $x=6$ $$|R_2(6)| \leq \frac{1}{512}|6-4|^{3}=\frac{8}{512}=\frac{1}{64}=0.015625$$ The error of our approximation is no greater than $0.015625.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $2.4375,$ we see that $$ |R_2(6)|=|\sqrt{6}-2.4375|=0.01198974278...\lt 0.015625 $$
It's fairly clear that $\displaystyle |f''(x)|=\frac{1}{4(\sqrt{x})^3}$ is a decreasing function.

Taking our interval $I$ to be $[4,6],$ we see that $|f''(x)|$ takes its maximum at $x=4.$ That is, $M=\displaystyle \frac{1}{4(\sqrt{4})^3}=\frac{1}{32}.$
We may now bound the error. On the interval $I=[4,6],$ $$ \begin{array}{lll} \displaystyle |R_1(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{\frac{1}{32}}{(1+1)!}|x-4|^{1+1} &\mbox{}\\ &=\displaystyle \frac{1}{32}\cdot\frac{1}{2!}|x-4|^{2} &\mbox{}\\ &=\displaystyle \frac{1}{64}|x-4|^{2} &\mbox{}\\ \end{array} $$ Thus, at $x=6$ $$|R_1(6)| \leq \frac{1}{128}|6-4|^{2}=\frac{4}{62}=\frac{1}{16}=0.0625$$ The error of our approximation is no greater than $0.0625.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $2.5,$ we see that $$ |R_1(6)|=|\sqrt{6}-2.5|=0.05051025722...\lt 0.0625 $$ Error of $2\mbox{nd}$ Approximation: To use the Remainder Estimation Theorem on our approximation using the $2\mbox{nd}$ Taylor polynomial, we need a bound on the magnitude of the $3\mbox{rd}$ derivative of $f(x)=\sqrt{x}.$
It's fairly clear that $\displaystyle |f'''(x)|=\frac{3}{8(\sqrt{x})^5}$ is a decreasing function.

Again, taking our interval $I$ to be $[4,6],$ we see that $|f'''(x)|$ takes its maximum at $x=4.$ That is, $M=\displaystyle \frac{3}{(8\sqrt{4})^5}=\frac{3}{256}.$
We may now bound the error. On the interval $I=[4,6],$ $$ \begin{array}{lll} \displaystyle |R_2(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{\frac{3}{256}}{(2+1)!}|x-4|^{2+1} &\mbox{}\\ &=\displaystyle \frac{3}{256}\cdot\frac{1}{3!}|x-4|^{3} &\mbox{}\\ &=\displaystyle \frac{1}{512}|x-4|^{3} &\mbox{}\\ \end{array} $$ Thus, at $x=6$ $$|R_2(6)| \leq \frac{1}{512}|6-4|^{3}=\frac{8}{512}=\frac{1}{64}=0.015625$$ The error of our approximation is no greater than $0.015625.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $2.4375,$ we see that $$ |R_2(6)|=|\sqrt{6}-2.4375|=0.01198974278...\lt 0.015625 $$
Example: Remainder Estimation Theorem for Taylor and Maclaurin Polynomials
Use the seventh Maclaurin polynomial for $\sin x$ to approximate $\displaystyle \sin\left(1\right)$ and bound the error.
The seventh Maclaurin polynomial for $\sin x$ is
$$p_7(x)=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7$$
Thus,
$$
\sin(1)\approx 1-\frac{1}{3!}1^3+\frac{1}{5!}1^5-\frac{1}{7!}1^7=\frac{4241}{5040}=0.841468254...
$$
Since the largest any of the derivatives of $\sin x$ can be is $1,$ $\displaystyle \left|\frac{d^8}{dx^8}\sin x\right|\leq 1.$
Thus, $M=1$ no matter what interval $I$ we choose. We now have everything we need to bound the error of our approximation.
$$ \begin{array}{lll} \displaystyle |R_7(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{1}{(7+1)!}|x-0|^{7+1} &\mbox{}\\ &=\displaystyle \frac{1}{8!}|x|^{8} &\mbox{}\\ \end{array} $$ Thus, at $x=1$ $$|R_7(1)| \leq \frac{1}{8!}|1|^{8}=\frac{1}{8!}=0.0000248015873$$ The error of our approximation is no greater than $0.0000248015873.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $\displaystyle \frac{4241}{5040}=0.841468254...,$ we see that $$ |R_7(1)|=\left|\sin(1)-\frac{4241}{5040}\right|=0.00000273083964...\lt 0.0000248015873 $$
Thus, $M=1$ no matter what interval $I$ we choose. We now have everything we need to bound the error of our approximation.
$$ \begin{array}{lll} \displaystyle |R_7(x)| &\leq \displaystyle \frac{M}{(N+1)!}|x-a|^{N+1} \\ &=\displaystyle \frac{1}{(7+1)!}|x-0|^{7+1} &\mbox{}\\ &=\displaystyle \frac{1}{8!}|x|^{8} &\mbox{}\\ \end{array} $$ Thus, at $x=1$ $$|R_7(1)| \leq \frac{1}{8!}|1|^{8}=\frac{1}{8!}=0.0000248015873$$ The error of our approximation is no greater than $0.0000248015873.$
Using a calculator we can verify this. Comparing $\sqrt{6}$ to our estimate $\displaystyle \frac{4241}{5040}=0.841468254...,$ we see that $$ |R_7(1)|=\left|\sin(1)-\frac{4241}{5040}\right|=0.00000273083964...\lt 0.0000248015873 $$
For what values of $x$ does the seventh Maclaurin polynomial approximate $\sin x$ to within $0.0001?$
For any value of $x,$ the error bound on the seventh Maclaurin polynomial for $\sin x$ is
$$
\displaystyle |R_7(x)|\leq \frac{1}{8!}|x|^{8}
$$
Thus, if we want to know the values of $x$ for which the seventh Maclaurin polynomial approximates $\sin x$ to within $0.0001,$
that is, $|R_7(x)|\leq 0.0001,$ we solve the inequality
$$
\frac{1}{8!}|x|^{8}\leq 0.0001
$$
Solving for $|x|$ we have
$$
|x|\leq \sqrt[8]{\frac{8!}{10000}}=\sqrt[8]{\frac{40320}{10000}}=\sqrt[8]{4.0320}
$$
Then, the seventh Maclaurin polynomial approximates $\sin x$ to within $0.0001$ on the interval
$$
-\sqrt[8]{4.0320}\leq x \leq \sqrt[8]{4.0320}
$$
or,
$$
-1.190392181...\leq x \leq 1.190392181...
$$

Some Common Series Representations
$\displaystyle \frac{1}{1-x} =\sum_{n=1}^{\infty}x^{n}$ on $(-1,1)$
$\displaystyle \sin x=\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{(2n+1)!}$ on $(-\infty,\infty)$
$\displaystyle \cos x=\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{(2n)!}$ on $(-\infty,\infty)$
$\displaystyle e^x=\sum_{n=0}^{\infty}\frac{x^{n}}{n!}$ on $(-\infty,\infty)$
$\displaystyle \ln x =\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}(x-1)^{n}$ on $(0,2]$
$\displaystyle \sinh x=\sum_{n=0}^{\infty}\frac{x^{2n+1}}{(2n+1)!}$ on $(-\infty,\infty)$
$\displaystyle \cosh x=\sum_{n=0}^{\infty}\frac{x^{2n}}{(2n)!}$ on $(-\infty,\infty)$
$\displaystyle \tan^{-1} x=\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{2n+1}$ on $[-1,1]$