Polynomials (expressions of the form $\displaystyle \sum_{n=0}^{N}c_nx^n$) are a very pliable and handy tool for creating models that describe many different kinds of phenomena.
Today we begin with power series which are expressions of the form $\displaystyle \sum_{n=0}^{\infty}c_nx^n$. As we shall see, power series (infinite polynomials) will enable us to look at old things in a new light and will give us analytical tools which allow us to solve problems that previously we couldn't.
A More Formal Introduction
An expression of the form $\displaystyle \sum_{n=0}^{\infty}c_nx^n$ is a power series centered at $x=0.$
An expression of the form $\displaystyle \sum_{n=0}^{\infty}c_n(x-a)^n$ is a power series centered at $x=a.$
Note: Power series are often indexed starting at $n=0$ since it's prettier. The assumption we must make is that $x^0=1$ and $(x-a)^0=1$ even if $x=0$ or $x-a=0.$
A Familiar Example: Geometric Series
We've already seen that $\displaystyle \sum_{n=0}^{\infty}ax^n=\frac{a}{1-x}$ which converges as long as $|x| \lt 1.$
Otherwise, if $|x|\geq 1,$ the series diverges.
Geometric series are power series with $c_n=a$ for all $n.$
Fact About Power Series
The series $\displaystyle \sum_{n=0}^{\infty}c_nx^n$ won't necessarily converge for all $x$ as our familiar example above has already taught us.
Understanding for what values of $x$ a power series converges will be one of our main tasks in this section.
The next theorem sheds some light on the above.
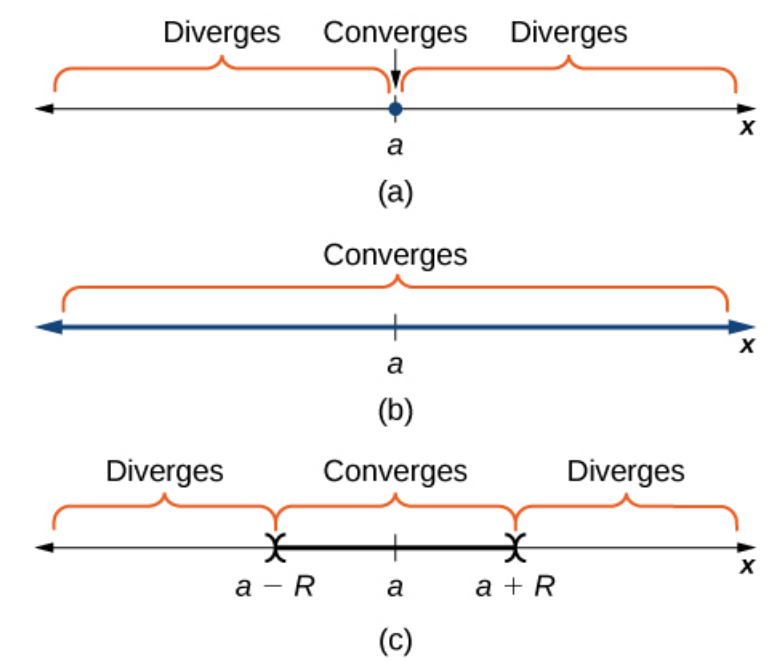
Theorem
For a power series $\displaystyle \sum_{n=0}^{\infty}c_n(x-a)^n,$ exactly one of the following must hold:
(a) The series converges when $x=a$ and diverges when $x \neq a.$
(b) The series converges for all real number values of $x.$
(c) For some number $R \gt 0,$ the series converges whenever $|x-a| \lt R$ and diverges whenever $|x-a| \gt R.$ The series may or may not converge when $|x-a|=R.$
Note: The value of $R$ above is called the radius of convergence. Also in case (a), we say $R=0,$ and in case (b) that $R=\infty.$
Pretty Pictures
Cases (a), (b), and (c) of the above theorem may be visualized as follows.
A Familiar Example: Geometric Series
We've already seen that $\displaystyle \sum_{n=0}^{\infty}ax^n=\frac{a}{1-x}$ which converges as long as $|x| \lt 1.$
Otherwise, if $|x|\geq 1,$ the series diverges.
The radius of convergence $R$ is $1.$ Since the series does not converge at the endpoints $x=-1$ or $x=1,$ the interval of convergence is $(-1,1).$
Question: If given an unfamiliar power series, how do we find the radius and interval of convergence?
Answer: Apply the Ratio Test!
We apply the ratio test to the series $\displaystyle \sum_{n=0}^{\infty}c_n(x-a)^n.$ The series converges absolutely wherever the inequality $$\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right| \lt 1$$ is satisfied. Solving this inequality will give us a statement of the form $|x-a| \lt R.$ The value $R$ is the radius of convergence.
To determine the interval of convergence, we need to decide if the endpoints of the interval result in a convergent series. That is, we need to determine if the series converges at one, both, or none of the $x$ values such that $|x-a|=R.$ (This is the inconclusive case of the Ratio Test.)
The possibilities are $(a-R,a+R),$ $[a-R,a+R),$ $(a-R,a+R],$ and $[a-R,a+R].$
Examples
Determine the radius of convergence and the interval of convergence for the following power series.
$\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^n}{n}$
To determine the radius of convergence $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(-1)^{n}\frac{1}{n+1}x^{n+1}}{(-1)^{n-1}\frac{1}{n} x^n}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(-1)\frac{1}{n+1}x}{\frac{1}{n}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{n}{n+1}x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{n}{n+1}\right| \left| x \right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\frac{n}{n+1}\left| x \right| &\mbox{}\\
&=\displaystyle \left| x \right|\lim_{n \rightarrow \infty}\frac{n}{n+1} &\mbox{}\\
&=\displaystyle \left| x \right| \cdot 1&\mbox{}\\
&=\displaystyle \left| x \right| &\mbox{}\\
&\lt \displaystyle 1 &\mbox{}\\
\end{array}
$$
Thus, the radius of convergence is $R=1$ and the series converges absolutely on $(-1,1).$
To determine the interval of convergence we now test the endpoints of the interval $[-1,1].$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^n}{n} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{(-1)^n}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)^{2n-1}\frac{1}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)^{2n}(-1)\frac{1}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)\frac{1}{n}\\ &=\displaystyle -\sum_{n=1}^{\infty}\frac{1}{n}\\ \end{array} $$ which is a divergent series. (This is just the negative harmonic series). Thus, $-1$ is excluded from the interval of convergence.
At $x=1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^n}{n} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{(1)^n}{n}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{n}\\ \end{array} $$ which is a convergent series by the Alternating Series Test. (The is the alternating harmonic series known to converge to $\ln 2$). Thus, $1$ is included in the interval of convergence.
The interval of convergence is then $(-1,1].$
To determine the interval of convergence we now test the endpoints of the interval $[-1,1].$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^n}{n} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{(-1)^n}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)^{2n-1}\frac{1}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)^{2n}(-1)\frac{1}{n}\\ &=\displaystyle \sum_{n=1}^{\infty}(-1)\frac{1}{n}\\ &=\displaystyle -\sum_{n=1}^{\infty}\frac{1}{n}\\ \end{array} $$ which is a divergent series. (This is just the negative harmonic series). Thus, $-1$ is excluded from the interval of convergence.
At $x=1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^n}{n} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{(1)^n}{n}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{n}\\ \end{array} $$ which is a convergent series by the Alternating Series Test. (The is the alternating harmonic series known to converge to $\ln 2$). Thus, $1$ is included in the interval of convergence.
The interval of convergence is then $(-1,1].$
$\displaystyle \sum_{n=0}^{\infty} \frac{x^n}{n!}$
To determine the radius of convergence $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{\frac{1}{(n+1)!}(x-0)^{n+1}}{\frac{1}{n!} (x-0)^n}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{\frac{1}{(n+1)!}x^{n+1}}{\frac{1}{n!} x^n}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{\frac{1}{(n+1)!}}{\frac{1}{n!} }x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{1}{(n+1)!}\cdot\frac{n!}{1} x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{1}{n+1} x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{1}{n+1}\right| \left| x\right| &\mbox{}\\
&=\displaystyle \left| x\right| \lim_{n \rightarrow \infty} \left|\frac{1}{n+1}\right| &\mbox{}\\
&=\displaystyle |x| \cdot 0 &\mbox{}\\
&\displaystyle \lt 1 &\mbox{}\\
\end{array}
$$
Since the above inequality is satisfied for all $x,$, the radius of convergence is $R=\infty.$
It follows that the interval of convergence is $(-\infty,\infty).$
It follows that the interval of convergence is $(-\infty,\infty).$
$\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(x-2)^n$
To determine the radius of convergence $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{\frac{1}{3^{n+1}}(x-2)^{n+1}}{\frac{1}{3^n}(x-2)^n}\right|&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{\frac{1}{3^{n+1}}(x-2)}{\frac{1}{3^n}}\right|&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{3^n}{3^{n+1}}(x-2)\right|&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{1}{3}(x-2)\right|&\mbox{}\\
&=\displaystyle \left|\frac{1}{3}(x-2)\right|&\mbox{}\\
&=\displaystyle \frac{1}{3}\left|x-2\right|&\mbox{}\\
&\lt \displaystyle 1 &\mbox{}\\
\end{array}
$$
Thus, $|x-2| \lt 3$ so that the radius of convergence is $3.$ Now,
$$
\begin{array}{llll}
&\displaystyle |x-2| \lt 3 &\displaystyle &\mbox{}\\
\implies &\displaystyle -3 \lt x-2 \lt 3&\displaystyle &\mbox{}\\
\implies &\displaystyle -1 \lt x \lt 5&\displaystyle &\mbox{}\\
\end{array}
$$
Thus, the series converges absolutely on $(-1,5).$ To determine the interval of convergence, we now test the endpoints of the interval $[-1,5].$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(x-2)^n &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-1-2)^n\\ &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-3)^n\\ &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-1)^n 3^n\\ &=\displaystyle \sum_{n=0}^{\infty} (-1)^n\\ \end{array} $$ which is a divergent series. Thus, $-1$ is excluded from the interval of convergence.
At $x=5,$ $$ \begin{array}{lll} \displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(x-2)^n &=\displaystyle \sum_{n=1}^{\infty} \frac{1}{3^n}(5-2)^n\\ &=\displaystyle \sum_{n=1}^{\infty} \frac{1}{3^n}3^n\\ &=\displaystyle \sum_{n=1}^{\infty} 1\\ \end{array} $$ which is also a divergent series. Thus, $1$ is also excluded from the interval of convergence.
The interval of convergence is then $(-1,5).$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(x-2)^n &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-1-2)^n\\ &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-3)^n\\ &=\displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(-1)^n 3^n\\ &=\displaystyle \sum_{n=0}^{\infty} (-1)^n\\ \end{array} $$ which is a divergent series. Thus, $-1$ is excluded from the interval of convergence.
At $x=5,$ $$ \begin{array}{lll} \displaystyle \sum_{n=0}^{\infty} \frac{1}{3^n}(x-2)^n &=\displaystyle \sum_{n=1}^{\infty} \frac{1}{3^n}(5-2)^n\\ &=\displaystyle \sum_{n=1}^{\infty} \frac{1}{3^n}3^n\\ &=\displaystyle \sum_{n=1}^{\infty} 1\\ \end{array} $$ which is also a divergent series. Thus, $1$ is also excluded from the interval of convergence.
The interval of convergence is then $(-1,5).$
$\displaystyle \sum_{n=0}^{\infty} n! x^n$
To determine the radius of convergence $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|&=\displaystyle \lim_{n \rightarrow \infty} \left|\frac{\frac{1}{(n+1)!}(x-0)^{n+1}}{\frac{1}{n!} (x-0)^n}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(n+1)! x^{n+1}}{n! x^n}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \left|(n+1)x\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} (n+1)\left|x\right| &\mbox{}\\
&=\displaystyle \left|x\right| \lim_{n \rightarrow \infty} (n+1) &\mbox{}\\
&\displaystyle \lt 1 &\mbox{}\\
\end{array}
$$
Since $\displaystyle \lim_{n \rightarrow \infty} (n+1)=\infty,$ there is no value of $x$ except $0$ which satisfies the inequality.
Thus, the radius of convergence is $R=0.$
It follows that the interval of convergence is $\{0\}.$
It follows that the interval of convergence is $\{0\}.$
$\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{2n-1}$
To determine the radius of convergence $R,$ we compute $\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|.$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left|\frac{c_{n+1}(x-a)^{n+1}}{c_n (x-a)^n}\right|
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(-1)^{(n+1)-1}\frac{x^{2(n+1)-1}}{2(n+1)-1}}{(-1)^{n-1}\frac{x^{2n-1}}{2n-1}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{(-1)^{n}\frac{x^{2n+1}}{2n+1}}{(-1)^{n-1}\frac{x^{2n-1}}{2n-1}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|-\frac{x^{2n+1}}{2n+1}\cdot \frac{2n-1}{x^{2n-1}}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|\frac{x^2}{2n+1}\cdot \frac{2n-1}{1}\right| &\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left|x^2\right|\left|\frac{2n-1}{2n+1}\right| &\mbox{}\\
&=\displaystyle \left|x^2\right|\lim_{n \rightarrow \infty}\left|\frac{2n-1}{2n+1}\right| &\mbox{}\\
&=\displaystyle \left|x^2\right|\cdot 1 &\mbox{}\\
&=\displaystyle \left|x^2\right| &\mbox{}\\
&=\displaystyle x^2 &\mbox{}\\
&\lt \displaystyle 1 &\mbox{}\\
\end{array}
$$
The above implies that the series converges absolutely when $|x^2|\lt 1,$ which is equivalent to the inequality $|x|\lt 1,$ or, $-1 \lt x \lt 1.$
Thus, the radius of convergence is $R=1.$
To determine the interval of convergence, we now test the endpoints of the interval $[-1,1].$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{2n-1} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}(-1)^{2n}(-1)^{-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}(-1)^{-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-2}\frac{1}{2n-1}\\ \end{array} $$ which is a convergent series by the Alternating Series Test. Thus, $-1$ is included in the interval of convergence.
At $x=1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{2n-1} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1^{2n-1}}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{2n-1}\\ \end{array} $$ which is also a convergent series by the Alternating Series Test. Thus, $1$ is also included in the interval of convergence.
The interval of convergence is then $[-1,1].$
To determine the interval of convergence, we now test the endpoints of the interval $[-1,1].$
At $x=-1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{2n-1} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}(-1)^{2n}(-1)^{-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}(-1)^{-1}\frac{1}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-2}\frac{1}{2n-1}\\ \end{array} $$ which is a convergent series by the Alternating Series Test. Thus, $-1$ is included in the interval of convergence.
At $x=1,$ $$ \begin{array}{lll} \displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{2n-1} &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1^{2n-1}}{2n-1}\\ &=\displaystyle \sum_{n=1}^{\infty} (-1)^{n-1}\frac{1}{2n-1}\\ \end{array} $$ which is also a convergent series by the Alternating Series Test. Thus, $1$ is also included in the interval of convergence.
The interval of convergence is then $[-1,1].$
Representing Functions as Power Series
For every value of $x$ in the interval of convergence of a power series, we get a real number in return. That is to say, a power series is a function whose domain is its interval of convergence.
We will now turn that idea on its ear by asking a question: given some function $f(x),$ can we find a power series that equals $f(x)$ for some or all values of $x$ in the domain of $f?$
This will be a question that we will be able to more fully answer by then end of Section 6.3. However, we will begin to address this question milking familiar series for ideas.
A Familiar Example... Again! Milking the Geometric Series for All It's Worth!
The function $\displaystyle f(x)=\frac{1}{1-x}$ can be represented by the power series $\displaystyle \sum_{n=0}^{\infty}x^n$ on the interval $(-1,1).$
Awesome News!
By the end of Section 6.3, we'll be able to come up with series representations for almost any function we could possibly want! (With some restrictions, course.)
But for now...
Milking Geometric Series Even More...
Use a power series to represent each of the following functions $f.$ Find the interval of convergence.
$\displaystyle f(x)=\frac{1}{1+x^2}$
$$
\begin{array}{lll}
\displaystyle f(x)
&=\displaystyle \frac{1}{1+x^2}&\mbox{}\\
&=\displaystyle \frac{1}{1-(-x^2)}&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}(-x^2)^n&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}(-1)^n x^{2n}&\mbox{}\\
\end{array}
$$
Since the interval of convergence for the series $\displaystyle \sum_{n=0}^{\infty}x^n=\frac{1}{1-x}$ is given by $|x|\lt 1,$
the interval of convergence for $f(x)$ is given by $|-x^2|\lt 1,$ or, $(-1,1).$
$\displaystyle f(x)=\frac{x^2}{4-x^2}$
Our goal is to massage an expression of the form $\displaystyle \frac{1}{1-(\,\,)}$ out of $\displaystyle \frac{x^2}{4-x^2}.$
$$
\begin{array}{lll}
\displaystyle f(x)
&=\displaystyle \frac{x^2}{4-x^2}&\mbox{}\\
&=\displaystyle x^2\frac{1}{4\left(1-\frac{x^2}{4}\right)}&\mbox{}\\
&=\displaystyle \frac{x^2}{4}\frac{1}{1-\frac{x^2}{4}}&\mbox{}\\
&=\displaystyle \frac{x^2}{4}\sum_{n=0}^{\infty}\left(\frac{x^2}{4}\right)^n&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}\left(\frac{x^2}{4}\right)^{n+1}&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}\frac{x^{2(n+1)}}{4^{n+1}}&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}\frac{1}{4^{n+1}}x^{2(n+1)}&\mbox{}\\
&=\displaystyle \sum_{n=1}^{\infty}\frac{1}{4^n}x^{2n}&\mbox{re-indexing the sum}\\
\end{array}
$$
Since the interval of convergence for the series $\displaystyle \sum_{n=0}^{\infty}x^n=\frac{1}{1-x}$ is given by $|x|\lt 1,$
the interval of convergence for $f(x)$ is given by $\displaystyle \left|\frac{x^2}{4}\right|\lt 1.$
Then $$ \begin{array}{llll} &\displaystyle -1 \lt \frac{x^2}{4} \lt 1&\displaystyle &\mbox{}\\ \implies &\displaystyle -4 \lt x^2 \lt 4 &\displaystyle &\mbox{}\\ \implies &\displaystyle x^2 \lt 4 &\displaystyle &\mbox{since $x^2$ is non-negative}\\ \implies &\displaystyle |x| \lt 2 &\displaystyle &\mbox{}\\ \implies &\displaystyle -2 \lt x \lt 2 &\displaystyle &\mbox{}\\ \end{array} $$ Thus, the interval of convergence is $(-2,2).$
Then $$ \begin{array}{llll} &\displaystyle -1 \lt \frac{x^2}{4} \lt 1&\displaystyle &\mbox{}\\ \implies &\displaystyle -4 \lt x^2 \lt 4 &\displaystyle &\mbox{}\\ \implies &\displaystyle x^2 \lt 4 &\displaystyle &\mbox{since $x^2$ is non-negative}\\ \implies &\displaystyle |x| \lt 2 &\displaystyle &\mbox{}\\ \implies &\displaystyle -2 \lt x \lt 2 &\displaystyle &\mbox{}\\ \end{array} $$ Thus, the interval of convergence is $(-2,2).$
$\displaystyle f(x)=\frac{x^3}{2-x}$
$$
\begin{array}{lll}
\displaystyle f(x)
&=\displaystyle \frac{x^3}{2-x}&\mbox{}\\
&=\displaystyle x^3\frac{1}{2\left(1-\frac{x}{2}\right)}&\mbox{}\\
&=\displaystyle \frac{x^3}{2}\frac{1}{1-\frac{x}{2}}&\mbox{}\\
&=\displaystyle \frac{x^3}{2}\sum_{n=0}^{\infty}\left(\frac{x}{2}\right)^n&\mbox{}\\
&=\displaystyle \frac{x^3}{2}\sum_{n=0}^{\infty}\frac{x^n}{2^n}&\mbox{}\\
&=\displaystyle \sum_{n=0}^{\infty}\frac{x^{n+3}}{2^{n+1}}&\mbox{}\\
\end{array}
$$
Since the interval of convergence for the series $\displaystyle \sum_{n=0}^{\infty}x^n=\frac{1}{1-x}$ is given by $|x|\lt 1,$
the interval of convergence for $f(x)$ is given by $\displaystyle \left|\frac{x}{2}\right|\lt 1.$
Then $$ \begin{array}{llll} &\displaystyle -1 \lt \frac{x}{2} \lt 1&\displaystyle &\mbox{}\\ \implies &\displaystyle -2 \lt x \lt 2 &\displaystyle &\mbox{}\\ \end{array} $$ Thus, the interval of convergence is $(-2,2).$
Then $$ \begin{array}{llll} &\displaystyle -1 \lt \frac{x}{2} \lt 1&\displaystyle &\mbox{}\\ \implies &\displaystyle -2 \lt x \lt 2 &\displaystyle &\mbox{}\\ \end{array} $$ Thus, the interval of convergence is $(-2,2).$