A series whose terms alternate between positive and negative value is called an alternating series.
Alternating series appear in MANY applications as we shall later see.
Examples of Alternating Series
$\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots$
$\displaystyle \sum_{n=1}^{\infty}\left(-\frac{1}{2}\right)^n=-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-\frac{1}{32}+\cdots$
$\displaystyle \sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}=1-\frac{1}{2!}+\frac{1}{4!}-\frac{1}{6!}+\frac{1}{8!}-\frac{1}{10!}+\cdots$
The Alternating Harmonic Series: $\displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}$
| Partial Sum $S_N$ | |||
| $N$ |
The Alternating Harmonic Series $$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{n}=\ln 2$$
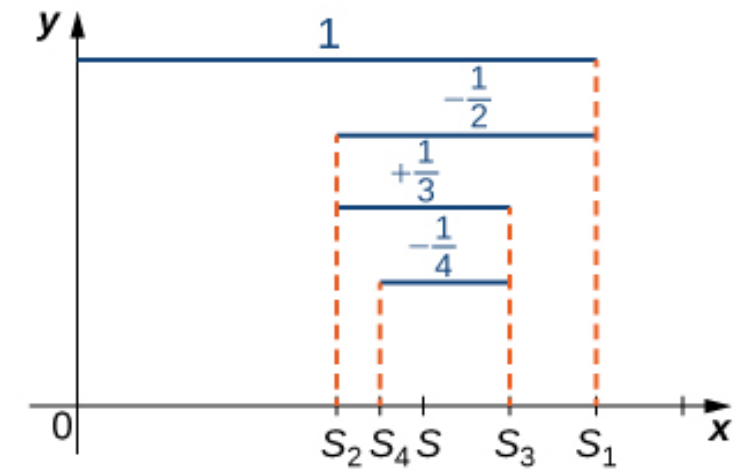
The Alternating Series Test
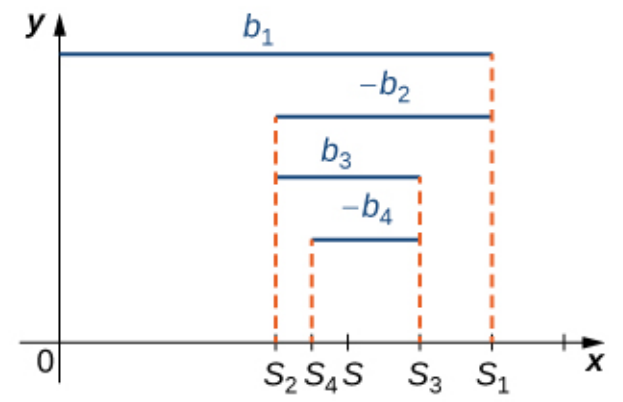
An alternating series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}b_n$ or $\displaystyle \sum_{n=1}^{\infty}(-1)^{n}b_n$ converges if
i. $0 \leq b_{n+1} \leq b_n$ for all $n \geq 1$and
ii. $\displaystyle \lim_{n \rightarrow \infty} b_n=0$
Note: This theorem is true more generally as long as there exists some integer $N$ such that $0 \leq b_{n + 1} \leq b_n$ for all $n \geq N.$
Reasoning of the Alternating Series Test
For an alternating series $b_1 - b_2 + b_3 - b_4+\cdots,$ we move forward a certain distance $b_1,$ then back by a shorter distance $b_2,$ then forward by an even shorter distance $b_3,$ then back again by an even shorter distance $b_4,$...
Continuing the above process indefinitely, we see that we must "settle in" on some location.
Examples: State whether each of the following series converges.
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{\sqrt{n+3}}$
Here, $\displaystyle b_n=\frac{1}{\sqrt{n+3}}$ is decreasing for all $n \geq 1.$ Moreover,
$\displaystyle \lim_{n \rightarrow \infty} b_n=\lim_{n \rightarrow \infty} \frac{1}{\sqrt{n+3}}=0.$
By the Alternating Series Test, the series converges.
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}$
We note that $\displaystyle \lim_{n \rightarrow \infty} (-1)^{n+1}\frac{\sqrt{n}+1}{\sqrt{n}+3}$
does not exist.
Therefore, by the Divergence Test, the series diverges.
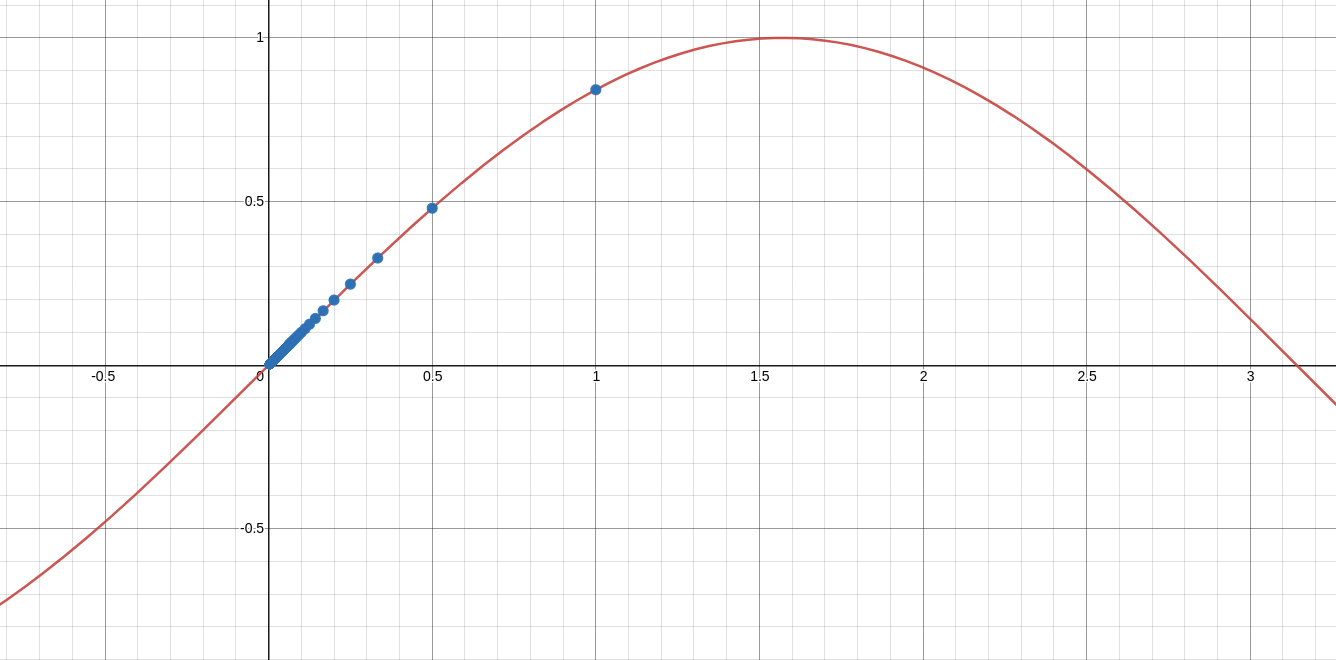
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\sin (1/n)$
Here, $\displaystyle b_n=\sin(1/n)$ is decreasing for all $n \geq 1$ (see figure below).
Moreover,
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} b_n&= \displaystyle \lim_{n \rightarrow \infty} \sin (1/n)&\\
&=\displaystyle \sin(\lim_{n \rightarrow \infty} 1/n)& \mbox{by the Continuous Function Theorem}\\
&=\displaystyle \sin (0)&\\
&=0.&\\
\end{array}
$$
By the Alternating Series Test, the series converges.

$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1}$
Here, $\displaystyle b_n=\frac{1}{n^2+1}$ is decreasing for all $n \geq 1.$ Moreover,
$\displaystyle \lim_{n \rightarrow \infty} b_n=\lim_{n \rightarrow \infty} \frac{1}{n^2+1}=0.$
By the Alternating Series Test, the series converges.
Estimating Sums
Generally speaking, finding exact sums of alternating series can be difficult.
The next best thing to an exact sum is an approximation with a known bound on the _____________.
Remainders in Alternating Series
Suppose $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}b_n$ and $\displaystyle \sum_{n=1}^{\infty}(-1)^{n}b_n$ are series which satisfy the alternating series test. Let $S$ denote the sum of the series and $S_N$ denote the $N$th partial sum.
Then, for any integer $N \geq 1,$ the remainder $R_N = S - S_N$ satisfies $$|R_N| \leq b_{N+1}.$$ This means...
$$S_N-b_{N+1}\leq \sum_{n=1}^{\infty}(-1)^{n+1}b_n \leq S_N+b_{N+1}$$
Example
For the alternating harmonic series, compare the error of $N$th partial sum $\displaystyle |R_N|=\left|\ln 2-\sum_{n=1}^{N} \frac{(-1)^{n+1}}{n}\right|$ with the error bound $\displaystyle |R_N|\leq\frac{1}{b_{N+1}}=\frac{1}{N+1}$
Example
For the series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1},$ use the remainder estimate to determine a bound on the error $R_{10}$ if we approximate the sum of the series by the partial sum $S_{10}.$
Find a value of $N$ that guarantees that the sum of the first $N$ terms differs from the infinite sum by at most $10^{-5}.$
The bound on the error on the error for the $10$th term is $\displaystyle |R_{10}|\leq b_{11}=\frac{1}{11^2+1}=\frac{1}{122}=0.008196721...$
From the above we saw that
$\displaystyle S_N-b_{N+1}\leq \sum_{n=1}^{\infty}(-1)^{n+1}b_n \leq S_N+b_{N+1}.$
For this situation,
$$ S_{10}-b_{11}\leq \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1} \leq S_{10}+b_{11}$$
Calculating the $10$th partial sum, $S_{10}=0.35952049849...,$ and noting that $\displaystyle b_{11}=\frac{1}{122}=0.008196721...$the above becomes
$$ 0.35952049849...-0.00819672131...\leq \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1} \leq 0.35952049849...+0.00819672131...$$
That is,
$$ 0.3513237772...\leq \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1} \leq 0.3677172198...$$
To obtain an error of $10^{-5}$ or less, we know the number of terms, $N,$ must satisfy $$|R_{N}|\leq b_{N+1}=\frac{1}{(N+1)^2+1}\leq 10^{-5}.$$
Then $\displaystyle 10^5 \leq (N+1)^2+1$ so that $N \geq \sqrt{10^5-1}-1=315.2261849...$
Thus, we need at least $316$ terms to approximate the sum with an error of $10^{-5}$ or less.
Thus, we need at least $316$ terms to approximate the sum with an error of $10^{-5}$ or less.
Absolute and Conditional Convergence
Pop Quiz
The harmonic series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n},$ converges/diverges. (circle one).
The alternating harmonic series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n},$ converges/diverges. (circle one).
The series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1},$ converges/diverges. (circle one).
The series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2+1},$ converges/diverges. (circle one).
Absolute and Conditional Convergence
We say that the alternating harmonic series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n}$ converges conditionally since $\displaystyle \sum_{n=1}^{\infty}\left|(-1)^{n+1}\frac{1}{n}\right| =\sum_{n=0}^{\infty}\frac{1}{n}$ diverges.
On the other hand, the series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n^2+1}$ converges absolutely since $\displaystyle \sum_{n=1}^{\infty}\left|(-1)^{n+1}\frac{1}{n^2+1}\right| =\sum_{n=0}^{\infty}\frac{1}{n^2+1}$ converges.
Definition: Absolute and Conditional Convergence
A convergent series $\displaystyle \sum_{n=1}^{\infty}a_n$ is said to converge absolutely if $\displaystyle \sum_{n=0}^{\infty} |a_n|$ also converges.
A convergent series $\displaystyle \sum_{n=1}^{\infty}a_n$ is said to converge conditionally if $\displaystyle \sum_{n=0}^{\infty} |a_n|$ diverges.
Theorem: Absolute Convergence Implies Convergence
If $\displaystyle \sum_{n=1}^{\infty}|a_n|$ converges then
$\displaystyle \sum_{n=0}^{\infty} a_n$ also converges.
We shall label this theorem the $\mbox{ACIC}$ Theorem for short.
Examples: For each of the following series, determine whether the series converges absolutely, converges conditionally, or diverges.
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{\sqrt{n+3}}$
Earlier we established by the Alternating Series Test that $\displaystyle \sum_{n=1}^{\infty}a_n =\sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{\sqrt{n+3}}$
is a convergent series. However, we see that the series $\displaystyle \sum_{n=1}^{\infty}|a_n|= \sum_{n=1}^{\infty}\frac{1}{\sqrt{n+3}}$
is divergent by the Limit Comparison Test using the harmonic series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ for comparison.
Thus, the series is conditionally convergent.
Thus, the series is conditionally convergent.
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1}\sin (1/n)$
Earlier we established by the Alternating Series Test that $\displaystyle \sum_{n=1}^{\infty}a_n =\sum_{n=1}^{\infty}(-1)^{n+1} \sin (1/n)$
is a convergent series.
However, comparing the series $\displaystyle \sum_{n=1}^{\infty}|a_n|= \sum_{n=1}^{\infty}\sin (1/n)$ with the harmonic series $\displaystyle \sum_{n=1}^{\infty}b_n=\sum_{n=1}^{\infty}\frac{1}{n}$ using the Limit Comparison Test, $$ \begin{array}{lll} \displaystyle \lim_{n \rightarrow \infty}\frac{|a_n|}{b_n}&=\displaystyle \lim_{n \rightarrow \infty}\frac{\sin (1/n)}{1/n}&\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\frac{\cos (1/n)\cdot(-1/n^2)}{-1/n^2}&\mbox{using L'Hopital}\\ &=\displaystyle \lim_{n \rightarrow \infty}\cos (1/n)&\mbox{}\\ &=\displaystyle \cos (\lim_{n \rightarrow \infty} 1/n)&\mbox{by the Continuous Function Theorem}\\ &=\displaystyle \cos (0)&\mbox{}\\ &=\displaystyle 1&\mbox{}\\ \end{array} $$ we see that $\displaystyle \sum_{n=1}^{\infty}|a_n|= \sum_{n=1}^{\infty}\sin (1/n)$ is divergent.
Thus, the series is conditionally convergent.
However, comparing the series $\displaystyle \sum_{n=1}^{\infty}|a_n|= \sum_{n=1}^{\infty}\sin (1/n)$ with the harmonic series $\displaystyle \sum_{n=1}^{\infty}b_n=\sum_{n=1}^{\infty}\frac{1}{n}$ using the Limit Comparison Test, $$ \begin{array}{lll} \displaystyle \lim_{n \rightarrow \infty}\frac{|a_n|}{b_n}&=\displaystyle \lim_{n \rightarrow \infty}\frac{\sin (1/n)}{1/n}&\mbox{}\\ &=\displaystyle \lim_{n \rightarrow \infty}\frac{\cos (1/n)\cdot(-1/n^2)}{-1/n^2}&\mbox{using L'Hopital}\\ &=\displaystyle \lim_{n \rightarrow \infty}\cos (1/n)&\mbox{}\\ &=\displaystyle \cos (\lim_{n \rightarrow \infty} 1/n)&\mbox{by the Continuous Function Theorem}\\ &=\displaystyle \cos (0)&\mbox{}\\ &=\displaystyle 1&\mbox{}\\ \end{array} $$ we see that $\displaystyle \sum_{n=1}^{\infty}|a_n|= \sum_{n=1}^{\infty}\sin (1/n)$ is divergent.
Thus, the series is conditionally convergent.
$\displaystyle \sum_{n=1}^{\infty}\frac{(-2)^{n}}{n+3^n}$
We see that $\displaystyle |a_n|=\frac{2^{n}}{n+3^n}\leq \frac{2^n}{3^n}=\left(\frac{2}{3}\right)^n.$ Thus, by direct comparison with the geometric series
$\displaystyle \sum_{n=1}^{\infty}\left(\frac{2}{3}\right)^n,$
the series $\displaystyle \sum_{n=1}^{\infty}|a_n| = \sum_{n=1}^{\infty}\frac{2^n}{n+3^n}$ converges.
Thus, by the $\mbox{ACIC}$ Theorem, the alternating series $\displaystyle \sum_{n=1}^{\infty}\frac{(-2)^{n}}{n+3^n}$ converges absolutlely.
Thus, by the $\mbox{ACIC}$ Theorem, the alternating series $\displaystyle \sum_{n=1}^{\infty}\frac{(-2)^{n}}{n+3^n}$ converges absolutlely.
$\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{\ln(n)}{n^2}$
We first consider the series $\displaystyle \sum_{n=1}^{\infty}|a_n|=\sum_{n=1}^{\infty}\frac{\ln(n)}{n^2}.$
Trying multiple inconclusive comparisons, we see that the Comparison Tests might not be the best method to test
Therefore, we shall invoke the Integral Test. In a previous example from last term established that $\displaystyle \int_{1}^{\infty} \frac{\ln x}{x^2} \, dx=1.$ Since this integral converges, we have by the Integral Test that $\displaystyle \sum_{n=1}^{\infty}|a_n|=\sum_{n=1}^{\infty}\frac{\ln(n)}{n^2}$ converges.
Thus, by the $\mbox{ACIC}$ Theorem, the alternating series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{\ln(n)}{n^2}$ converges absolutely.
Trying multiple inconclusive comparisons, we see that the Comparison Tests might not be the best method to test
Therefore, we shall invoke the Integral Test. In a previous example from last term established that $\displaystyle \int_{1}^{\infty} \frac{\ln x}{x^2} \, dx=1.$ Since this integral converges, we have by the Integral Test that $\displaystyle \sum_{n=1}^{\infty}|a_n|=\sum_{n=1}^{\infty}\frac{\ln(n)}{n^2}$ converges.
Thus, by the $\mbox{ACIC}$ Theorem, the alternating series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{\ln(n)}{n^2}$ converges absolutely.
Alternating $p$-Series $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{n^p}$
If $0 \lt p \leq 1,$ the alternating $p$-series converges conditionally.
If $p \gt 1,$ the alternating $p$-series converges absolutely.
Example: $\displaystyle \displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{\sqrt{n}}=\sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{n^{1/2}}$
converges conditionally.
If $p \gt 1,$ the alternating $p$-series converges absolutely.
Example: $\displaystyle \sum_{n=1}^{\infty}(-1)^{n+1} \frac{1}{n^3}$ converges absolutely.