In the last section we were introduced to infinite series.
We saw that a series may either converge or diverge, but making that determination could be difficult.
Moreover, when a series converges, can we determine its value?
In this section we begin tackling some of these questions.
A Test for Divergence
We shall now show that if a series $\displaystyle \sum_{n=1}^{\infty}a_n$ converges, then it must be that $\displaystyle \lim_{n \rightarrow \infty} a_n=0.$
Let $\varepsilon \gt 0.$
Since $\displaystyle \sum_{n=1}^{\infty}a_n$ converges, we can suppose that the sequence of partial sums, $\displaystyle S_N=\sum_{n=1}^{N}a_n,$ converges to some limit $L.$
Then we can find an $N$ such that $$ \displaystyle \left|S_N-L\right|=\left| \sum_{n=1}^{N}a_n-L \right| \lt \frac{\varepsilon}{2} $$ This also means $$ \displaystyle \left|S_{N+1}-L\right|=\left| \sum_{n=1}^{N+1}a_n-L \right| \lt \frac{\varepsilon}{2} $$ Restating the above into inequalities without absolute values, we have $$ -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N}a_n-L\lt \frac{\varepsilon}{2} \mbox{ and } -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N+1}a_n-L\lt \frac{\varepsilon}{2} $$ Multiplying the the above inequality on the left by $-1$ and rearranging, we get $$ -\lt \frac{\varepsilon}{2} \lt -\sum_{n=1}^{N}a_n+L\lt \frac{\varepsilon}{2} \mbox{ and } -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N+1}a_n-L\lt \frac{\varepsilon}{2} $$ Adding the left and right inequalities above we get $$ -\varepsilon \lt a_{N+1} \lt \varepsilon $$ or, $|a_{N+1}-0|\lt \varepsilon$ Thus, we have shown that $$ \lim_{n \rightarrow \infty} a_n=0 $$ $\square$
Since $\displaystyle \sum_{n=1}^{\infty}a_n$ converges, we can suppose that the sequence of partial sums, $\displaystyle S_N=\sum_{n=1}^{N}a_n,$ converges to some limit $L.$
Then we can find an $N$ such that $$ \displaystyle \left|S_N-L\right|=\left| \sum_{n=1}^{N}a_n-L \right| \lt \frac{\varepsilon}{2} $$ This also means $$ \displaystyle \left|S_{N+1}-L\right|=\left| \sum_{n=1}^{N+1}a_n-L \right| \lt \frac{\varepsilon}{2} $$ Restating the above into inequalities without absolute values, we have $$ -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N}a_n-L\lt \frac{\varepsilon}{2} \mbox{ and } -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N+1}a_n-L\lt \frac{\varepsilon}{2} $$ Multiplying the the above inequality on the left by $-1$ and rearranging, we get $$ -\lt \frac{\varepsilon}{2} \lt -\sum_{n=1}^{N}a_n+L\lt \frac{\varepsilon}{2} \mbox{ and } -\lt \frac{\varepsilon}{2} \lt \sum_{n=1}^{N+1}a_n-L\lt \frac{\varepsilon}{2} $$ Adding the left and right inequalities above we get $$ -\varepsilon \lt a_{N+1} \lt \varepsilon $$ or, $|a_{N+1}-0|\lt \varepsilon$ Thus, we have shown that $$ \lim_{n \rightarrow \infty} a_n=0 $$ $\square$
The contrapositive of the above result gives us...
The Divergence Test
If $\displaystyle \lim_{n \rightarrow \infty} a_n \neq 0,$ then $\displaystyle \sum_{n=1}^{\infty}a_n$ diverges.
If $\displaystyle \lim_{n \rightarrow \infty} a_n = 0,$ then we cannot say if $\displaystyle \sum_{n=1}^{\infty}a_n$ diverges or not.
Examples
$\displaystyle \sum_{n=1}^{\infty} n^2$
Since $\displaystyle \lim_{n \rightarrow \infty} a_n=\lim_{n \rightarrow \infty} n^2=\infty \neq 0,$
we conclude by the Divergence Test that the series diverges.
$\displaystyle \sum_{n=1}^{\infty} \frac{n+1}{n}$
Since $\displaystyle \lim_{n \rightarrow \infty} a_n=\lim_{n \rightarrow \infty} \frac{n+1}{n}=1 \neq 0,$
we conclude by the Divergence Test that the series diverges.
$\displaystyle \sum_{n=1}^{\infty} (-1)^{n+1}$
Since $\displaystyle \lim_{n \rightarrow \infty} a_n=\lim_{n \rightarrow \infty} (-1)^{n+1}$ does not exist (cannot equal $0$),
we conclude by the Divergence Test that the series diverges.
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n}$
$\displaystyle \lim_{n \rightarrow \infty} a_n=\lim_{n \rightarrow \infty} \frac{1}{n}= 0.$ The Divergence Test is inconclusive.
Dire Warning #1
$\displaystyle \lim_{n \rightarrow \infty} a_n = 0$ DOES NOT imply that
$\displaystyle \sum_{n=1}^{\infty}a_n$ converges!!!!!!!!!!!!!!!!!!


Recall: Although $\displaystyle \lim_{n \rightarrow \infty} \frac{1}{n}=0,$ the Harmonic Series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ still diverges.
| Partial Sum $S_N$ | |||
| $N$ |
Interesting Facts About the Harmonic Series
The Harmonic Series is diverges very slowly. In fact, $\displaystyle \sum_{n=1}^{178,000,000}\frac{1}{n} \lt 20.$
That is, we must add more than $178$ million terms for the partial sum $\displaystyle \sum_{n=1}^{N}\frac{1}{n}$ to crack $20.$ (Wow!)
Moreover, recall from last time that we must add more than $10^{43}$ terms to reach $100.$ (Wow!!!)
Yet, by taking sufficiently many terms ($N$ sufficiently large), we can make $\displaystyle \sum_{n=1}^{N}\frac{1}{n}$ as large as we like.
Question: If Is there an easier way to show that a series diverges?
The Integral Test
Let $\displaystyle \sum_{n=1}^{\infty}a_n$ be a series with positive terms $a_n.$ Suppose there exists a function $f$ and a positive integer $N$ such that the following three conditions are satisfied:
$f$ is continuous
$f$ is decreasing
$f(n)=a_n$ for all $n \geq N.$
Then $\displaystyle \sum_{n=1}^{\infty}a_n$ and $\displaystyle \int_{N}^{\infty}f(x) \, dx$ either both converge or both diverge.
Comparing $\displaystyle \sum_{n=1}^{\infty}a_n$ and $\displaystyle \int_{N}^{\infty}f(x) \, dx$
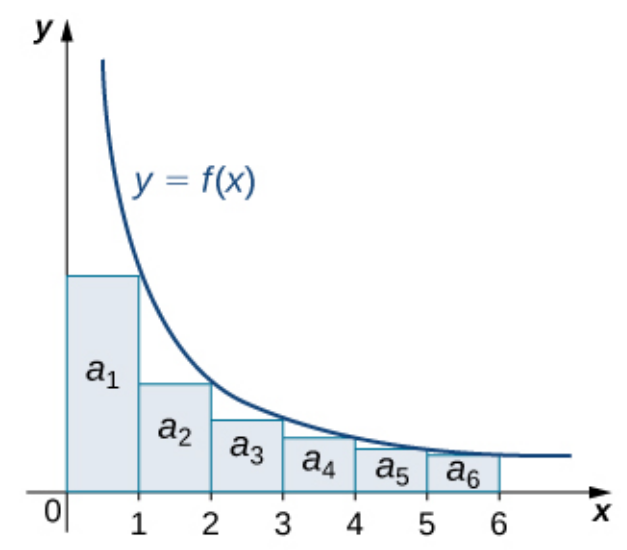 | 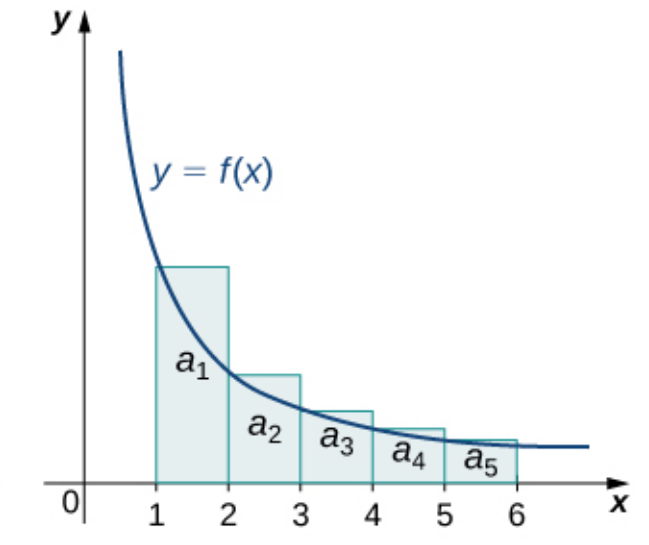 |
| $\displaystyle \sum_{n=1}^{\infty}a_n \lt \displaystyle \int_{0}^{\infty}f(x) \, dx$ | $\displaystyle \sum_{n=1}^{\infty}a_n \gt \displaystyle \int_{1}^{\infty}f(x) \, dx$ |
| integral converges $\Rightarrow$ series converges | integral diverges $\Rightarrow$ series diverges |
Examples: Use the integral test to show the following:
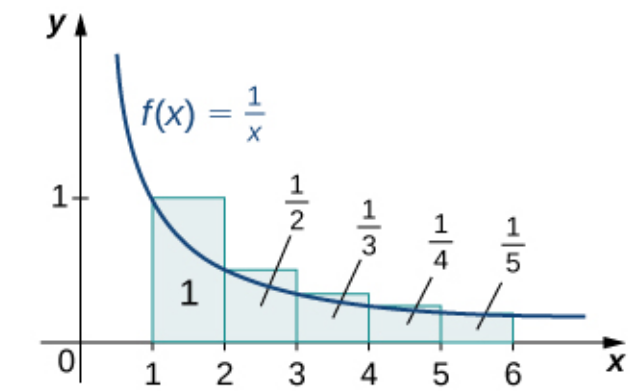 | 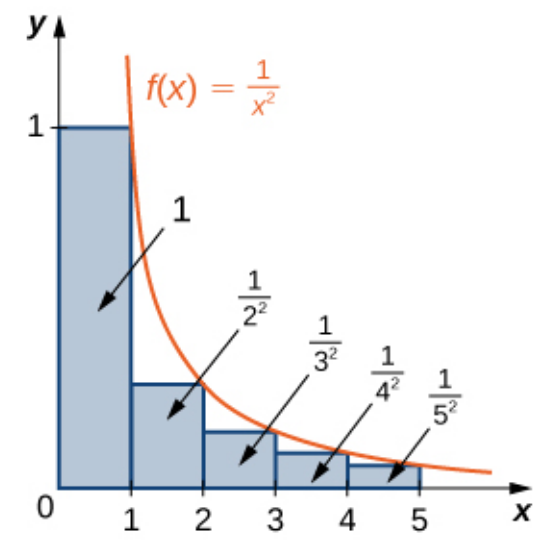 |
| $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ | $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ |
| diverges. | converges. |
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ Diverges
First we note that $\displaystyle f(x)=\frac{1}{x}$ is continuous and decreasing on the interval $[1,\infty).$
Moreover, $\displaystyle f(n)=\frac{1}{n}=a_n$ for all $n \geq 1.$
Therefore, by the integral test, the harmonic series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ diverges since $\displaystyle \int_{1}^{\infty}\frac{1}{x} \,dx$ diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ Converges
First we note that $\displaystyle f(x)=\frac{1}{x^2}$ is continuous and decreasing on the interval $[1,\infty).$
Moreover, $\displaystyle f(n)=\frac{1}{n^2}=a_n$ for all $n \geq 1.$
Therefore, by the integral test, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ converges since $\displaystyle \int_{1}^{\infty}\frac{1}{x^2} \,dx$ converges.
First we note that $\displaystyle f(x)=\frac{1}{x}$ is continuous and decreasing on the interval $[1,\infty).$
Moreover, $\displaystyle f(n)=\frac{1}{n}=a_n$ for all $n \geq 1.$
Therefore, by the integral test, the harmonic series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$ diverges since $\displaystyle \int_{1}^{\infty}\frac{1}{x} \,dx$ diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ Converges
First we note that $\displaystyle f(x)=\frac{1}{x^2}$ is continuous and decreasing on the interval $[1,\infty).$
Moreover, $\displaystyle f(n)=\frac{1}{n^2}=a_n$ for all $n \geq 1.$
Therefore, by the integral test, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ converges since $\displaystyle \int_{1}^{\infty}\frac{1}{x^2} \,dx$ converges.
More Examples: Use the Integral Test to decide if the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^3}$
Since $\displaystyle \int_{1}^{\infty}\frac{1}{x^3}\,dx$ converges, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^3}$ converges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{\sqrt{3n-2}}$
Since $\displaystyle \int_{1}^{\infty}\frac{1}{\sqrt{3x-2}}\,dx$ diverges, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{\sqrt{3n-2}}$ diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2+1}$
Since $\displaystyle \int_{1}^{\infty}\frac{1}{x^2+1}\,dx$ converges, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2+1}$ converges.
Example: Use the Integral Test to decide:
For which values of $p$ does the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converge?
For which values of $p$ does the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ diverge?
Note: A series of the form $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ is called a $p$-series.
For any $p>0$ we note that the integral Integral Test applies to the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ since
$\displaystyle f(x)=\frac{1}{x^p}$ is continuous and decreasing on the interval $[1,\infty)$
and $\displaystyle f(n)=\frac{1}{n^p}=a_n$ for all $n \geq 1.$
Recalling the result we derived in Section $3.7$ concerning improper integrals of the form $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$
If $p \gt 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ converges.
If $p \leq 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ diverges.
The Integral Test then tells us that $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converges when $p \gt 1$ an diverges when $0 \lt p \leq 1.$
For $p<0,$ we see that $\displaystyle \lim_{n \rightarrow \infty}a_n=\lim_{n \rightarrow \infty}\frac{1}{x^p}=\infty\neq 0.$
Thus, by the Divergence Test, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ diverges if $p \lt 0.$
In Summary
If $p \gt 1,$ then $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converges.
If $p \leq 1,$ then $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ diverges.
Recalling the result we derived in Section $3.7$ concerning improper integrals of the form $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$
If $p \gt 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ converges.
If $p \leq 1,$ then $\displaystyle \int_{1}^{\infty} \frac{1}{x^p} \, dx$ diverges.
The Integral Test then tells us that $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converges when $p \gt 1$ an diverges when $0 \lt p \leq 1.$
For $p<0,$ we see that $\displaystyle \lim_{n \rightarrow \infty}a_n=\lim_{n \rightarrow \infty}\frac{1}{x^p}=\infty\neq 0.$
Thus, by the Divergence Test, the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ diverges if $p \lt 0.$
In Summary
If $p \gt 1,$ then $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ converges.
If $p \leq 1,$ then $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}$ diverges.
More Examples: Decide if the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{5/4}}$
The $p$-series converges since $p=\frac{5}{4} \gt 1.$
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{4/5}}$
The $p$-series diverges since $p=\frac{4}{5} \lt 1.$
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{1.000000000001}}$
The $p$-series converges since $p=1.000000000001 \gt 1.$
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^{0.999999999999}}$
The $p$-series diverges since $p=0.999999999999 \lt 1.$
$p$-Series: $p=$ $$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^p}$$
| Partial Sum $S_N$ | |||
| $N$ |
Dire Warning #2
$\displaystyle \sum_{n=1}^{\infty}a_n$ GENERALLY DOES NOT EQUAL
$\displaystyle \int_{N}^{\infty}f(x) \, dx$!!!!!!!!!!!!!!!!!!


Case in Point
$$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2}\approx 1.64, \mbox{ but } \displaystyle \int_{1}^{\infty}\frac{1}{x^2} \, dx=1$$
A little bit later, we'll learn the exact value for $\displaystyle \sum_{n=1}^{\infty} \frac{1}{n^2}.$
Hard Fact of Life
Generally speaking, finding exact sums of infinite series is difficult at best.
However, there is a small ray of sunshine...
The Remainder Estimate from the Integral Test
Suppose a convergent series $\displaystyle \sum_{n=1}^{\infty}a_n$ with sum $S$, and a continuous, decreasing function $f$ satisfy all of the conditions of the Integral Test.
Then, letting $S_N$ be the $N$th partial sum $\displaystyle \sum_{n=1}^{N}a_n,$ the remainder $R_N=S-S_N$ satisfies $$\int_{N+1}^{\infty}f(x) \, dx \leq R_N \leq \int_{N}^{\infty}f(x) \, dx$$
Th Big Idea
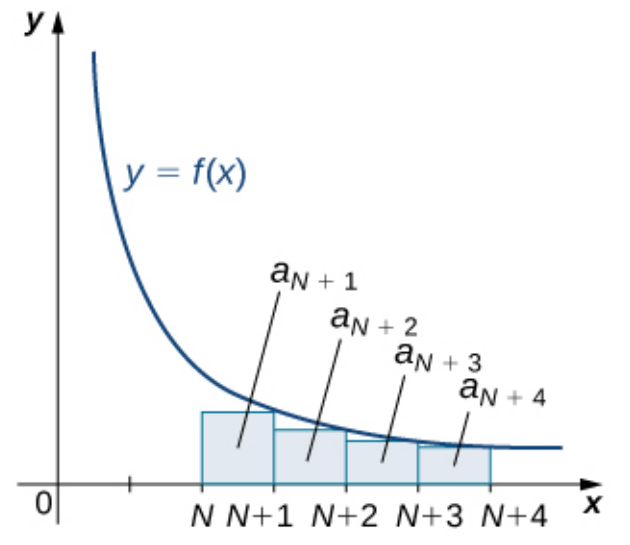 | 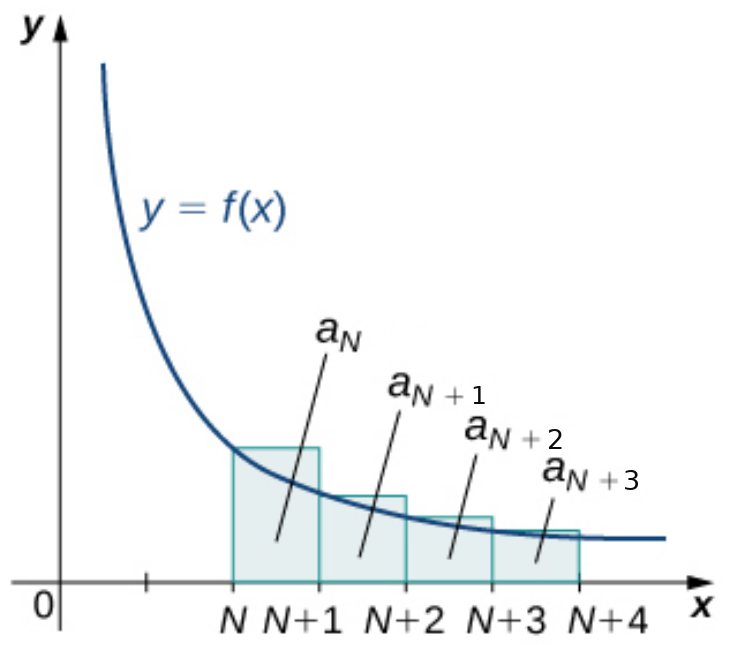 |
| $\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+\cdots \leq \int_{N}^{\infty} f(x) \, dx\,\,\,\,\,$ | $\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+\cdots \geq \int_{N+1}^{\infty} f(x) \, dx$ |
| $R_N$ is a right-hand approximation of integral | $R_N$ is a left-hand approximation of integral |
In Other Words...
$$S_N+\int_{N+1}^{\infty} f(x) \, dx \leq \sum_{n=1}^{\infty}a_n \leq S_N +\int_{N}^{\infty}f(x) \, dx$$
The Remainder Estimate Theorem for the Integral Test allows us to know how close out approximation is.
This, folks, is a ray of sunshine!
Example
1) Estimate $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ with the partial sum $S_{10}.$
2) How many terms $N$ in the partial sum $S_N$ would we need in order to approximate $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ within an error less than $10^{-5}?$
1) We first estimate the sum of the series.
$$
\begin{array}{llll}
&\displaystyle S_N+\int_{N+1}^{\infty} f(x) \, dx \leq \sum_{n=1}^{\infty}a_n \leq S_N +\int_{N}^{\infty}f(x) \, dx&\displaystyle &\mbox{}\\
\implies &\displaystyle S_{10}+\int_{11}^{\infty} \frac{1}{x^2} \, dx \leq \sum_{n=1}^{\infty}\frac{1}{n^2} \leq S_{10} +\int_{10}^{\infty}\frac{1}{x^2} \, dx &\displaystyle &\mbox{}\\
\implies &\displaystyle 1.549767731...+\frac{1}{11} \leq \sum_{n=1}^{\infty}\frac{1}{n^2} \leq 1.549767731... +\frac{1}{10} &\displaystyle &\mbox{}\\
\implies &\displaystyle 1.640676822... \leq \sum_{n=1}^{\infty}\frac{1}{n^2} \leq 1.649767731... &\displaystyle &\mbox{}\\
\end{array}
$$
2) To answer the second part of the question, we must find an $N$ such that $$\displaystyle R_N \leq \int_{N}^{\infty}\frac{1}{x^2} \, dx \leq 10^{-5}.$$
Since $$\displaystyle \int_{N}^{\infty}\frac{1}{x^2} \, dx =\lim_{b\rightarrow \infty}\left[-\frac{1}{x}\right]_{N}^{b}=\lim_{b\rightarrow \infty}\left[-\frac{1}{b}+\frac{1}{N}\right]=\frac{1}{N},$$
the above gives
$$
\begin{array}{llll}
&\displaystyle \frac{1}{N}&\leq 10^{-5}\displaystyle &\mbox{}\\
\implies &\displaystyle N &\geq 10^5\displaystyle &\mbox{}\\
\implies &\displaystyle N &\geq \mbox{10,000}\displaystyle &\mbox{}\\
\end{array}
$$
That is, we would need at least $\mbox{10,000}$ terms to approximate the series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ within an error less than $10^{-5}.$
Historical Sidenote: The Basel Problem. Determine the sum $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2}$ exactly.
The problem was posed in 1650 and was not resolved until 1734 by Leonard Euler. Even the entire Bernoulli Family couldn't figure it out!

Based upon our above estimation, are there any guesses?
$$\displaystyle S=\sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{\pi^2}{6}$$
| Partial Sum $S_N$ | |||
| $N$ |