Question: Has anyone here ever heard of Zeno's paradox of motion?
Zeno's Paradox of Motion: Suppose Mr. Holt needs to get from point A to point B.
First, he must get half way there.
Once he's in the middle, he must get half way from the middle to point B.
Once he's in the 3/4 of the way there, he must get half way from that point to point B...
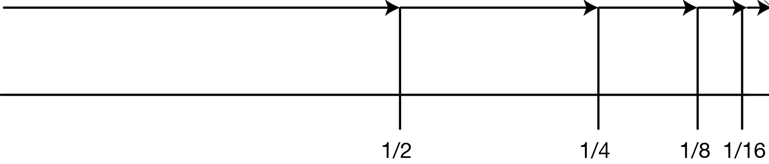
Zeno's Paradox of Motion
Zeno argued that getting from point A to point B (i.e., motion) is impossible since we cannot traverse an infinitude of ever-diminishing distances.
Indeed! How can we add up an infinite number of distances?
Is this even possible?
Example
Consider the sequence $\{\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\ldots\}$
Suppose we add up the first terms of this sequence.
$\displaystyle S_1=\sum_{n=1}^{1}\left(\frac{1}{2}\right)^n=\frac{1}{2}=0.5.$
Infinite Series
Does the sequence of partial sums $\displaystyle S_N=\sum_{n=1}^{N}\left(\frac{1}{2}\right)^n$ appear to be approaching some value?
Infinite Series
We define the sum of all the terms in the sequence $\{\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\ldots\}$ to be the limit of the partial sums. $$\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n =\lim_{N \rightarrow \infty}\sum_{n=1}^{N}\left(\frac{1}{2}\right)^n=\lim_{N \rightarrow \infty} S_N=1.$$
Zeno's Paradox Redux
Can we add up an infinite number of distances?
Yes! We just did!
Bonus Question: How far did Mr. Holt walk to get from point A to point B?
Graph of the $n$th Partial Sum: $\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n$
| Partial Sum $S_N$ | |||
| $N$ |
Infinite Series
Let $\{a_n\}$ be sequence of real numbers.
An infinite series is an expression of the form $$\displaystyle \sum_{n=1}^{\infty}a_n=a_1+a_2+\cdots+a_k+\cdots$$ We define sequence of partial sums $\{S_N\}$ to be given by $$\displaystyle S_N=\sum_{n=1}^{N}a_n=a_1+a_2+\cdots+a_N$$ If $\displaystyle \lim_{N \rightarrow \infty} S_N=S$ and $S$ is a real number, then we say that the series converges to $S.$ Otherwise, the series diverges.
Example
The series $\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n$ converges to $1$ since the sequence of partial sums $\displaystyle S_N=\sum_{n=1}^{N}\left(\frac{1}{2}\right)^n$ converges to $1.$
Example: Use the sequence of partial sums to determine whether the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n(n+1)}$
Looking at terms of the sequence of partial sums:
$\displaystyle S_1=\sum_{n=1}^{1}\frac{1}{n(n+1)}=\frac{1}{2}.$
$\displaystyle \{S_N\}=\{\frac{1}{2},\ldots\}$
Example: Use the sequence of partial sums to determine whether the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}\frac{n+3}{n}$
Looking at terms of the sequence of partial sums:
$\displaystyle S_1=\sum_{n=1}^{1}\frac{n+3}{n}=4.$
$\displaystyle \{S_N\}=\{4,\ldots\}$
Example: Use the sequence of partial sums to determine whether the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}(1+(-1)^{n+1})$
Looking at terms of the sequence of partial sums:
$\displaystyle S_1=\sum_{n=1}^{1}(1+(-1)^{n+1})=2.$
$\displaystyle \{S_N\}=\{2,\ldots\}$
Example: Use the sequence of partial sums to determine whether the series converges or diverges.
$\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)$ Looking at terms of the sequence of partial sums:
$\displaystyle S_1=\sum_{n=1}^{1}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)=1-\frac{1}{\sqrt{2}}.$
$\displaystyle \{S_N\}=\{1-\frac{1}{\sqrt{2}},\ldots\}$
Properties of Convergent Series
Let $\displaystyle \sum_{n=1}^{\infty}a_n$ and $\displaystyle \sum_{n=1}^{\infty}b_n$ be convergent series. Then
$\displaystyle \sum_{n=1}^{\infty}(a_n+b_n)=\sum_{n=1}^{\infty}a_n+\sum_{n=1}^{\infty}b_n$
$\displaystyle \sum_{n=1}^{\infty}(a_n-b_n)=\sum_{n=1}^{\infty}a_n-\sum_{n=1}^{\infty}b_n$
$\displaystyle \sum_{n=1}^{\infty}c a_n=c\sum_{n=1}^{\infty}a_n$
Example: Using Properties of Convergent Series
$\displaystyle \sum_{n=1}^{\infty}7\left(\frac{1}{5}\left(\frac{1}{2}\right)^n+\frac{3}{n(n+1)}\right)$
$$
\begin{array}{lll}
\displaystyle \sum_{n=1}^{\infty}7\left(\frac{1}{5}\left(\frac{1}{2}\right)^n+\frac{3}{n(n+1)}\right) &=\displaystyle 7\sum_{n=1}^{\infty}\left(\frac{1}{5}\left(\frac{1}{2}\right)^n+\frac{3}{n(n+1)}\right) &\mbox{}\\
&=\displaystyle 7\left[\sum_{n=1}^{\infty}\left(\frac{1}{5}\left(\frac{1}{2}\right)^n\right)+\sum_{n=1}^{\infty}\frac{3}{n(n+1)}\right] &\mbox{}\\
&=\displaystyle 7\left[\frac{1}{5}\sum_{n=1}^{\infty}\left(\frac{1}{2}\right)^n+3\sum_{n=1}^{\infty}\frac{1}{n(n+1)}\right] &\mbox{}\\
&=\displaystyle 7\left[\frac{1}{5}\cdot 1+3\cdot 1\right] &\mbox{}\\
&=\displaystyle \frac{112}{5} &\mbox{}\\
&=\displaystyle 22.4 &\mbox{}\\
\end{array}
$$
Important Example: The Harmonic Series $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$
Does the harmonic series converge or diverge?
The Harmonic Series $$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n}$$
| Partial Sum $S_N$ | |||
| $N$ |
Does the Harmonic Series Converge?
$$ \begin{array}{|l|l|} \hline N & S_N\\ \hline \mbox{10} &2.92897\\ \mbox{100} &5.18738\\ \mbox{1000} & 7.48547\\ \mbox{10,000} &9.78761\\ \mbox{100,000} &12.09015\\ \mbox{1,000,000} &14.39273\\ \hline \end{array} $$ What do you think?
Answer
The harmonic series diverges, but very slowly.
In fact, the sum of the first $10^{43}$ terms is still less than $100.$ (Wow!)
Despite being a divergent series, the harmonic series is still actually quite useful and interesting!
We'll have more to say about the harmonic series in future sections.
In the next section we'll show that the the harmonic series does indeed diverge to $\infty.$
For now, though...
Geometric Series
A Geometric Series is an infinite series of the form $\displaystyle \sum_{n=1}^{\infty} ar^{n-1}.$
Geometric series have applications in probability and modelling certain kinds discrete processes.
To decide when this series converges or diverges (this will depend on the value of $r$), we must first derive an expression for the partial sums.
We shall find a closed-form expression for the $N$th partial sum
$$\displaystyle S_N=\sum_{n=1}^{N} ar^{n-1}=a\left(1+r+r^2+\cdots+r^{N-1}\right)$$
Multiplying both side of the above by $r-1$ gives
$$
\begin{array}{lll}
\displaystyle (1-r)S_N&=a(1-r)\left(1+r+r^2+\cdots+r^{N-1}\right) &\mbox{}\\
&=a\left[\left(1+r+r^2+\cdots+r^{N-1}\right)-\left(r+r^2+r^3+\cdots+r^{N}\right)\right] &\mbox{}\\
&=a\left(1-r^{N}\right) &\mbox{}\\
\end{array}
$$
Thus,
$$
\displaystyle S_N=\sum_{n=1}^{N} ar^{n-1}=a\left(1+r+r^2+\cdots+r^{N-1}\right)=\frac{a(1-r^N)}{1-r}
$$
Geometric Series
A Geometric Series $\displaystyle \sum_{n=1}^{\infty} ar^{n-1}$ converges if $|r|\lt 1$ and diverges if $|r|\geq 1.$
If $|r| \lt 1,$ then $\displaystyle \sum_{n=1}^{\infty} ar^{n-1}=\frac{a}{1-r}$
Examples: Geometric Series
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{9}\left(\frac{1}{3}\right)^{n-1}$
$$
\begin{array}{lll}
\displaystyle \sum_{n=1}^{\infty} \frac{1}{9}\left(\frac{1}{3}\right)^{n-1}&=\displaystyle \frac{\frac{1}{9}}{1-\frac{1}{3}}&\mbox{}\\
&=\displaystyle \frac{1}{9-3}&\mbox{}\\
&=\displaystyle \frac{1}{6}&\mbox{}\\
\end{array}
$$
$\displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n-1}5}{4^{n-1}}$
$$
\begin{array}{lll}
\displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n-1}5}{4^{n-1}}&=\displaystyle \sum_{n=1}^{\infty} 5\left(-\frac{1}{4}\right)^{n-1}&\mbox{}\\
&=\displaystyle \frac{5}{1-\left(-\frac{1}{4}\right)}&\mbox{}\\
%&=\displaystyle \frac{5}{1+\frac{1}{4}}&\mbox{}\\
%&=\displaystyle \frac{20}{4+1}&\mbox{}\\
%&=\displaystyle \frac{20}{5}&\mbox{}\\
&=\displaystyle 4&\mbox{}\\
\end{array}
$$
Find the value of the decimal $0.\overline{7}=0.7777\ldots$
$$
\begin{array}{lll}
\displaystyle 0.7777\ldots&=\displaystyle 7\cdot \left(\frac{1}{10}\right)^{1}+7\cdot \left(\frac{1}{10}\right)^{2}+7\cdot \left(\frac{1}{10}\right)^{3}+\cdots &\mbox{}\\
&=\displaystyle \sum_{n=1}^{\infty} 7\left(\frac{1}{10}\right)^{n} &\mbox{}\\
&=\displaystyle \sum_{n=1}^{\infty} \frac{7}{10}\left(\frac{1}{10}\right)^{n-1} &\mbox{}\\
&=\displaystyle \frac{\frac{7}{10}}{1-\frac{1}{10}} &\mbox{}\\
&=\displaystyle \frac{7}{9}&\mbox{}\\
\end{array}
$$
Example: Geometric Series
A bouncy ball is released from rest at a height of $2$ meters seen in the photo below. The height of each successive bounce is $\frac{1}{2}$ the height of the previous bounce. Find the vertical distance the ball will have travelled after it finishes bouncing.
Geometric Series: $a=$ and $r=$ $$\displaystyle\sum_{n=1}^{\infty}a r^{n-1}$$
| Partial Sum $S_N$ | |||
| $N$ |
Telescoping Series
Let's begin with an example: $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n(n+1)}$
We saw from a previous example that the $N$th partial sum is
$$S_N=\sum_{n=1}^{N}\frac{1}{n(n+1)}=\frac{N}{N+1}$$ so that
$$\sum_{n=1}^{\infty}\frac{1}{n(n+1)}=\lim_{N \rightarrow \infty} S_N=\lim_{N \rightarrow \infty} \frac{N}{N+1}=1$$
However, our method for obtaining the expression for the partial sum was rather clumsy.
Here we will systematically obtain an expression by rewriting the expression $\displaystyle \frac{1}{n(n+1)}$ in a new way: $$ \frac{1}{n(n+1)}=\frac{A}{n}+\frac{B}{n+1} $$ That's right, partial fractions are back! :D Like before, we set to the task of building up denominators. $$ \frac{A}{n}+\frac{B}{n+1}=\frac{A(n+1)}{n(n+1)}+\frac{Bn}{n(n+1)}=\frac{(A+B)n+A}{n(n+1)} $$ We see that $(A+B)n+A$ must equal $1$ so that $A=1$ and and $A+B=0.$ Then $A=1$ and $B=-1.$ That is, $$ \frac{1}{n(n+1)}=\frac{1}{n}+\frac{-1}{n+1}=\frac{1}{n}-\frac{1}{n+1} $$ We can now see this series for what it truly is. Let's now look at the rewritten series. $$ \displaystyle \sum_{n=1}^{\infty}\frac{1}{n(n+1)}=\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}\right) $$ Finding the $N$th partial sum is now a much easier task: $$ \begin{array}{ll} S_N&=\displaystyle \sum_{n=1}^{N}\frac{1}{n(n+1)}\\ &=\displaystyle \sum_{n=1}^{N}\left(\frac{1}{n}-\frac{1}{n+1}\right)\\ &=\displaystyle \left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\cdots+\left(\frac{1}{N-1}-\frac{1}{N}\right)+\left(\frac{1}{N}-\frac{1}{N+1}\right)\\ &=\displaystyle 1-\frac{1}{N+1}\\ &=\displaystyle \frac{N}{N+1}\\ \end{array} $$ From here, we may find the sum of the series as we did above.
The above series is called a telescoping series since all the inner terms collapse in on themselves... like a telescope!
Here we will systematically obtain an expression by rewriting the expression $\displaystyle \frac{1}{n(n+1)}$ in a new way: $$ \frac{1}{n(n+1)}=\frac{A}{n}+\frac{B}{n+1} $$ That's right, partial fractions are back! :D Like before, we set to the task of building up denominators. $$ \frac{A}{n}+\frac{B}{n+1}=\frac{A(n+1)}{n(n+1)}+\frac{Bn}{n(n+1)}=\frac{(A+B)n+A}{n(n+1)} $$ We see that $(A+B)n+A$ must equal $1$ so that $A=1$ and and $A+B=0.$ Then $A=1$ and $B=-1.$ That is, $$ \frac{1}{n(n+1)}=\frac{1}{n}+\frac{-1}{n+1}=\frac{1}{n}-\frac{1}{n+1} $$ We can now see this series for what it truly is. Let's now look at the rewritten series. $$ \displaystyle \sum_{n=1}^{\infty}\frac{1}{n(n+1)}=\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{n}-\frac{1}{n+1}\right) $$ Finding the $N$th partial sum is now a much easier task: $$ \begin{array}{ll} S_N&=\displaystyle \sum_{n=1}^{N}\frac{1}{n(n+1)}\\ &=\displaystyle \sum_{n=1}^{N}\left(\frac{1}{n}-\frac{1}{n+1}\right)\\ &=\displaystyle \left(1-\frac{1}{2}\right)+\left(\frac{1}{2}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{4}\right)+\cdots+\left(\frac{1}{N-1}-\frac{1}{N}\right)+\left(\frac{1}{N}-\frac{1}{N+1}\right)\\ &=\displaystyle 1-\frac{1}{N+1}\\ &=\displaystyle \frac{N}{N+1}\\ \end{array} $$ From here, we may find the sum of the series as we did above.
The above series is called a telescoping series since all the inner terms collapse in on themselves... like a telescope!
Telescoping Series
"Telescoping" occurs when most of the terms in the partial sums of a series cancel out and collapse down...
Another Telescoping Example We've Seen
$$ \begin{array}{ll} \displaystyle S_{N}&=\displaystyle \sum_{n=1}^{N}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\\ &\displaystyle =\left(\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}\right)+\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}\right)+\left(\frac{1}{\sqrt{3}}-\frac{1}{\sqrt{4}}\right)+\cdots+\left(\frac{1}{\sqrt{N-1}}-\frac{1}{\sqrt{N}}\right)+\left(\frac{1}{\sqrt{N}}-\frac{1}{\sqrt{N+1}}\right)\\ &\displaystyle =1-\frac{1}{\sqrt{N+1}}\\ \end{array} $$ Thus, $$ \sum_{n=1}^{\infty}\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)=\lim_{N\rightarrow\infty}S_N=1 $$
Telescoping Series
Examples: Telescoping Series
$\displaystyle \sum_{n=1}^{\infty}\left(\frac{3}{n^2}-\frac{3}{(n+1)^2}\right)$
Let's use the telescoping property already built into this series to find an expression for the $N$th partial sum.
$$
\begin{array}{l}
S_N=\displaystyle \sum_{n=1}^{N}\left(\frac{3}{n^2}-\frac{3}{(n+1)^2}\right)\\
=\displaystyle 3\sum_{n=1}^{N}\left(\frac{1}{n^2}-\frac{1}{(n+1)^2}\right)\\
=\displaystyle 3\left[\left(1-\frac{1}{4}\right)+\left(\frac{1}{4}-\frac{1}{9}\right)+\left(\frac{1}{9}-\frac{1}{25}\right)+\cdots+\left(\frac{1}{(N-1)^2}-\frac{1}{N^2}\right)+\left(\frac{1}{N^2}-\frac{1}{(N+1)^2}\right)\right]\\
=\displaystyle 3\left[1-\frac{1}{(N+1)^2}\right]\\
\end{array}
$$
Thus
$$
\sum_{n=1}^{\infty}\left(\frac{3}{n^2}-\frac{3}{(n+1)^2}\right)=\lim_{N\rightarrow\infty}S_N=3
$$
$\displaystyle \sum_{n=1}^{\infty} \frac{4}{(4n-3)(4n+1)}$
We first use partial fractions to rewrite the expression.
$$
\frac{4}{(4n-3)(4n+1)}=\frac{A}{4n-3}+\frac{B}{4n+1}
$$
Building up denominators,
$$
\begin{array}{ll}
\displaystyle \frac{A}{4n-3}+\frac{B}{4n+1}&=\displaystyle \frac{A(4n+1)}{(4n-3)(4n+1)}+\frac{B(4n-3)}{(4n-3)(4n+1)}\\
&=\displaystyle \frac{(4A+4B)n+(A-3B)}{(4n-3)(4n+1)}\\
\end{array}
$$
Equating coefficients, we have the system
$$
\begin{cases}
4A+4B=0\\
A-3B=4
\end{cases}
$$
Solving this system...
...we have $A=1$ and $B=-1.$
Then $$ \frac{4}{(4n-3)(4n+1)}=\frac{A}{4n-3}+\frac{B}{4n+1}=\frac{1}{4n-3}-\frac{1}{4n+1} $$ Rewriting the series, $$ \displaystyle \sum_{n=1}^{\infty} \frac{4}{(4n-3)(4n+1)}=\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{4n-3}-\frac{1}{4n+1}\right) $$ Finding the $N$th partial sum $$ \begin{array}{ll} S_N&=\displaystyle \sum_{n=1}^{N} \frac{4}{(4n-3)(4n+1)}\\ &=\displaystyle \sum_{n=1}^{N}\left(\frac{1}{4n-3}-\frac{1}{4n+1}\right)\\ &=\displaystyle \left(1-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{9}\right)+\left(\frac{1}{9}-\frac{1}{13}\right)+\cdots+\left(\frac{1}{4N-7}-\frac{1}{4N-3}\right)+\left(\frac{1}{4N-3}-\frac{1}{4N+1}\right)\\ &=\displaystyle 1-\frac{1}{4N+1}\\ \end{array} $$ Thus, $$ \sum_{n=1}^{\infty} \frac{4}{(4n-3)(4n+1)}=\lim_{N\rightarrow \infty} S_N=1 $$
...we have $A=1$ and $B=-1.$
Then $$ \frac{4}{(4n-3)(4n+1)}=\frac{A}{4n-3}+\frac{B}{4n+1}=\frac{1}{4n-3}-\frac{1}{4n+1} $$ Rewriting the series, $$ \displaystyle \sum_{n=1}^{\infty} \frac{4}{(4n-3)(4n+1)}=\displaystyle \sum_{n=1}^{\infty}\left(\frac{1}{4n-3}-\frac{1}{4n+1}\right) $$ Finding the $N$th partial sum $$ \begin{array}{ll} S_N&=\displaystyle \sum_{n=1}^{N} \frac{4}{(4n-3)(4n+1)}\\ &=\displaystyle \sum_{n=1}^{N}\left(\frac{1}{4n-3}-\frac{1}{4n+1}\right)\\ &=\displaystyle \left(1-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{9}\right)+\left(\frac{1}{9}-\frac{1}{13}\right)+\cdots+\left(\frac{1}{4N-7}-\frac{1}{4N-3}\right)+\left(\frac{1}{4N-3}-\frac{1}{4N+1}\right)\\ &=\displaystyle 1-\frac{1}{4N+1}\\ \end{array} $$ Thus, $$ \sum_{n=1}^{\infty} \frac{4}{(4n-3)(4n+1)}=\lim_{N\rightarrow \infty} S_N=1 $$
$\displaystyle \sum_{n=1}^{\infty} \ln \left(\sqrt{1+\frac{1}{n}}\right)$
We rewrite the series to reveal its telescoping nature,
$$
\begin{array}{lll}
\displaystyle \sum_{n=1}^{\infty} \ln \left(\sqrt{1+\frac{1}{n}}\right)&=\displaystyle \sum_{n=1}^{\infty} \ln \left(\sqrt{1+\frac{1}{n}}\right)&\mbox{}\\
&=\displaystyle \sum_{n=1}^{\infty} \ln \left(1+\frac{1}{n}\right)^{1/2}&\mbox{}\\
&=\displaystyle \sum_{n=1}^{\infty} \frac{1}{2}\ln \left(\frac{n+1}{n}\right)&\mbox{}\\
&=\displaystyle \frac{1}{2}\sum_{n=1}^{\infty} \left(\ln(n+1)-\ln(n)\right)&\mbox{}\\
\end{array}
$$
Examining the partial sums,
$$
\begin{array}{ll}
S_1=\left(\ln(2)-0\right)=\ln 2\\
S_2=\left(\ln(2)-0\right)+ \left(\ln(3)-\ln(2)\right)=\ln 3\\
S_3=\left(\ln(2)-0\right)+ \left(\ln(3)-\ln(2)\right)+ \left(\ln(4)-\ln(3)\right)=\ln 4\\
\vdots\\
S_N=\left(\ln(2)-0\right)+ \left(\ln(3)-\ln(2)\right)+\cdots+ \left(\ln(N)-\ln(N-1)\right)+ \left(\ln(N+1)-\ln(N)\right)=\ln(N+1)
\end{array}
$$
Since $\displaystyle \lim_{N\rightarrow \infty} S_N=\infty,$ the series diverges to $\infty.$
Bonus Example: Find the area of the Sierpinski Triangle as drawn below in the second figure.
Iteration $0:$ Begin with a whole triangle of area $\displaystyle \frac{1}{2}.$
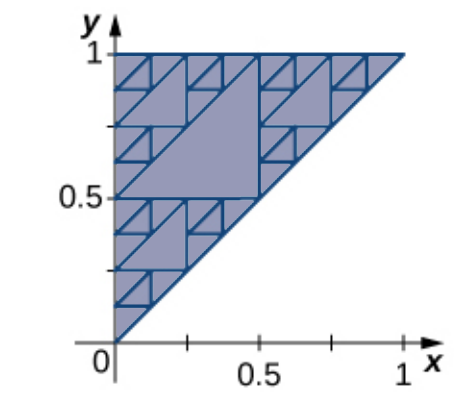
Iteration $1:$ Subtract $1$ middle triangle of area $\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2}\right)^2$
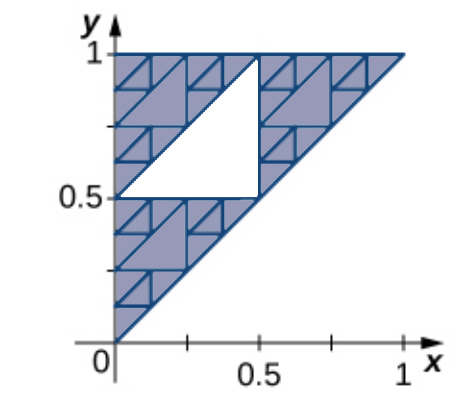Iteration $2:$ From the $3$ remaining triangles, subtract $3$ middle triangles of area $\displaystyle \frac{1}{2}\cdot \left(\frac{1}{4}\right)^2$
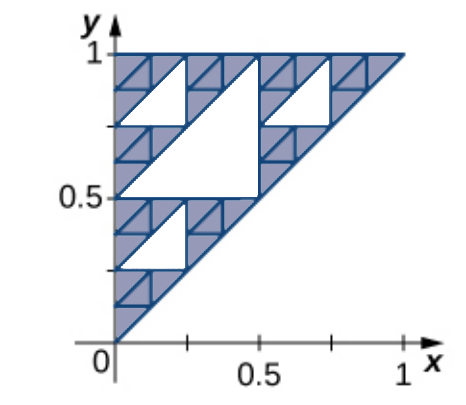The total subtracted area is now $$\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2}\right)^2+3\cdot \frac{1}{2}\cdot \left(\frac{1}{4}\right)^2$$
Iteration $3:$ From the $9$ remaining triangles, subtract $9$ middle triangles of area $\displaystyle \frac{1}{2}\cdot \left(\frac{1}{8}\right)^2$
The total subtracted area is now $$\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2}\right)^2+3\cdot \frac{1}{2}\cdot \left(\frac{1}{4}\right)^2+9\cdot \frac{1}{2}\cdot \left(\frac{1}{8}\right)^2$$
$$\vdots$$
Iteration $N:$ From the $3^{N-1}$ remaining triangles, subtract $3^{N-1}$ middle triangles of area $\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2^{N}}\right)^2$
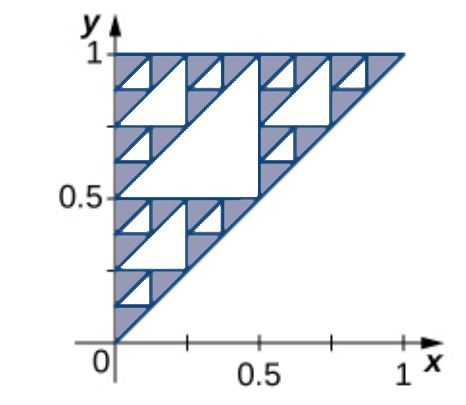The total subtracted area is now
$$\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2}\right)^2+3\cdot \frac{1}{2}\cdot \left(\frac{1}{4}\right)^2+9\cdot \frac{1}{2}\cdot \left(\frac{1}{8}\right)^2+\cdots+3^{N-1}\cdot\frac{1}{2}\cdot \left(\frac{1}{2^{N}}\right)^2$$
In the limit, the area subtracted from the original triangle is $$ \begin{array}{ll} \displaystyle \sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{2}\cdot\left(\frac{1}{2^n}\right)^2&=\displaystyle \sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{2}\cdot \frac{1}{2^{2n}}\\ &\displaystyle =\sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{8}\cdot \frac{1}{2^{2n-2}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{2^{2(n-1)}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{(2^2)^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{4^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}\frac{3^{n-1}}{4^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}\left(\frac{3}{4}\right)^{n-1}\\ &\displaystyle =\frac{1}{8}\frac{1}{1-\frac{3}{4}}\\ &\displaystyle =\frac{1}{8}\cdot 4\\ &\displaystyle =\frac{1}{2}\\ \end{array} $$ That is to say that, in the limit, we subtract off ALL of the area!
Conclusion:
Duhn! Duhn! Duuuuhhhun!
Iteration $1:$ Subtract $1$ middle triangle of area $\displaystyle \frac{1}{2}\cdot \left(\frac{1}{2}\right)^2$
In the limit, the area subtracted from the original triangle is $$ \begin{array}{ll} \displaystyle \sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{2}\cdot\left(\frac{1}{2^n}\right)^2&=\displaystyle \sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{2}\cdot \frac{1}{2^{2n}}\\ &\displaystyle =\sum_{n=1}^{\infty}3^{n-1}\cdot\frac{1}{8}\cdot \frac{1}{2^{2n-2}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{2^{2(n-1)}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{(2^2)^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}3^{n-1}\cdot \frac{1}{4^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}\frac{3^{n-1}}{4^{n-1}}\\ &\displaystyle =\frac{1}{8}\sum_{n=1}^{\infty}\left(\frac{3}{4}\right)^{n-1}\\ &\displaystyle =\frac{1}{8}\frac{1}{1-\frac{3}{4}}\\ &\displaystyle =\frac{1}{8}\cdot 4\\ &\displaystyle =\frac{1}{2}\\ \end{array} $$ That is to say that, in the limit, we subtract off ALL of the area!
Conclusion:
The Sierpinski Triangle has an area of $0!$
Duhn! Duhn! Duuuuhhhun!