We begin the course with a fundamental notion.
Sequences
Sequences are of fundamental importance to mathematics in general, but they are also one of the workhorses of applied mathematics. You will find sequences popping up in...
- discrete-time models (growth and decay models)
- numerical implementations of continuous-time phenomena
- solutions to differential equations which model phenomena as diverse as
- wave propagation
- heat transfer
- diffusion of information in populations
- flu epidemics
- electric flow in circuits
- acoustics/signal processing
- stochastic processes (Markov Chains, Poisson Processes, etc)
- pseudo-random number generation (for data encryption and simulating stochastic processes)
Sequences
Very roughly speaking, sequences are ordered collections of real numbers.
In this class, we will mostly be concerned with infinite sequences.
Examples
$\displaystyle \{a_n\}=\{\sqrt{1},\sqrt{2},\sqrt{3},\ldots,\sqrt{n},\ldots\}$
$\displaystyle \{b_n\}=\{1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\ldots,(-1)^{n+1}\frac{1}{n},\ldots\}$
$\displaystyle \{c_n\}=\{0,\frac{1}{2},\frac{2}{3},\frac{3}{4},\ldots,\frac{n-1}{n},\ldots\}$
$\displaystyle \{d_n\}=\{1,-1,1,-1,\ldots,(-1)^{n+1},\ldots\}$
The numbers in the sequence are called terms, and most often we will specify a sequence by simply listing a formula for its terms. We may specify the above sequences as simply
$a_n=\sqrt{n},$ $\displaystyle \,\,\,\,b_n=(-1)^{n+1}\frac{1}{n},$ $\displaystyle \,\,\,\,c_n=\frac{n-1}{n},\,\,\,\,$ and $\,\,\,\,d_n=(-1)^{n+1}.$
The number which specifies the place of a number in a sequence (as $n$ above does) is called the index.
Graphing Sequences $$a_n=\sqrt{n}$$
| $a_n$ | |||
| $n$ |
$$b_n=(-1)^{n+1}\frac{1}{n}$$
| $b_n$ | |||
| $n$ |
$$c_n=\frac{n-1}{n}$$
| $c_n$ | |||
| $n$ |
$$d_n=(-1)^{n+1}$$
| $d_n$ | |||
| $n$ |
Recurrence Relations
The definitions of the above sequences give an explicit formula for the value of a term in terms of its index.
We shall now look at another very common way of defining sequences: recurrence relations.
Recurrence Relations
A recurrence relation states the value of a sequence in terms of its previous value. In this way, an initial value must also be specified.
Example: Define a sequence with $a_1=2$ and to get the next value in the sequence we add $3.$ That is, $\displaystyle a_{n+1}=a_n+3.$
The above is called an arithmetic sequence since the difference of successive terms is constant.
Example: Define a sequence with $a_1=4$ and to get the next value in the sequence we multiply by $\frac{1}{2}.$ That is, $\displaystyle a_{n+1}=\frac{1}{2}a_n.$
The above is called a geometric sequence since the ratio of successive terms is constant.
Recurrence Relations
Example: Define a sequence with $F_1=1$ and $F_2=1$. To get the next value in the sequence we add the previous $2$ terms. That is, $\displaystyle F_{n+1}=F_n+F_{n-1}.$
The above sequence is called the Fibonacci Sequence. This sequence appears in lots of interesting places in nature and in pure mathematics.

Recurrence Relations
Example: Define a sequence with $x_1=2$ and $\displaystyle x_{n+1}=x_n-\frac{x_n^2-2}{2x_n}.$
| $x_n$ | |||
| $n$ |
Finding Formulas
In the coming sections, there will be times when we need to find formulas for the $n$th term of a sequence. For each of the following sequences, find an explicit formula for the $n$th term of the sequence.
$\displaystyle \{a_n\}=\{1,5,9,13,17,\ldots\}$ $\displaystyle \,\,\,\,\,\,a_n=4n-3$
$\displaystyle \{a_n\}=\{\frac{1}{2},\frac{2}{3},\frac{3}{4},\frac{4}{5},\frac{5}{6},\ldots\}$ $\displaystyle \,\,\,\,\,\,a_n=\frac{n}{n+1}$
$\displaystyle \{a_n\}=\{\frac{5}{1},\frac{8}{2},\frac{11}{6},\frac{14}{24},\frac{17}{120},\ldots\}$ $\displaystyle \,\,\,\,\,\,a_n=\frac{3n+2}{n!}$
$\displaystyle \{a_n\}=\{\frac{1}{25},\frac{8}{125},\frac{27}{625},\frac{64}{3125},\frac{125}{15625},\ldots\}$ $\displaystyle \,\,\,\,\,\,a_n=\frac{n^3}{5^{n+1}}$
$\displaystyle \{a_n\}=\{0,1,0,1,0,1,\ldots\}$ $\displaystyle \,\,\,\,\,\,a_n=\frac{1+(-1)^n}{2}$
The Long-Term Behavior of Sequences
A theme we will be particularly interested in in this course is the long-term behavior of sequences.
To better understand what we mean by this, let's recall our initial examples:
$\displaystyle \{a_n\}=\{\sqrt{1},\sqrt{2},\sqrt{3},\ldots,\sqrt{n},\ldots\}$
$\displaystyle \{b_n\}=\{1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\ldots,(-1)^{n+1}\frac{1}{n},\ldots\}$
$\displaystyle \{c_n\}=\{0,\frac{1}{2},\frac{2}{3},\frac{3}{4},\ldots,\frac{n-1}{n},\ldots\}$
$\displaystyle \{d_n\}=\{1,-1,1,-1,\ldots,(-1)^{n+1},\ldots\}$
What do the above sequences do in the long run?
Convergent Sequences
A very important type of long-term behavior of a sequence is convergence.
The above sequences which seem to "settle in" on a value as $n$ gets large converge to a value. What value does the sequence $$\{c_n\}=\{0,\frac{1}{2},\frac{2}{3},\frac{3}{4},\ldots,\frac{n-1}{n},\ldots\}$$ seem to "settle in" on?
Convergent Sequences
Loosely speaking, a sequence converges to a value $L$ if we can make the sequence as close to $L$ as we like by making $n$ large enough.
In this case we write $\displaystyle \lim_{n \rightarrow \infty} a_n=L.$
The next definition makes the above notion precise.
Convergent Sequences
A sequence $\{a_n\}$ is said to converge to $L$ if for all $\varepsilon \gt 0,$ we can find a positive integer $N$ such that $$n \gt N \,\,\,\,\mbox{ implies }\,\,\,\, |a_n-L|\lt \varepsilon.$$ In this case we write $\displaystyle \lim_{n \rightarrow \infty} a_n=L$ and we say that the limit of the sequence is $L.$
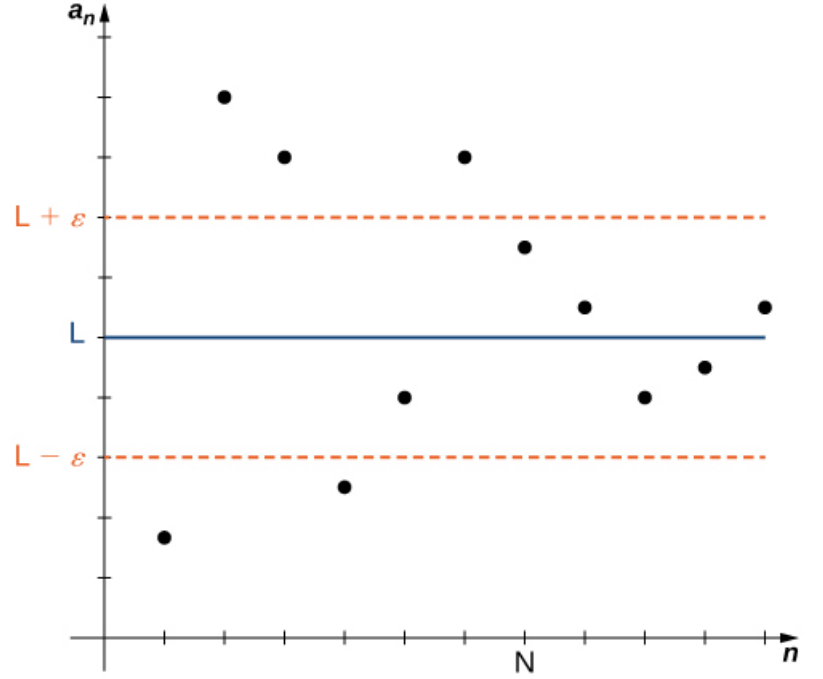
Convergent Sequences
$\displaystyle \lim_{x \rightarrow \infty} a_n=L$ means:
for any $\varepsilon \gt 0$ we choose,
we can find a positive integer $N$ such that
$n \gt N$ (any $n$-value in pink region)
guarantees that $|a_n-L| \lt \varepsilon$
(beyond $N$, $a_n$-values are ALL in blue strip)
for any $\varepsilon \gt 0$ we choose,
we can find a positive integer $N$ such that
$n \gt N$ (any $n$-value in pink region)
guarantees that $|a_n-L| \lt \varepsilon$
(beyond $N$, $a_n$-values are ALL in blue strip)
Divergent Sequences
If a sequence $\{a_n\}$ does not converge to any value $L,$ then we say the sequence diverges. In this case we say that the limit does not exist.
Convergent Sequences
Use the definition of convergence to prove the following limits.
$\displaystyle \lim_{n \rightarrow \infty} \frac{1}{n}=0$
Let $\varepsilon \gt 0.$ Choose $\displaystyle N=\frac{1}{\varepsilon}.$
Then,
$$
\begin{array}{llll}
&\displaystyle n \gt N&\displaystyle &\mbox{}\\
\implies &\displaystyle n \gt \frac{1}{\varepsilon}&\displaystyle &\mbox{}\\
\implies &\displaystyle \varepsilon \gt \frac{1}{n}&\displaystyle &\mbox{}\\
\implies &\displaystyle \left|a_n-L\right|=\left|\frac{1}{n}-0\right|\lt\varepsilon&\displaystyle &\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} 2=2$
Let $\varepsilon \gt 0.$ Choose $\displaystyle N=1.$
Then,
$$
\begin{array}{llll}
&\displaystyle n \gt N&\displaystyle &\mbox{}\\
\implies &\displaystyle n \gt 1&\displaystyle &\mbox{}\\
\implies &\displaystyle \left|a_n-L\right|=\left|2-2\right|=0\lt\varepsilon&\displaystyle &\mbox{}\\
\end{array}
$$
Limit Laws
Limits preserve all the usual arithmetic operations! Suppose $\displaystyle \lim_{n \rightarrow \infty} a_n=L$ and $\displaystyle \lim_{n \rightarrow \infty} b_n=M.$
$\displaystyle \lim_{n \rightarrow \infty} (a_n+b_n) =\lim_{n \rightarrow \infty} a_n+ \lim_{n \rightarrow \infty} b_n =L+M$
$\displaystyle \lim_{n \rightarrow \infty} (a_n-b_n) =\lim_{n \rightarrow \infty} a_n - \lim_{n \rightarrow \infty} b_n =L-M$
$\displaystyle \lim_{n \rightarrow \infty} (a_n \cdot b_n) =\lim_{n \rightarrow \infty} a_n \cdot \lim_{n \rightarrow \infty} b_n =L \cdot M$
$\displaystyle \lim_{n \rightarrow \infty} (k a_n) =k \lim_{n \rightarrow \infty} a_n =k L$
$\displaystyle \lim_{n \rightarrow \infty} \frac{a_n}{b_n} =\frac{\displaystyle\lim_{n \rightarrow \infty} a_n}{\displaystyle\lim_{n \rightarrow \infty} b_n} =\frac{L}{M}$ provided $M \neq 0$
$\displaystyle \lim_{n \rightarrow \infty} c=c$
Examples
Use the limit laws to find each limit.
$\displaystyle \lim_{n \rightarrow \infty} \left(-\frac{1}{n}\right)$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left(-\frac{1}{n}\right)&=\displaystyle -\lim_{n \rightarrow \infty}\frac{1}{n}&\mbox{bring out constant multiple of $-1$}\\
&=\displaystyle 0&\mbox{by previous example}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{n-1}{n}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \frac{n-1}{n}&=\displaystyle \lim_{n \rightarrow \infty} \left(1-\frac{1}{n}\right)&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} 1- \lim_{n \rightarrow \infty}\frac{1}{n}&\mbox{limit of a difference is the difference of the limits}\\
&=\displaystyle 1-0&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{5}{n^2}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \frac{5}{n^2}&=\displaystyle \lim_{n \rightarrow \infty} 5 \cdot \frac{1}{n}\cdot \frac{1}{n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} 5 \cdot \lim_{n \rightarrow \infty} \frac{1}{n} \cdot \lim_{n \rightarrow \infty}\frac{1}{n}&\mbox{limit of a product is the product of the limits}\\
&=\displaystyle 5 \cdot 0 \cdot 0&\mbox{}\\
&=\displaystyle 0&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{4-7n^6}{n^6+3}$
We first note that
$$
\begin{array}{lll}
\displaystyle \frac{4-7n^6}{n^6+3}&=\displaystyle \frac{4-7n^6}{n^6+3}\frac{\frac{1}{n^6}}{\frac{1}{n^6}}&\mbox{}\\
&=\displaystyle \frac{\displaystyle\frac{4}{n^6}-7}{\displaystyle1+\frac{3}{n^6}}&\mbox{}\\
\end{array}
$$
Then
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \frac{4-7n^6}{n^6+3}&=\displaystyle \lim_{n \rightarrow \infty} \frac{\displaystyle\frac{4}{n^6}-7}{\displaystyle1+\frac{3}{n^6}}&\mbox{}\\
&=\displaystyle \frac{\displaystyle\lim_{n \rightarrow \infty} \left(\frac{4}{n^6}-7\right)}{\displaystyle \lim_{n \rightarrow \infty}\left(1+\frac{3}{n^6}\right)}&\mbox{limit of a quotient is the quotient of the limits}\\
&=\displaystyle \frac{\displaystyle\lim_{n \rightarrow \infty} \frac{4}{n^6}-\lim_{n \rightarrow \infty}7}{\displaystyle \lim_{n \rightarrow \infty}1+\lim_{n \rightarrow \infty}\frac{3}{n^6}}&\mbox{limit of a sum/difference is the sum/difference of the limits}\\
&=\displaystyle \frac{0-7}{1+0}&\mbox{}\\
&=\displaystyle -7&\mbox{}\\
\end{array}
$$
Yes, the limit laws are awesome!
But the fish we'll be frying in this course will require dealing with trickier limits.
We're going to need a bit more machinery.
The next theorem is the first in the arsenal of tools we'll be forging in this section.
Big Gun #1: The Squeeze Theorem
Let $\{a_n\},$ $\{b_n\},$ and $\{c_n\}$ be sequences such that $a_n \leq b_n \leq c_n.$
If $\displaystyle \lim_{n \rightarrow \infty} a_n=\displaystyle \lim_{n \rightarrow \infty}c_n=L,$
then $\displaystyle \lim_{n \rightarrow \infty} b_n=L.$
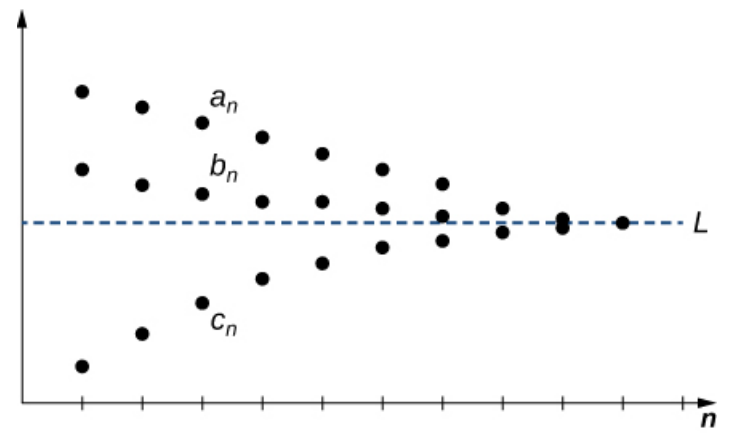

Examples: Squeeze Theorem
$\displaystyle \lim_{n \rightarrow \infty} (-1)^{n+1}\frac{1}{n}$
Since $$\displaystyle -\frac{1}{n} \leq (-1)^{n+1}\frac{1}{n} \leq \frac{1}{n},$$ and since
$$\displaystyle \lim_{n \rightarrow \infty} \left(-\frac{1}{n}\right)=0 \mbox{ and }\displaystyle \lim_{n \rightarrow \infty}\frac{1}{n}=0,$$
we may conclude by the Squeeze Theorem that
$$\displaystyle \lim_{n \rightarrow \infty} (-1)^{n+1}\frac{1}{n}=0$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{\cos n}{n}$
Since $$\displaystyle -\frac{1}{n} \leq \frac{\cos n}{n} \leq \frac{1}{n},$$ and since
$$\displaystyle \lim_{n \rightarrow \infty} \left(-\frac{1}{n}\right)=0 \mbox{ and }\displaystyle \lim_{n \rightarrow \infty}\frac{1}{n}=0,$$
we may conclude by the Squeeze Theorem that
$$\displaystyle \lim_{n \rightarrow \infty} \frac{\cos n}{n}=0$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{2n-\sin n}{n^2}$
We first note that since $$\displaystyle \frac{2n-1}{n^2} \leq \frac{2n-\sin n}{n^2} \leq \frac{2n+1}{n^2},$$ and since
$$\displaystyle \lim_{n \rightarrow \infty} \frac{2n-1}{n^2}=0 \mbox{ and }\displaystyle \lim_{n \rightarrow \infty}\frac{2n+1}{n^2}=0,$$
we may conclude by the Squeeze Theorem that
$$\displaystyle \lim_{n \rightarrow \infty} \frac{2n-\sin n}{n^2}=0$$
Continuous Functions and Sequences
Sequences and continuous functions get along very well together.
It's a love affair bridging the gap between the discrete and continuous worlds.
The following theorem bears witness to the above statement.
Big Gun #2: The Continuous Function Theorem for Sequences
Suppose $\displaystyle \lim_{n \rightarrow \infty} a_n=L$ and $f$ is a continuous function defined for all $a_n$ and is continuous at $L.$
Then $\displaystyle \lim_{n \rightarrow \infty} f(a_n)=f\left(\lim_{n \rightarrow \infty}a_n\right) =f(L).$
Examples: Use the Continuous Function Theorem for Sequences to find the following limits.
$\displaystyle \lim_{n \rightarrow \infty} \sqrt{\frac{n-1}{n}}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \sqrt{\frac{n-1}{n}}&=\displaystyle \sqrt{\lim_{n \rightarrow \infty}\frac{n-1}{n}}&\mbox{by the Continuous Function Theorem}\\
&=\displaystyle \sqrt{1}&\mbox{}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \cos \left(\frac{1}{n}\right)$
$$
\begin{array}{lll}
\displaystyle\lim_{n \rightarrow \infty} \cos \left(\frac{1}{n}\right)&=\displaystyle \cos \left(\lim_{n \rightarrow \infty} \frac{1}{n}\right)&\mbox{by the Continuous Function Theorem}\\
&=\displaystyle \cos \left(0\right)&\mbox{}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$
Another Handy Theorem
The next theorem allows us to use all of the machinery of functions we have spent the entire year building up to tell us about the long-term behavior of a sequence.
In particular, the next theorem will enable us to unleash L'Hôpital's Rule on sequences.
Big Gun #3: Limit of a Sequence Defined by a Function
If $\{a_n\}$ is a sequence such that $a_n=f(n),$ and if $\displaystyle \lim_{x \rightarrow \infty}f(x)=L,$ then $\displaystyle \lim_{n \rightarrow \infty} a_n=L.$
Using L'Hôpital's Rule: Find the limit of the following sequences.
$\displaystyle \lim_{n \rightarrow \infty}\frac{\ln n}{n}$
$$
\begin{array}{lll}
\displaystyle\lim_{n \rightarrow \infty}\frac{\ln n}{n}&=\displaystyle \lim_{n \rightarrow \infty}\frac{1/n}{1}&\mbox{by L'Hopital}\\
&=\displaystyle \frac{0}{1}&\mbox{}\\
&=\displaystyle 0&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \left(\frac{n+1}{n-1}\right)^n$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left(\frac{n+1}{n-1}\right)^n&=\displaystyle \lim_{n \rightarrow \infty} e^{\ln\left(\frac{n+1}{n-1}\right)^n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} e^{n\ln\left(\frac{n+1}{n-1}\right)}&\mbox{property of logs}\\
&=\displaystyle e^{\displaystyle \lim_{n \rightarrow \infty} n\ln\left(\frac{n+1}{n-1}\right)}&\mbox{by the Continuous Function Theorem}\\
\end{array}
$$
Thus, to find the original limit, we must find the new limit $\displaystyle \lim_{n \rightarrow \infty} n \ln \left( \frac{n+1}{n-1} \right).$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} n \ln \left( \frac{n+1}{n-1} \right)&=\displaystyle \lim_{n \rightarrow \infty} n \ln \left( 1+\frac{2}{n-1} \right)&\mbox{using polynomial long division}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{\ln \left( 1+\frac{2}{n-1} \right)}{1/n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{1/\left( 1+\frac{2}{n-1} \right)\frac{d}{dn}\left( 1+\frac{2}{n-1} \right)}{-1/n^2}&\mbox{using L'Hopital}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{1/\left( 1+\frac{2}{n-1} \right)\left(-\frac{2}{(n-1)^2} \right)}{-1/n^2}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{n^2\frac{2}{(n-1)^2}}{1+\frac{2}{n-1}}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{2\left(\frac{n}{n-1}\right)^2}{1+\frac{2}{n-1}}&\mbox{}\\
&=\displaystyle \frac{2}{1}&\mbox{}\\
&=\displaystyle 2&\mbox{}\\
\end{array}
$$
Finally, we may find the original limit.
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \left(\frac{n+1}{n-1}\right)^n&=\displaystyle e^{\displaystyle \lim_{n \rightarrow \infty} n\ln\left(\frac{n+1}{n-1}\right)}&\mbox{}\\
&=\displaystyle e^{2}&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty} \frac{2^n}{n^2}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty} \frac{2^n}{n^2}&=\displaystyle \lim_{n \rightarrow \infty} \frac{(\ln 2)2^n}{2n}&\mbox{using L'Hopital}\\
&=\displaystyle \lim_{n \rightarrow \infty} \frac{(\ln 2)(\ln 2) 2^n}{2}&\mbox{using L'Hopital again}\\
&=\displaystyle \infty&\mbox{}\\
\end{array}
$$
Some Common Limits
$\displaystyle \lim_{n \rightarrow \infty}\frac{\ln n}{n}=0$
$\displaystyle \lim_{n \rightarrow \infty} n^{1/n}=1$
$\displaystyle \lim_{n \rightarrow \infty} x^{1/n}=1$ for $x \gt 0$
$\displaystyle \lim_{n \rightarrow \infty} x^{n}=1$ for $|x| \lt 1$
$\displaystyle \lim_{n \rightarrow \infty} \left(1+\frac{x}{n}\right)^{n}=e^x$
$\displaystyle \lim_{n \rightarrow \infty} \frac{x^n}{n!}=0$ for any real number $x.$
More Examples
$\displaystyle \lim_{n \rightarrow \infty}\sqrt[n]{n^2}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty}\sqrt[n]{n^2}&=\displaystyle \lim_{n \rightarrow \infty}n^{2/n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left(n^{1/n}\right)^2&\mbox{}\\
&=\displaystyle \left(\lim_{n \rightarrow \infty} n^{1/n}\right)^2&\mbox{Continuous Function Theorem}\\
&=\displaystyle 1^2&\mbox{using common limits}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty}\sqrt[n]{3n}$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty}\sqrt[n]{3n}&=\displaystyle \lim_{n \rightarrow \infty}(3n)^{1/n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} 3^{1/n} n^{1/n}&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty} 3^{1/n} \lim_{n \rightarrow \infty} n^{1/n}&\mbox{}\\
&=\displaystyle 3^0\cdot 1&\mbox{Continuous Function Theorem and common limits }\\
&=\displaystyle 1\cdot 1&\mbox{}\\
&=\displaystyle 1&\mbox{}\\
\end{array}
$$
$\displaystyle \lim_{n \rightarrow \infty}\left(\frac{n-1}{n}\right)^n$
$$
\begin{array}{lll}
\displaystyle \lim_{n \rightarrow \infty}\left(\frac{n-1}{n}\right)^n&=\displaystyle \lim_{n \rightarrow \infty}\left(1-\frac{1}{n}\right)^n&\mbox{}\\
&=\displaystyle \lim_{n \rightarrow \infty}\left(1+\frac{(-1)}{n}\right)^n&\mbox{}\\
&=\displaystyle e^{-1}&\mbox{using common limits}\\
\end{array}
$$
Bounded Sequences
A sequence $\{a_n\}$ is bounded above if $a_{n+1}\leq M$ for some real number $M.$
A sequence $\{a_n\}$ is bounded below if $a_{n+1}\geq m$ for some real number $m.$
A sequence $\{a_n\}$ is bounded if it is bounded above and below.
A sequence $\{a_n\}$ is not bounded is called unbounded.
Basic Fact
Any convergent sequence $\{a_n\}$ is bounded.
Examples: Every convergent sequence we've seen so far! :P
Caution!
Although it may be true that any convergent sequence $\{a_n\}$ is bounded,
Not every bounded sequence is convergent!
Example: $a_n=(-1)^{n+1}$ is bounded, but not convergent.
Monotonic Sequences
A sequence $\{a_n\}$ is increasing if $a_{n+1}\geq a_n$ for all $n.$
A sequence $\{a_n\}$ is decreasing if $a_{n+1}\leq a_n$ for all $n.$
A sequence $\{a_n\}$ is monotone if it is either increasing or decreasing.
BIIIIG Gun #4: Monotone Convergence Theorem
Every bounded, monotone sequence $\{a_n\}$ is convergent.
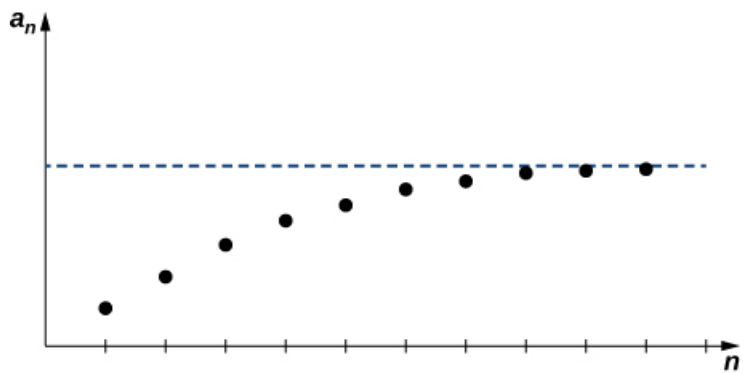
Example
Use the Monotone Convergence Theorem to show that the sequence $\displaystyle a_n=\frac{2^{n}}{n!}$ converges.
To apply the Monotone Convergence Theorem, we must show that
We not claim that $\{a_n\}$ is bounded above by $2.$ To see this we note that $$a_n=\frac{2^{n}}{n!}=\frac{2}{1}\cdot \frac{2}{2}\cdot \frac{2}{3}\cdots \frac{2}{n-1}\cdot \frac{2}{n}$$ We now show that $\{a_n\}$ is a strictly decreasing (monotone) sequence. $$ \begin{array}{lll} \displaystyle a_{n+1}&=\displaystyle \frac{2^{n+1}}{(n+1)!}&\mbox{}\\ &=\displaystyle \frac{2}{n+1}\frac{2^n}{n!}&\mbox{}\\ &\displaystyle \leq \frac{2^n}{n!}&\mbox{ since $\frac{2}{n+1} \leq 1$ for all $n\geq 1$}\\ &\displaystyle = a_n&\mbox{}\\ \end{array} $$ Thus, $\{a_n\}$ is monotone.
Since all the conditions of the Monotone Convergence Theorem have been met, we conclude that $\{a_n\}$ defined by $\displaystyle a_n=\frac{2^{n}}{n!}$ is a convergent sequence.
- $\{a_n\}$ is bounded below
- $\{a_n\}$ is bounded above
- $\{a_n\}$ is monotone
We not claim that $\{a_n\}$ is bounded above by $2.$ To see this we note that $$a_n=\frac{2^{n}}{n!}=\frac{2}{1}\cdot \frac{2}{2}\cdot \frac{2}{3}\cdots \frac{2}{n-1}\cdot \frac{2}{n}$$ We now show that $\{a_n\}$ is a strictly decreasing (monotone) sequence. $$ \begin{array}{lll} \displaystyle a_{n+1}&=\displaystyle \frac{2^{n+1}}{(n+1)!}&\mbox{}\\ &=\displaystyle \frac{2}{n+1}\frac{2^n}{n!}&\mbox{}\\ &\displaystyle \leq \frac{2^n}{n!}&\mbox{ since $\frac{2}{n+1} \leq 1$ for all $n\geq 1$}\\ &\displaystyle = a_n&\mbox{}\\ \end{array} $$ Thus, $\{a_n\}$ is monotone.
Since all the conditions of the Monotone Convergence Theorem have been met, we conclude that $\{a_n\}$ defined by $\displaystyle a_n=\frac{2^{n}}{n!}$ is a convergent sequence.
Caution!
Although it may be true that very bounded, monotone sequence $\{a_n\}$ is convergent,
Not every convergent sequence is monotonic!
Example: $\displaystyle a_n=(-1)^{n+1}\frac{1}{n}$ is convergent, but not monotone.
Bonus Example: The Logistic Map
Initial value: $x_1=$. Parameter: $r=$. $$x_{n+1}=rx_n(1-x_n)$$
| $x_n$ | |||
| $n$ |
The Logistic Map Bifurcation Diagram
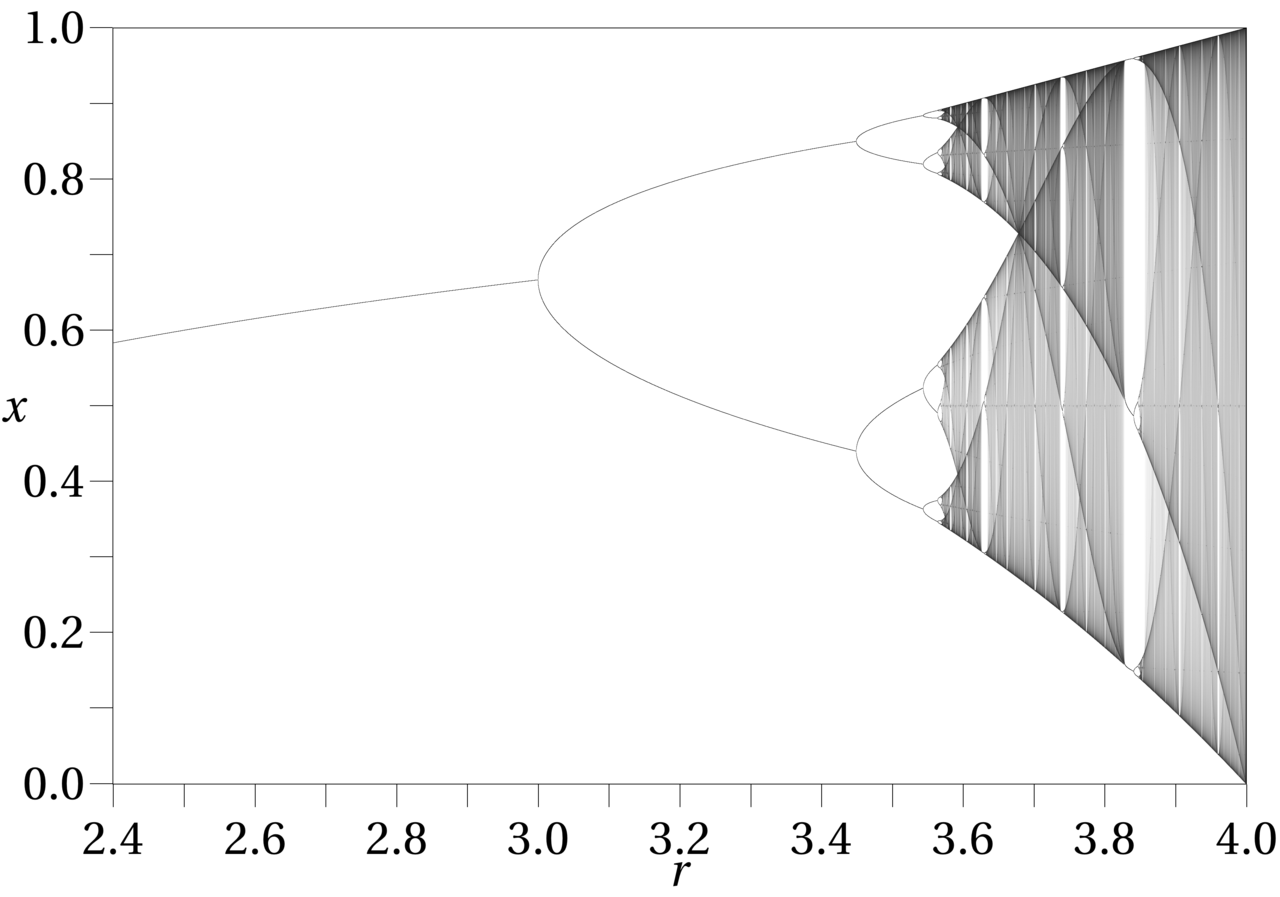
Bonus Example: The Logistic Map and Chaos
Initial value: $x_1=$. Parameter: $r=$. $$x_{n+1}=rx_n(1-x_n)$$
| $x_n$ |  | ||
| $n$ |