An equation involving an unknown function and its derivatives is known as a differential equation.
As we shall see, differential equations appear in a diversity of disciplines! From physics, to chemistry, biology, epidemiology, psychology, sociology (the spread of information).
Examples of Differential Equations
$\displaystyle \frac{d^2s}{dt^2}=-g,$ free fall under influence gravity alone
$\displaystyle m\frac{dv}{dt}=-kv-mg,$ free fall under influence gravity with air resistance
$\displaystyle \frac{dT}{dt}=k(T-T_a),$ Newton's Law of Cooling
$\displaystyle \frac{dP}{dt}=kP,$ uninhibited population growth (Malthusian growth)
$\displaystyle \frac{dP}{dt}=kP\left(1-\frac{P}{K}\right),$ limited population growth (logistic growth)
More Examples of Differential Equations!
$\displaystyle \frac{d^2\theta}{dt^2}+\frac{g}{L}\sin \theta=0$ model for the motion of a simple pendulum
$\displaystyle Rq'+\frac{1}{C}q=E,$ charge on a capacitor in an $RC$ circuit
$\displaystyle LI'+RI=E,$ the amount of current in an $LR$ circuit
$\displaystyle -\frac{d[A]}{dt}=k[A]^n,$ equation describing the concentration of of a reactant in an $n$th order reaction
$\displaystyle \frac{dp}{dS}=\frac{k}{S},$ Weber-Fechner law: perceived sensation is proportional to logarithm of the actual intensity
$\displaystyle \frac{dS}{dt}=-\frac{\beta IS}{N},$ $\displaystyle \frac{dI}{dt}=\frac{\beta IS}{N}-\gamma I,$ $\displaystyle \frac{dR}{dt}=\gamma I,$ SIR model from epidemiology
Separable Differential Equations
A separable differential equation is an equation that can be written in the form $$\frac{dy}{dx}=f(x)g(y).$$
Examples: Separable Differential Equations
$y'=e^yx^2$
First we write the equation in differential form to separate variables.
$$
\frac{dy}{dx}=e^yx^2
$$
Then
$$
e^{-y}\,dy=x^2\,dx
$$
Integrating both sides
$$
\int e^{-y}\,dy=\int x^2\,dx
$$
Then
$$
\begin{array}{lll}
&\displaystyle -e^{-y}+C_1=\frac{1}{3}x^3+C_2&\\
\implies &\displaystyle -e^{-y}=\frac{1}{3}x^3+C_2-C_1&\\
\implies &\displaystyle -e^{-y}=\frac{1}{3}x^3+C_3&\mbox{ renaming the constant}\\
\implies &\displaystyle e^{-y}=-\frac{1}{3}x^3-C_3&\mbox{}\\
\implies &\displaystyle e^{-y}=-\frac{1}{3}x^3+C_4&\mbox{renaming the constant again}\\
\implies &\displaystyle -y=\ln\left(-\frac{1}{3}x^3+C_4\right)&\mbox{}\\
\implies &\displaystyle y=-\ln\left(-\frac{1}{3}x^3+C_4\right)&\mbox{}\\
\end{array}
$$
We could also write the above in other forms
$$
y=\ln\left(\frac{1}{-\frac{1}{3}x^3+C_4}\right)=\ln\left(\frac{3}{C-x^3}\right)
$$
renaming the constant one last time.
We now verify that the above is indeed the general solution of the differential equation. $$ \begin{array}{lll} \displaystyle \frac{dy}{dx} &=\displaystyle \frac{d}{dx}\ln\left(\frac{3}{C-x^3}\right)&\mbox{}\\ &=\displaystyle \frac{1}{\frac{3}{C-x^3}}\frac{d}{dx}\frac{3}{C-x^3}&\mbox{}\\ &=\displaystyle \frac{C-x^3}{3}\frac{d}{dx}\left(3(C-x^3)^{-1}\right)&\mbox{}\\ &=\displaystyle \frac{C-x^3}{3}\left(-3(C-x^3)^{-2}\right)\frac{d}{dx}(C-x^3)&\mbox{}\\ &=\displaystyle -\frac{1}{C-x^3}(-3x^2)&\mbox{}\\ &=\displaystyle \frac{3}{C-x^3}x^2&\mbox{}\\ &=\displaystyle e^{\ln\left(\frac{3}{C-x^3}\right)}x^2&\mbox{}\\ &=\displaystyle e^{y}x^2&\mbox{}\\ \end{array} $$
We now verify that the above is indeed the general solution of the differential equation. $$ \begin{array}{lll} \displaystyle \frac{dy}{dx} &=\displaystyle \frac{d}{dx}\ln\left(\frac{3}{C-x^3}\right)&\mbox{}\\ &=\displaystyle \frac{1}{\frac{3}{C-x^3}}\frac{d}{dx}\frac{3}{C-x^3}&\mbox{}\\ &=\displaystyle \frac{C-x^3}{3}\frac{d}{dx}\left(3(C-x^3)^{-1}\right)&\mbox{}\\ &=\displaystyle \frac{C-x^3}{3}\left(-3(C-x^3)^{-2}\right)\frac{d}{dx}(C-x^3)&\mbox{}\\ &=\displaystyle -\frac{1}{C-x^3}(-3x^2)&\mbox{}\\ &=\displaystyle \frac{3}{C-x^3}x^2&\mbox{}\\ &=\displaystyle e^{\ln\left(\frac{3}{C-x^3}\right)}x^2&\mbox{}\\ &=\displaystyle e^{y}x^2&\mbox{}\\ \end{array} $$
$(1 + x)y' = (x + 2)(y - 1)$
Rewriting the equation in differential form,
$$(1 + x)\frac{dy}{dx} = (x + 2)(y - 1)$$
Then
$$
\frac{dy}{y-1}=\frac{x+2}{x+1}\,dx
$$
Integrating, we get
$$
\int \frac{dy}{y-1}=\int \frac{x+2}{x+1}\,dx
$$
Using polynomial long division we rewrite the integrand $\displaystyle \frac{x+2}{x+1}$ as $\displaystyle 1+\frac{1}{x+1}.$
Then the above becomes
$$ \int \frac{dy}{y-1}=\int 1+\frac{1}{x+1}\,dx $$ and we have $$ \ln|y-1|=x+\ln|x+1|+C $$ Public Service Announcement: This time, instead of all that $C_1,$ $C_2,$ and "constant-renaming" business, we're going to let $C$ stand for THE constant, even if it does feel a little strange algebraically. The thing to keep in mind is that when we write $+C,$ we're talking about an entire family of curves. For example, $y=f(x)+3C$ is the same solution set as $y=f(x)+C.$ We say the $3$ is "absorbed into the constant."
The above then becomes $$ |y-1|=e^{x+\ln|x+1|+C} $$ or, $$ |y-1|=e^{x+\ln|x+1|}e^C $$ Then, $$ |y-1|=Ce^{x+\ln|x+1|} $$ rewriting $e^C$ as $C$ since it is a constant. The above gives $$ y-1=\pm Ce^{x+\ln|x+1|} $$ so that $$ y-1=Ce^{x+\ln|x+1|} $$ absorbing the $\pm$ into the constant. Finally, $$ y=Ce^{x+\ln|x+1|}+1 $$ Verifying our solution, we start at the left-hand side and work our way to the right-hand side. $$ \begin{array}{lll} \displaystyle (1+x)y' &\displaystyle (1+x)\frac{dy}{dx}\\ &=\displaystyle (1+x)\frac{d}{dx}\left(Ce^{x+\ln|x+1|}+1\right)&\mbox{}\\ &=\displaystyle (1+x)\left(Ce^{x+\ln|x+1|}\right)\frac{d}{dx}\left(x+\ln|x+1|\right)&\mbox{}\\ &=\displaystyle (1+x)\left(Ce^{x+\ln|x+1|}\right)\left(1+\frac{1}{x+1}\right)&\mbox{}\\ &=\displaystyle (1+x)\left(1+\frac{1}{x+1}\right)\left(Ce^{x+\ln|x+1|}\right)&\mbox{}\\ &=\displaystyle \left(1+x+1\right)\left(Ce^{x+\ln|x+1|}+1-1\right)&\mbox{}\\ &=\displaystyle \left(x+2\right)\left(y-1\right)&\mbox{}\\ \end{array} $$
$$ \int \frac{dy}{y-1}=\int 1+\frac{1}{x+1}\,dx $$ and we have $$ \ln|y-1|=x+\ln|x+1|+C $$ Public Service Announcement: This time, instead of all that $C_1,$ $C_2,$ and "constant-renaming" business, we're going to let $C$ stand for THE constant, even if it does feel a little strange algebraically. The thing to keep in mind is that when we write $+C,$ we're talking about an entire family of curves. For example, $y=f(x)+3C$ is the same solution set as $y=f(x)+C.$ We say the $3$ is "absorbed into the constant."
The above then becomes $$ |y-1|=e^{x+\ln|x+1|+C} $$ or, $$ |y-1|=e^{x+\ln|x+1|}e^C $$ Then, $$ |y-1|=Ce^{x+\ln|x+1|} $$ rewriting $e^C$ as $C$ since it is a constant. The above gives $$ y-1=\pm Ce^{x+\ln|x+1|} $$ so that $$ y-1=Ce^{x+\ln|x+1|} $$ absorbing the $\pm$ into the constant. Finally, $$ y=Ce^{x+\ln|x+1|}+1 $$ Verifying our solution, we start at the left-hand side and work our way to the right-hand side. $$ \begin{array}{lll} \displaystyle (1+x)y' &\displaystyle (1+x)\frac{dy}{dx}\\ &=\displaystyle (1+x)\frac{d}{dx}\left(Ce^{x+\ln|x+1|}+1\right)&\mbox{}\\ &=\displaystyle (1+x)\left(Ce^{x+\ln|x+1|}\right)\frac{d}{dx}\left(x+\ln|x+1|\right)&\mbox{}\\ &=\displaystyle (1+x)\left(Ce^{x+\ln|x+1|}\right)\left(1+\frac{1}{x+1}\right)&\mbox{}\\ &=\displaystyle (1+x)\left(1+\frac{1}{x+1}\right)\left(Ce^{x+\ln|x+1|}\right)&\mbox{}\\ &=\displaystyle \left(1+x+1\right)\left(Ce^{x+\ln|x+1|}+1-1\right)&\mbox{}\\ &=\displaystyle \left(x+2\right)\left(y-1\right)&\mbox{}\\ \end{array} $$
Fun Fact
Every time we found an indefinite integral $\displaystyle \int f(x) \, dx,$ we were solving the basic (separable!) differential equation $$\frac{dy}{dx}=f(x).$$
For example, $\displaystyle \int 2x \, dx=x^2+C$ is the general solution to $\displaystyle \frac{dy}{dx}=2x.$
Initial Value Problems
We have seen, the solution to $y'=e^yx^2$ is a family of curves.
In applications, we very often are interested in a particular solution which is specified by an initial condition.
An initial condition usually has the form $y(x_0)=y_0$ where $x_0$ and $y_0$ are specified values.
For example, we could stipulate that $y(0)=1$ for a solution to the above equation.
A differential equation with an initial condition is called an initial value problem.
Example
Solve the initial value problem $$ y'=e^yx^2\\ y(0)=1. $$
From our first example, the general solution is
$$
y=\ln\left(\frac{3}{C-x^3}\right)
$$
Imposing the initial condition $y(0)=1$ gives
$$
\begin{array}{lrll}
&\displaystyle y(0)&=1 &\mbox{}\\
\implies &\displaystyle \ln\left(\frac{3}{C-0^3}\right)&=\displaystyle 1&\mbox{}\\
\implies &\displaystyle \ln\left(\frac{3}{C}\right)&=\displaystyle 1&\mbox{}\\
\implies &\displaystyle \frac{3}{C}&=\displaystyle e^1=e&\mbox{}\\
\implies &\displaystyle C&=\displaystyle \frac{3}{e}\approx 1.103638324&\mbox{}\\
\end{array}
$$
Thus,
$$
y=\ln\left(\frac{3}{\frac{3}{e}-x^3}\right)
$$
solves the initial value problem.
Application: Chemistry
A first-order reaction of depends on the concentration $[A]$ of a single reactant and obeys the differential equation $$ -\frac{d[A]}{dt}=k[A] $$ where $k$ is the rate constant of the reaction.
Sulfuryl chloride, $\mbox{SO}_2\mbox{Cl}_2$ decomposes into sulfur dioxide and chlorine gas according to the first-order reaction $$\mbox{SO}_2\mbox{Cl}_2\rightarrow \mbox{SO}_2 + \mbox{Cl}_2.$$ At $320^{\circ}\mbox{C}$ the rate constant is $0.000022$ $\mbox{s}^{-1}.$
If the initial concentration of sulfuryl chloride is $0.008 \mbox{ M},$ what is the concentration after $1$ hour?
Letting $[A]$ represent the concentration of $\mbox{SO}_2\mbox{Cl}_2$ in $\mbox{M},$ the problem we want to solve
is nothing more than an initial value problem.
$$
-\frac{d[A]}{dt}=0.000022[A]\\
[A](0)=0.008
$$
First we find the general solution to $\displaystyle -\frac{d[A]}{dt}=k[A].$
$$
\begin{array}{llll}
&\displaystyle -\frac{d[A]}{dt}=0.000022[A]&\displaystyle &\mbox{}\\
\implies &\displaystyle \frac{d[A]}{[A]}=-0.000022\,dt&\displaystyle &\mbox{separating variables}\\
\implies &\displaystyle \int \frac{d[A]}{[A]}=-0.000022\int \,dt&\displaystyle &\mbox{integrating both sides}\\
\implies &\displaystyle \ln [A]=-0.000022t+C&\displaystyle &\mbox{}\\
\implies &\displaystyle [A]=e^{-0.000022t+C}&\displaystyle &\mbox{}\\
\implies &\displaystyle [A]=e^{-0.000022t}e^{C}&\displaystyle &\mbox{}\\
\implies &\displaystyle [A]=Ce^{-0.000022t}&\displaystyle &\mbox{$e^C$ is just a constant}\\
\end{array}
$$
Imposing the initial condition, we get a particular solution.
$$
\begin{array}{llll}
&\displaystyle [A](0)&=0.008 &\mbox{}\\
\implies &\displaystyle Ce^{-0.000022\cdot 0}&=\displaystyle 0.008&\mbox{}\\
\implies &\displaystyle Ce^{0}&=\displaystyle 0.008&\mbox{}\\
\implies &\displaystyle C&=\displaystyle 0.008&\mbox{}\\
\end{array}
$$
Thus,
$$
[A](t)=0.008e^{-0.000022t}.
$$
So, after $1$ hour, or $3600$ seconds, the concentration of sulfuryl chloride will be $[A](3600)=e^{-0.000022 \cdot 3600}\approx 0.00739$ $\mbox{M}.$
Application: Newton's Law of Cooling
You have a fresh, piping hot $300$ ml cup of coffee at temperature $100^{\circ}$C that you put outside, where the ambient temperature is $20^{\circ}$C. Assuming a cooling constant $k=-0.0447,$
What will the temperature of the coffee be after $10$ minutes?
After how many minutes will the temperature be $60$ degrees Celsius?

Newton's law of cooling is $\displaystyle \frac{dT}{dt}=k(T-T_a),$ where $T_a$ is the ambient temperature.
The problem statement gives us the initial temperature, $T(0)=100,$ the ambient temperature of $T=20,$ and the cooling constant $k=-0.0447.$
Thus, the initial value problem to solve is $$ \frac{dT}{dt}=-0.0447(T-20)\\ T(0)=100 $$ To find the general solution, we separate variables. $$ \begin{array}{ll} &\displaystyle \frac{dT}{T-20}=-0.0447\,dt\\ \implies &\displaystyle \int \frac{dT}{T-20}=-0.0447\int \,dt\\ \implies & \ln|T-20|=-0.0447t+C\\ \implies & |T-20|=e^{-0.0447t+C}\\ \implies & |T-20|=e^{-0.0447t}e^{C}\\ \implies & |T-20|=Ce^{-0.0447t}\\ \end{array} $$ Since the temperature is greater than the ambient temperature, $T-20=Ce^{-0.0447t}$ so that our general solution is $$ T=Ce^{-0.0447t}+20 $$ We now satisfy the initial condition to find $C.$ Since $T(0)=100,$ $$ \begin{array}{ll} &T(0)=Ce^{-0.0447\cdot 0}+20\\ \implies &100=C+20\\ \implies &C=80\\ \end{array} $$ Thus, our particular solution is $$ T=80e^{-0.0447t}+20 $$ To answer the first question, $$T(10)=80e^{-0.0447\cdot 10}+20\approx 71.16351266$$ That is, the temperature of the coffee after $10$ minutes will be approximately $71.2$ degrees Celsius.
To answer the second question, we set $T=60$ and solve for $t.$ $$ \begin{array}{ll} & T=60\\ \implies & \displaystyle 80e^{-0.0447t}+20=60\\ \implies & \displaystyle 80e^{-0.0447t}=40\\ \implies & \displaystyle e^{-0.0447t}=\frac{1}{2}\\ \implies & \displaystyle -0.0447t=\ln\left(\frac{1}{2}\right)\\ \implies & \displaystyle t=-\frac{\ln\left(\frac{1}{2}\right)}{0.0447}\approx 15.50664833\\ \end{array} $$ That is, the temperature of the coffee will be $60$ degrees Celsius after approximately $15.5$ minutes.
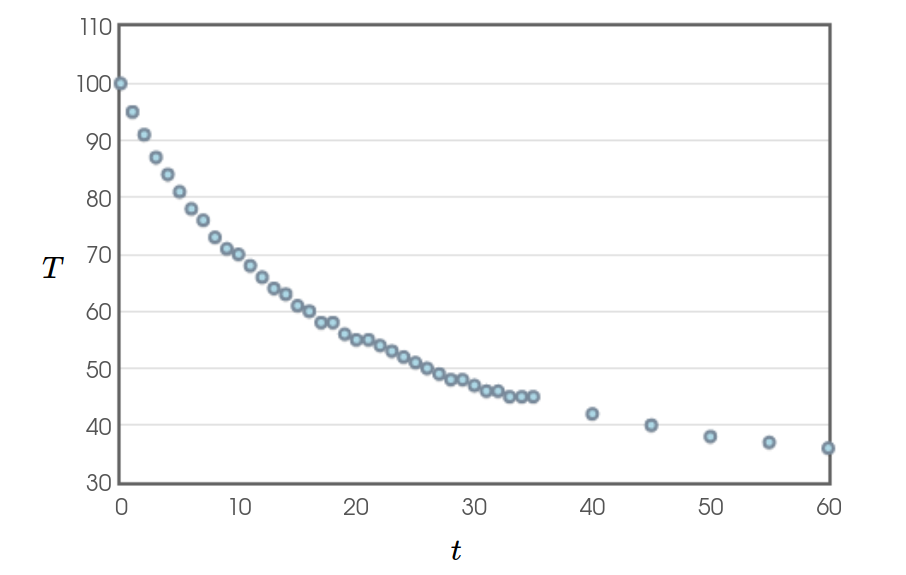
Below is a graph of some temperature and time data for a $300 \mbox{ mL}$ beaker of water under the same conditions as our coffee.
The problem statement gives us the initial temperature, $T(0)=100,$ the ambient temperature of $T=20,$ and the cooling constant $k=-0.0447.$
Thus, the initial value problem to solve is $$ \frac{dT}{dt}=-0.0447(T-20)\\ T(0)=100 $$ To find the general solution, we separate variables. $$ \begin{array}{ll} &\displaystyle \frac{dT}{T-20}=-0.0447\,dt\\ \implies &\displaystyle \int \frac{dT}{T-20}=-0.0447\int \,dt\\ \implies & \ln|T-20|=-0.0447t+C\\ \implies & |T-20|=e^{-0.0447t+C}\\ \implies & |T-20|=e^{-0.0447t}e^{C}\\ \implies & |T-20|=Ce^{-0.0447t}\\ \end{array} $$ Since the temperature is greater than the ambient temperature, $T-20=Ce^{-0.0447t}$ so that our general solution is $$ T=Ce^{-0.0447t}+20 $$ We now satisfy the initial condition to find $C.$ Since $T(0)=100,$ $$ \begin{array}{ll} &T(0)=Ce^{-0.0447\cdot 0}+20\\ \implies &100=C+20\\ \implies &C=80\\ \end{array} $$ Thus, our particular solution is $$ T=80e^{-0.0447t}+20 $$ To answer the first question, $$T(10)=80e^{-0.0447\cdot 10}+20\approx 71.16351266$$ That is, the temperature of the coffee after $10$ minutes will be approximately $71.2$ degrees Celsius.
To answer the second question, we set $T=60$ and solve for $t.$ $$ \begin{array}{ll} & T=60\\ \implies & \displaystyle 80e^{-0.0447t}+20=60\\ \implies & \displaystyle 80e^{-0.0447t}=40\\ \implies & \displaystyle e^{-0.0447t}=\frac{1}{2}\\ \implies & \displaystyle -0.0447t=\ln\left(\frac{1}{2}\right)\\ \implies & \displaystyle t=-\frac{\ln\left(\frac{1}{2}\right)}{0.0447}\approx 15.50664833\\ \end{array} $$ That is, the temperature of the coffee will be $60$ degrees Celsius after approximately $15.5$ minutes.
Below is a graph of some temperature and time data for a $300 \mbox{ mL}$ beaker of water under the same conditions as our coffee.

Application: Mixture Problem
A tank contains $50 \mbox{ kg}$ of salt dissolved in $5000 \mbox{ L}$ of water. A salt solution of $0.02 \mbox{ kg}$ salt per liter is pumped into the tank at a rate of $125$ liters per minute and is drained at the same rate. Solve for the salt concentration at time $t.$ Assume the tank is always being stirred and is well mixed.
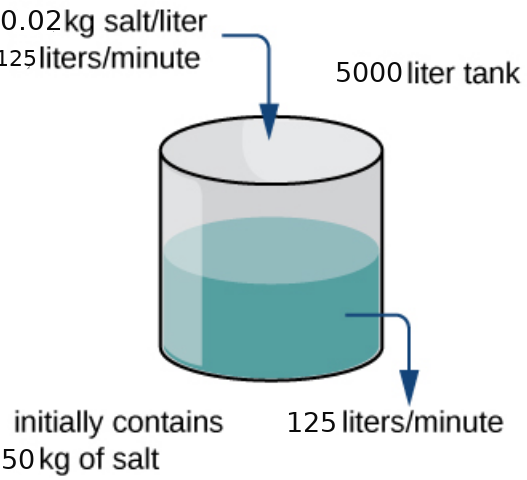
Let $A(t)$ be the amount of salt in the tank at time $t.$
The overall rate at which the salt is changing can be determined by the rate at which salt is entering the tank and the rate at which it is leaving the tank. That is, $$ \frac{dA}{dt}=\mbox{Rate Salt Enters Tank}-\mbox{Rate Salt Leaves Tank}. $$ Rate Salt Enters Tank: The solution enters the tank at a rate of $125 \frac{\mbox{L}}{\mbox{min}},$ and since the concentration is $0.02 \frac{\mbox{kg}}{\mbox{L}},$ the rate at which the salt is entering the tank is $$ \mbox{Rate Salt Enters Tank}=125 \frac{\mbox{L}}{\mbox{min}} \cdot 0.02 \frac{\mbox{kg}}{\mbox{L}}=2.5 \frac{\mbox{kg}}{\mbox{min}} $$ Rate Salt Leaves Tank: The solution is also draining at a rate of $125 \frac{\mbox{L}}{\mbox{min}}.$ Since the total amount salt in the tank $A(t)$ is changing at every moment $t,$ the concentration of salt in the tank also depends on time. The concentration at time $t$ is $\displaystyle \frac{A(t) \mbox{ kg}}{5000 \mbox{ L}}.$ $$ \mbox{Rate Salt Leaves Tank}=125 \frac{\mbox{L}}{\mbox{min}} \cdot \frac{A(t) \mbox{ kg}}{5000 \mbox{ L}}=0.025A(t)\frac{\mbox{kg}}{\mbox{min}} $$ Thus, the differential equation which $A(t)$ satisfies is $$ \frac{dA}{dt}=2.5-0.025A $$ For the general solution we separate variables. $$ \begin{array}{ll} &\displaystyle \frac{dA}{2.5-0.025A}=\,dt\\ \implies &\displaystyle 40\frac{dA}{100-A}=\,dt\\ \implies &\displaystyle 40\int \frac{dA}{100-A}=\int \,dt\\ \implies &\displaystyle -40\ln|100-A|=t+C\\ \implies &\displaystyle \ln|100-A|=-\frac{t}{40}+C\\ \implies &\displaystyle |100-A|=e^{-\frac{t}{40}+C}\\ \implies &\displaystyle |100-A|=e^{-\frac{t}{40}}e^{C}\\ \implies &\displaystyle |100-A|=Ce^{-\frac{t}{40}}\\ \implies &\displaystyle 100-A=\pm Ce^{-\frac{t}{40}}\\ \implies &\displaystyle A-100=Ce^{-\frac{t}{40}}\\ \implies &\displaystyle A=Ce^{-\frac{t}{40}}+100\\ \end{array} $$ Since there are $50 \mbox{ kg}$ of salt to start with in the tank, our initial condition is $A(0)=50.$ Thus, $$ \begin{array}{ll} &A(0)=Ce^{-\frac{0}{40}}+100\\ \implies &50=C+100\\ \implies &C=-50\\ \end{array} $$ The particular solution is then $$ A(t)=-50e^{-\frac{t}{40}}+100 $$ A graph of this solution is given below.
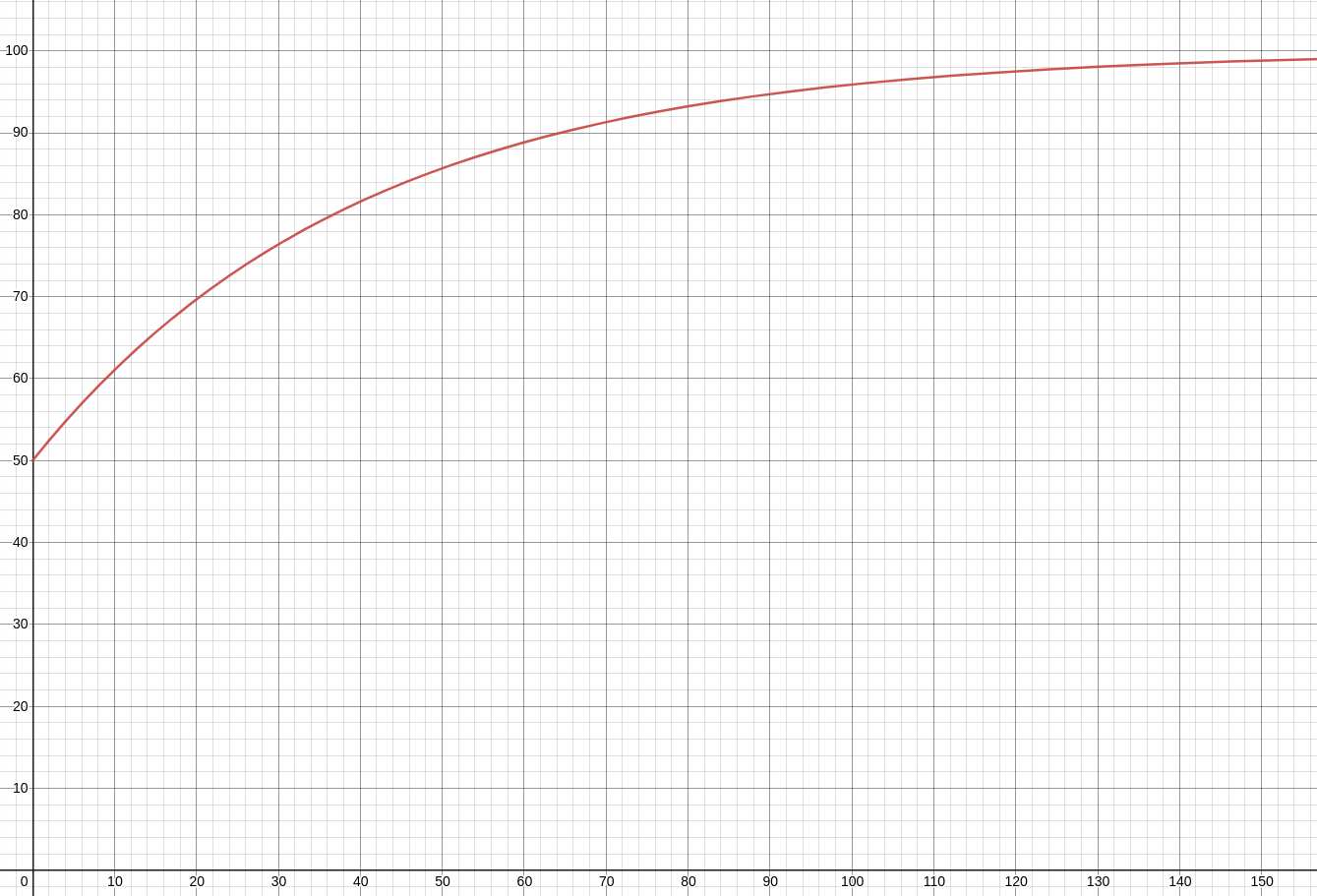
The overall rate at which the salt is changing can be determined by the rate at which salt is entering the tank and the rate at which it is leaving the tank. That is, $$ \frac{dA}{dt}=\mbox{Rate Salt Enters Tank}-\mbox{Rate Salt Leaves Tank}. $$ Rate Salt Enters Tank: The solution enters the tank at a rate of $125 \frac{\mbox{L}}{\mbox{min}},$ and since the concentration is $0.02 \frac{\mbox{kg}}{\mbox{L}},$ the rate at which the salt is entering the tank is $$ \mbox{Rate Salt Enters Tank}=125 \frac{\mbox{L}}{\mbox{min}} \cdot 0.02 \frac{\mbox{kg}}{\mbox{L}}=2.5 \frac{\mbox{kg}}{\mbox{min}} $$ Rate Salt Leaves Tank: The solution is also draining at a rate of $125 \frac{\mbox{L}}{\mbox{min}}.$ Since the total amount salt in the tank $A(t)$ is changing at every moment $t,$ the concentration of salt in the tank also depends on time. The concentration at time $t$ is $\displaystyle \frac{A(t) \mbox{ kg}}{5000 \mbox{ L}}.$ $$ \mbox{Rate Salt Leaves Tank}=125 \frac{\mbox{L}}{\mbox{min}} \cdot \frac{A(t) \mbox{ kg}}{5000 \mbox{ L}}=0.025A(t)\frac{\mbox{kg}}{\mbox{min}} $$ Thus, the differential equation which $A(t)$ satisfies is $$ \frac{dA}{dt}=2.5-0.025A $$ For the general solution we separate variables. $$ \begin{array}{ll} &\displaystyle \frac{dA}{2.5-0.025A}=\,dt\\ \implies &\displaystyle 40\frac{dA}{100-A}=\,dt\\ \implies &\displaystyle 40\int \frac{dA}{100-A}=\int \,dt\\ \implies &\displaystyle -40\ln|100-A|=t+C\\ \implies &\displaystyle \ln|100-A|=-\frac{t}{40}+C\\ \implies &\displaystyle |100-A|=e^{-\frac{t}{40}+C}\\ \implies &\displaystyle |100-A|=e^{-\frac{t}{40}}e^{C}\\ \implies &\displaystyle |100-A|=Ce^{-\frac{t}{40}}\\ \implies &\displaystyle 100-A=\pm Ce^{-\frac{t}{40}}\\ \implies &\displaystyle A-100=Ce^{-\frac{t}{40}}\\ \implies &\displaystyle A=Ce^{-\frac{t}{40}}+100\\ \end{array} $$ Since there are $50 \mbox{ kg}$ of salt to start with in the tank, our initial condition is $A(0)=50.$ Thus, $$ \begin{array}{ll} &A(0)=Ce^{-\frac{0}{40}}+100\\ \implies &50=C+100\\ \implies &C=-50\\ \end{array} $$ The particular solution is then $$ A(t)=-50e^{-\frac{t}{40}}+100 $$ A graph of this solution is given below.

Mixture Problem Redux
A trauma patient losing blood at a rate of $125 \frac{\mbox{mL}}{\mbox{hr}}$ has just arrived at the hospital. Paramedics inform the emergency room staff that the patient presently has $50 \mbox{ mg}$ of a life-saving drug in the bloodstream and they have maintained $5000 \mbox{ mL}$ of blood (a typical volume of blood in the human body).
To replace the lost blood, the emergency staff begin a blood transfusion of $125 \frac{\mbox{mL}}{\mbox{hr}}$ along with an IV drip of the life-saving drug at a concentration of $0.02 \mbox{ mg}$ per milliliter.
If the patient continues losing blood at the same rate, solve for the amount of the drug in the patient's blood stream at time $t.$
$$
A(t)=-50e^{-\frac{t}{40}}+100
$$
Look no further than the previous example!
Some Other Examples of Mixture Problems
Pollution level of a lake with polluted water entering and draining via rivers.
Population level with individuals entering the population (birth) and leaving the population (death).
Cash flow into an out of a financial institution.
Other Models Involving Separable Differential Equations
$\displaystyle \frac{dP}{dt}=kP,$ uninhibited population growth (Malthusian growth)
$\displaystyle \frac{dP}{dt}=kP\left(1-\frac{P}{K}\right),$ limited population growth (logistic growth)
$\displaystyle \frac{dP}{dt}=k(M-P),$ a model for learning where $P$ is a learning curve.
$\displaystyle \frac{dp}{dS}=\frac{k}{S},$ Weber-Fechner law: perceived sensation is proportional to logarithm of the actual intensity
STOP TAKING NOTES NOW!!!
Bonus Example: The SIR Model
Below you will find an implementation of the SIR model which is a differential-equation model of the spread of disease in a population. The model separates the population into three groups: susceptible, infectious, and recovered (hence, the model's name, SIR). The dynamics are determined by two numbers: $R_0,$ or the basic reproduction number, and the duration, $D,$ an infectious person can spread the disease. $R_0$ is a unit-less number and is interpreted as the average number of susceptible individuals one case can infect; it is a measure of how easily the disease spreads. $R_0$ depends on population behaviors such as social distancing and hygienic practice. By lowering $R_0$ you can flatten the (infectious) curve!
$$ \begin{array}{l} \displaystyle \frac{dS}{dt}=-\frac{\beta IS}{N},\,\,\,\,\,\,\,\, \\ \displaystyle \frac{dI}{dt}=\frac{\beta IS}{N}-\gamma I,\,\,\,\,\,\,\,\, \\ \displaystyle \frac{dR}{dt}=\gamma I \end{array} $$
$\displaystyle N=328.2$ million (the present U.S. population),
$\displaystyle I_0=1$ case (1st U.S. Case confirmed January 21st. 2020)
$\displaystyle R_0=\frac{\beta}{\gamma}=$, $\displaystyle D=\frac{1}{\gamma}=$ days (duration of infection still unclear)
$\displaystyle R_0=\frac{\beta}{\gamma}=$, $\displaystyle D=\frac{1}{\gamma}=$ days (duration of infection still unclear)
| Susceptible | Infectious | Recovered |
| Time in Days | Time in Days | Time in Days |