The Big Idea
A probability is a long term proportion of a particular outcome.
Example: Toss a coin. What is the probability of getting heads or tails?
Long-Term Proportion of Heads
| Empirical Probability | |||
| Number of Flips |
Example: Roll a pair of dice and take the sum of their faces. What is the probability of rolling a sum of $3?$
Below is a table of all possible rolls.

Probability Vocab
The sample space $S$ of a random phenomenon is the set of all possible outcomes.
An event is an outcome or a set of outcomes of a random phenomenon. That is, an event is a subset of the sample space.
A probability model is a mathematical description of a random phenomenon consisting of two parts: a sample space $S$ and a way of assigning probabilities to events.
The Classical Definition of Probability
Let $A$ be an event in the sample space $S.$ Then $$P(A)=\frac{n(A)}{n(S)}=\frac{\mbox{# ways $A$ can occur}}{\mbox{# of possible outcomes}}.$$
Example: Flip a coin.
The sample space is $S=\{\mbox{Heads},\mbox{Tails}\}.$ The event "heads" which we shall call $H$ is the subset of $S$ given by $H=\{\mbox{Heads}\}.$
Therefore, the classical probability of heads is given by $$P(H)=\frac{n(H)}{n(S)}=\frac{\mbox{# ways heads can occur}}{\mbox{# of possible outcomes}}=\frac{1}{2}.$$
For the dice pair rolling example, the sample space $S$ is the collections of all possible rolls:

$\{$
 $,$
$,$
 $\}$
$\}$
 $,$
$,$
 $\}$
$\}$
Example: Rolling a Sum of $3$
The event "roll a sum of $3$" which we shall call $A$ is the subset of $S$ given
Therefore, the classical probability of "rolling a sum of 3" is given by $$P(A)=\frac{n(A)}{n(S)}=\frac{\mbox{2 possible sums of 3}}{\mbox{36 possible outcomes}}=\frac{1}{18}.$$
The entire probability model for the dice pair example is.
$$ \begin{array}{c} P(\mbox{rolling a sum of 2})=1/36\\ P(\mbox{rolling a sum of 3})=2/36\\ P(\mbox{rolling a sum of 4})=3/36\\ P(\mbox{rolling a sum of 5})=4/36\\ P(\mbox{rolling a sum of 6})=5/36\\ P(\mbox{rolling a sum of 7})=6/36\\ P(\mbox{rolling a sum of 8})=5/36\\ P(\mbox{rolling a sum of 9})=4/36\\ P(\mbox{rolling a sum of 10})=3/36\\ P(\mbox{rolling a sum of 11})=2/36\\ P(\mbox{rolling a sum of 12})=1/36\\ \end{array} $$
Exercise: Let roll a pair of dice and see for ourselves how often we "roll a sum of $3.$"
Long-Term Proportion of "Rolling a Sum of 3"
| Empirical Probability | |||
| Number of Rolls |
Empirical Definition of Probability
$$P(A)=\frac{\mbox{Observed # of Times Event $A$ Occurs}}{\mbox{Number of Trials}}$$
The Ground Rules of Probability: Any valid probability model must obey the following rules.
Rule #1 The probability of any event $A$ is between $0$ and $1.$ That is, $0 \leq P(A) \leq 1$.
Rule #2 The probability of the sample space is always $1.$ That is $P(S)=1$.
Rule #3 The probability of an event $A$ NOT occurring is $1-P(A)$. That is, $P(A')=1-P(A)$.
The OR Event
Let's roll a fair die. The sample space is $S=\{1,2,3,4,5,6\}.$
What is the probability of rolling an even number OR a perfect square? Let's call this event $X.$
One way to answer this question is to list all numbers between $1$ and $6$ which are even or a perfect square: $1,2,4,6.$
So $X=\{1,2,4,6\}.$
What is $P(X)?$
The OR Event
Another way to think about this situation is to consider the events "roll an even number" and "roll a perfect square" as separate events, call them $A$ and $B.$
Then $A=\{2,4,6\}$, and $B=\{1,4\}.$
Form their union $A \cup B=\{1,2,4,6\}.$
Then the probability of event $A$ or $B$ (roll even or perfect square) is given by
$\displaystyle P(A \cup B)=\frac{2}{3}$
The AND Event
Again, let's roll a fair die. The sample space is still $S=\{1,2,3,4,5,6\}$
What is the probability of rolling an even number AND a perfect square? Let's call this event $Y$.
One way to answer this question is to list all numbers between $1$ and $6$ which are even AND a perfect square: $4.$
So $Y=\{4\}$.
What is $P(Y)?$
The AND Event
Again we consider the events "roll an even number" and "roll a perfect square" as separate events called $A$ and $B$, respectively.
Again $A=\{2,4,6\}$, and $B=\{1,4\}$.
This time we form their intersection $A \cap B=\{4\}$.
Then the probability of event $A$ and $B$ (roll even AND perfect square) is given by
$\displaystyle P(A \cap B)=\frac{1}{6}$
Conditional Probability
Sometimes knowing that one event happened or will happen influences the probability that another will occur.
Example: Roll a fair die. Knowing that the outcome will be even changes the probability of coming up $6.$
The probability goes from $\displaystyle \frac{1}{6}$ to ________ ?
Fact: when you know that the outcome will be even, your sample space is reduced from $\{1,2,3,4,5,6\}$ to $\{2,4,6\}$.
Therefore, the likelihood of rolling a $6$ increases to $\displaystyle \frac{1}{3}.$
Definition: The conditional probability that $A$ will occur given that $B$ has or will occur is denoted as $P(A|B)$ and is given by $$P(A|B)=\frac{P(A \cap B)}{P(B)}.$$
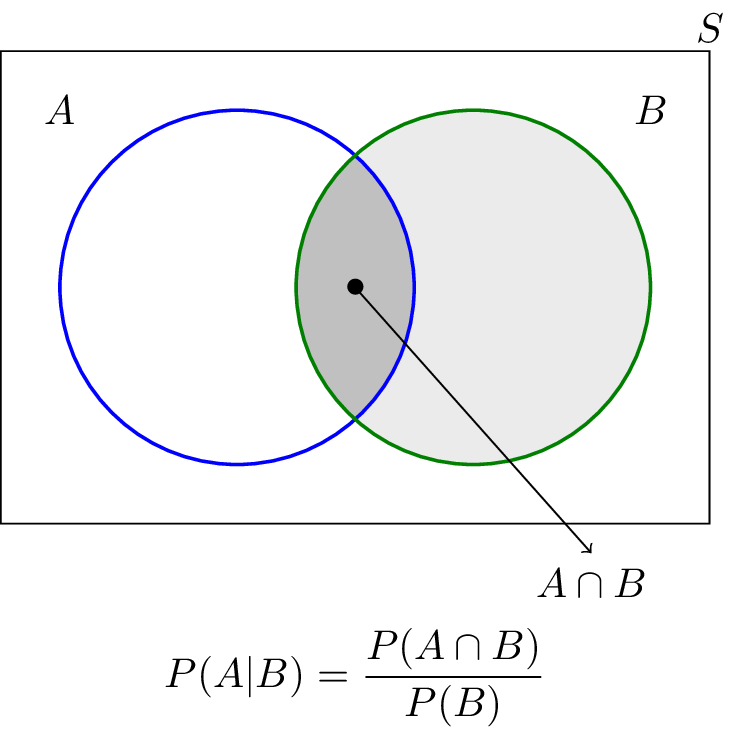
Example
Again we consider the events "roll an even number" and "roll a perfect square" as separate events called $A$ and $B$, respectively.
Again $A=\{2,4,6\}$, and $B=\{1,4\}$.
Find the probabilities $P(A|B)$ and $P(B|A).$
$$
\begin{array}{lll}
\displaystyle P(A|B)&\displaystyle=\frac{P(A \cap B)}{P(B)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{P(\{4\})}{P(\{1,4\})} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1/6}{2/6} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{2} &\mbox{}\\
\end{array}
$$
$$
\begin{array}{lll}
\displaystyle P(B|A)&\displaystyle=\frac{P(B \cap A)}{P(A)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{P(\{4\})}{P(\{2,4,6\})} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1/6}{3/6} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{3} &\mbox{}\\
\end{array}
$$
Example
Suppose an experiment has the outcomes $1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,$ and $12$ where each outcome has an equal chance of occurring.
Let event $A = \{1, 2, 3, 4, 5, 6\}$ and event $B = \{6, 7, 8, 9\}.$
Use the Venn diagram below to compute the probabilities: $P(A')$, $P(B')$, $P(A \cup B)$, $P(A \cap B)$, $P(A|B)$, and $P(B|A)$.
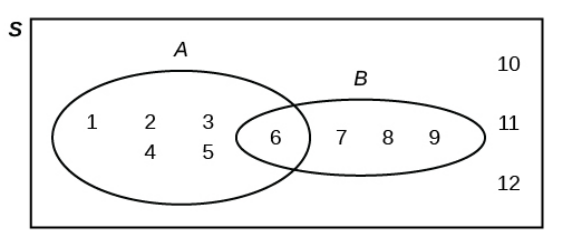
$\displaystyle P(A')=P(\{7,8,9,10,11,12\})=\frac{6}{12}=\frac{1}{2}$
$\displaystyle P(B')=P(\{1,2,3,4,5,10,11,12\})=\frac{8}{12}=\frac{2}{3}$
$\displaystyle P(A \cup B)=P(\{1,2,3,4,5,6,7,8,9\})=\frac{9}{12}=\frac{3}{4}$
$\displaystyle P(A \cap B)=P(\{6\})=\frac{1}{12}$
$\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}=\frac{1/12}{4/12}=\frac{1}{4}$
$\displaystyle P(B|A)=\frac{P(B \cap A)}{P(A)}=\frac{1/12}{6/12}=\frac{1}{6}$
$\displaystyle P(B')=P(\{1,2,3,4,5,10,11,12\})=\frac{8}{12}=\frac{2}{3}$
$\displaystyle P(A \cup B)=P(\{1,2,3,4,5,6,7,8,9\})=\frac{9}{12}=\frac{3}{4}$
$\displaystyle P(A \cap B)=P(\{6\})=\frac{1}{12}$
$\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}=\frac{1/12}{4/12}=\frac{1}{4}$
$\displaystyle P(B|A)=\frac{P(B \cap A)}{P(A)}=\frac{1/12}{6/12}=\frac{1}{6}$