Question: what are some common statistics you hear about on the news, radio, advertisements, etc.?
Averages: an average is a measure of the center of a distribution. We often call this value the mean and write it as $\overline{x}$
Warning: averages are the most abused statistics on earth!
Example: Find the mean of the data set: 3, 3, 4, 5, 7.
In general, to find the mean of a data set $x_1$, $x_2$, $x_3$,...,$x_n$,
we add up all the observations and divide by the total number of observations.
Using fancy mathematical notation, we write $$ \overline{x}=\frac{x_1+x_2+x_3+\cdots+x_n}{n}=\frac{\sum_\limits{j=1}^{n} x_j}{n} $$
Using fancy mathematical notation, we write $$ \overline{x}=\frac{x_1+x_2+x_3+\cdots+x_n}{n}=\frac{\sum_\limits{j=1}^{n} x_j}{n} $$
Another Measure of Center: The Median. The median is literally the middle value of a data set when we line them all up in order.
Example: Find the median of the data set: 3, 3, 4, 5, 7.
Example: Find the median of the data set: 3, 4, 5, 7.
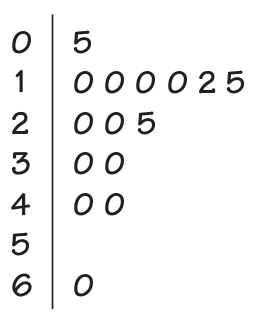
Example: Consider a data set of the travel times in minutes for 15 workers in North Carolina, chosen at random by the Census Bureau which is summarized by the stem plot below.
Here's a nice fun thought experiment: Consider the data set
3, 3, 4, 5, 1000000.
What is the mean of this data set? What is the median?
Example: Suppose the firm "Shady Real-Estate" is advertising a property for sale on Klickatat street which is located in a bad area of town. Strangely, an eccentric billionaire has decided to build a house on this street. The following are the prices of the properties on Klickatat street:
10,000, 20,000, 35,000, 42,000, 60,000, 10,000,000.
What do you think? To entice buyers, Shady Real Estate will report
(a) the mean property value on Klickatat street, or
(b) the median property value on Klickatat street
Savvy Citizen Fact #1: the mean is very sensitive to extreme observations in data.
The median on the other hand, is not sensitive to extreme observations.
This is why we say that the median is a resistant measure of center.
The mean is therefore NOT a resistant measure of center.
Comparing Means and Medians
The mean and median of a roughly symmetric distribution are close together.
In a skewed distribution, the mean is usually farther out in the long tail than is the median.
Measures of Center Aren't Enough. To describe a distributions we need more than its center.
Example. Consider the two data sets below:
Data Set 1:
-1, 0, 1
Data Set 2:
-1000000, 0, 1000000
(a) What are the mean and median of Data Sets 1 and 2?
(b) Do the mean and median alone adequately describe these distributions?
Example: Sleazy P. Martini is a real estate agent for "Shady Real-Estate" and wants to sell you a property for which for which he says "the average yearly temperature is a lovely 60.2 degrees!"
As a statistically savvy citizen, what questions would you ask Mr. Martini?

Quote of the Day
"A person with their feet in the freezer and their head in the oven is on the average quite comfortable."
Savvy Citizen Fact #2: Any useful description of a distribution should will include not only a measure of center, but also a measure of spread.
By spread, we simply mean how much variation there is in a data set.
For example, how spread out is the the data set 5, 5, 5, 5, 5, 5.
How spread out is the the data set 2, 5, 4, 7, 7, 5.
How spread out is the the data set 26, -50, 4, -40, 40, 50
Example. Travel times to work in New York State are (on the average) longer than in North Carolina. Here are the travel times in minutes of 20 randomly chosen New York workers:
10, 30, 5, 25, 40, 20, 10, 15, 30, 20, 15, 20, 85, 15, 65, 15, 60, 60, 40, 45
Arranging these times in ascending order we have
5, 10, 10, 15, 15, 15, 15, 20, 20, 20 | 25, 30, 30, 40, 40, 45, 60, 60, 65, 85
Indicating the medians of the lower 50% and the upper 50% of the data set we have
5, 10, 10, 15, 15 | 15, 15, 20, 20, 20 | 25, 30, 30, 40, 40 | 45, 60, 60, 65, 85
The above gives us a way to describe a distribution with a set of 5 numbers:
5, 15, 22.5, 42.5, 85
The numbers
5, 15, 22.5, 42.5, 85
are a good summary of the New York travel time data as it gives both a measure of the distribution's center and spread.
This collection of numbers actually has a name: the five number summary,
and is in general reported as
Minimum, Quartile 1, Median, Quartile 3, Maximum
Of course, you should always plot your data to get a sense of your distribution too!
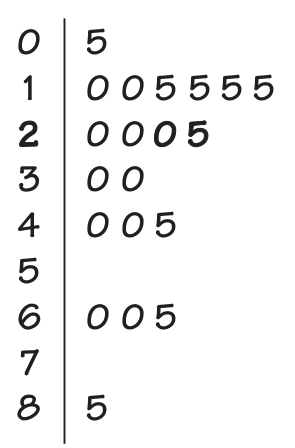
Box Plots graphically display the five number summary.
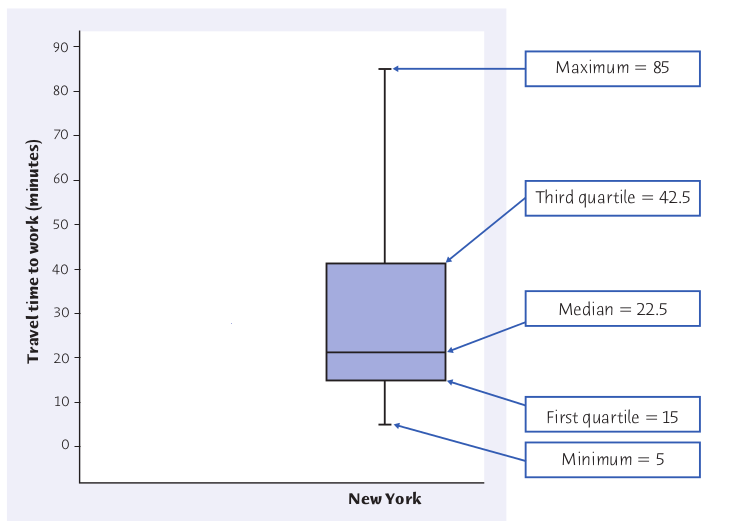
Comparing the box plot of the New York Travel Time data to its stemplot...

Another Measure of Spread: Standard Deviation
The most common measure of spread is not the quartiles, but the standard deviation.
Standard deviation is like an "average deviation" from the mean.
Example. The standard deviation of the data set 2, 2, 2 is 0.
Example. The standard deviation of the data set 1, 2, 3 is 1.
Example. The standard deviation of the data set 0, 2, 4 is 2.
Example: Georgia Southern University had 2417 students with regular admission in their freshman class of 2010. Here are the first five SAT Critical Reading scores from that data set:
650, 490, 580, 450, 570
The mean is $\overline{x}=548$.
$$ \begin{array}{ccc} \hline \mbox{Data Points} & \mbox{Deviations from the mean} & \mbox{Squared Deviations}\\ \hline 650 & 650 - 548 = 102 & 102^2 = 10,404 \\ \hline 490 & 490 - 548 = -58 & (-58)^2 = 3,364 \\ \hline 580 & 580 - 548 = 32 & 32^2 = 1,024 \\ \hline 450 & 450 - 548 = -98 & (-98)^2 = 9,604 \\ \hline 570 & 570 - 548 = 22 & 22^2 =484 \\ \hline & Sum=0 & Sum=24,880\\ \end{array} $$
The variance is $\frac{24,880}{4}=6220$.
The standard deviation is: $\sqrt{6220}\approx 78.87$.
Definition. The variance is the "average" of the squared deviations from the mean, and the standard deviation is the square root of the variance.
In general, to find the standard deviation $s$ of a data set
$x_1$, $x_2$, $x_3$,...,$x_n$, we
1) Compute the mean $\overline{x}$.
2) Compute the deviations from the mean.
These are $\,\,\,\,x_1-\overline{x}$, $\,\,\,\,x_2-\overline{x}$, $\ldots$, $\,\,\,\,x_n-\overline{x}$
3) Square all the deviations from the mean:
$(x_1-\overline{x})^2$, $\,\,\,\,(x_2-\overline{x})^2$, $\ldots$, $\,\,\,\,(x_n-\overline{x})^2$
4) Add up the squared deviations from the mean: $(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots+(x_n-\overline{x})^2$
5) Divide the result by $n-1$ (the resulting number is the variance)
6) Take a square root (the resulting number is the standard deviation)
The above steps are summarized by the formula $$ s=\sqrt{\frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots+(x_n-\overline{x})^2}{n-1}} =\sqrt{\frac{\sum_\limits{j=1}^{n} (x_j-\overline{x})^2}{n-1}} $$
$x_1$, $x_2$, $x_3$,...,$x_n$, we
1) Compute the mean $\overline{x}$.
2) Compute the deviations from the mean.
These are $\,\,\,\,x_1-\overline{x}$, $\,\,\,\,x_2-\overline{x}$, $\ldots$, $\,\,\,\,x_n-\overline{x}$
3) Square all the deviations from the mean:
$(x_1-\overline{x})^2$, $\,\,\,\,(x_2-\overline{x})^2$, $\ldots$, $\,\,\,\,(x_n-\overline{x})^2$
4) Add up the squared deviations from the mean: $(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots+(x_n-\overline{x})^2$
5) Divide the result by $n-1$ (the resulting number is the variance)
6) Take a square root (the resulting number is the standard deviation)
The above steps are summarized by the formula $$ s=\sqrt{\frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots+(x_n-\overline{x})^2}{n-1}} =\sqrt{\frac{\sum_\limits{j=1}^{n} (x_j-\overline{x})^2}{n-1}} $$
Fact: A VERY common summary of a distribution is the mean $\overline{x}$ and standard deviation $s$.
Warning: this is only a good idea if your distribution is symmetric!
For skewed distributions it is generally better to use the five number summary: Min,Q1,M,Q3,Max.