A linear function has the form $f(x)=mx+b$ and when graphed, gives a line.
$m$ is the slope of the line.
$b$ is the $y$-coordinate of the $y$-intercept $(0,b)$.
Recall: Slope is how steep a line is.
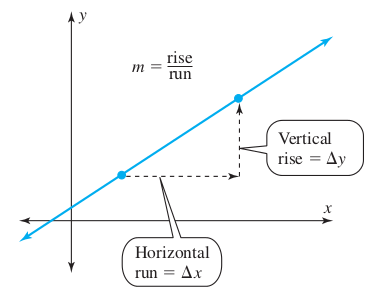
Example: Use the graph to determine the slope of the line.
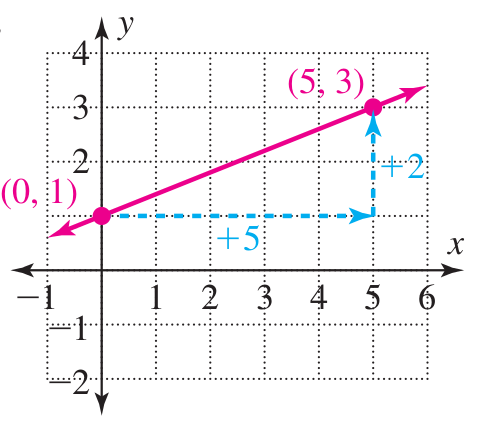
Examples: Find the equation of the linear function pictured below.

Example: Graph the linear function $f(x)=-\frac{2}{3}x+2$.
Formula for Slope: $m=\frac{y_2-y_1}{x_2-x_1}$.

B) Find the equation of the linear function passing through the points $(-6, 2)$ and $(2, 9)$.
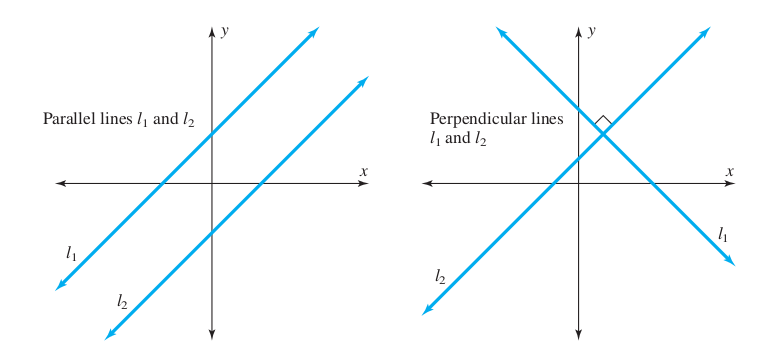
Fact 1: Slopes of parallel lines are equal.
Fact 2: Slopes of perpendicular lines are opposite reciprocals.
Example: Consider the line $L$ passing through the points $(-6, 2)$ and $(2, 9)$.
A) Calculate the slope of a line parallel to $L$.
B) Calculate the slope of a line perpendicular to $L$.

Recall: $x$ and $y$ intercepts.
Fact: The $y$-intercept of a linear function $f(x)=mx+b$ is $(0,b).$ In general, you can always set $x=0.$
Fact: To find the $x$-intercept of a linear function $f(x)=mx+b$, set $f(x)=0$ and solve for $x$.
Example: Find the $x$ and $y$-intercept of the linear function defined by $8x+5y=−6.$
Example: Consider the linear function $f(x)$ graphed below.

B) Determine where $f(x)$ is positive and negative.
Interpretation of Positive/Negative Function Values
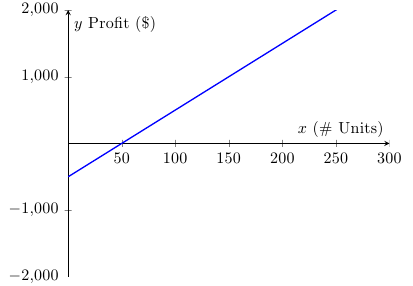
The graph below represents a business's profit $f(x)$ as a function of the number of units $x$ it sells. Assuming this business can meet any demand, use the graph to find the profit and loss intervals for this business.
Interpreting Slope in Applications: The graph gives the distance an automobile has travelled after different periods of time. Determine the slope of this line, and then interpret the meaning of this rate of change.
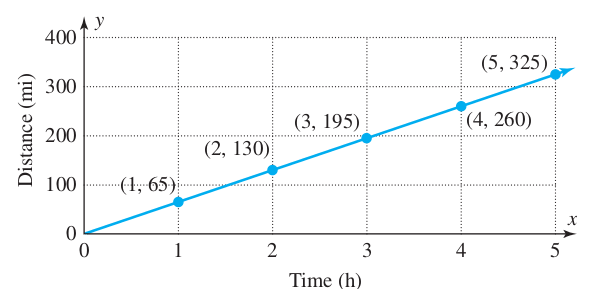
In general, the interpretation of slope is $\frac{\mbox{vertical units}}{\mbox{horizontal units}}$.