Two Related Topics: Exponential Functions and Geometric Sequences.
Fact: "Geometric sequences" are a discrete version of "exponential functions."
Recall "Arithmetic sequences" are a discrete version of "linear functions."
Recall: Arithmetic sequences have a common difference.
Example: The sequence $$a_1=5, \,\,\,\,\, a_2=3, \,\,\,\,\, a_3=1, \,\,\,\,\, a_4=-1, \,\,\,\,\, a_5=-3$$ is arithmetic because there is a common difference of $-2$.
Note: the "common difference" is simply the constant difference between successive values.
Geometric Sequences
Geometric sequences have a common ratio.
Example: The sequence $$a_1=100, \,\,\,\,\, a_2=10, a_3=1, \,\,\,\,\, a_4=0.1, \,\,\,\,\, a_5=0.01$$ is geometric because there is a common ratio of $0.1$.
Note: the "common ratio" is simply the constant ratio between successive values.
Examples
Identify each sequence as "arithmetic," "geometric," or "neither."
$-\frac{2}{3}, \,\, \frac{2}{9}, \,\, -\frac{2}{27}, \,\, \frac{2}{81}, \,\, -\frac{2}{243}$
$7, \,\, 9, \,\, 11, \,\, 13, \,\, 15$
$\frac{28}{9}, \,\, \frac{93}{10}, \,\, \frac{431}{5}, \,\, \frac{74301}{10}, \,\, \frac{552063857}{10}$
Application: Bouncy Ball Physics
A bouncy ball is dropped from 36 m onto a surface which causes it to rebound to $\frac{3}{5}$ of its previous height on each bounce. Determine the heights of the first four bounces: $h_1,$ $h_2,$ $h_3,$ and $h_4.$ Round each height to the nearest hundredth.
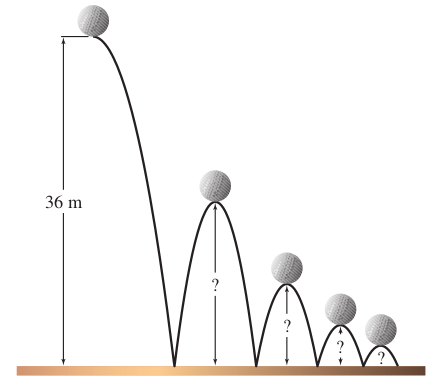
Application: Bouncy Ball Physics

Exponential Functions
Definition: the function $f(x)=b^x$ is called an exponential function.
Note: it will always be the case that $b>0.$
Basic Exponential Functions: Two Examples $$f(x)=3^x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ g(x)=\left(\frac{1}{3}\right)^x$$
Example: Sketch a graph of the function $$f(x)=\left(\frac{1}{2}\right)^x$$ by complete the table of values and plotting points. $$ \begin{array}{c|c} x & f(x) \\ \hline -2 & \\ -1 & \\ 0 & \\ 1 & \\ 2 & \\ \end{array} $$
"Simple" Exponential Equations
Definition: an exponential equation is an equation where the unknown quantity is an exponent.
Example: Solve for $\sigma.$ $$2^{\sigma}=4$$
Process for Solving "Simple" Exponential Equations
1) Massage the equation into the form $b^{\mbox{expression}_1}=b^{\mbox{expression}_2}$.
2) Solve the equation $\mbox{expression}_1=\mbox{expression}_2.$
Example: Solve the exponential equation $2^{9 \phi+3}=\sqrt[4]{2}$
More Examples
$\left(\frac{3}{4}\right)^{5 \sigma+4}=\sqrt{\frac{3}{4}}$
$\left(\frac{1}{2}\right)^{8 b-5}=8$
$\left(\frac{3}{4}\right)^{4 n-9}=1$
A Very Special Base: the number $e$.
The base $e$ is an irrational number which is approximately equal to $2.71.$
This number is a "natural base" for many reasons which will become clearer later.
One of the main reasons: it captures the notion of "continuous growth."
Any exponential function (growth or decay) can be written as $$A(t)=Ae^{rt}$$ where $A$ is an initial quantity and $r$ is the rate of increase or decrease.
Example
The strontium-90 in a nuclear reactor decays continuously. If 40 mg is present initially, the amount present after t years is given by $$A(t)=40e^{-0.0248t}.$$ Approximate to the nearest hundredth of a milligram the amount left after 80 years.