Today we consider graphs of quadratic functions from a different perspective: transformations.
Prototype (Parent) Function: The Squaring Function $$f(x)=x^2$$
Example: Given $f(x)=(x-2)^2,$ complete the table below, sketch a graph of $f(x),$ and determine the domain $D$ and range $R$ of $f(x).$
$
\begin{array}{c|c}
x & f(x) \\ \hline
0 & \\ \hline
1 & \\ \hline
2 & \\ \hline
3 & \\ \hline
\end{array}
$


Graphing Squaring Functions Using Transformations
Example: Graph $f(x)=(x-2)^2+3$
Graphing Quadratic Functions Using Transformations
Step 1: Identify prototype (parent) function: $p(x)=x^2.$
Step 2: Perform shift of $2$ to the right: $y=\,$$\,(x-2)^2.$
Step 3: Perform shift of $3$ upward: $y=$$(x-2)^2$$\,+\,3$
Transformations of $p(x)=x^2$: Vertical and Horizontal Shifts
The graph of $f(x)=\,$$\,(x-h)^2$$\,+\,k$ is the graph of $p(x)=x^2$ shifted to the right by $h$ and up by $k.$
The graph of $f(x)=\,$$\,(x-h)^2$$\,-\,k$ is the graph of $p(x)=x^2$ shifted to the right by $h$ and down by $k.$
The graph of $f(x)=\,$$\,(x+h)^2$$\,+\,k$ is the graph of $p(x)=x^2$ shifted to the left by $h$ and up by $k.$
The graph of $f(x)=\,$$\,(x+h)^2$$\,-\,k$ is the graph of $p(x)=x^2$ shifted to the left by $h$ and down by $k.$
Graphing Quadratic Functions Using Transformations
Example: $g(x)=(x+1)^2-2$

Recap
$f(x)=$ $(x-2)^2$ $+\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ $g(x)=$$(x+1)^2$ $-\,2$
Graphs of Quadratic Functions
Example: Write the formula for the function of each graph below.
Other Transformations: Stretching and Reflecting
Example: Graph $f(x)=-2(x+3)^2+4.$
Step 1: Identify prototype (parent) function: $p(x)=x^2.$
Step 2: Perform shift of $3$ to the left: $y=\,$$\,(x+3)^2.$
Step 3: Perform stretch vertically by $2$: $y=$$\,2\,$$(x+3)^2$
Step 3: Perform reflect over $x$-axis with $-$ sign: $y=$$\,-2\,$$(x+3)^2$
Step 4: Perform shift of $4$ upward: $y=$ $-2$ $(x+3)^2$$\,+\,4$
Transformations of $p(x)=x^2$: Vertical Stretching, Compressing, and Flipping
The graph of $f(x)=\,$$a$$\,x^2$ is the graph of $p(x)=x^2$ vertically stretched or compressed by a factor of $a.$
The graph of $f(x)=\,$$-$$\,x^2$ is the graph of $p(x)=x^2$ reflected over the $x$-axis.
The graph of $f(x)=\,$$-a$$\,x^2$ is
the graph of $p(x)=x^2$ reflected over the $x$-axis and then vertically stretched/compressed by $a.$
Order of Transformations
Generally speaking, when using transformations to graph a function, we work from the inside out.
When performing transformations on $p(x)=x^2:$
Perform horizontal shifts first.
Perform vertical stretching/compressing/flipping second.
Perform vertical shifts third.
Example: Graph $g(x)=0.25(x-1)^2+2$

Recap
$f(x)=\,$$-2$ $(x+3)^2$ $+\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ $g(x)=$$\,0.25\,$$(x-1)^2$ $+\,2$
Domain and Range of Quadratic Functions
Let $f(x)=ax^2+bx+c$ be any quadratic function, and suppose $f(x)=a(x-h)^2+k$ is its vertex form.
The domain of $f(x)$ is $D=(-\infty,\infty).$
The range of $f(x)$ is:
- $R=[k,\infty)$ if $a \gt 0,$ OR
- $R=(-\infty,k]$ if $a \lt 0.$
Example: Find the domain and range of $f(x)=-2x^2-12x-14$
First we find the $x$ coordinate of the vertex point, $h.$
$$
\begin{array}{lll}
\displaystyle h&\displaystyle=-\frac{b}{2a} &\mbox{}\\
\displaystyle &\displaystyle=-\frac{-12}{2(-2)} &\mbox{}\\
\displaystyle &\displaystyle=-3 &\mbox{}\\
\end{array}
$$
We now find the $y$ coordinate of the vertex point, $k.$
$$
\begin{array}{lll}
\displaystyle f(-3)&\displaystyle=-2(-3)^2-12(-3)-14 &\mbox{}\\
\displaystyle &\displaystyle=4 &\mbox{}\\
\end{array}
$$
Since $a=-12 \lt 0,$ the range of $f(x)$ is
$$
R=(-\infty,4]
$$
To confirm our result, here's a graph of $f(x)=-2x^2-12x-14.$
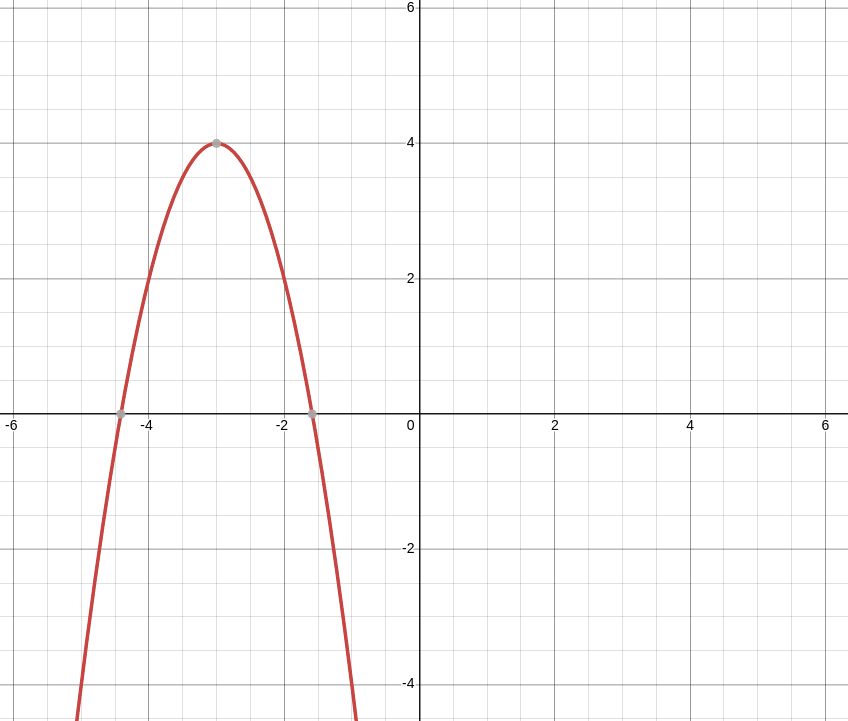
To confirm our result, here's a graph of $f(x)=-2x^2-12x-14.$

Quadratic Function Application: Optimization
A gardener has $640$ feet of fencing to fence in a rectangular garden. One side of the garden is bordered by the Ascii river and so it does not need any fencing.
What dimensions would guarantee that the garden has the greatest possible area?
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
The area of the garden will is given by $$A=\ell w$$
The total length of the fence is twice the length plus the width of the garden $(2\ell + w)$ as seen in the figure above.
Since the gardener has a total of $640$ feet of fencing, we can say $$ 2\ell+w=640 $$ We now combine the two equations above. First, we solve for $\ell$ in the second equation. $$ \begin{array}{lll} &\displaystyle 2\ell+w=640 &\mbox{}\\ \implies &\displaystyle 2\ell=640-w&\mbox{}\\ \implies &\displaystyle \ell=\frac{640-w}{2}&\mbox{}\\ \implies &\displaystyle \ell=320-0.5w&\mbox{}\\ \end{array} $$ We may now plug this into the first equation. $$ \begin{array}{lll} \displaystyle A&\displaystyle=\ell w &\mbox{}\\ \displaystyle &\displaystyle=(320-0.5w)w &\mbox{}\\ \displaystyle &\displaystyle=320w-0.5w^2 &\mbox{}\\ \end{array} $$ Thus, we have a quadratic function which gives us the area in terms of the width. $$ A(w)=-0.5w^2+320w $$ The graph of this function is seen below.
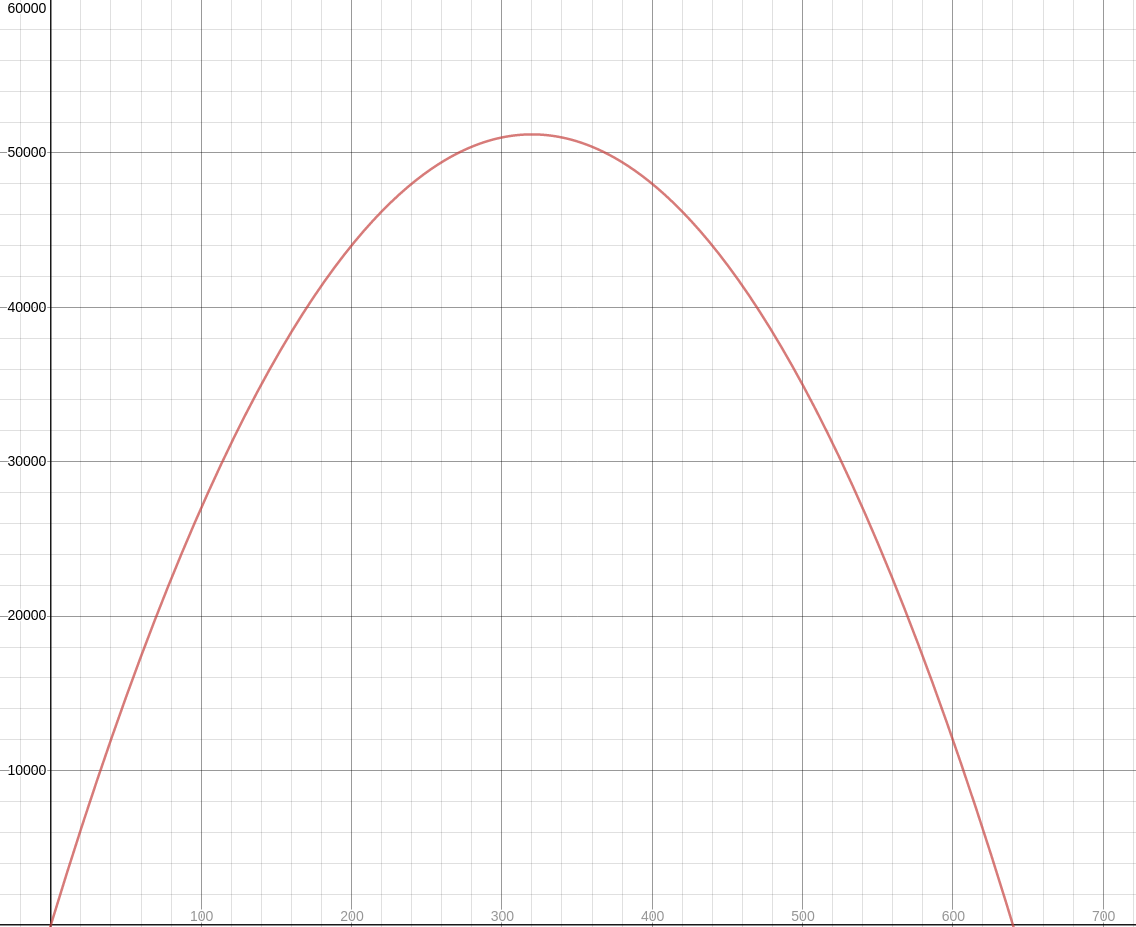
The point on the graph of this function which corresponds to the maximum area is the vertex. (The highest point!)
In this case First we find the $w$ coordinate of the vertex point, $h.$ $$ \begin{array}{lll} \displaystyle h&\displaystyle=-\frac{320}{2(-0.5)} &\mbox{}\\ \displaystyle &\displaystyle=320&\mbox{}\\ \end{array} $$ The width of the maximum area is $320$ feet. And since $$ \ell=320-0.5w=320-0.5\cdot 320=160 $$ the length of maximum area is $160$ feet.
Oh the Possibilities! Choose a width:
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~