A Generic Quadratic Function: $f(x)=ax^2+bx+c$.
Fact: Every quadratic function is the shape of a parabola.
Important Features of a Quadratic Function
1) $y$-intercept
2) $x$-intercept(s) (not every quadratic function has $x$-intercepts)
3) Vertex.
4) Axis of Symmetry
5) Opens Up or Down
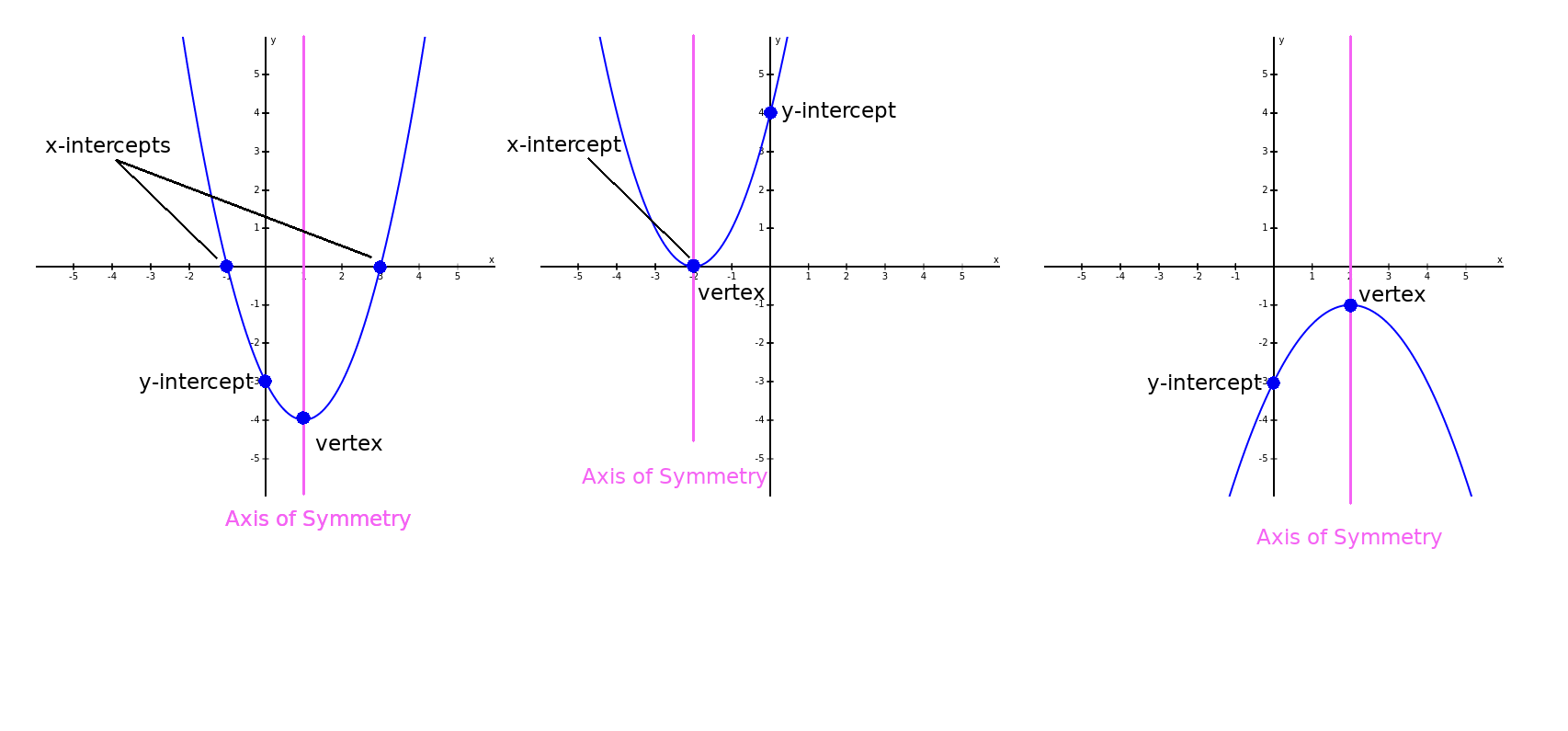
Important Features of a Quadratic Function
For the function $f(x)=ax^2+bx+c$
1) The $y$-intercept is $(0,c).$
2) To find the $x$-intercept(s), solve $ax^2+bx+c=0.$
3) Vertex. The $x$-coordinate is $\displaystyle -\frac{b}{2a}$. The $y$-coordinate is $\displaystyle f\left(-\frac{b}{2a}\right).$
4) Axis of Symmetry. The axis of symmetry has the equation $\displaystyle x=-\frac{b}{2a}$.
5) Opens Up or Down: If $a$ is positive, the parabola opens up. If $a$ is negative, the parabola opens down.
One More Fun-Filled Fact
Every quadratic function $f(x)=ax^2+bx+c$ can be written in the form $$f(x)=a(x-h)^2+k$$ where $(h,k)$ is the vertex point.
Note that $\displaystyle h=-\frac{b}{2a}$ and $\displaystyle k=f\left(-\frac{b}{2a}\right)=f(h).$
Example: For the function $f(x)=2x^{2}-4x-3,$ determine if the parabola opens up or down. Also, find the $x$-intercept points, the $y$-intercept point, and the vertex point. Use this information to graph the function.

Opens Up or Down: Since $a=2 \gt 0,$ the parabola opens upward.
$x$-intercept(s) The $x$-intecept(s) occur where $f(x)=0.$ That is, where $2x^{2}-4x-3=0.$
So, $$ \begin{array}{lll} \displaystyle x&\displaystyle=\frac{-(-4)\pm\sqrt{(-4)^2-4(2)(-3)}}{2(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm\sqrt{40}}{4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm 2\sqrt{10}}{4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{2\pm \sqrt{10}}{2} &\mbox{}\\ \end{array} $$ Thus our $x$-intercept points are $$ \left(\frac{2- \sqrt{10}}{2},0\right)\approx(-0.58,0)\,\,\,\,\mbox{and}\,\,\,\,\left(\frac{2+ \sqrt{10}}{2},0\right)\approx(2.58,0) $$ $y$-intercept The $y$ intercept point is $(0,c)=(0,-3).$
Axis of Symmetry. The axis of symmetry is given by $$ x=-\frac{b}{2a}=-\frac{-4}{2(2)}=1 $$ that is, the line $x=1$ is the axis of symmetry.
Vertex. The vertex occurs where $$ x=-\frac{b}{2a}=-\frac{-4}{2(2)}=1 $$ Thus the vertex point is $$(1,f(1))=(1,2(1)^{2}-4(1)-3)=(1,-5).$$ Below is the sketch of the graph $f(x)=2x^{2}-4x-3$ of using the above calculations.
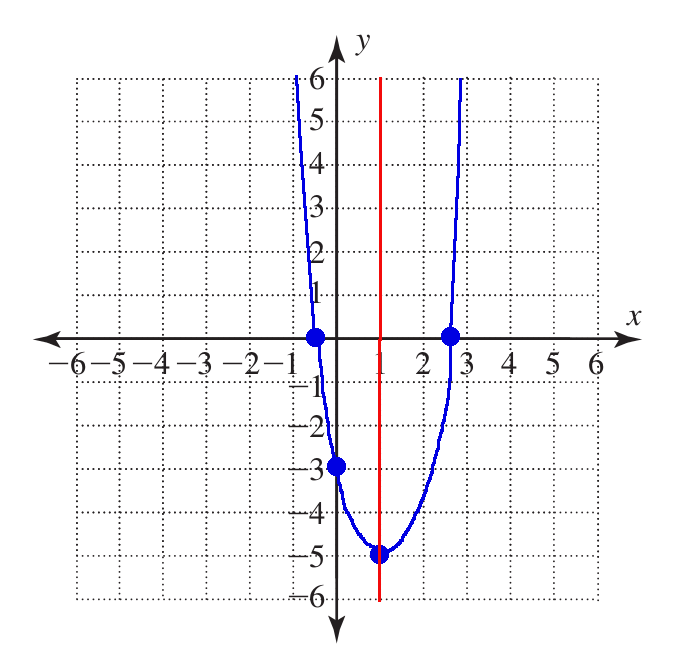
$x$-intercept(s) The $x$-intecept(s) occur where $f(x)=0.$ That is, where $2x^{2}-4x-3=0.$
So, $$ \begin{array}{lll} \displaystyle x&\displaystyle=\frac{-(-4)\pm\sqrt{(-4)^2-4(2)(-3)}}{2(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm\sqrt{40}}{4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm 2\sqrt{10}}{4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{2\pm \sqrt{10}}{2} &\mbox{}\\ \end{array} $$ Thus our $x$-intercept points are $$ \left(\frac{2- \sqrt{10}}{2},0\right)\approx(-0.58,0)\,\,\,\,\mbox{and}\,\,\,\,\left(\frac{2+ \sqrt{10}}{2},0\right)\approx(2.58,0) $$ $y$-intercept The $y$ intercept point is $(0,c)=(0,-3).$
Axis of Symmetry. The axis of symmetry is given by $$ x=-\frac{b}{2a}=-\frac{-4}{2(2)}=1 $$ that is, the line $x=1$ is the axis of symmetry.
Vertex. The vertex occurs where $$ x=-\frac{b}{2a}=-\frac{-4}{2(2)}=1 $$ Thus the vertex point is $$(1,f(1))=(1,2(1)^{2}-4(1)-3)=(1,-5).$$ Below is the sketch of the graph $f(x)=2x^{2}-4x-3$ of using the above calculations.

Example: Find the equation of the quadratic function graphed below and write it in the form $f(x)=ax^2+bx+c.$
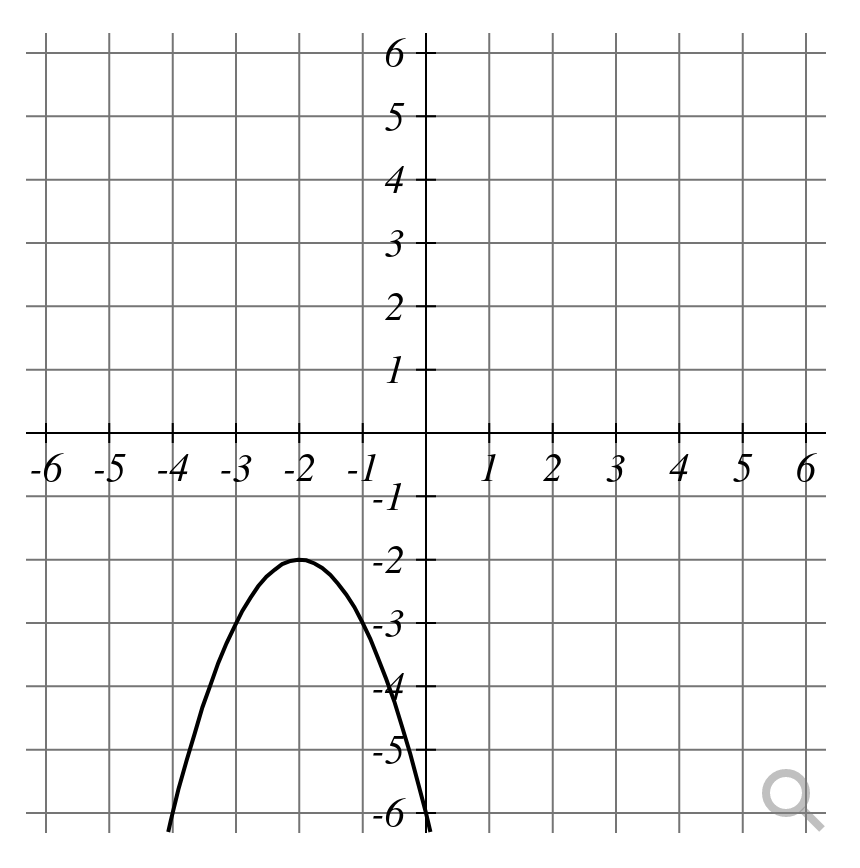
We shall use the form $f(x)=a(x-h)^2+k$ where $(h,k)$ is the vertex point.
From the graph we see that the vertex point is $(h,k)=(-2,-2).$ So, $$ \begin{array}{lll} f(x)&=a(x-(-2))^2+(-2)\\ &=a(x+2)^2-2\\ \end{array} $$ To find $a,$ we may plug in another known point. The $y$-intercept point is $(0,-6).$
Thus $$ -6=f(0)=a(0+2)^2-2 $$ So, $$ \begin{array}{lll} &\displaystyle -6=4a-2&\mbox{}\\ \implies &\displaystyle -4=4a&\mbox{}\\ \implies &\displaystyle a=-1&\mbox{}\\ \end{array} $$ The equation for the parabola is then $$ f(x)=-(x+2)^2-2 $$ Since $$ \begin{array}{ll} -(x+2)^2-2&=-(x^2+4x+4)-2\\ &=-x^2-4x-4-2\\ &=-x^2-4x-6\\ \end{array} $$ we may express $f(x)$ in standard form as $$ f(x)=-x^2-4x-6 $$
From the graph we see that the vertex point is $(h,k)=(-2,-2).$ So, $$ \begin{array}{lll} f(x)&=a(x-(-2))^2+(-2)\\ &=a(x+2)^2-2\\ \end{array} $$ To find $a,$ we may plug in another known point. The $y$-intercept point is $(0,-6).$
Thus $$ -6=f(0)=a(0+2)^2-2 $$ So, $$ \begin{array}{lll} &\displaystyle -6=4a-2&\mbox{}\\ \implies &\displaystyle -4=4a&\mbox{}\\ \implies &\displaystyle a=-1&\mbox{}\\ \end{array} $$ The equation for the parabola is then $$ f(x)=-(x+2)^2-2 $$ Since $$ \begin{array}{ll} -(x+2)^2-2&=-(x^2+4x+4)-2\\ &=-x^2-4x-4-2\\ &=-x^2-4x-6\\ \end{array} $$ we may express $f(x)$ in standard form as $$ f(x)=-x^2-4x-6 $$
The Discriminant of a Quadratic and its Graph

Example: For each of the following graphs, say if the discriminant is positive, negative, or zero.

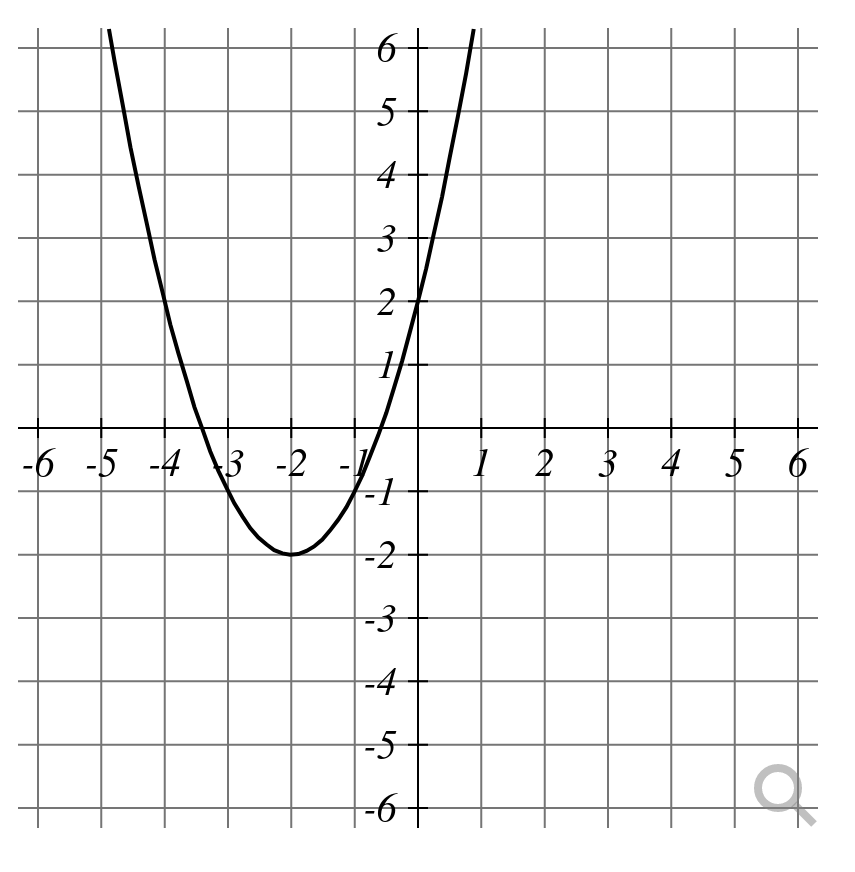
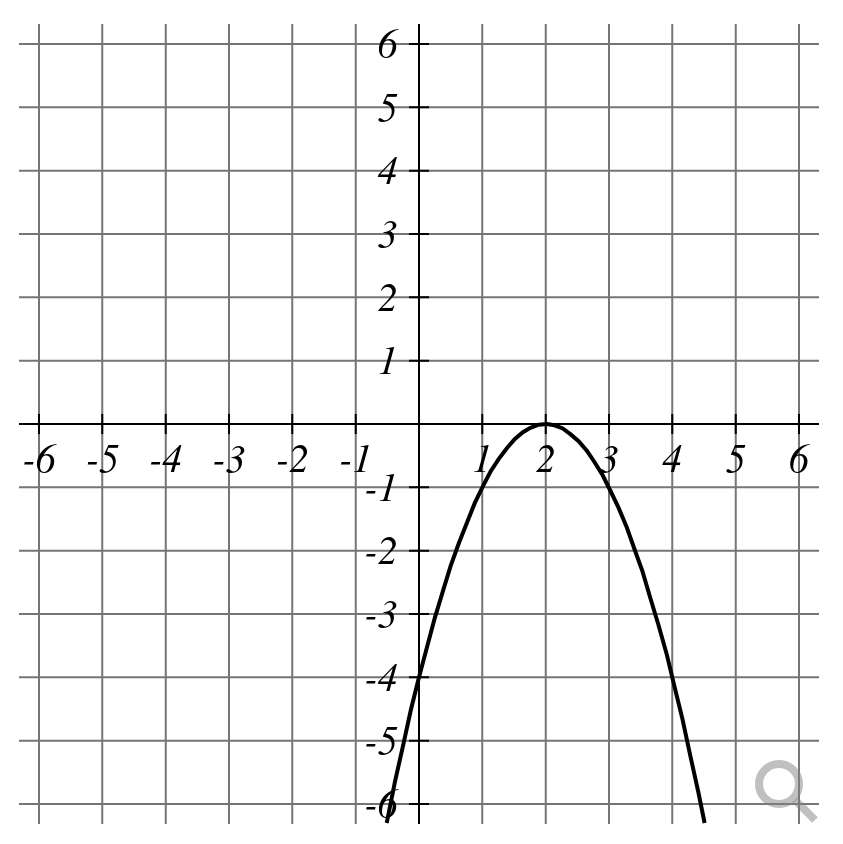
Application: Projectile Motion
Ignoring air resistance, the height $h$ in feet of a potato shot from a potato cannon at the top of a $71$-foot high cliff can be modelled by the function $h(t)= -16t^2 + 106t + 71,$ where $t$ represents the time in seconds since the cannon was fired.
(a) When will the potato reach its maximum height?
(b) At this point in time, what will be the potato's maximum height?
(a) The potato will reach its maximum height at the point corresponding to the vertex on the graph. That is, at
$$
\begin{array}{lll}
\displaystyle t&\displaystyle=-\frac{b}{2a} &\mbox{}\\
\displaystyle &\displaystyle=-\frac{106}{2(-16)} &\mbox{}\\
\displaystyle &\displaystyle=3.3125&\mbox{}\\
\end{array}
$$
The potato will reach its maximum height at $t=3.3125$ seconds.
(b) The maximum height of the potato can be found by evaluating $h(t)= -16t^2 + 106t + 71$ at $t=3.3125$ seconds. $$ \begin{array}{lll} \displaystyle h(3.3125)&\displaystyle=-16(3.3125)^2 + 106(3.3125) + 71 &\mbox{}\\ \displaystyle &\displaystyle=246.5625 &\mbox{}\\ \end{array} $$ The maximum height of the potato is $246.5625$ feet.
A graph of $h(t)= -16t^2 + 106t + 71$ confirms the above calculations.
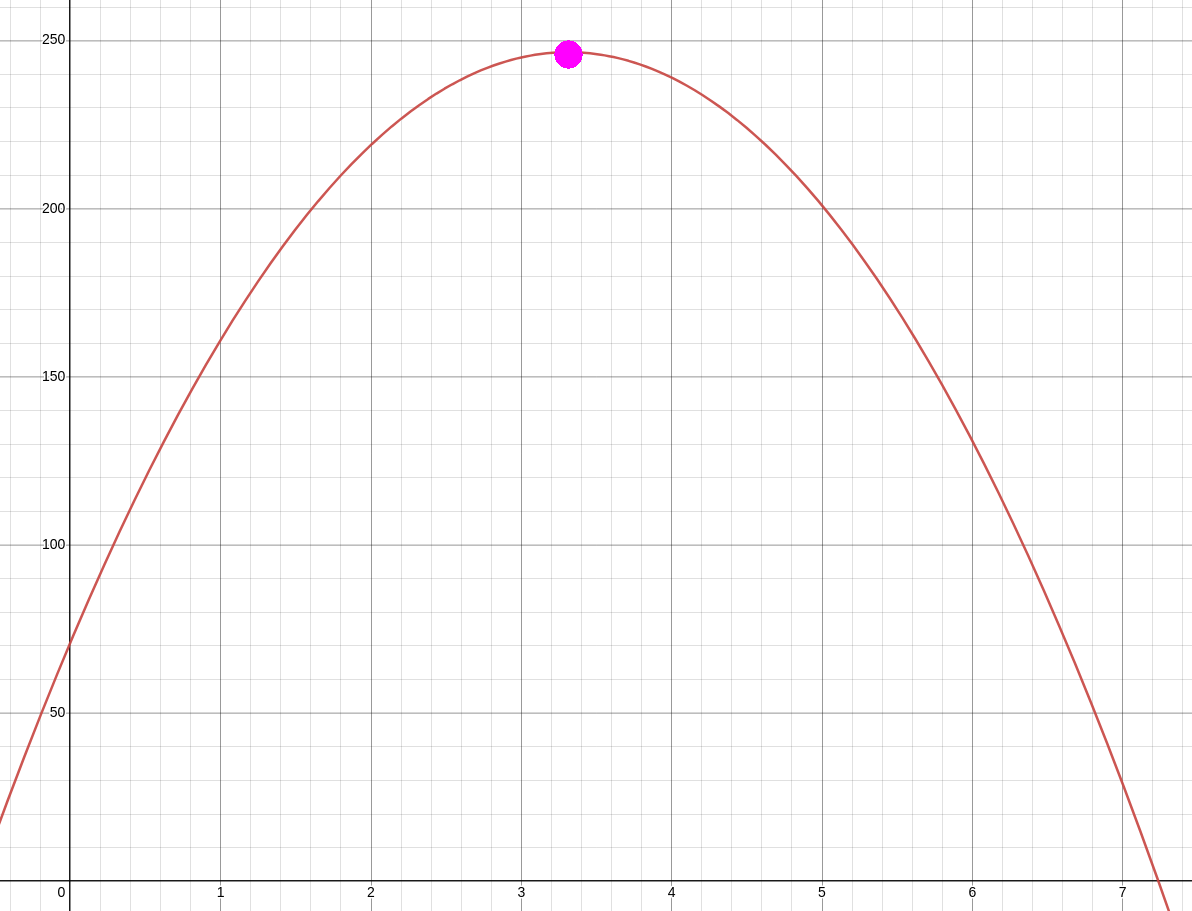
(b) The maximum height of the potato can be found by evaluating $h(t)= -16t^2 + 106t + 71$ at $t=3.3125$ seconds. $$ \begin{array}{lll} \displaystyle h(3.3125)&\displaystyle=-16(3.3125)^2 + 106(3.3125) + 71 &\mbox{}\\ \displaystyle &\displaystyle=246.5625 &\mbox{}\\ \end{array} $$ The maximum height of the potato is $246.5625$ feet.
A graph of $h(t)= -16t^2 + 106t + 71$ confirms the above calculations.

Quadratic Function Application: Optimization
A gardener has $640$ feet of fencing to fence in a rectangular garden. One side of the garden is bordered by the Ascii river and so it does not need any fencing.
What dimensions would guarantee that the garden has the greatest possible area?
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
The area of the garden will is given by $$A=\ell w$$
The total length of the fence is twice the length plus the width of the garden $(2\ell + w)$ as seen in the figure above.
Since the gardener has a total of $640$ feet of fencing, we can say $$ 2\ell+w=640 $$ We now combine the two equations above. First, we solve for $\ell$ in the second equation. $$ \begin{array}{lll} &\displaystyle 2\ell+w=640 &\mbox{}\\ \implies &\displaystyle 2\ell=640-w&\mbox{}\\ \implies &\displaystyle \ell=\frac{640-w}{2}&\mbox{}\\ \implies &\displaystyle \ell=320-0.5w&\mbox{}\\ \end{array} $$ We may now plug this into the first equation. $$ \begin{array}{lll} \displaystyle A&\displaystyle=\ell w &\mbox{}\\ \displaystyle &\displaystyle=(320-0.5w)w &\mbox{}\\ \displaystyle &\displaystyle=320w-0.5w^2 &\mbox{}\\ \end{array} $$ Thus, we have a quadratic function which gives us the area in terms of the width. $$ A(w)=-0.5w^2+320w $$ The graph of this function is seen below.

The point on the graph of this function which corresponds to the maximum area is the vertex. (The highest point!)
In this case First we find the $w$ coordinate of the vertex point, $h.$ $$ \begin{array}{lll} \displaystyle h&\displaystyle=-\frac{320}{2(-0.5)} &\mbox{}\\ \displaystyle &\displaystyle=320&\mbox{}\\ \end{array} $$ The width of the maximum area is $320$ feet. And since $$ \ell=320-0.5w=320-0.5\cdot 320=160 $$ the length of maximum area is $160$ feet.
Oh the Possibilities! Choose a width:
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~
Bonus Application: Economics (Diminishing Returns)
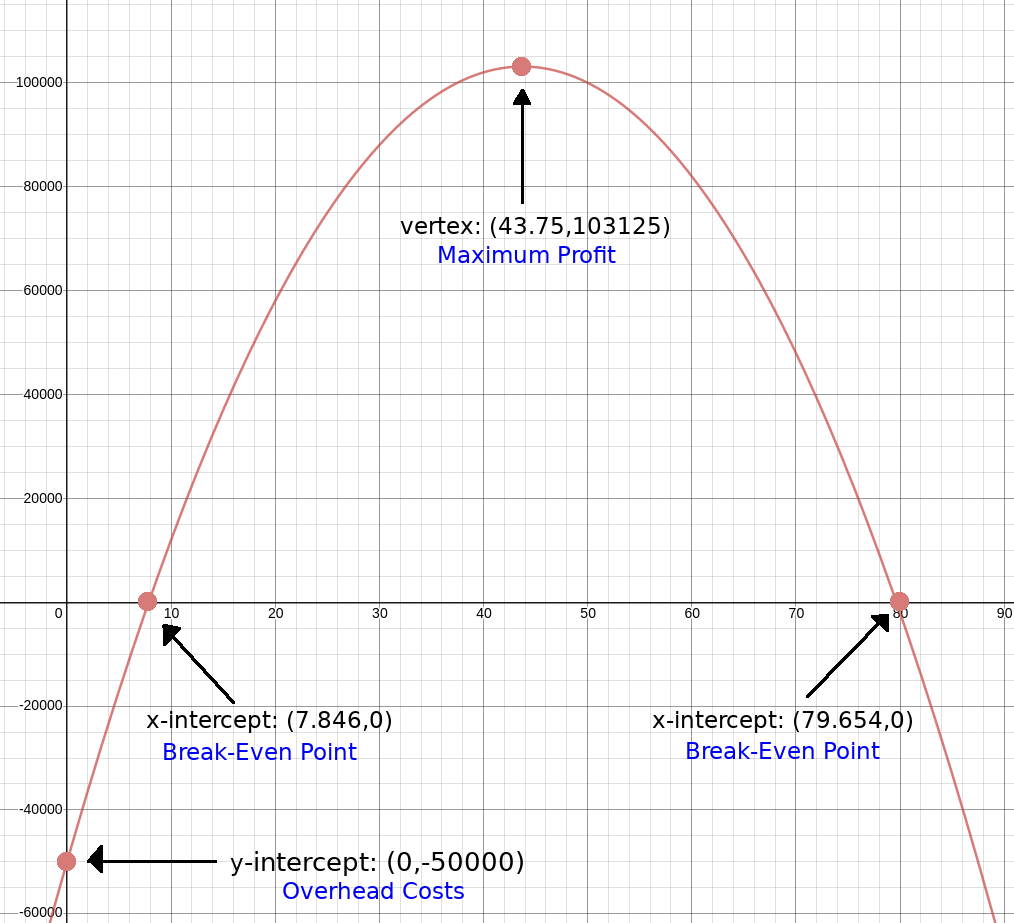
Billy Bob owns a coal mine. One day he noticed, contrary to his expectations, that selling more coal doesn't necessarily mean more profit. Looking at data from the last year, Billy Bob created a function $y=P(x)=-80x^2+7000x-50000$ which gives the profit in dollars when $x$ tons of coal are produced and sold. Help Billy Bob determine the following, and make a graph for Billy Bob using the information you gain from parts a through c:
a. his overhead costs (Hint: Evaluate $P(0).$)
$$P(0)=-80 \cdot 0^2+7000\cdot 0-50000=-50000$$
Billy Bob's overhead costs are $\$\mbox{50,000}.$ That is, before producing any coal, Billy Bob must invest $\$\mbox{50,000}$ in equipment, labor, etc.
Note that $(0,P(0))=(0,-50000)$ is the $y$-intercept of the graph of $y=P(x).$
Note that $(0,P(0))=(0,-50000)$ is the $y$-intercept of the graph of $y=P(x).$
b. the break-even values (Hint: When does $P(x)=0?$) Round your answers to the nearest hundredth.
The break even values occur where $P(x)=0.$ (Billy makes his money back, but with no profit.) Then $$-80x^2+7000x-50000=0$$ $$x=\frac{-7000 \pm \sqrt{7000^2-4(-80)(-50000)}}{2(-80)}$$ $$x=\frac{-7000 \pm \sqrt{33000000}}{-160}$$ $$x=\frac{-7000 \pm 1000\sqrt{33}}{-160}$$ $$x=\frac{-175 \pm 25\sqrt{33}}{-4}$$ $$x=\frac{-175 + 25\sqrt{33}}{-4} \,\,\,\mbox{ OR } \,\,\,\, x=\frac{-175 - 25\sqrt{33}}{-4}$$ $$x\approx 7.846 \,\,\,\mbox{ OR } \,\,\,\, x \approx 79.654$$ That is, Billy Bob breaks even when he produces and sells either $7.846$ or $79.654$ tons of coal.
Note that $(\frac{-175 + 25\sqrt{33}}{-4},0) \approx (7.846,0)$ and $(\frac{-175 - 25\sqrt{33}}{-4},0) \approx (79.654,0)$ are the $x$-intercepts of the graph of $y=P(x).$
c. his maximum profit that can be made and the number of tons to sell to create this profit (find the vertex).
The production amount that gives the maximum profit can be found by locating the vertex point.
The $x$ coordinate of the vertex point (the optimal production amount) is
$$x_{max}=h=\frac{-7000}{2(-80)}=43.75.$$
The maximum profit generated from producing and selling $43.75$ tons of coal is
$$y_{max}=P_{max}=P(43.75)=-80 \cdot 43.75^2+7000\cdot 43.75-50000=103125.$$
In summary, Billy Bob's maximum profit is $\$\mbox{103,125}.$ The amount of coal Billy Bob must produce and sell
to achieve this maximum profit is $43.75$ tons.
Graph of Profit Versus Production