Fact: Applied problems in an algebra class are more often silly than useful.
However...
Such problems are the building blocks of more complex and realistic models of our world.
To learn any skill requires learning rudiments which can assembled into something useful or beautiful.
For example...
An Analogy
A great football player must do many things to achieve greatness on the field.
One of these is strength training.
Will lifting weights alone make a football player great? Is getting strong the the ultimate goal?
Is being strong a basic requirement for being a great football player?
More Analogies
A classical pianist must first learn to read music, practice scales, and train the ear.
Learning a new language requires learning new symbols, vocabulary, and grammar.
To learn how to draw, one must learn perspective, anatomies of living things, and understand the nature of light.
None of the blue items above constitute the practice of their respective disciplines, yet these disciplines cannot be practiced without these skills.
An Analogy
In the same way, to get good at applying mathematical ideas as models of the real world, we must must begin with idealizations and simple situations.
Most of application problems we do in this class will resemble the grunt work of getting good at a worthwhile skill: lifting weights, practicing scales, and learning grammar.
However, there will be some situations when we catch a glimpse of how we may begin applying these ideas in a more realistic way.

Rough Guide for Solving Word Problems
- Step 1: Read. Read the problem carefully to determine what you are being asked to find.
- Step 2: Name Names. Select a variable to represent each unknown quantity. Specify precisely what each variable represents and note any restrictions on each variable.
- Step 3: Translate. If necessary, make a sketch and translate the problem into a word equation or a system of word equations. Then translate each word equation into an algebraic equation.
- Step 4: Solve. Solve the equation, and answer the question completely in the form of a sentence.
- Step 5: Check. Check the reasonableness of your answer.
Problems We'll be Solving: The following kinds of problems often lead to solving quadratic equations.
- Number Problems
- Area Problems
- Problems involving Right-Triangle Geometry (Pythagorean Theorem)
- Projectile Motion
Number Problems
Number problems are truly nerdy and at this level are not super useful.
The basic skill these problems develop is translating verbal statements into mathematical statements.
Example: A Typical Algebra-Level Number Problem
The product of two consecutive odd integers is $255.$
Letting $x$ is the smallest of the integers,
(a) write an equation in terms of $x$ that describes the situation, and
(b) find all such pairs of integers.
Step 1: Read. We have read and understand what the problem is asking for.
Step 2: Name Names. Let $x$ be the first odd integer.
Since $x+1$ is even, $x+2$ is the next odd integer.
Thus, $x(x+2)$ is the product of two consecutive odd integers.
Step 3: Translate. The problem tells us that, "the product of two consecutive odd integers is $255.$"
From the above we have $$ \underbrace{\mbox{The product of two consecutive odd integers}}_{x(x+2)} \underbrace{\mbox{is}}_{=} \underbrace{255.}_{255} $$ So our equation is $$ x(x+2)=255 $$ Step 4: Solve. $$ \begin{array}{lll} &\displaystyle x(x+2)=255 &\mbox{}\\ \implies &\displaystyle x^2+2x=255&\mbox{}\\ \implies &\displaystyle x^2+2x-255=0&\mbox{}\\ \implies &\displaystyle x^2+2x-255=0&\mbox{}\\ \implies &\displaystyle (x-15)(x+17)=0&\mbox{}\\ \implies &\displaystyle x-15=0 \,\,\,\,\mbox{or}\,\,\,\,x+17=0&\mbox{}\\ \implies &\displaystyle x=15 \,\,\,\,\mbox{or}\,\,\,\,x=-17&\mbox{}\\ \end{array} $$ Thus, we have two pairs of consecutive odd integers.
$x=15,$ and $x+2=17$
$x=-17,$ and $x+2=-15$
These are the two pairs of consecutive odd integers.
Step 5: Check. Since $$ 15\cdot 17=255\,\,\,\,\mbox{ and }\,\,\,\,-17\cdot (-15)=255 $$ we have found the pairs of consecutive integers whose product is $15.$
Step 2: Name Names. Let $x$ be the first odd integer.
Since $x+1$ is even, $x+2$ is the next odd integer.
Thus, $x(x+2)$ is the product of two consecutive odd integers.
Step 3: Translate. The problem tells us that, "the product of two consecutive odd integers is $255.$"
From the above we have $$ \underbrace{\mbox{The product of two consecutive odd integers}}_{x(x+2)} \underbrace{\mbox{is}}_{=} \underbrace{255.}_{255} $$ So our equation is $$ x(x+2)=255 $$ Step 4: Solve. $$ \begin{array}{lll} &\displaystyle x(x+2)=255 &\mbox{}\\ \implies &\displaystyle x^2+2x=255&\mbox{}\\ \implies &\displaystyle x^2+2x-255=0&\mbox{}\\ \implies &\displaystyle x^2+2x-255=0&\mbox{}\\ \implies &\displaystyle (x-15)(x+17)=0&\mbox{}\\ \implies &\displaystyle x-15=0 \,\,\,\,\mbox{or}\,\,\,\,x+17=0&\mbox{}\\ \implies &\displaystyle x=15 \,\,\,\,\mbox{or}\,\,\,\,x=-17&\mbox{}\\ \end{array} $$ Thus, we have two pairs of consecutive odd integers.
$x=15,$ and $x+2=17$
$x=-17,$ and $x+2=-15$
These are the two pairs of consecutive odd integers.
Step 5: Check. Since $$ 15\cdot 17=255\,\,\,\,\mbox{ and }\,\,\,\,-17\cdot (-15)=255 $$ we have found the pairs of consecutive integers whose product is $15.$
Example: A Data-Security Number Problem
Find two large prime numbers $p$ and $q$ which do not divide a number $a.$ (The number $a$ represents an encrypted message.)
Then find two numbers $e$ and $d$ such that the remainder is $1$ when dividing their product by $(p-1)(q-1).$
While this is also a nerdy number problem, you have its solution to thank for helping keeping your online communications secure.
Area Problems
Are area problems nerdy? Yes.
But again, such problems help to reinforce the skill of translating a situation into mathematical language.
Moreover, in higher-level courses, areas can be interpreted as much more than the amount of two-dimensional space; areas can represent distances travelled, masses, probabilities, and energies, just to name a few.
Thus, getting comfortable with geometric notions pays huge dividends if you travel further down the road to more advanced mathematics.
Since area problems involve the product of two numbers (often unknown), they lead to quadratic equations.
Example: Area
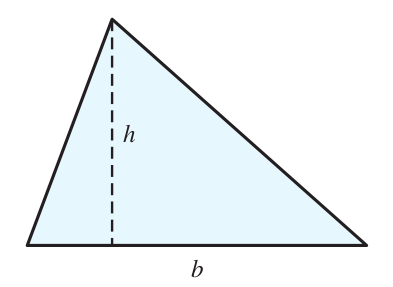
The base of a triangle (see the figure) is $1$ meter longer than the height. Find the base and the height if the area of this triangle is $65$ square meters. If necessary, round your answer to the nearest tenth.
Step 1: Read. We have read and understand what the problem is asking for.
Step 2: Name Names. Let $b$ be the base and $h$ be the height of the triangle.
Step 3: Translate.
We translate the two statements the problem has given us. $$ \underbrace{\mbox{The base of a triangle}}_{b} \underbrace{\mbox{is}}_{=} \underbrace{\mbox{1 meter longer than the height.}}_{h+1} $$ $$ \underbrace{\mbox{The area of a triangle}}_{\frac{1}{2}bh} \underbrace{\mbox{is}}_{=} \underbrace{\mbox{65 square meters.}}_{65} $$ Since $\displaystyle \frac{1}{2}bh=65,$ and since $b=h+1,$ we have $$ \frac{1}{2}(h+1)h=65 $$ Solving this equation will give us the height.
Step 4: Solve.
$$ \begin{array}{lll} &\displaystyle \frac{1}{2}(h+1)h=65&\mbox{}\\ \implies &\displaystyle (h+1)h= 130& \mbox{}\\ \implies &\displaystyle h^2+h=130& \mbox{}\\ \implies &\displaystyle h^2+h-130=0& \mbox{}\\ \implies &\displaystyle h^2+h-130=0& \mbox{}\\ \end{array} $$ Using quadratic formula, we then have $$ \begin{array}{lll} \displaystyle h&\displaystyle=\frac{-(1)\pm\sqrt{(1)^2-4(1)(-130)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-1\pm\sqrt{521}}{2} &\mbox{}\\ \end{array} $$ That is, $$ h=\frac{-1+\sqrt{521}}{2}\approx 10.91271221\,\,\,\,\mbox{or}\,\,\,\,h=\frac{-1-\sqrt{521}}{2}\approx -11.91271221 $$ Since a length cannot be negative, we choose $h \approx 10.91271221.$
So, the height of the triangle is about $10.9$ meters, and the base is about $11.9$ meters.
Step 5: Check. If $b \approx 11.9$ meters and $h\approx 10.9$ meters, then the triangle will have an approximate area of about $$ A=\frac{1}{2}bh\approx \frac{1}{2}(11.9)(10.9)=64.855 $$ Since this is close, our answer is reasonable.
Step 2: Name Names. Let $b$ be the base and $h$ be the height of the triangle.
Step 3: Translate.
We translate the two statements the problem has given us. $$ \underbrace{\mbox{The base of a triangle}}_{b} \underbrace{\mbox{is}}_{=} \underbrace{\mbox{1 meter longer than the height.}}_{h+1} $$ $$ \underbrace{\mbox{The area of a triangle}}_{\frac{1}{2}bh} \underbrace{\mbox{is}}_{=} \underbrace{\mbox{65 square meters.}}_{65} $$ Since $\displaystyle \frac{1}{2}bh=65,$ and since $b=h+1,$ we have $$ \frac{1}{2}(h+1)h=65 $$ Solving this equation will give us the height.
Step 4: Solve.
$$ \begin{array}{lll} &\displaystyle \frac{1}{2}(h+1)h=65&\mbox{}\\ \implies &\displaystyle (h+1)h= 130& \mbox{}\\ \implies &\displaystyle h^2+h=130& \mbox{}\\ \implies &\displaystyle h^2+h-130=0& \mbox{}\\ \implies &\displaystyle h^2+h-130=0& \mbox{}\\ \end{array} $$ Using quadratic formula, we then have $$ \begin{array}{lll} \displaystyle h&\displaystyle=\frac{-(1)\pm\sqrt{(1)^2-4(1)(-130)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-1\pm\sqrt{521}}{2} &\mbox{}\\ \end{array} $$ That is, $$ h=\frac{-1+\sqrt{521}}{2}\approx 10.91271221\,\,\,\,\mbox{or}\,\,\,\,h=\frac{-1-\sqrt{521}}{2}\approx -11.91271221 $$ Since a length cannot be negative, we choose $h \approx 10.91271221.$
So, the height of the triangle is about $10.9$ meters, and the base is about $11.9$ meters.
Step 5: Check. If $b \approx 11.9$ meters and $h\approx 10.9$ meters, then the triangle will have an approximate area of about $$ A=\frac{1}{2}bh\approx \frac{1}{2}(11.9)(10.9)=64.855 $$ Since this is close, our answer is reasonable.
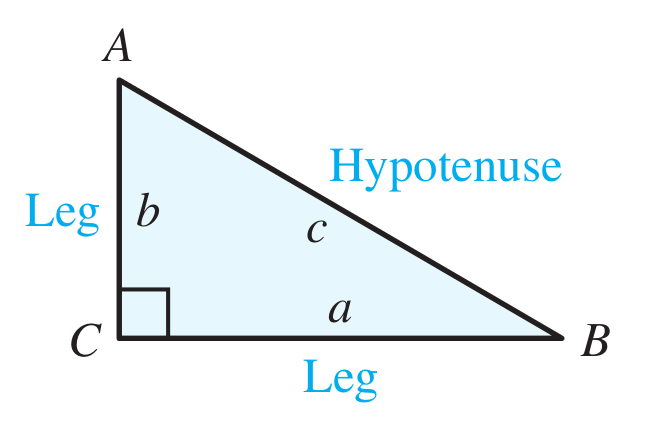
Pythagorean Theorem: Many problems in applied mathematics involve right triangles. In fact, modelling trajectories of projectiles requires an understanding of right-triangle geometry. Thus, a knowledge of the Pythagorean theorem is essential to solving these problems.
For any right triangle, the square of the hypotenuse is the sum of the squares of the legs.
Example: Pythagorean Theorem
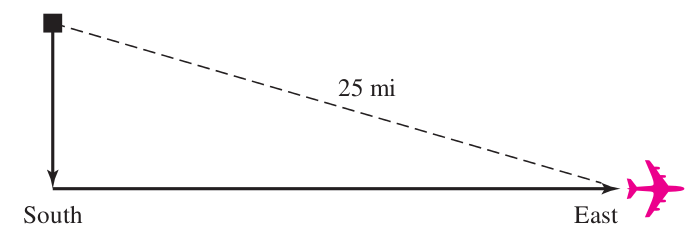
Upon leaving an airport, an airplane flew due south and then due east. After it had flown $14$ miles farther east than it had flown south, it was $25$ miles from the airport. How far south had it flown? Round your answer to two decimal places.
Step 1: Read. We have read and understand what the problem is asking for.
Step 2: Name Names. Let $x$ be the distance the plane flew south.
Step 3: Translate. $$ \underbrace{\mbox{[The plane flew] $14$ miles farther east than it had flown south.}}_{x+14} $$ Translating the above to the figure we have
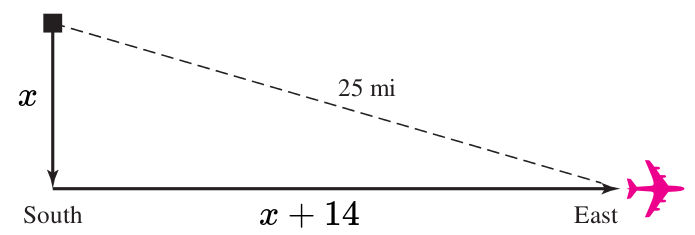
From the figure, and using Pythagorean Theorem, we have $$ x^2+(x+14)^2=25^2 $$ Step 4: Solve. $$ \begin{array}{lll} &\displaystyle x^2+(x+14)^2=25^2&\mbox{}\\ \implies &\displaystyle x^2+x^2+28x+196=625&\mbox{}\\ \implies &\displaystyle 2x^2+28x+196=625&\mbox{}\\ \implies &\displaystyle 2x^2+28x-429=0&\mbox{}\\ \implies &\displaystyle x=\frac{-(28)\pm\sqrt{(28)^2-4(2)(-429)}}{2(2)}&\mbox{}\\ \end{array} $$ Using quadratic formula, we then have $$ \begin{array}{lll} \displaystyle &\displaystyle=\frac{-(28)\pm\sqrt{(28)^2-4(2)(-429)}}{2(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-28\pm\sqrt{4216}}{4} &\mbox{}\\ \end{array} $$ That is, $$ x=\frac{-28+\sqrt{4216}}{4}\approx 9.232683081 \,\,\,\,\mbox{or}\,\,\,\,x=\frac{-28-\sqrt{4216}}{4}\approx -23.23268308 $$ Since a distance cannot be negative, we choose $x \approx 9.232683081.$
Thus, the plane flew about $9.23$ miles south, and then $23.23$ miles east.
Step 5: Check. If $x \approx 9.25$ miles, then the figure we get should be
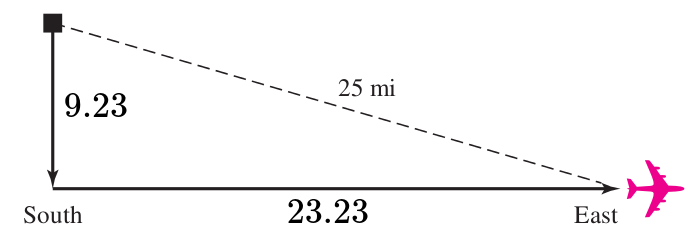 That is, it should be that $9.23^2+23.23^2\approx 25^2,$ and indeed,
$$
\begin{array}{lll}
\displaystyle 9.23^2+23.23^2&\displaystyle=624.8258 &\mbox{}\\
\displaystyle &\displaystyle\approx 625&\mbox{}\\
\displaystyle &\displaystyle=25^2&\mbox{}\\
\end{array}
$$
Our answer is reasonable.
That is, it should be that $9.23^2+23.23^2\approx 25^2,$ and indeed,
$$
\begin{array}{lll}
\displaystyle 9.23^2+23.23^2&\displaystyle=624.8258 &\mbox{}\\
\displaystyle &\displaystyle\approx 625&\mbox{}\\
\displaystyle &\displaystyle=25^2&\mbox{}\\
\end{array}
$$
Our answer is reasonable.
Step 2: Name Names. Let $x$ be the distance the plane flew south.
Step 3: Translate. $$ \underbrace{\mbox{[The plane flew] $14$ miles farther east than it had flown south.}}_{x+14} $$ Translating the above to the figure we have

From the figure, and using Pythagorean Theorem, we have $$ x^2+(x+14)^2=25^2 $$ Step 4: Solve. $$ \begin{array}{lll} &\displaystyle x^2+(x+14)^2=25^2&\mbox{}\\ \implies &\displaystyle x^2+x^2+28x+196=625&\mbox{}\\ \implies &\displaystyle 2x^2+28x+196=625&\mbox{}\\ \implies &\displaystyle 2x^2+28x-429=0&\mbox{}\\ \implies &\displaystyle x=\frac{-(28)\pm\sqrt{(28)^2-4(2)(-429)}}{2(2)}&\mbox{}\\ \end{array} $$ Using quadratic formula, we then have $$ \begin{array}{lll} \displaystyle &\displaystyle=\frac{-(28)\pm\sqrt{(28)^2-4(2)(-429)}}{2(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-28\pm\sqrt{4216}}{4} &\mbox{}\\ \end{array} $$ That is, $$ x=\frac{-28+\sqrt{4216}}{4}\approx 9.232683081 \,\,\,\,\mbox{or}\,\,\,\,x=\frac{-28-\sqrt{4216}}{4}\approx -23.23268308 $$ Since a distance cannot be negative, we choose $x \approx 9.232683081.$
Thus, the plane flew about $9.23$ miles south, and then $23.23$ miles east.
Step 5: Check. If $x \approx 9.25$ miles, then the figure we get should be

Projectile Motion
Fact: When you throw an object in the air, it follows a parabolic path.
In fact, if the object's initial upward velocity is $v_0$, and its initial height is $h_0$, then the equation which describes the height of its trajectory is $$h(t)=-4.9t^2+v_0 t+ h_0$$ if time $t$ is measured in seconds and the height $h$ is measured in meters or $$h(t)=-16t^2+v_0 t+ h_0$$ if time $t$ is measured in seconds and the height $h$ is measured in feet.
The above equations are very good at modelling heights of trajectories at low velocity.

Example: Projectile Motion
Ignoring air resistance, the height $h$ in feet of a potato shot from a potato cannon at the top of a $71$-foot high cliff can be modelled by the function $h(t)= -16t^2 + 106t + 71 $, where $t$ represents the time in seconds since the cannon was fired.
(a) How long will it take for the potato to hit the ground? Round your answers to two decimal places.
(b) Find the two points in time when the potato is $114$ feet above the ground. Round your answers to two decimal places.
(a) The potato will hit the ground when $h(t)=0,$ that is, when $-16t^2 + 106t + 71=0$
We then have $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-(106)\pm\sqrt{(106)^2-4(-16)(71)}}{2(-16)} &\mbox{}\\ \displaystyle &\displaystyle= \frac{-106\pm\sqrt{15780}}{-32}&\mbox{}\\ \end{array} $$ So, $$ t=\frac{-106+\sqrt{15780}}{-32}\approx -0.6130771869\,\,\,\,\mbox{}\,\,\,\,t=\frac{-106-\sqrt{15780}}{-32}\approx 7.238077187 $$ Since the negative time doesn't make sense, we conclude that the potato landed about $7.24$ seconds after firing.
(b) The potato will reach $114$ feet when $h(t)=114,$ that is, when $-16t^2 + 106t + 71=114.$
The resulting equation is $-16t^2 + 106t - 43=0,$ so that $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-(106)\pm\sqrt{(106)^2-4(-16)(-43)}}{2(-16)} &\mbox{}\\ \displaystyle &\displaystyle= \frac{-106\pm\sqrt{8484}}{-32}&\mbox{}\\ \end{array} $$ So, $$ t=\frac{-106+\sqrt{8484}}{-32}\approx 0.4341052651\,\,\,\,\mbox{}\,\,\,\,t=\frac{-106-\sqrt{8484}}{-32}\approx 6.190894735 $$ The potato will reach a height of $114$ at about $0.43$ seconds and $6.19$ seconds after firing.
For giggles, here is a graph of the height of the potato versus time.
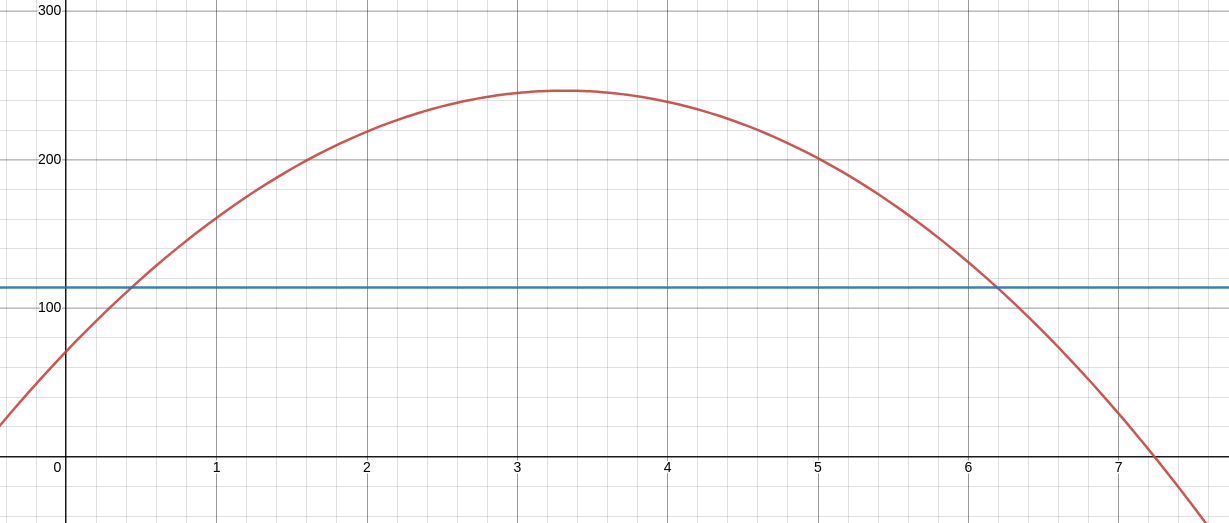
We then have $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-(106)\pm\sqrt{(106)^2-4(-16)(71)}}{2(-16)} &\mbox{}\\ \displaystyle &\displaystyle= \frac{-106\pm\sqrt{15780}}{-32}&\mbox{}\\ \end{array} $$ So, $$ t=\frac{-106+\sqrt{15780}}{-32}\approx -0.6130771869\,\,\,\,\mbox{}\,\,\,\,t=\frac{-106-\sqrt{15780}}{-32}\approx 7.238077187 $$ Since the negative time doesn't make sense, we conclude that the potato landed about $7.24$ seconds after firing.
(b) The potato will reach $114$ feet when $h(t)=114,$ that is, when $-16t^2 + 106t + 71=114.$
The resulting equation is $-16t^2 + 106t - 43=0,$ so that $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-(106)\pm\sqrt{(106)^2-4(-16)(-43)}}{2(-16)} &\mbox{}\\ \displaystyle &\displaystyle= \frac{-106\pm\sqrt{8484}}{-32}&\mbox{}\\ \end{array} $$ So, $$ t=\frac{-106+\sqrt{8484}}{-32}\approx 0.4341052651\,\,\,\,\mbox{}\,\,\,\,t=\frac{-106-\sqrt{8484}}{-32}\approx 6.190894735 $$ The potato will reach a height of $114$ at about $0.43$ seconds and $6.19$ seconds after firing.
For giggles, here is a graph of the height of the potato versus time.

Projectile Motion with Air Resistance
To account for air resistance at higher velocities requires more advanced mathematics.
That being said, the tools we have put into our chest today are the basic building blocks of more advanced modelling problems.
An Honest-to-Goodness Application
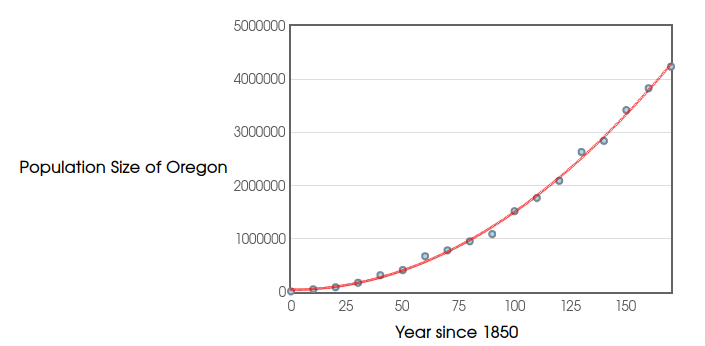
Below is a graph of the population of the state of Oregon since $1850.$

An Honest-to-Goodness Application
Fitting a quadratic equation to this data we have $$y=147.3072x^{2}-113.5297x+43724.5175$$
An Honest-to-Goodness Application
To estimate the population of Oregon using this expression at $x=150$ years after $1850$ (the year $2000$). Then, $$ \begin{array}{rll} y &=147.3072(\color{magenta}{150})^{2}-113.5297(\color{magenta}{150})+43724.5175&\mbox{}\\ &=147.3072(22500)-17029.455+43724.5175&\mbox{}\\ &=3314412+26695.0625&\mbox{}\\ &=3341107.0625&\mbox{}\\ \end{array} $$
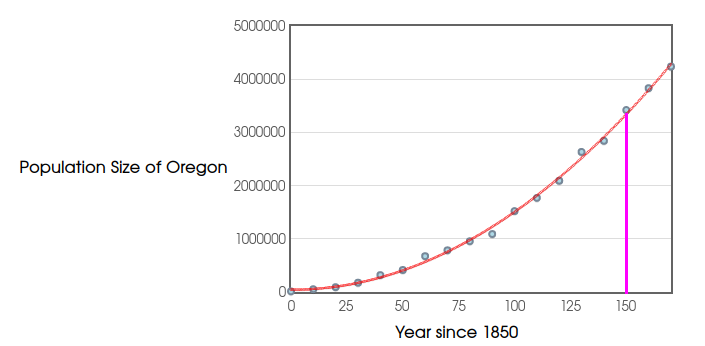
An Honest-to-Goodness Application
Our estimate, $\mbox{3,341,107},$ compares favorably to the true value of $\mbox{3,421,399}.$
The estimate comes in within $2.3\%$ of the true value.

Is anyone here interested in what the model predicts about the population of Oregon in $2030?$

An Honest-to-Goodness Application
Estimate the population of Oregon using the expression at $x=180$ (the year $2030$). $$ \begin{array}{rll} y &=147.3072(\color{magenta}{180})^{2}-113.5297(\color{magenta}{180})+43724.5175&\mbox{}\\ &=147.3072(32400)-20435.346+43724.5175&\mbox{}\\ &=4772753.28+23289.1715&\mbox{}\\ &=4796042.4515&\mbox{}\\ \end{array} $$ That is, we anticipate that about $\mbox{4,796,042},$ people will be living in Oregon by $2030.$
Big Question: When will Oregon's population reach $5$ million?
The question is, for what value of $x$ will the expression $\color{red}{y=147.3072x^{2}-113.5297x+43724.5175}$ equal $\mbox{5,000,000}?$

That is, solve the quadratic equation $$ \begin{array}{lll} \displaystyle y=147.3072x^{2}-113.5297x+43724.5175&\displaystyle=\mbox{5,000,000} &\mbox{}\\ \end{array} $$ or $$ 147.3072x^2-113.5297x-\mbox{4,956,275.4825}=0 $$ Using quadratic formula, $$ x=\frac{-(-113.5297)\pm\sqrt{(-113.5297)^2-4(147.3072)(-\mbox{4,956,275.4825})}}{2(147.3072)} $$ which gives $$ x \approx-183.0430972 \,\,\,\,\mbox{ OR }\,\,\,\, x\approx 183.8137975 $$ Discarding the negative root (our model doesn't work for times before $1850$), we have $$ x\approx 183.8137975 \mbox{ years after 1850} $$ That is, we estimate that Oregon's population will hit $5$ million in mid to late $2033.$

That is, solve the quadratic equation $$ \begin{array}{lll} \displaystyle y=147.3072x^{2}-113.5297x+43724.5175&\displaystyle=\mbox{5,000,000} &\mbox{}\\ \end{array} $$ or $$ 147.3072x^2-113.5297x-\mbox{4,956,275.4825}=0 $$ Using quadratic formula, $$ x=\frac{-(-113.5297)\pm\sqrt{(-113.5297)^2-4(147.3072)(-\mbox{4,956,275.4825})}}{2(147.3072)} $$ which gives $$ x \approx-183.0430972 \,\,\,\,\mbox{ OR }\,\,\,\, x\approx 183.8137975 $$ Discarding the negative root (our model doesn't work for times before $1850$), we have $$ x\approx 183.8137975 \mbox{ years after 1850} $$ That is, we estimate that Oregon's population will hit $5$ million in mid to late $2033.$