A Generic Quadratic Equation $ax^2+bx+c=0.$
We are going to solve this equation in general.
But first...
...we explore the human side of this formula.
Babylonian Mathematics
Babylon was a mathematically hip society. In particular, by the year $2000$ BCE, they had a positional base-$60$ number system (like our base-$10$ system) and, interestingly enough, had learned to solve quadratic equations.
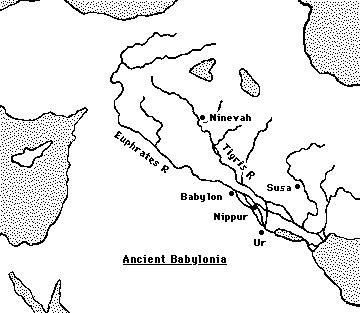
Babylonian Mathematics
Fun Fact: In $2000$ BCE the Babylonians were using a base-$60$ positional number system (much like our base-$10$ system) before Roman numerals were even invented!
Below are the $59$ symbols the Babylonians used in their system:
Example: Converting a Babylonian base-$60$ number to our base-$10$ system.
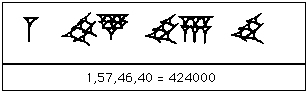
Question
How do we know all of this?
Answer
The Babylonians adopted from the Sumerians a style of writing on clay tablets cuneiform.
Babylonian Mathematics
Many of the tablets concern topics which, although mundane, nevertheless are historically fascinating. For example irrigation systems of the early civilizations in Mesopotamia were of critical importance. Of this Muroi writes:
It was an important task for the rulers of Mesopotamia to dig canals and to maintain them, because canals were not only necessary for irrigation but also useful for the transport of goods and armies. The rulers or high government officials must have ordered Babylonian mathematicians to calculate the number of workers and days necessary for the building of a canal, and to calculate the total expenses of wages of the workers.
Babylonian Mathematics
Thus, problems of length, area, and volume were critical to building and maintaining their civilization.
Here's a problem a scribe wrote in an ancient cuneiform tablet:
The area of a rectangle is
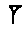$\mbox{[understood to be 1,0 or 60 in base-10 notation]}$
and its length exceeds its breadth by
$\mbox{[7]}.$
Solution: Compute half of
$\mbox{[7]}$,
namely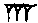 
$\mbox{[or 3; 30 using ; as the base-60 decimal point],}$ square it to get
$\mbox{[or 12; 15]}$.
To this add 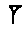$\mbox{[or 1, 0]}$ to get
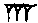
$\mbox{[1; 12, 15]}$.
Take its square root (from a table of squares) to get
$\mbox{[8; 30]}$.
From this subtract 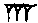$\mbox{[3; 30]}$
to give the answer 
$\mbox{[5]}$.
Question: Can anyone say what process this scribe writing about?
We are now going to solve $ax^2+bx+c=0$ in general.
$\displaystyle ax^2+bx=-c$
$\displaystyle x^2+\frac{b}{a}x=-\frac{c}{a}$
$\displaystyle x^2+\frac{b}{a}x+\left(\color{blue}{\frac{b}{2a}}\right)^2 =-\frac{c}{a}+\left(\color{blue}{\frac{b}{2a}}\right)^2$
$\displaystyle \left(x \color{blue}{+\frac{b}{2a}}\right)^2=-\frac{4ac}{4a^2}+\frac{b^2}{4a^2}$
$\displaystyle \left(x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$
$\displaystyle x+\frac{b}{2a}=\pm \sqrt{\frac{b^2-4ac}{4a^2}}$
$\displaystyle x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}$
$\displaystyle x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}$
$\displaystyle x=-\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a}$
When all is said and done, we have $$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}.$$ This is the quadratic formula.
Example Using the quadratic formula, solve the ancient area problem which the Babylonian scribe posed above.
That is, using our base-$10$ notation, solve $$x^2+7x=60.$$
Rewriting the equation in standard form, we have
$$
x^2+7x-60=0
$$
So, for this equation, $a=1,$ $b=7,$ and $c=-60.$
Then $$ \begin{array}{lll} \displaystyle x&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(7)\pm \sqrt{(7)^2-4(1)(-60)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm \sqrt{49+240}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm \sqrt{289}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm 17}{2} &\mbox{}\\ \end{array} $$ We then have $$ x=\frac{-7+ 17}{2}=5\,\,\,\,\mbox{or}\,\,\,\, x=\frac{-7-17}{2}=-12 $$
Then $$ \begin{array}{lll} \displaystyle x&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(7)\pm \sqrt{(7)^2-4(1)(-60)}}{2(1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm \sqrt{49+240}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm \sqrt{289}}{2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-7\pm 17}{2} &\mbox{}\\ \end{array} $$ We then have $$ x=\frac{-7+ 17}{2}=5\,\,\,\,\mbox{or}\,\,\,\, x=\frac{-7-17}{2}=-12 $$
Example: Solve the quadratic equation and completely simplify your answer. $$8v^2-12v-3=0$$
$$
\begin{array}{lll}
\displaystyle v&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-(-12)\pm \sqrt{(-12)^2-4(8)(-3)}}{2(8)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{12\pm \sqrt{144+96}}{16} &\mbox{}\\
\displaystyle &\displaystyle=\frac{12\pm \sqrt{240}}{16} &\mbox{}\\
\displaystyle &\displaystyle=\frac{12\pm 4\sqrt{15}}{16} &\mbox{simplify radical}\\
\displaystyle &\displaystyle=\frac{\color{magenta}{4}(3\pm \sqrt{15})}{\color{magenta}{4}\cdot 4} &\mbox{}\\
\displaystyle &\displaystyle=\frac{3\pm \sqrt{15}}{4} &\mbox{cancel common factors}\\
\end{array}
$$
So,
$$
v=\frac{3+ \sqrt{15}}{4}\approx 1.718245837\,\,\,\,\mbox{or}\,\,\,\, v=\frac{3- \sqrt{15}}{4}\approx -0.2182458366
$$
Examples: Use the quadratic formula to solve each quadratic equation.
$9q^2=-6q+5$
Getting into standard form, $9q^2+6q-5=0.$
Then $$ \begin{array}{lll} \displaystyle q&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(6)\pm \sqrt{(6)^2-4(9)(-5)}}{2(9)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm \sqrt{36+180}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm \sqrt{216}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 6\sqrt{6}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\color{magenta}{6}(-1\pm \sqrt{6})}{\color{magenta}{6} \cdot 3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-1\pm \sqrt{6}}{3} &\mbox{cancel common factors}\\ \end{array} $$ So $$ q=\frac{-1+ \sqrt{6}}{3}\approx 0.4831632476\,\,\,\,\mbox{or}\,\,\,\, q=\frac{-1- \sqrt{6}}{3}\approx -1.149829914 $$
Then $$ \begin{array}{lll} \displaystyle q&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(6)\pm \sqrt{(6)^2-4(9)(-5)}}{2(9)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm \sqrt{36+180}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm \sqrt{216}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-6\pm 6\sqrt{6}}{18} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\color{magenta}{6}(-1\pm \sqrt{6})}{\color{magenta}{6} \cdot 3} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-1\pm \sqrt{6}}{3} &\mbox{cancel common factors}\\ \end{array} $$ So $$ q=\frac{-1+ \sqrt{6}}{3}\approx 0.4831632476\,\,\,\,\mbox{or}\,\,\,\, q=\frac{-1- \sqrt{6}}{3}\approx -1.149829914 $$
$9x^2+12x+4=0$
$$
\begin{array}{lll}
\displaystyle x&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-(12)\pm \sqrt{(12)^2-4(9)(4)}}{2(9)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-12\pm \sqrt{144-144}}{18} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-12\pm \sqrt{0}}{18} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-12\pm 0}{18} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-12}{18} &\mbox{}\\
\displaystyle &\displaystyle=-\frac{2}{3} &\mbox{}\\
\end{array}
$$
$4t^2-4t=-9$
Getting into standard form, $4t^2-4t+9=0.$
Then $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(-4)\pm \sqrt{(-4)^2-4(4)(9)}}{2(4)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4 \pm \sqrt{16-144}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm \sqrt{-128}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm 8i\sqrt{2}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\color{magenta}{4}(1\pm 2i\sqrt{2})}{\color{magenta}{4} \cdot 2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1\pm 2i\sqrt{8}}{2} &\mbox{cancel common factors}\\ \displaystyle &\displaystyle=\frac{1}{2}\pm i\sqrt{8} &\mbox{}\\ \end{array} $$ So $$ t=\frac{1}{2}+ i\sqrt{8}\approx 0.5+1.414213562i\,\,\,\,\mbox{or}\,\,\,\, t=\frac{1}{2}- i\sqrt{8}\approx 0.5-1.414213562i $$
Then $$ \begin{array}{lll} \displaystyle t&\displaystyle=\frac{-b\pm \sqrt{b^2-4ac}}{2a} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(-4)\pm \sqrt{(-4)^2-4(4)(9)}}{2(4)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4 \pm \sqrt{16-144}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm \sqrt{-128}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{4\pm 8i\sqrt{2}}{8} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\color{magenta}{4}(1\pm 2i\sqrt{2})}{\color{magenta}{4} \cdot 2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1\pm 2i\sqrt{8}}{2} &\mbox{cancel common factors}\\ \displaystyle &\displaystyle=\frac{1}{2}\pm i\sqrt{8} &\mbox{}\\ \end{array} $$ So $$ t=\frac{1}{2}+ i\sqrt{8}\approx 0.5+1.414213562i\,\,\,\,\mbox{or}\,\,\,\, t=\frac{1}{2}- i\sqrt{8}\approx 0.5-1.414213562i $$
Question
Is there an easier way to determine the number of solutions to a quadratic equation?
Answer
Yes! We can use the discriminant to determine the number of solutions a quadratic equations has.
Another Question
What is the discriminant? D;
Another Answer
The discriminant is simply the quantity $b^2-4ac$. This is the stuff under the square-root sign in the quadratic formula.
If $b^2-4ac>0$, then $ax^2+bx+c=0$ has $2$ real number solutions.
If $b^2-4ac=0$, then $ax^2+bx+c=0$ has $1$ solution.
If $b^2-4ac<0$, then $ax^2+bx+c=0$ has $0$ real number solutions (that is, $2$ complex solutions).
Example: How many real number solutions does each quadratic equation have?
$9q^2=-6q+5$
In standard form we have, $9q^2+6q-5=0.$
Since, $b^2-4ac=(6)^2-4(9)(-5)=36+180=216 \gt 0,$ the equation has $2$ real solutions.
Since, $b^2-4ac=(6)^2-4(9)(-5)=36+180=216 \gt 0,$ the equation has $2$ real solutions.
$9x^2+12x+4=0$
Since, $b^2-4ac=(12)^2-4(9)(4)=144-144= 0,$ the equation has $1$ solution.
$4t^2-4t=-9$
In standard form we have, $4t^2-4t+9=0.$
Since, $b^2-4ac=(-4)^2-4(4)(9)=16-144=-128 \lt 0,$ the equation has $0$ real solutions (that is, $2$ complex solutions).
Since, $b^2-4ac=(-4)^2-4(4)(9)=16-144=-128 \lt 0,$ the equation has $0$ real solutions (that is, $2$ complex solutions).
If There's Time: Bonus Application
The height in meters of a ball released from a ramp is given by the function $h(t)=-4.9t^2+23t+31,$ where $t$ represents the time in seconds since the ball was released from the end of the ramp.
How many seconds will it take for the ball to hit the ground?
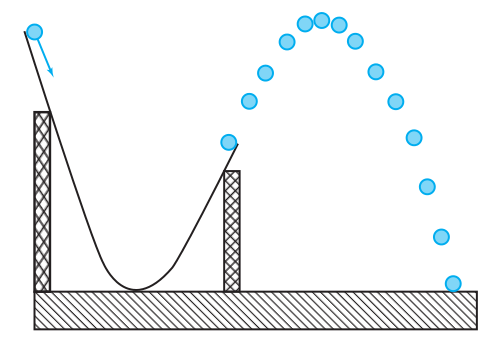
The ball will hit the ground when the height $h$ is $0.$
Therefore, we must solve the equation $h(t)=0$ which gives $$ \begin{array}{lll} &\displaystyle -4.9t^2+23t+31=0&\mbox{}\\ \implies &\displaystyle t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}&\mbox{}\\ \implies &\displaystyle t=\frac{-(23)\pm \sqrt{(23)^2-4(-4.9)(31)}}{2(-4.9)}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{529+607.6}}{-9.8}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{1136.6}}{-9.8}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{1136.6}}{-9.8}&\mbox{}\\ \end{array} $$ So $$ t=\frac{-23+ \sqrt{1136.6}}{-9.8}\approx -1.093214161\,\,\,\,\mbox{or}\,\,\,\, t=\frac{-23- \sqrt{1136.6}}{-9.8}\approx 5.787091712 $$ We discard the negative root since a negative time does not make sense.
Thus, the ball will hit the ground after approximately $5.8$ seconds of flight.
Therefore, we must solve the equation $h(t)=0$ which gives $$ \begin{array}{lll} &\displaystyle -4.9t^2+23t+31=0&\mbox{}\\ \implies &\displaystyle t=\frac{-b\pm \sqrt{b^2-4ac}}{2a}&\mbox{}\\ \implies &\displaystyle t=\frac{-(23)\pm \sqrt{(23)^2-4(-4.9)(31)}}{2(-4.9)}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{529+607.6}}{-9.8}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{1136.6}}{-9.8}&\mbox{}\\ \implies &\displaystyle t=\frac{-23\pm \sqrt{1136.6}}{-9.8}&\mbox{}\\ \end{array} $$ So $$ t=\frac{-23+ \sqrt{1136.6}}{-9.8}\approx -1.093214161\,\,\,\,\mbox{or}\,\,\,\, t=\frac{-23- \sqrt{1136.6}}{-9.8}\approx 5.787091712 $$ We discard the negative root since a negative time does not make sense.
Thus, the ball will hit the ground after approximately $5.8$ seconds of flight.
