Let's start off with something "easy."
Factor the expression $x^2+6x+9$.
A Little More Difficult
What do we need to add to the expression $$x^2+6x+\mbox{_____}$$ to make it into a perfect square trinomial?
Visualizing Completing the Square: $x^2+6x+\mbox{_____}$
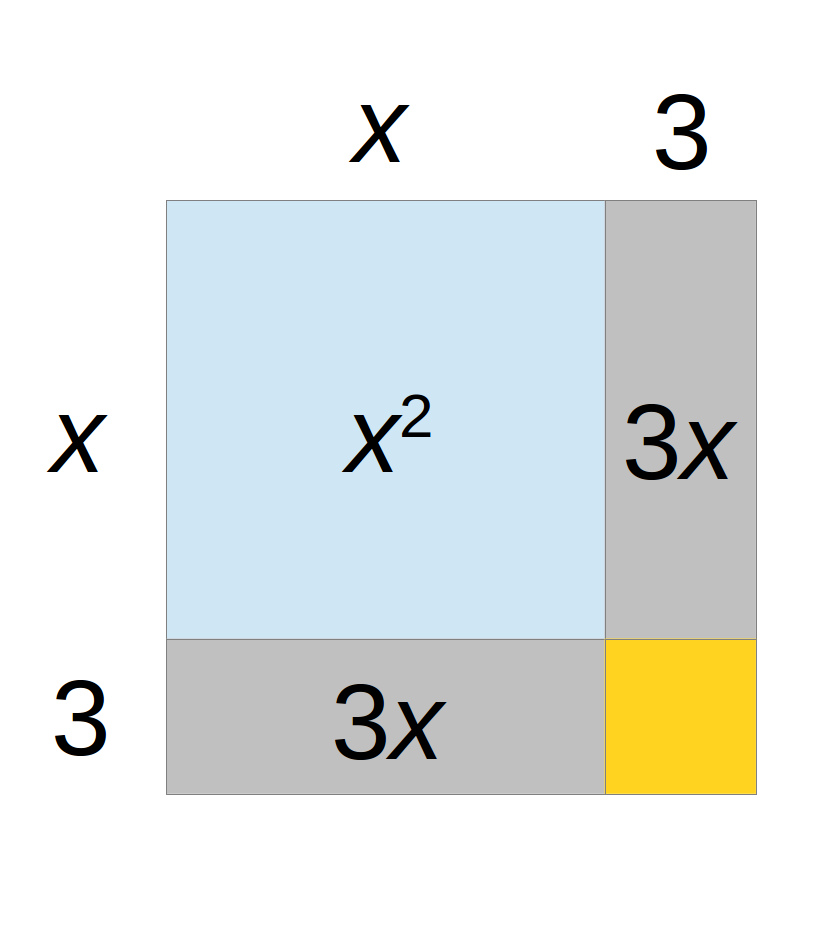
Completing the Square in General
Question: What number do I need to add to $x^2+bx$ to get a perfect square?
Answer: $\displaystyle \left(\frac{b}{2}\right)^2$
Example: What number goes in the blank to make a perfect square? $x^2+6x+\mbox{_____}$
Visualizing Completing the Square: $x^2+bx+\mbox{_____}$
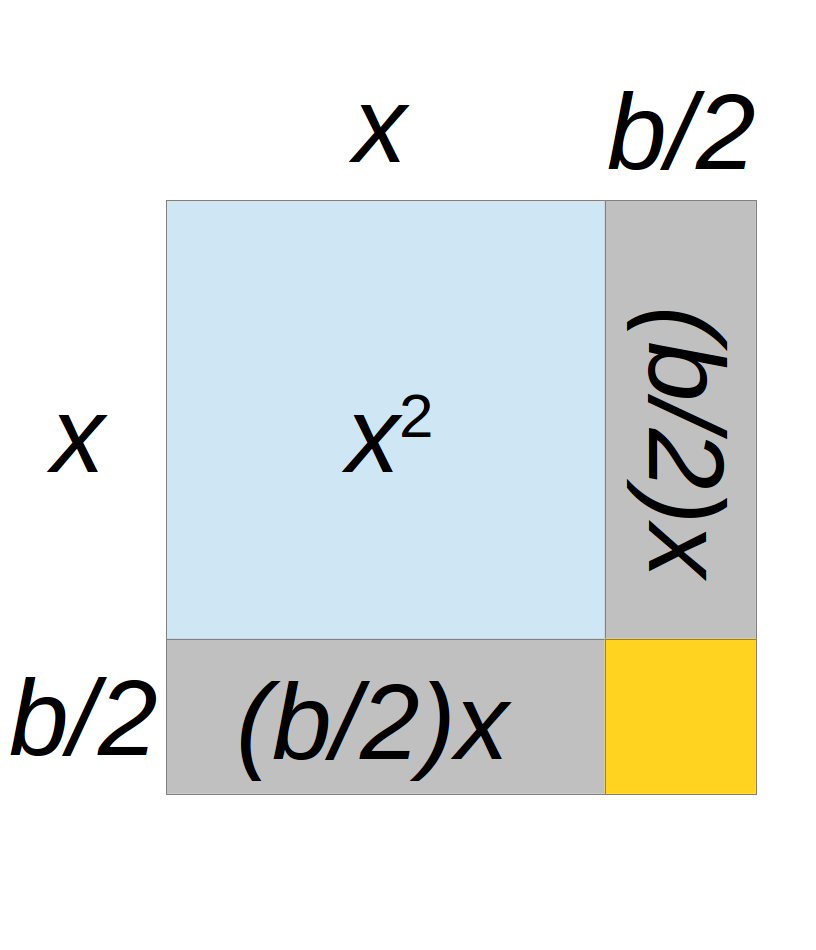
Examples: Complete the square.
$x^2+4x$
$\displaystyle x^2+\color{magenta}{4}x\underbrace{+\left(\frac{\color{magenta}{4}}{2}\right)^2}_{adding\\this\\term\\completes\\square}=\left(x+\frac{\color{magenta}{4}}{2}\right)^2=(x+2)^2$
$x^2-5x$
$\displaystyle x^2\color{magenta}{-5}x+\underbrace{\left(\color{magenta}{-}\frac{\color{magenta}{5}}{2}\right)^2}_{adding\\this\\term\\completes\\square}=\left(x\color{magenta}{-}\frac{\color{magenta}{5}}{2}\right)^2$
$\displaystyle x^2+\frac{3}{2}x$
$\displaystyle x^2+\color{magenta}{\frac{3}{2}}x\underbrace{+\left(\frac{\color{magenta}{3/2}}{2}\right)^2}_{adding\\this\\term\\completes\\square}=\left(x+\frac{\color{magenta}{3/2}}{2}\right)^2=\left(x+\frac{3}{4}\right)^2$
$\displaystyle x^2-\frac{1}{4}x$
$\displaystyle x^2\color{magenta}{-\frac{1}{4}}x+\underbrace{\left(\color{magenta}{-}\frac{\color{magenta}{1/4}}{2}\right)^2}_{adding\\this\\term\\completes\\square}=\left(x\color{magenta}{-}\frac{\color{magenta}{1/4}}{2}\right)^2=\left(x-\frac{1}{8}\right)^2$
And what is our reward for going to all this trouble to learn how to complete the square? ...
Answer: You guessed it! We get to solve more equations! :D

In fact we can now solve any quadratic equation! (Whether it's factorable or not.)
Example: Solve the quadratic equation $x^2+3x-1=0$
$$
\begin{array}{lll}
&\displaystyle x^2+3x-1=0 &\mbox{}\\
\implies &\displaystyle x^2+3x-1\color{blue}{+1}=0\color{blue}{+1}&\mbox{}\\
\implies &\displaystyle x^2+3x=1&\mbox{}\\
\implies &\displaystyle x^2+\color{magenta}{3}x\color{blue}{+\left(\frac{\color{magenta}{3}}{2}\right)^2}=1\color{blue}{+\left(\frac{\color{magenta}{3}}{2}\right)^2}&\mbox{complete the square on LHS}\\
\implies &\displaystyle \left(x+\frac{\color{magenta}{3}}{2}\right)^2=1+\frac{9}{4}&\mbox{}\\
\implies &\displaystyle \left(x+\frac{\color{magenta}{3}}{2}\right)^2=\frac{13}{4}&\mbox{}\\
\implies &\displaystyle x+\frac{3}{2}=\pm\sqrt{\frac{13}{4}}&\mbox{by the square root property!}\\
\implies &\displaystyle x+\frac{3}{2}=\pm\frac{\sqrt{13}}{2}&\mbox{simplify radical}\\
\implies &\displaystyle x+\frac{3}{2}\color{blue}{-\frac{3}{2}}=\pm\frac{\sqrt{13}}{2}\color{blue}{-\frac{3}{2}}&\mbox{}\\
\implies &\displaystyle x=-\frac{3}{2}\pm\frac{\sqrt{13}}{2}&\mbox{}\\
\implies &\displaystyle x=\frac{-3\pm\sqrt{13}}{2}&\mbox{}\\
\end{array}
$$
Special Note: The homework will ask you to not simplify the radical expression.
The correct option in this case would look like
$$x=\displaystyle -\frac{3}{2}\pm\sqrt{\frac{13}{4}}$$
Another Example: Solve the quadratic equation $$3x^2+x-1=0.$$
$$
\begin{array}{lll}
&\displaystyle 3x^2+x-1=0 &\mbox{}\\
\implies &\displaystyle \frac{3x^2}{\color{blue}{3}}+\frac{x}{\color{blue}{3}}-\frac{1}{\color{blue}{3}}=\frac{0}{\color{blue}{3}}&\mbox{}\\
\implies &\displaystyle x^2+\frac{1}{3}x-\frac{1}{3}=0&\mbox{}\\
\implies &\displaystyle x^2+\frac{1}{3}x-\frac{1}{3}\color{blue}{+\frac{1}{3}}=0\color{blue}{+\frac{1}{3}}&\mbox{}\\
\implies &\displaystyle x^2+\frac{1}{3}x=\frac{1}{3}&\mbox{}\\
\implies &\displaystyle x^2+\color{magenta}{\frac{1}{3}}x\color{blue}{+\left(\frac{\color{magenta}{1/3}}{2}\right)^2}=\frac{1}{3}\color{blue}{+\left(\frac{\color{magenta}{1/3}}{2}\right)^2}&\mbox{}\\
\implies &\displaystyle \left(x+\frac{\color{magenta}{1/3}}{2}\right)^2=\frac{1}{3}+\left(\frac{1/3}{2}\right)^2&\mbox{complete square on LHS}\\
\implies &\displaystyle \left(x+\frac{1}{6}\right)^2=\frac{1}{3}+\left(\frac{1}{6}\right)^2&\mbox{}\\
\implies &\displaystyle \left(x+\frac{1}{6}\right)^2=\frac{1}{3}+\frac{1}{36}&\mbox{}\\
\implies &\displaystyle \left(x+\frac{1}{6}\right)^2=\frac{13}{36}&\mbox{}\\
\implies &\displaystyle x+\frac{1}{6}=\pm\sqrt{\frac{13}{36}}&\mbox{by the square root property}\\
\implies &\displaystyle x+\frac{1}{6}=\pm\frac{\sqrt{13}}{6}&\mbox{simplify radical}\\
\implies &\displaystyle x+\frac{1}{6}\color{blue}{-\frac{1}{6}}=\pm\frac{\sqrt{13}}{6}\color{blue}{-\frac{1}{6}}&\mbox{}\\
\implies &\displaystyle x=-\frac{1}{6}\pm\frac{\sqrt{13}}{6}&\mbox{}\\
\implies &\displaystyle x=\frac{-1\pm\sqrt{13}}{6}&\mbox{}\\
\end{array}
$$
Special Note: The homework will ask you to not simplify the radical expression.
The correct option in this case would look like
$$x=\displaystyle -\frac{1}{6}\pm\sqrt{\frac{13}{36}}$$
The Moral of the Story
Completing the square works only with $x^2+bx$.
How to Solve any Quadratic Equation: $Ax^2+Bx+C=0$
Step 0: Divide out any GCFs if necessary.
Step 1: Get your equation into the form $Ax^2+Bx=-C$.
Step 2: Divide both sides by $A$ to get an expression of the form $$x^2+bx=\mbox{some number}$$ Step 3: Add $\displaystyle \left(\frac{b}{2}\right)^2$ to both sides $x^2+bx$ into a perfect square. (Complete the Square!)
Step 4: You should then have an equation of the form $$\left(x+\frac{b}{2}\right)^2=\mbox{another number}$$ which is easy to solve. (Use the Square Root Property from last time.)
Examples: Solve each quadratic equation by completing the square.
$9 x^2-117 x-171=0$
$$
\begin{array}{lll}
&\displaystyle 9 x^2-117 x-171=0&\mbox{}\\
\implies &\displaystyle x^2-13 x-19=0&\mbox{Step 0}\\
\implies &\displaystyle x^2-13 x=19&\mbox{Step 1 and Step 2}\\
\implies &\displaystyle x^2-13 x+\left(-\frac{13}{2}\right)^2=19+\left(-\frac{13}{2}\right)^2&\mbox{Step 3: Complete the Square!}\\
\implies &\displaystyle \left(x-\frac{13}{2}\right)^2=19+\frac{169}{4}&\mbox{}\\
\implies &\displaystyle \left(x-\frac{13}{2}\right)^2=\frac{245}{4}&\mbox{Step 4}\\
\implies &\displaystyle x-\frac{13}{2}=\pm\sqrt{\frac{245}{4}}&\mbox{}\\
\implies &\displaystyle x-\frac{13}{2}=\pm\frac{\sqrt{245}}{2}&\mbox{}\\
\implies &\displaystyle x-\frac{13}{2}=\pm\frac{7\sqrt{5}}{2}&\mbox{}\\
\implies &\displaystyle x=\frac{13}{2}\pm\frac{7\sqrt{5}}{2}&\mbox{}\\
\implies &\displaystyle x=\frac{13\pm 7\sqrt{5}}{2}&\mbox{}\\
\end{array}
$$
Special Note: The homework will ask you to not simplify the radical expression.
The correct option in this case would look like
$$x=\displaystyle \frac{13}{2}\pm\sqrt{\frac{245}{4}}$$
$9 t^2-3 t-7=0$
$$
\begin{array}{lll}
&\displaystyle 9 t^2-3 t-7=0 &\mbox{}\\
\implies &\displaystyle 9 t^2-3 t=7&\mbox{Step 1}\\
\implies &\displaystyle t^2-\frac{1}{3} t=\frac{7}{9}&\mbox{Step 2}\\
\implies &\displaystyle t^2-\frac{1}{3} t +\left(\frac{1}{6}\right)^2=\frac{7}{9}+\left(\frac{1}{6}\right)^2&\mbox{Step 3: Complete the Square!}\\
\implies &\displaystyle \left(t-\frac{1}{6}\right)^2=\frac{29}{36}&\mbox{Step 4}\\
\implies &\displaystyle t-\frac{1}{6}=\pm\sqrt{\frac{29}{36}}&\mbox{}\\
\implies &\displaystyle t-\frac{1}{6}=\pm\frac{\sqrt{29}}{6}&\mbox{}\\
\implies &\displaystyle t=\frac{1}{6}\pm\frac{\sqrt{29}}{6}&\mbox{}\\
\implies &\displaystyle t=\frac{1\pm\sqrt{29}}{6}&\mbox{}\\
\end{array}
$$
Special Note: The homework will ask you to not simplify the radical expression.
The correct option in this case would look like
$$t=\displaystyle \frac{1}{6}\pm\sqrt{\frac{29}{36}}$$