Today, we expand our horizons from the real numbers $\mathbb{R}$ to a new number system called the complex numbers.
The Motivation
Solve the equation $$x^2+1=0.$$
The Complex Numbers
Any complex number can be expressed as $$a+bi$$ where $a$ and $b$ are real numbers.
The complex numbers are denoted by the symbol $\mathbb{C}.$
Complex Arithmetic: Adding and Subtracting
Add: $(6-8i)+(-11-7i)$
$$
\begin{array}{lll}
\displaystyle (6-8i)+(-11-7i)&\displaystyle=6-11-8i-7i &\mbox{}\\
\displaystyle &\displaystyle=-5-15i &\mbox{}\\
\end{array}
$$
Subtract: $(-3-5i)-(-1+10i)$
$$
\begin{array}{lll}
\displaystyle (-3-5i)-(-1+10i)&\displaystyle=-3-5i+1-10i &\mbox{}\\
\displaystyle &\displaystyle=-3+1-5i-10i &\mbox{}\\
\displaystyle &\displaystyle=-2-15i &\mbox{}\\
\end{array}
$$
Complex Arithmetic: Multiplication
Multiply: $(-5+3i)(-8-2i)$
$$
\begin{array}{lll}
\displaystyle (-5+3i)(-8-2i)&\displaystyle=\overbrace{(-5)(-8)}^{\mbox{First}}+\overbrace{(-5)(-2i)}^{\mbox{Outer}}+\overbrace{(3i)(-8)}^{\mbox{Inner}}+\overbrace{(3i)(-2i)}^{\mbox{Last}} &\mbox{}\\
\displaystyle &\displaystyle=40+10i-24i-6i^2 &\mbox{}\\
\displaystyle &\displaystyle=40+10i-24i-6(-1) &\mbox{}\\
\displaystyle &\displaystyle=40+10i-24i+6 &\mbox{}\\
\displaystyle &\displaystyle=46-14i &\mbox{}\\
\end{array}
$$
Multiply: $(8-11i)(8+11i)$
$$
\begin{array}{lll}
\displaystyle (8-11i)(8+11i)&\displaystyle=\overbrace{8\cdot 8}^{\mbox{First}}+\overbrace{8\cdot 11i}^{\mbox{Outer}}+\overbrace{(-11i)\cdot 8}^{\mbox{Inner}}+\overbrace{(11i)(-11i)}^{\mbox{Last}} &\mbox{}\\
\displaystyle &\displaystyle=64+88i-88i-121i^2 &\mbox{}\\
\displaystyle &\displaystyle=64-121(-1) &\mbox{}\\
\displaystyle &\displaystyle=64+121 &\mbox{}\\
\displaystyle &\displaystyle=185 &\mbox{}\\
\end{array}
$$
Note: multiplying complex numbers is similar to the process of FOIL.
Complex Arithmetic: Exponents.
Example: $$(-1-11i)^2$$ Hint: expand the square and then FOIL.
$$
\begin{array}{lll}
\displaystyle (-1-11i)^2&\displaystyle=(-1-11i)(-1-11i) &\mbox{}\\
\displaystyle &\displaystyle=\overbrace{(-1)\cdot (-1)}^{\mbox{First}}+\overbrace{(-1)(-11i)}^{\mbox{Outer}}+\overbrace{(-11i)(-1)}^{\mbox{Inner}}+\overbrace{(-11i)(-11i)}^{\mbox{Last}} &\mbox{}\\
\displaystyle &\displaystyle=1+11i+11i+121i^2 &\mbox{}\\
\displaystyle &\displaystyle=1+22i+121(-1) &\mbox{}\\
\displaystyle &\displaystyle=1+22i-121 &\mbox{}\\
\displaystyle &\displaystyle=-120+22i &\mbox{}\\
\end{array}
$$
Complex Arithmetic: Powers of $i.$
Find the following powers of $i$:
$i^{98}$
$4$ divides into $98$ with a quotient of $24$ and a remainder of $\color{magenta}{2}.$
Thus, $i^{98}=i^{\color{magenta}{2}}=-1$
Thus, $i^{98}=i^{\color{magenta}{2}}=-1$
$i^{187}$
$4$ divides into $187$ with a quotient of $46$ and a remainder of $\color{magenta}{3}.$
Thus, $i^{187}=i^{\color{magenta}{3}}=-i$
Thus, $i^{187}=i^{\color{magenta}{3}}=-i$
$i^{-79}$
We first note that $\displaystyle i^{-79}=\frac{1}{i^{79}}.$
Since $4$ divides into $79$ with a quotient of $19$ and a remainder of $\color{magenta}{3},$ we have $$ i^{-79}=\frac{1}{i^{79}}=\frac{1}{i^{\color{magenta}{3}}}=\frac{1}{-i} $$ To deal with $-i$ in the denominator, we multiply by a fancy one. $$ \begin{array}{lll} \displaystyle i^{-79}&\displaystyle=\frac{1}{-i} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{-i} \color{\magenta}{\frac{i}{i}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{1\cdot i}{-i\cdot i}&\mbox{}\\ \displaystyle &\displaystyle=\frac{i}{-(-1)}&\mbox{}\\ \displaystyle &\displaystyle=\frac{i}{1}&\mbox{}\\ \displaystyle &\displaystyle=i&\mbox{}\\ \end{array} $$
Since $4$ divides into $79$ with a quotient of $19$ and a remainder of $\color{magenta}{3},$ we have $$ i^{-79}=\frac{1}{i^{79}}=\frac{1}{i^{\color{magenta}{3}}}=\frac{1}{-i} $$ To deal with $-i$ in the denominator, we multiply by a fancy one. $$ \begin{array}{lll} \displaystyle i^{-79}&\displaystyle=\frac{1}{-i} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{-i} \color{\magenta}{\frac{i}{i}}&\mbox{}\\ \displaystyle &\displaystyle=\frac{1\cdot i}{-i\cdot i}&\mbox{}\\ \displaystyle &\displaystyle=\frac{i}{-(-1)}&\mbox{}\\ \displaystyle &\displaystyle=\frac{i}{1}&\mbox{}\\ \displaystyle &\displaystyle=i&\mbox{}\\ \end{array} $$
Dividing Complex Numbers
Example: $$\frac{-3+2i}{7+11i}$$ Note: dividing complex numbers is similar to the process of rationalizing denominators.
$$
\begin{array}{lll}
\displaystyle\frac{-3+2i}{7+11i} &\displaystyle=\frac{-3+2i}{7+11i} \color{\magenta}{\frac{7-11i}{7-11i}}&\mbox{multiply by conjugate fancy one}\\
\displaystyle &\displaystyle=\frac{(-3+2i)(7-11i)}{(7+11i)(7-11i)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-21+33i+14i-22i^2}{49-77i+77i-121i^2} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-21+47i-22(-1)}{49-121(-1)} &\mbox{}\\
\displaystyle &\displaystyle=\frac{-21+47i+22}{49+121} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1+47i}{170} &\mbox{}\\
\displaystyle &\displaystyle=\frac{1}{170}+\frac{47}{170}i &\mbox{}\\
\end{array}
$$

Warning: Stop Taking Notes!
The Real Motivation: The complex numbers give the $xy$-plane an algebraic structure.
If we let the complex number $a+bi$ stand in as the ordered pair $(a,b),$ we get something very nice...

Complex Functions: When we consider functions on the complex plane $\mathbb{C}$, we get new kinds of geometry.
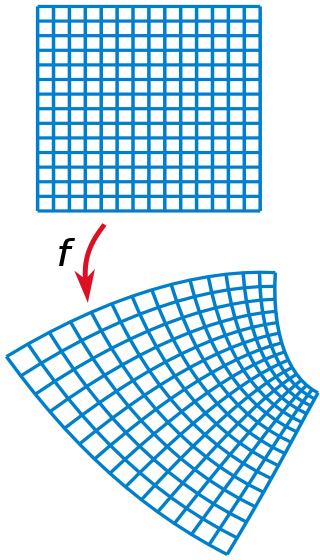
Complex Functions: When we consider functions on the complex plane $\mathbb{C}$, we get new kinds of geometry.
Complex Functions
This kind of geometry can describe how liquids and gases flow around an object.
For example, complex functions model the flow of an incompressible fluid around a cylinder.
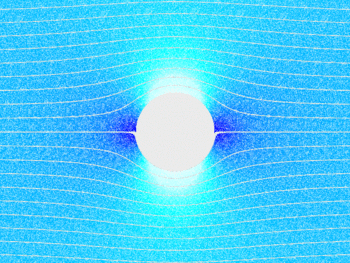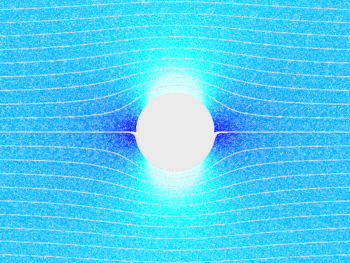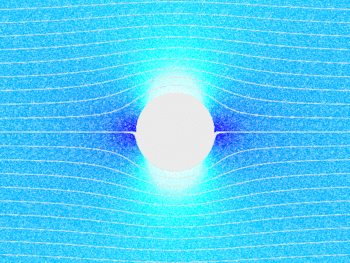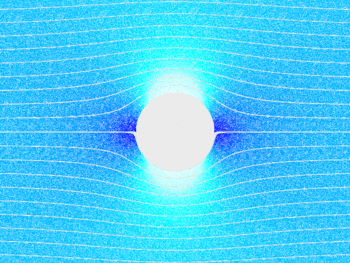
This is because certain complex functions by their very nature solve the kinds of equations which describe many different types of phenomena including fluid flow, temperature, and electricity & magnetism.
Another Fascinating Tidbit: Fractals
Consider the following sequence. Let $z_0=0$, and choose any complex number $a+bi$. Define a sequence of complex numbers by the following $$z_{n+1}=z_n^2+(a+bi).$$ $a+bi=$$\,+\,$$\,i\,$
The Making of an Intriguing Figure
If a number $a+bi$ gives us an "settle" sequence, make the point $a+bi$ in the complex plane blue.
If a number $a+bi$ gives us an "boom" sequence, make the point $a+bi$ in the complex plane pink.
Programming a computer to do this, we get the following figure...
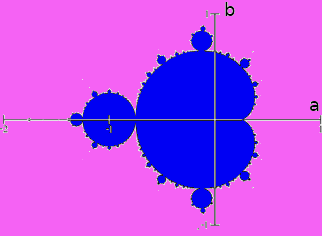
"settle" sequence "boom" sequence
Fractals
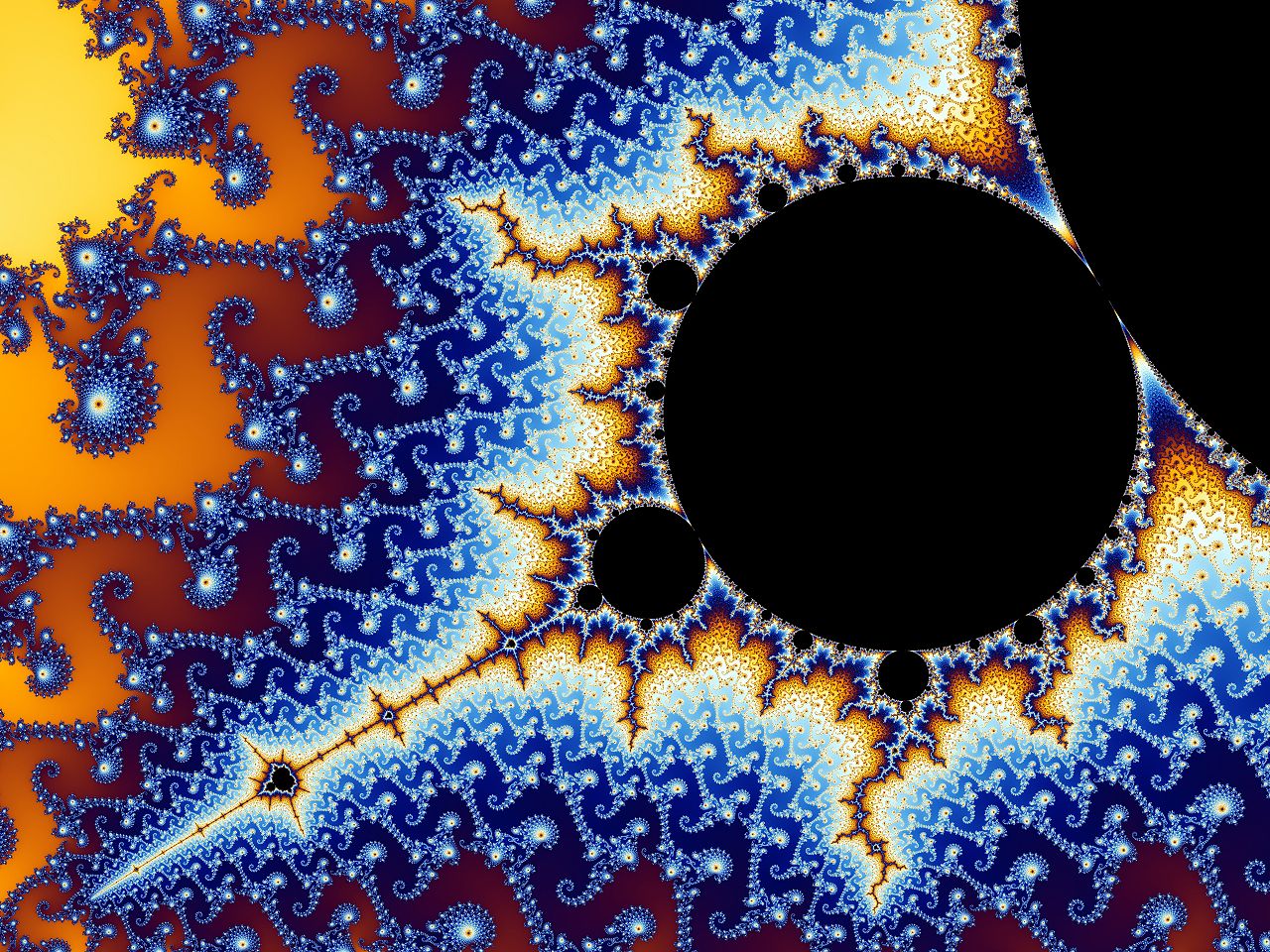
Roughly speaking, fractals are figures that repeat on an ever-diminishing scale.
As such, they have an infinite amount of detail.
Thus, we may zoom in on a fractal figure as much as we like, and the resulting figure will be as detailed as the original.
The Mandelbrot set is infinitely detailed since it is self similar at all scales.




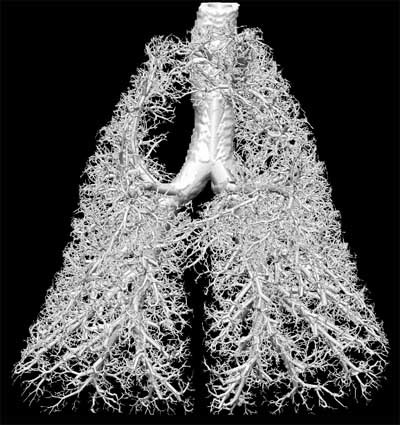
Self similarity occurs in many places in nature: trees, ferns, clouds, watersheds (river systems), physiology and many others.


Self similarity occurs in many places in nature: trees, ferns, clouds, watersheds (river systems), physiology and many others.


Self similarity occurs in many places in nature: trees, ferns, clouds, watersheds (river systems), physiology and many others.



Final Thought
As strange as the complex numbers may seem at first, they are the most natural completion of the real numbers.
At a certain level of mathematics, the tedious, complicated, annoying details one has to keep track of when working with real numbers all seem to magically disappear when we expand our view and embrace the complex numbers.
Quote of the Day: The shortest path between two truths in the real domain passes through the complex domain.
—Jacques Hadamard