Fact: Rational expressions have their own arithmetic (addition, subtraction, multiplication, and division).
Now that we know how to do arithmetic with rational expressions, we may now solve equations involving rational expressions.
Two Warm-Up Examples
$\displaystyle \frac{4}{t - 5}=\displaystyle \frac{2}{t + 3}$
$$
\begin{array}{lll}
&\displaystyle \frac{4}{t - 5}=\displaystyle \frac{2}{t + 3}&\mbox{}\\
\implies &\displaystyle \frac{4}{t - 5}\color{magenta}{(t-5)(t+3)}=\displaystyle \frac{2}{t + 3}\color{magenta}{(t-5)(t+3)}&\mbox{multiply each term by something which cancels all denoms}\\
\implies &\displaystyle 4\color{magenta}{(t+3)}=2\color{magenta}{(t-5)}&\mbox{cancel}\\
\implies &\displaystyle 4t+12=2t-10 &\mbox{distribute}\\
\implies &\displaystyle 4t+12\color{magenta}{-2t}\color{blue}{-12}=2t-10\color{magenta}{-2t}\color{blue}{-12} &\mbox{subtract $2t$ and 12 from both sides}\\
\implies &\displaystyle 2t=-22&\mbox{simplify}\\
\implies &\displaystyle \frac{2t}{\color{magenta}{2}}=\frac{-22}{\color{magenta}{2}}&\mbox{divide both sides by 2}\\
\implies &\displaystyle t=-11&\mbox{simplify}\\
\end{array}
$$
$\displaystyle \frac{1}{h + 3}-5=\displaystyle \frac{1}{h + 3}$
$$
\begin{array}{lll}
&\displaystyle \frac{1}{h + 3}-5= \frac{1}{h + 3}&\mbox{}\\
\implies &\displaystyle\frac{1}{h + 3}\color{magenta}{(h+3)}-5\color{magenta}{(h+3)}= \frac{1}{h + 3}\color{magenta}{(h+3)}&\mbox{multiply both sides by something which cancels all denoms}\\
\implies &\displaystyle 1-5(h+3)=1&\mbox{cancel}\\
\implies &\displaystyle 1-5h-15=1 &\mbox{distribute}\\
\implies &\displaystyle -5h-14=1 &\mbox{simplify}\\
\implies &\displaystyle -5h-14\color{magenta}{+14}=1\color{magenta}{+14} &\mbox{add 14 to both sides}\\
\implies &\displaystyle -5h=15&\mbox{simplify}\\
\implies &\displaystyle \frac{-5h}{\color{magenta}{-5}}=\frac{15}{\color{magenta}{-5}}&\mbox{divide both sides by $-5$}\\
\implies &\displaystyle h=-3&\mbox{simplify}\\
\end{array}
$$
Since $h=-3$ results in zero denominators, this equation has no solution.
Solving Equations with Rational Expression
Process: To solve an equation with rational expressions:
1) Multiply every term by something which cancels all the denominators.
2) Solve the resulting fraction-less equation.
3) Check for extraneous (fake) solutions.
Examples
$\displaystyle \frac{ a}{a^2+7 a - 18}-\displaystyle \frac{ a}{a^2 +17 a + 72}=\displaystyle \frac{4 a}{a^2+6 a - 16}$ (two bonafide solutions)
$$
\begin{array}{lll}
&\displaystyle \frac{ a}{a^2+7 a - 18}-\frac{ a}{a^2 +17 a + 72}= \frac{4 a}{a^2+6 a - 16}&\mbox{}\\
\implies &\displaystyle \frac{ a}{(a-2)(a+9)}-\frac{ a}{(a+8)(a+9)}=\frac{4 a}{(a-2)(a+8)}&\mbox{factor all denominators}\\
\implies &\displaystyle \frac{ a}{(a-2)(a+9)}\color{magenta}{(a-2)(a+9)(a+8)}-\frac{ a}{(a+8)(a+9)}\color{magenta}{(a-2)(a+9)(a+8)}=\frac{4 a}{(a-2)(a+8)}\color{magenta}{(a-2)(a+9)(a+8)} &\mbox{multiply by special factor}\\
\implies &\displaystyle a\color{magenta}{(a+8)}-a\color{magenta}{(a-2)}=4 a\color{magenta}{(a+9)} &\mbox{cancel common factors}\\
\implies &\displaystyle a^2+8a-a^2+2a=4a^2+36a &\mbox{distribute}\\
\implies &\displaystyle 10a=4a^2+36a &\mbox{simplify}\\
\implies &\displaystyle 10a\color{magenta}{-10a}=4a^2+36a \color{magenta}{-10a}&\mbox{subtract $10a$ from both sides}\\
\implies &\displaystyle 0=4a^2+26a&\mbox{simplify}\\
\implies &\displaystyle 0=2a(2a+13)&\mbox{factor}\\
\implies &\displaystyle a=0 \,\,\,\,\mbox{or}\,\,\,\,2a+13=0&\mbox{zero factor property}\\
\implies &\displaystyle a=0 \,\,\,\,\mbox{or}\,\,\,\,a=-\frac{13}{2}&\mbox{}\\
\end{array}
$$
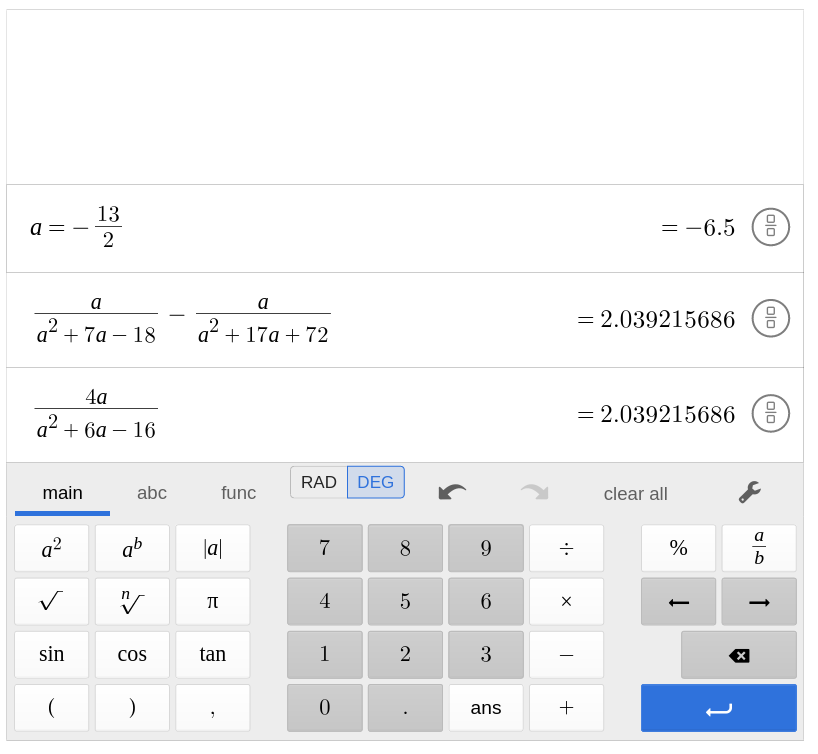
Clearly, $a=0$ is a solution. Using desmos, we may check the other solution,
$\displaystyle a=-\frac{13}{2}:$

$\displaystyle \frac{ p+1}{ p }+\frac{ 10}{ p - 5 }=\frac{4 p - 5 }{ p^2 -5 p}$ (one bonafide, one extraneous)
$$
\begin{array}{lll}
&\displaystyle \frac{ p+1}{ p }+\frac{ 10}{ p - 5 }=\frac{4 p - 5 }{ p^2 -5 p}&\mbox{}\\
\implies &\displaystyle \frac{ p+1}{ p }+\frac{ 10}{ p - 5 }=\frac{4 p - 5 }{ p(p -5) }&\mbox{factor all denominators}\\
\implies &\displaystyle \color{magenta}{p(p-5)}\frac{ p+1}{ p }+\color{magenta}{p(p-5)}\frac{ 10}{ p - 5 }=\color{magenta}{p(p-5)}\frac{4 p - 5 }{ p(p -5) }&\mbox{multiply by special factor}\\
\implies &\displaystyle \color{magenta}{(p-5)}(p+1)+\color{magenta}{p}\cdot 10=4 p - 5 &\mbox{cancel common factors}\\
\implies &\displaystyle p^2+p-5p-5+10p=4p-5 &\mbox{}\\
\implies &\displaystyle p^2+6p-5=4p-5 &\mbox{}\\
\implies &\displaystyle p^2+6p=4p&\mbox{}\\
\implies &\displaystyle p^2+6p\color{magenta}{-4p}=4p\color{magenta}{-4p}&\mbox{}\\
\implies &\displaystyle p^2+2p=0&\mbox{}\\
\implies &\displaystyle p(p+2)=0&\mbox{factor}\\
\implies &\displaystyle p=0 \,\,\,\,\mbox{or}\,\,\,\,p+2=0&\mbox{zero factor property}\\
\implies &\displaystyle p=0 \,\,\,\,\mbox{or}\,\,\,\,p=-2&\mbox{}\\
\end{array}
$$
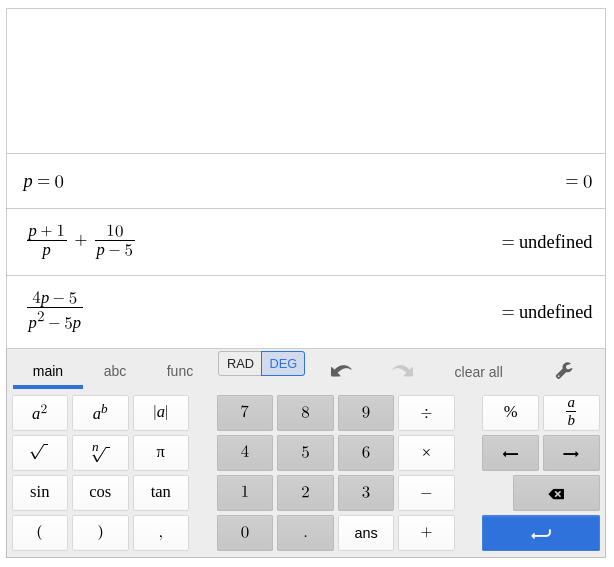
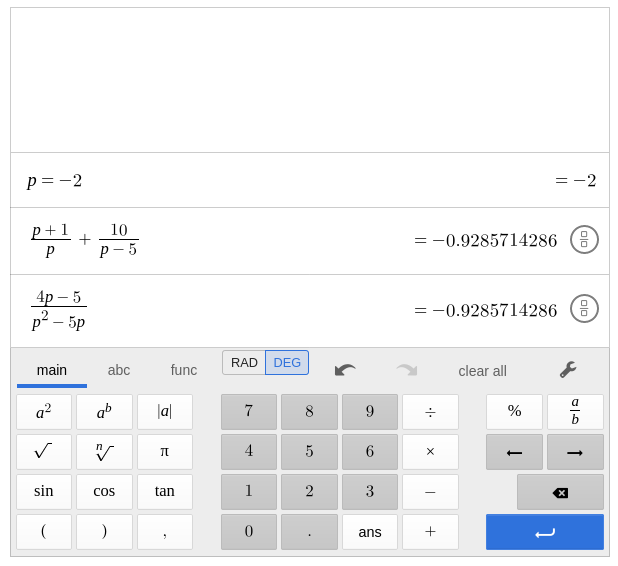
Checking our work, we see that $0$ cannot truly be a solution, so we must discard it.
Therefore, the only solution is $p=-2.$
Checking our work with desmos:
Therefore, the only solution is $p=-2.$
Checking our work with desmos:


$\displaystyle \frac{ s+1}{ s }+\displaystyle \frac{ 4}{ s - 2 }=\displaystyle \frac{5 s - 2 }{ s^2 -2 s}$ (two extraneous)
$$
\begin{array}{lll}
&\displaystyle \frac{ s+1}{ s }+\frac{ 4}{ s - 2 }= \frac{5 s - 2 }{ s^2 -2 s}&\mbox{}\\
\implies &\displaystyle \frac{ s+1}{ s }+\frac{ 4}{ s - 2 }= \frac{5 s - 2 }{ s(s -2)}&\mbox{factor all denominators}\\
\implies &\displaystyle \frac{ s+1}{ s }\color{magenta}{s(s-2)}+\frac{ 4}{ s - 2 }\color{magenta}{s(s-2)}= \frac{5 s - 2 }{ s(s -2)}\color{magenta}{s(s-2)}&\mbox{multiply by special factor}\\
\implies &\displaystyle (s+1)\color{magenta}{(s-2)}+4\color{magenta}{s}= 5 s - 2 &\mbox{cancel common factors}\\
\implies &\displaystyle s^2-s-2+4s=5s-2 &\mbox{FOIL and simplify}\\
\implies &\displaystyle s^2+3s-2=5s-2 &\mbox{simplify}\\
\implies &\displaystyle s^2+3s-2\color{magenta}{-5s}\color{blue}{+2}=5s+2\color{magenta}{-5s}\color{blue}{+2}&\mbox{subtract $5s$ and and add 2 on both sides}\\
\implies &\displaystyle s^2-2s=0&\mbox{simplify}\\
\implies &\displaystyle s(s-2)=0&\mbox{factor}\\
\implies &\displaystyle s=0 \,\,\,\,\mbox{or}\,\,\,\,s-2=0&\mbox{zero factor property}\\
\implies &\displaystyle s=0 \,\,\,\,\mbox{or}\,\,\,\,s=2&\mbox{}\\
\end{array}
$$
Since both solutions, $s=0$ and $s=2,$ result in zero denominators, this equation has no solution.
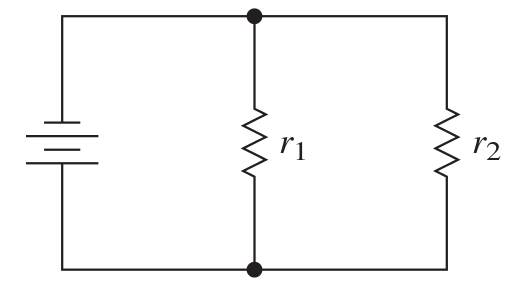
Application: Electrical Resistance
The total resistance $R$ in a parallel circuit with two individual resistors $r_1$ and $r_2$ can be calculated by using the formula $\displaystyle \frac{1}{R}=\displaystyle \frac{1}{r_1}+\displaystyle \frac{1}{r_2}.$ The resistance planned by an electrical technician for a parallel electric circuit with two resistors is $41.2$ $\Omega$. The resistance of $r_2$ must be $6$ times the resistance of $r_1.$ Determine the resistance of each resistor. Round your answer to the nearest hundredth of an ohm.
$$
\begin{array}{|lc|}\hline
{\bf \mbox{English Statement}} & {\bf \mbox{Mathematical Statement}}\\\hline
\mbox{Total resistance is } 41.2\Omega & R=41.2\\\hline
\mbox{Resistance of $r_2$ is $6$ times resistance $r_1$ } & r_2=6r_1\\\hline
\end{array}
$$
Using the above, we may say the following:
$$
\begin{array}{lll}
&\displaystyle \frac{1}{R}=\displaystyle \frac{1}{r_1}+\displaystyle \frac{1}{r_2}&\mbox{}\\
\implies &\displaystyle \frac{1}{\color{blue}{41.2}}=\displaystyle \frac{1}{r_1}+\displaystyle \frac{1}{\color{blue}{6r_1}}&\mbox{using} \color{blue}{\mbox{ known information}}\\
\implies &\displaystyle \color{magenta}{41.2\cdot 6 \cdot r_1 }\frac{1}{41.2}=\color{magenta}{41.2\cdot 6 \cdot r_1 }\frac{1}{r_1}+\color{magenta}{41.2\cdot 6 \cdot r_1 }\frac{1}{6r_1}&\mbox{multiply by something which cancels all denoms}\\
\implies &\displaystyle \color{magenta}{6 \cdot r_1 }=\color{magenta}{41.2\cdot 6 }+\color{magenta}{41.2}&\mbox{cancel}\\
\implies &\displaystyle 6 r_1 =288.4&\mbox{simplify}\\
\implies &\displaystyle \frac{6 r_1}{\color{magenta}{6}} =\frac{288.4}{\color{magenta}{6}}&\mbox{divide both sides by 6}\\
\implies &\displaystyle r_1 \approx 48.07 &\mbox {simplify}\\
\end{array}
$$
The resistance of of the first resistor is approximately $48.07$ ohms, and the second resistor is $6 r_1 =288.4$ ohms.