Arithmetic of Rational Expressions: Rational expressions have their own arithmetic (addition, subtraction, multiplication, and division).
We've added, subtracted, multiplied, and divided rational expressions. Now we're going apply multiple operations at the same time.
Mixing it Up: To perform multiple operations on rational expressions, use the order of operations.
Example: Simplify the following rational expression.
$\displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\displaystyle \frac{ 3 r - 5 }{ 4 r ^2 + 3 r - 10 } \div \displaystyle \frac{ 5 - 3 r } {r + 2 }$
$$
\begin{array}{cll}
\displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\frac{ 3 r - 5 }{ 4 r ^2 + 3 r - 10 }\div \frac{ 5 - 3 r } {r + 2 } &= \displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\frac{ 3 r - 5 }{ 4 r ^2 + 3 r - 10 }\cdot \frac{r + 2 }{ 5 - 3 r } &\mbox{invert and multiply}\\
&= \displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\frac{ \color{magenta}{(3 r - 5)}\cdot 1 }{ (4r-5)\color{magenta}{(r+2)} }\cdot \frac{\color{magenta}{(r + 2)}\cdot 1 }{-1\cdot\color{magenta}{(3r-5)}} &\mbox{factor like crazy}\\
&= \displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\frac{ 1 }{ 4r-5 }\cdot \frac{ 1 }{-1} &\mbox{cancel common factors}\\
&= \displaystyle \frac{ 6 r - 6 }{ 4 r - 5}+\frac{ 1 }{ 4r-5 } &\mbox{simplify}\\
&= \displaystyle \frac{ 6 r - 6 + 1 }{ 4r-5 } &\mbox{add over common denom}\\
&= \displaystyle \frac{ 6 r - 5 }{ 4r-5 } &\mbox{simplify}\\
\end{array}
$$
Complex Fractions
A complex fraction is a fraction whose numerator and denominator are...
You guessed it!
Fractions!
Example: $\displaystyle \frac{ \displaystyle \frac{k^2-8k+15}{k^2-10k+25} }{ \displaystyle \frac{k^2-6k+9}{11 k^2-275} }$
$$
\begin{array}{cll}
\displaystyle \frac{ \displaystyle \frac{k^2-8k+15}{k^2-10k+25} }{ \displaystyle \frac{k^2-6k+9}{11 k^2-275} } &= \displaystyle \displaystyle \frac{k^2-8k+15}{k^2-10k+25} \div \displaystyle \frac{k^2-6k+9}{11 k^2-275} &\mbox{turn into division problem}\\
&= \displaystyle \frac{k^2-8k+15}{k^2-10k+25} \cdot \displaystyle \frac{11 k^2-275}{k^2-6k+9} &\mbox{invert and multiply}\\
&= \displaystyle \frac{(k-3)(k-5)}{(k-5)(k-5)} \cdot \displaystyle \frac{11(k^2-25)}{(k-3)(k-3)} &\mbox{factor like crazy}\\
&= \displaystyle \frac{\color{magenta}{(k-3)(k-5)}}{\color{magenta}{(k-5)(k-5)}} \cdot \displaystyle \frac{11(k+5)\color{magenta}{(k-5)}}{\color{magenta}{(k-3)}(k-3)} &\mbox{identify } \color{magenta}{\mbox{common}} \mbox{ factors}\\
&= \displaystyle \displaystyle \frac{11(k+5)}{k-3} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}\\
\end{array}
$$
How Handle Complex Fractions
Method: Use the tried and true "invert and multiply."
$\displaystyle \frac{ \displaystyle \frac{k^2-8k+15}{k^2-10k+25} }{ \displaystyle \frac{k^2-6k+9}{11 k^2-275} }$
We did this one already!
$\displaystyle \frac{ 6 r - 6 }{ 4 r - 5}-\displaystyle \frac{\displaystyle \frac{ 3 r - 5 }{ 4 r ^2 + 3 r - 10 }}{\displaystyle \frac{ 5 - 3 r } {r + 2 }}$ (this example should look familiar)
We did this one already!
How Handle Complex Fractions: Get into "fraction over a fraction" form.
$\displaystyle \frac{ \displaystyle \frac{1}{n t^2}+\displaystyle \frac{1}{n^2t} }{ \displaystyle \frac{1}{t}+\displaystyle \frac{1}{n} }$
$$
\begin{array}{cll}
\displaystyle \frac{ \displaystyle \frac{1}{n t^2}+\displaystyle \frac{1}{n^2t} }{ \displaystyle \frac{1}{t}+\displaystyle \frac{1}{n} } &= \displaystyle \frac{ \displaystyle \frac{\color{\magenta}{n}}{\color{\magenta}{n}\cdot n t^2}+\displaystyle \frac{\color{\magenta}{t}}{n^2t\cdot \color{\magenta}{t}} }{ \displaystyle \frac{\color{\magenta}{n}}{\color{\magenta}{n}t}+\displaystyle \frac{\color{\magenta}{t}}{\color{\magenta}{t}n} } &\mbox{get common denom in top and bottom}\\
&= \displaystyle \frac{ \displaystyle \frac{n+t}{n^2 t^2} }{ \displaystyle \frac{n+t}{nt}} &\mbox{now in fraction-over-fraction form}\\
&= \displaystyle \displaystyle \frac{n+t}{n^2 t^2}\div \displaystyle \frac{n+t}{nt} &\mbox{express as division}\\
&= \displaystyle \displaystyle \frac{n+t}{n^2 t^2}\cdot \displaystyle \frac{nt}{n+t} &\mbox{invert and multiply}\\
&= \displaystyle \frac{\color{magenta}{(n+t)}\cdot \color{magenta}{n}\cdot \color{magenta}{t} }{\color{magenta}{n}\cdot n \cdot \color{magenta}{t} \cdot t \cdot \color{magenta}{(n+t)}} &\mbox{factor like crazy, identify} \color{magenta}{\mbox{ common }} \mbox{factors}\\
&= \displaystyle \frac{ \displaystyle 1 }{ \displaystyle nt } &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}\\
\end{array}
$$
$\displaystyle \frac{ v-\displaystyle \frac{1}{x} }{ x-\displaystyle \frac{1}{v} }$
$$
\begin{array}{cll}
\displaystyle \frac{ v-\displaystyle \frac{1}{x} }{ x-\displaystyle \frac{1}{v} } &= \displaystyle \frac{ \displaystyle \frac{v}{1}-\frac{1}{x} }{\displaystyle \frac{x}{1}- \frac{1}{v} } &\mbox{make everything into fractions}\\
&= \displaystyle \frac{\displaystyle \frac{v\cdot \color{magenta}{x}}{1\cdot \color{magenta}{x}}- \frac{1}{x} }{\displaystyle \frac{x\cdot \color{magenta}{v}}{1\cdot \color{magenta}{v}}- \frac{1}{v} } &\mbox{get common denom}\\
&= \displaystyle \frac{\displaystyle \frac{xv}{x}- \frac{1}{x} }{\displaystyle \frac{xv}{v}- \frac{1}{v} } &\mbox{simplify}\\
&= \displaystyle \frac{\displaystyle \frac{xv-1}{x}}{\displaystyle \frac{xv-1}{v}} &\mbox{now in fraction-over-fraction form}\\
&= \displaystyle \displaystyle \frac{xv-1}{x}\div \displaystyle \frac{xv-1}{v} &\mbox{express as division}\\
&= \displaystyle \displaystyle \frac{\color{magenta}{xv-1}}{x}\cdot \displaystyle \frac{v}{\color{magenta}{xv-1}} &\mbox{invert and multiply, } \mbox{identify } \color{magenta}{\mbox{common}} \mbox{ factors}\\
&= \displaystyle \frac{ \displaystyle v }{ \displaystyle x } &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}\\
\end{array}
$$
Remember: Fraction-Over-Fraction Form
$$\displaystyle \frac{ \displaystyle \frac{1+\displaystyle \frac{p}{x}}{1-\displaystyle \frac{p}{x}} }{ \displaystyle \frac{p+x}{p-\displaystyle \frac{x^2}{p}} }$$
$$
\begin{array}{cll}
\displaystyle \frac{ \displaystyle \frac{1+\displaystyle \frac{p}{x}}{1-\displaystyle \frac{p}{x}} }{ \displaystyle \frac{p+x}{p-\displaystyle \frac{x^2}{p}} } &= \displaystyle \frac{1+\displaystyle \frac{p}{x}}{1-\displaystyle \frac{p}{x}} \div \displaystyle \frac{p+x}{p-\displaystyle \frac{x^2}{p}} &\mbox{re-express as division problem}\\
&= \displaystyle \frac{x+p}{x-p} \div \displaystyle \frac{p}{p-x} &\mbox{after side calc}\\
&= \displaystyle \frac{x+p}{\color{magenta}{x-p}} \cdot \frac{\color{magenta}{p-x}}{p} &\mbox{invert and multiply, }\mbox{identify } \color{magenta}{\mbox{common}} \mbox{ factors}\\
&= \displaystyle \frac{x+p}{-1} \cdot \frac{1}{p} &\mbox{cancel to $-1$}\\
&= \displaystyle -\frac{x+p}{p} &\mbox{simplify}\\
\end{array}
$$
Application of Complex Fractions
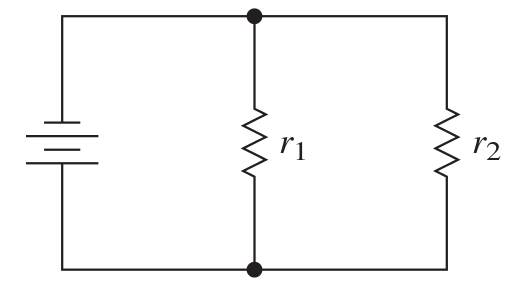
Electrical Resistance: The total resistance $R$ in a parallel circuit with two individual resistors $r_1$ and $r_2$ can be calculated by using the formula $$R=\displaystyle \frac{1}{\displaystyle \frac{1}{r_1}+\displaystyle \frac{1}{r_2}}.$$
$$
\begin{array}{cll}
\displaystyle R &= \displaystyle \frac{1}{\displaystyle \frac{1}{r_1}+\displaystyle \frac{1}{r_2}} &\mbox{state general formula}\\
&= \displaystyle \frac{1}{\displaystyle \frac{1}{41}+\displaystyle \frac{1}{8}} &\mbox{substitute in known values}\\
&= \displaystyle \frac{1}{\displaystyle \frac{1}{41}\cdot\color{magenta}{\frac{8}{8}}+\displaystyle \frac{1}{8}\cdot\color{magenta}{\frac{41}{41}}} &\mbox{multiply by fancy ones}\\
&= \displaystyle \frac{1}{\displaystyle \frac{8}{328}+\displaystyle \frac{41}{328}} &\mbox{get common denom}\\
&= \displaystyle \frac{1}{\displaystyle \frac{8+41}{328}} &\mbox{add over common denom}\\
&= \displaystyle \frac{1}{\displaystyle \frac{49}{328}} &\mbox{simplify}\\
&= \displaystyle 1\div \frac{49}{328} &\mbox{re-express as division problem}\\
&= \displaystyle 1 \cdot \frac{328}{49} &\mbox{invert and multiply}\\
&= \displaystyle \frac{328}{49} &\mbox{}\\
&\approx\displaystyle 6.69 &\mbox{approximate as a decimal}\\
\end{array}
$$
The total resistance of the circuit is about $6.69$ ohms.