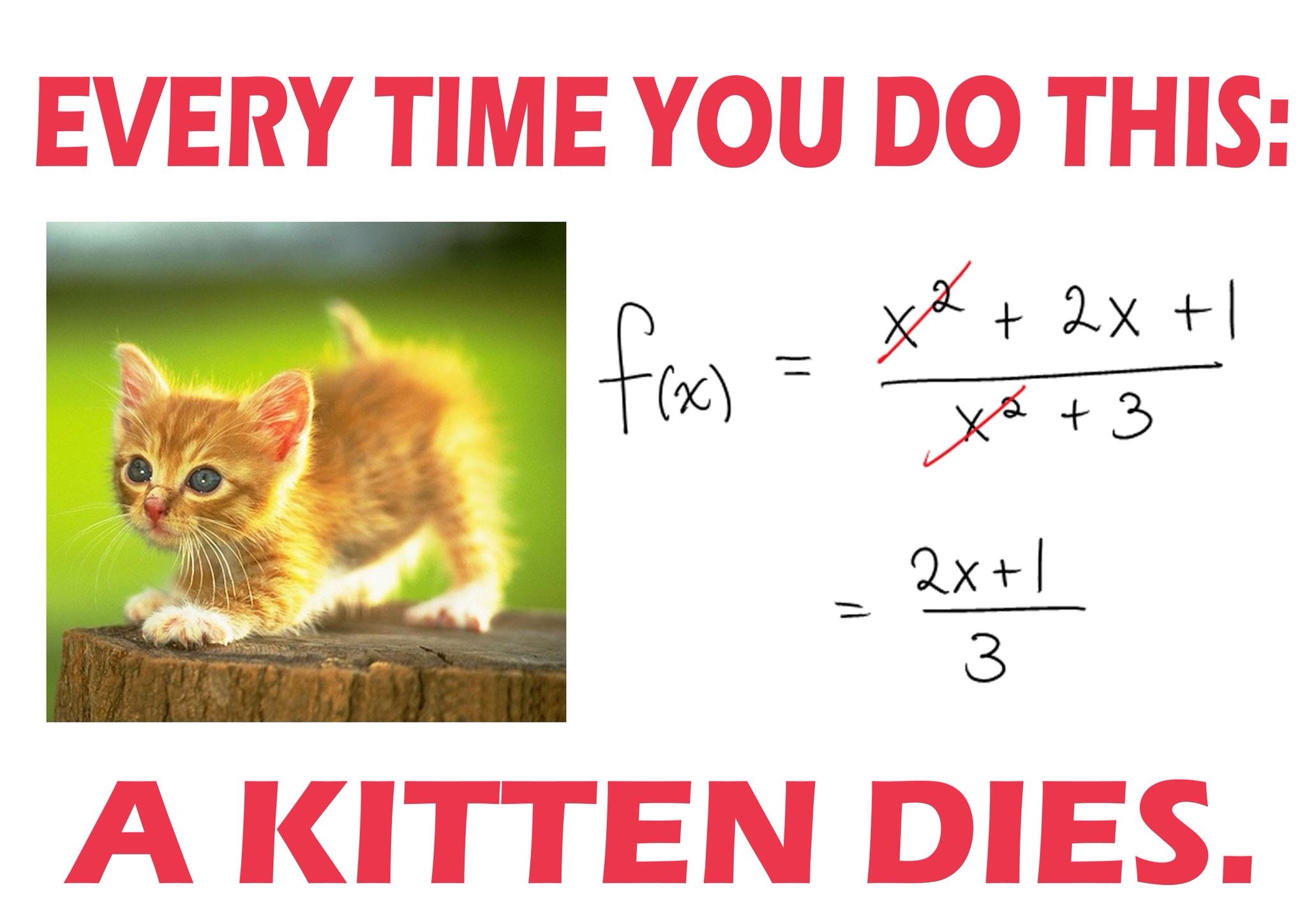Definition: a rational expression is a quotient of two polynomial expressions.
Examples:
$\displaystyle \frac{3x^2-2x+5}{x-2}$
$\displaystyle \frac{2x+5}{-2x^3-2x^2+5}$
$\displaystyle \frac{x^2-2x+5}{1}=x^2-2x+5$ (i.e., all polynomial expressions are also rational expressions.)
Where Rational Expressions are Undefined
Any real number which makes the denominator $0$ makes the rational expression undefined.
Example: The value of $x=2$ makes the rational expression $\displaystyle \frac{1}{x-2}$ undefined.
More Examples
Example: Determine the value(s) for which the rational expression $\displaystyle\frac{1}{x^2-x-6}$ is undefined.
The denominator is $0$ when $x^2-x-6=(x-3)(x+2)=0.$ ,
So, the rational expression is undefined when $x=3$ and $x=-2.$
So, the rational expression is undefined when $x=3$ and $x=-2.$
Example: Determine the value(s) for which the rational expression $\displaystyle\frac{2x}{2x-7}$ is undefined.
The denominator is $0$ when $2x-7=0.$
So, the rational expression is undefined when $\displaystyle x=\frac{7}{2}.$
So, the rational expression is undefined when $\displaystyle x=\frac{7}{2}.$
Example: Determine the value(s) for which the rational expression $\displaystyle\frac{2 x^2+5 x-42}{12 x^2+15 x+3}$ is undefined.
The denominator is $0$ when $12 x^2+15 x+3=3(4x^2+5x+1)=3(4x+1)(x+1)=0.$
So, the rational expression is undefined when $x=\displaystyle -\frac{1}{4}$ and $x=-1.$
So, the rational expression is undefined when $x=\displaystyle -\frac{1}{4}$ and $x=-1.$
Simplifying Rational Expressions
Fact: Like regular fractions, we can reduce rational expressions.
Examples: Reduce the following rational expressions.
$\displaystyle \frac{x+1}{(x-2)(x+1)}$
$\displaystyle \frac{(2t+5)(3t+1)}{2t+5}$
$\displaystyle \frac{b^2+5b+6}{b^2-b-6}$
$$
\begin{array}{cll}
\displaystyle \frac{b^2+5b+6}{b^2-b-6} &= \displaystyle \frac{(b+3)\color{magenta}{(b+2)}}{(b-3)\color{magenta}{(b+2)}} &\mbox{factor numerator and denominator}\\
&= \displaystyle \frac{b+3}{b-3} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}
\end{array}
$$
Reducing Rational Expressions
Process: To reduce (simplify) a rational expression:
$1)$ Completely factor the numerator and denominator
$2)$ Cancel any common factors
Reducing Rational Expressions: More Examples
$\displaystyle \frac{ 3 m^2-19 m+20}{m^2-5m}$
$$
\begin{array}{cll}
\displaystyle \frac{ 3 m^2-19 m+20}{m^2-5m} &= \displaystyle \frac{(3m-4)\color{magenta}{(m-5)}}{m\color{magenta}{(m-5)}} &\mbox{factor numerator and denominator}\\
&= \displaystyle \frac{3m-4}{m} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}
\end{array}
$$
$\displaystyle \frac{ 49 a^2-49 }{14 + 14 a}$
$$
\begin{array}{cll}
\displaystyle \frac{ 49 a^2-49 }{14 + 14 a} &= \displaystyle \frac{7\cdot 7 \cdot (a-1)(a+1)}{2\cdot 7 (1+a)} &\mbox{factor numerator and denominator}\\
&= \displaystyle \frac{7\cdot (a-1)\color{magenta}{\cdot 7\cdot (a+1)}}{2\cdot \color{magenta}{ 7\cdot (1+a)}} &\mbox{recognize } \color{magenta}{\mbox{common}} \mbox{ factors}\\
&= \displaystyle \frac{7(a-1)}{2} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}\\
&= \displaystyle \frac{7a-7}{2} &\mbox{simplify if necessary}\\
\end{array}
$$
$\displaystyle \frac{ 4 z^2-37 z+40}{3 z-24}$
$$
\begin{array}{cll}
\displaystyle \frac{ 4 z^2-37 z+40}{3 z-24} &= \displaystyle \frac{(4z-5)\color{magenta}{(z-8)}}{3\color{magenta}{(z-8)}} &\mbox{factor numerator and denominator}\\
&= \displaystyle \frac{4z-5}{3} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}
\end{array}
$$
$\displaystyle \frac{ 3 u^2-10 u t + 8 t^2}{ 3 u^2-u t -4 t^2}$
$$
\begin{array}{cll}
\displaystyle \frac{ 3 u^2-10 u t + 8 t^2}{ 3 u^2-u t -4 t^2} &= \displaystyle \frac{(u-2t)\color{magenta}{(3u-4t)}}{(u+t)\color{magenta}{(3u-4t)}} &\mbox{factor numerator and denominator}\\
&= \displaystyle\frac{u-2t}{u+t} &\mbox{cancel } \color{magenta}{\mbox{common}} \mbox{ factors}
\end{array}
$$
One More Important Example: Reduce the rational expression. $$\displaystyle \frac{x^2+2x+1}{x^2+3}$$ Indeed. Some things are oh so very tempting.
But PLEASE remember...