We now reap one of the many rewards of power series by solving linear ODEs in a very efficient way.
The Big Idea
To solve the equation $$ p(x)y''+q(x)y'+r(x)y=0 $$ we assume a series solution $$y=\displaystyle \sum_{k=0}^{\infty}a_k (x-x_0)^k$$ where $x_0$ is suitably chosen.
We often choose $x_0=0$ since the series representation is easier and since initial conditions often begin at time equal $0.$
Example
Solve the equation $y'-2xy=0$ using a power series at $x_0=0.$
To solve this equation, we will express out unknown solution as an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k.$
Then,
$$
\begin{array}{lll}
&\displaystyle y'-2xy=1 &\mbox{}\\
\implies &\displaystyle \left(\sum_{k=0}^{\infty}a_k x^k\right)'-2x\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=1}^{\infty}a_k k x^{k-1}-2x\sum_{k=0}^{\infty}a_k x^k=0&\mbox{differentiating term by term}\\
\implies &\displaystyle a_1+\sum_{k=2}^{\infty}a_k k x^{k-1}-\sum_{k=0}^{\infty}2 a_k x^{k+1}=0&\mbox{peeling off the first term of the first series}\\
\implies &\displaystyle a_1+\sum_{k=1}^{\infty}a_{k+1} (k+1) x^{k}-\sum_{k=1}^{\infty}2 a_{k-1} x^{k}=0&\mbox{re-indexing both sums}\\
\implies &\displaystyle a_1+\sum_{k=1}^{\infty}\left[a_{k+1} (k+1) x^{k}-2 a_{k-1}\right] x^{k}=0&\mbox{using properties of series}\\
\end{array}
$$
The only way the above series can be identically zero for all $x$ is if $a_1=0$ and $(k+1)a_{k+1}-2 a_{k-1}=0$ for all $k \geq 1.$
From these equations, we may determine the coefficients $a_1, a_2, a_3, \ldots$
From the first equation, we know that $a_1=0.$
For the second equation which is a recurrence relation, we rewrite it as $ka_{k} -2 a_{k-2}=0$ for all $k\geq 2,$ which more conveniently becomes $$ a_{k} =\frac{2}{k}a_{k-2} \mbox{ for all } k\geq 2 $$ Then, $$ \begin{array}{lll} \displaystyle a_0 & &\mbox{an unknown constant}\\ a_1 &=\displaystyle 0&\mbox{}\\ a_2 &=\displaystyle \frac{2}{2}a_{0}=a_0&\mbox{}\\ a_3 &=\displaystyle \frac{2}{3}\cdot 0=0&\mbox{}\\ a_4 &=\displaystyle \frac{2}{4} a_{2}=\frac{1}{2}a_2=\frac{1}{2}a_0&\mbox{}\\ a_5 &=\displaystyle \frac{2}{5} a_{3}=0&\mbox{}\\ a_6 &=\displaystyle \frac{2}{6} a_{4}=\frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_7 &=\displaystyle \frac{2}{7} a_{5}=0&\mbox{}\\ a_8 &=\displaystyle \frac{2}{8} a_{6}=\frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_9 &=\displaystyle \frac{2}{9} a_{7}=0&\mbox{}\\ a_{10} &=\displaystyle \frac{2}{10} a_{8}=\frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ &\vdots& \end{array} $$ From the above we can see the pattern: $$ a_{2k+1}= 0 $$ and $$ a_{2k}=\frac{1}{k}\cdots \frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0=\frac{1}{k!}a_0 $$ Our solution is then $$ \begin{array}{ll} y&=\displaystyle \sum_{k=0}^{\infty}a_k x^k\\ &=\displaystyle \sum_{k=0}^{\infty}a_{2k}x^{2k}+\sum_{k=0}^{\infty}a_{2k+1}x^{2k+1}\\ &=\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!}a_0 x^{2k}+\sum_{k=0}^{\infty}0\cdot x^{2k+1}\\ &=\displaystyle a_0\sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}\\ \end{array} $$ We note that $a_0$ is the constant of our general solution. We also recognize the series $\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}$ as none other than $e^{x^2}.$ Thus, $$ y=a_0e^{x^2} $$
From these equations, we may determine the coefficients $a_1, a_2, a_3, \ldots$
From the first equation, we know that $a_1=0.$
For the second equation which is a recurrence relation, we rewrite it as $ka_{k} -2 a_{k-2}=0$ for all $k\geq 2,$ which more conveniently becomes $$ a_{k} =\frac{2}{k}a_{k-2} \mbox{ for all } k\geq 2 $$ Then, $$ \begin{array}{lll} \displaystyle a_0 & &\mbox{an unknown constant}\\ a_1 &=\displaystyle 0&\mbox{}\\ a_2 &=\displaystyle \frac{2}{2}a_{0}=a_0&\mbox{}\\ a_3 &=\displaystyle \frac{2}{3}\cdot 0=0&\mbox{}\\ a_4 &=\displaystyle \frac{2}{4} a_{2}=\frac{1}{2}a_2=\frac{1}{2}a_0&\mbox{}\\ a_5 &=\displaystyle \frac{2}{5} a_{3}=0&\mbox{}\\ a_6 &=\displaystyle \frac{2}{6} a_{4}=\frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_7 &=\displaystyle \frac{2}{7} a_{5}=0&\mbox{}\\ a_8 &=\displaystyle \frac{2}{8} a_{6}=\frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_9 &=\displaystyle \frac{2}{9} a_{7}=0&\mbox{}\\ a_{10} &=\displaystyle \frac{2}{10} a_{8}=\frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ &\vdots& \end{array} $$ From the above we can see the pattern: $$ a_{2k+1}= 0 $$ and $$ a_{2k}=\frac{1}{k}\cdots \frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0=\frac{1}{k!}a_0 $$ Our solution is then $$ \begin{array}{ll} y&=\displaystyle \sum_{k=0}^{\infty}a_k x^k\\ &=\displaystyle \sum_{k=0}^{\infty}a_{2k}x^{2k}+\sum_{k=0}^{\infty}a_{2k+1}x^{2k+1}\\ &=\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!}a_0 x^{2k}+\sum_{k=0}^{\infty}0\cdot x^{2k+1}\\ &=\displaystyle a_0\sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}\\ \end{array} $$ We note that $a_0$ is the constant of our general solution. We also recognize the series $\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}$ as none other than $e^{x^2}.$ Thus, $$ y=a_0e^{x^2} $$
Yeah, but couldn't we have just solved that equation using first-order methods?
Example
Find the first $6$ non-zero terms of the power series solution to Airy's equation $y''-xy=0$ centered at $x_0=0.$
We will express out unknown solution as an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k.$
Then,
$$
\begin{array}{lll}
&\displaystyle y''-xy=0 &\mbox{}\\
\implies &\displaystyle \left(\sum_{k=0}^{\infty}a_k x^k\right)''-x\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}a_k k(k-1)x^{k-2}-\sum_{k=0}^{\infty}a_k x^{k+1}=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}-\sum_{k=1}^{\infty}a_{k-1} x^{k}=0&\mbox{re-index sums for common power}\\
\implies &\displaystyle 2a_2+\sum_{k=1}^{\infty}a_{k+2} (k+2)(k+1)x^{k}-\sum_{k=1}^{\infty}a_{k-1} x^{k}=0&\mbox{peel off extra term in first sum}\\
\implies &\displaystyle 2a_2+\sum_{k=1}^{\infty}\left[a_{k+2} (k+2)(k+1)-a_{k-1}\right]x^{k}=0&\mbox{}\\
\end{array}
$$
For the above to be identically $0,$ is must be that $a_2=0$ and $a_{k+2} (k+2)(k+1)-a_{k-1}=0$ for all $k\geq 1.$
Then, $$ a_{k+2}=\frac{1}{(k+2)(k+1)}a_{k-1} $$ which becomes $$ a_{k+3}=\frac{1}{(k+3)(k+2)}a_{k} $$ for $k\geq 0.$
We now determine our coefficients noting that $a_0$ and $a_1$ are an undermined constants. $$ \begin{array}{lll} \displaystyle a_0&=\displaystyle a_0 & \mbox{}\\ \displaystyle a_1&=\displaystyle a_1 & \mbox{}\\ \displaystyle a_2&=\displaystyle 0 & \mbox{as explained above}\\ \displaystyle a_3&=\displaystyle \frac{1}{3\cdot 2}a_{0}=\frac{1}{6}a_0 & \mbox{}\\ \displaystyle a_4&=\displaystyle \frac{1}{4\cdot 3}a_{1}=\frac{1}{12}a_1 & \mbox{}\\ \displaystyle a_5&=\displaystyle \frac{1}{5\cdot 4}a_{2}=0 & \mbox{}\\ \displaystyle a_6&=\displaystyle \frac{1}{6\cdot 5}a_{3}=\frac{1}{6\cdot 5}\cdot\frac{1}{6}a_{0}=\frac{1}{180}a_0 & \mbox{}\\ \displaystyle a_7&=\displaystyle \frac{1}{7\cdot 6}a_{4}=\frac{1}{7\cdot 6}\cdot\frac{1}{12}a_1=\frac{1}{504}a_1 & \mbox{}\\ \displaystyle a_8&=\displaystyle \frac{1}{8\cdot 7}a_{5}=0 & \mbox{}\\ \vdots&&\\ \end{array} $$ We write our general solution as $$ \begin{array}{lll} \displaystyle y&\displaystyle=\sum_{k=0}^{\infty}a_k x^k &\mbox{}\\ &\displaystyle= a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+a_5 x^5+a_6 x^6+a_7 x^7+a_8 x^8+\cdots &\mbox{}\\ &\displaystyle= a_0+a_1 x+0\cdot x^2+\frac{1}{6}a_0 x^3+\frac{1}{12}a_1 x^4+0\cdot x^5+\frac{1}{180}a_0 x^6+\frac{1}{504}a_1 x^7+0\cdot x^8+\cdots &\mbox{}\\ &\displaystyle= a_0+a_1 x+\frac{1}{6}a_0 x^3+\frac{1}{12}a_1 x^4+\frac{1}{180}a_0 x^6+\frac{1}{504}a_1 x^7+\cdots &\mbox{}\\ &\displaystyle= a_0+\frac{1}{6}a_0 x^3+\frac{1}{180}a_0 x^6+\cdots+a_1 x+\frac{1}{12}a_1 x^4+\frac{1}{504}a_1 x^7+0\cdot x^8+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0\left(1+\frac{1}{6}x^3+\frac{1}{180}x^6+\cdots\right)+a_1\left(x+\frac{1}{12}x^4+\frac{1}{504}x^7+\cdots\right) &\mbox{}\\ \end{array} $$
Then, $$ a_{k+2}=\frac{1}{(k+2)(k+1)}a_{k-1} $$ which becomes $$ a_{k+3}=\frac{1}{(k+3)(k+2)}a_{k} $$ for $k\geq 0.$
We now determine our coefficients noting that $a_0$ and $a_1$ are an undermined constants. $$ \begin{array}{lll} \displaystyle a_0&=\displaystyle a_0 & \mbox{}\\ \displaystyle a_1&=\displaystyle a_1 & \mbox{}\\ \displaystyle a_2&=\displaystyle 0 & \mbox{as explained above}\\ \displaystyle a_3&=\displaystyle \frac{1}{3\cdot 2}a_{0}=\frac{1}{6}a_0 & \mbox{}\\ \displaystyle a_4&=\displaystyle \frac{1}{4\cdot 3}a_{1}=\frac{1}{12}a_1 & \mbox{}\\ \displaystyle a_5&=\displaystyle \frac{1}{5\cdot 4}a_{2}=0 & \mbox{}\\ \displaystyle a_6&=\displaystyle \frac{1}{6\cdot 5}a_{3}=\frac{1}{6\cdot 5}\cdot\frac{1}{6}a_{0}=\frac{1}{180}a_0 & \mbox{}\\ \displaystyle a_7&=\displaystyle \frac{1}{7\cdot 6}a_{4}=\frac{1}{7\cdot 6}\cdot\frac{1}{12}a_1=\frac{1}{504}a_1 & \mbox{}\\ \displaystyle a_8&=\displaystyle \frac{1}{8\cdot 7}a_{5}=0 & \mbox{}\\ \vdots&&\\ \end{array} $$ We write our general solution as $$ \begin{array}{lll} \displaystyle y&\displaystyle=\sum_{k=0}^{\infty}a_k x^k &\mbox{}\\ &\displaystyle= a_0+a_1 x+a_2 x^2+a_3 x^3+a_4 x^4+a_5 x^5+a_6 x^6+a_7 x^7+a_8 x^8+\cdots &\mbox{}\\ &\displaystyle= a_0+a_1 x+0\cdot x^2+\frac{1}{6}a_0 x^3+\frac{1}{12}a_1 x^4+0\cdot x^5+\frac{1}{180}a_0 x^6+\frac{1}{504}a_1 x^7+0\cdot x^8+\cdots &\mbox{}\\ &\displaystyle= a_0+a_1 x+\frac{1}{6}a_0 x^3+\frac{1}{12}a_1 x^4+\frac{1}{180}a_0 x^6+\frac{1}{504}a_1 x^7+\cdots &\mbox{}\\ &\displaystyle= a_0+\frac{1}{6}a_0 x^3+\frac{1}{180}a_0 x^6+\cdots+a_1 x+\frac{1}{12}a_1 x^4+\frac{1}{504}a_1 x^7+0\cdot x^8+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0\left(1+\frac{1}{6}x^3+\frac{1}{180}x^6+\cdots\right)+a_1\left(x+\frac{1}{12}x^4+\frac{1}{504}x^7+\cdots\right) &\mbox{}\\ \end{array} $$
A Few Notes on Airy's Equation
For $x \lt 0,$ the equation $y''-xy=0$ behaves sort of like $y''+y=0$ which has oscillatory behavior.
For $x \gt 0,$ the equation $y''-xy=0$ behaves sort of like $y''-y=0$ which grows exponentially.
The graph of the solutions $\color{darkblue}{y_1(x)=\displaystyle 1+\frac{1}{6}x^3+\frac{1}{180}x^6}+\cdots$ and $\displaystyle \color{darkgreen}{y_2(x)=x+\frac{1}{12}x^4+\frac{1}{504}x^7+\cdots}$ are shown below.
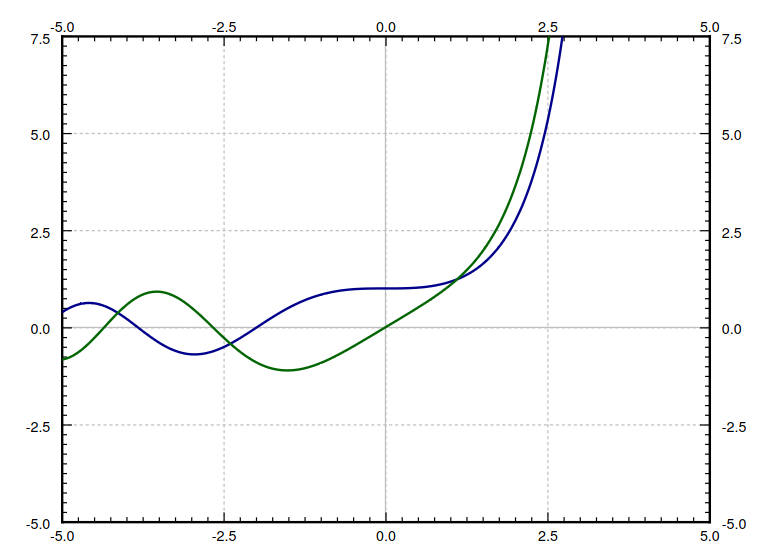
A Few Notes on Airy's Equation
According to Wikpedia article on Airy Functions,
"The Airy function is the solution to the time-independent Schrödinger equation for a particle confined within a triangular potential well and for a particle in a one-dimensional constant force field."
Example
Find the first $4$ nonzero terms of the power series solution of $$y''+(x-1)y'+y=0$$ centered at $x_0=0.$
We will express out unknown solution as an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k.$
Then,
$$
\begin{array}{lll}
&\displaystyle y''+(x-1)y'+y=0 &\mbox{}\\
\implies &\displaystyle \left(\sum_{k=0}^{\infty}a_k x^k\right)''+(x-1)\left(\sum_{k=0}^{\infty}a_k x^k\right)'+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}a_k k(k-1)x^{k-2}+(x-1)\sum_{k=1}^{\infty}a_k k x^{k-1}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\color{magenta}{(x-1)\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\color{magenta}{x\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}-\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k+1}-\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\color{blue}{\sum_{k=1}^{\infty} a_{k} k x^{k}}-\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\color{blue}{\sum_{k=0}^{\infty} a_{k} k x^{k}}-\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
%\implies &\displaystyle \sum_{k=0}^{\infty}a_{k+2} (k+2)(k+1)x^{k}+\sum_{k=0}^{\infty} a_{k} k x^{k}-\sum_{k=0}^{\infty} a_{k+1} (k+1) x^{k}+a_0+\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}\left[a_{k+2} (k+2)(k+1)+ a_{k} k - a_{k+1} (k+1) +a_k \right]x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}\left[a_{k+2} (k+2)(k+1)+ a_{k}(k+1) - a_{k+1} (k+1)\right]x^k=0&\mbox{}\\
\end{array}
$$
For the above to be identically $0$ for all $x,$ it must be that
$$
a_{k+2} (k+2)(k+1)x^{k}+ a_{k}(k+1) - a_{k+1} (k+1)=0
$$
that is,
$$
a_{k+2}=\frac{a_{k+1} (k+1)-a_{k} (k+1)}{(k+2)(k+1)}=\frac{a_{k+1}-a_k}{k+2}
$$
for all $k \geq 0.$
Treating $a_0$ and $a_1$ as undetermined constants, we may determine now determine $a_2$ and $a_3.$ $$ \begin{array}{lll} \displaystyle a_2&\displaystyle=\frac{a_1-a_0}{2}=\frac{1}{2}(a_1-a_0) &\mbox{}\\ \displaystyle a_3&\displaystyle=\frac{a_2-a_1}{3}=\frac{\frac{1}{2}(a_1-a_0)-a_1}{3}=\frac{-\frac{1}{2}a_1-\frac{1}{2}a_0}{3}=-\frac{1}{6}(a_1+a_0) &\mbox{}\\ \end{array} $$ So, $$ \begin{array}{lll} \displaystyle y&\displaystyle=\sum_{k=0}^{\infty}a_k x^k &\mbox{}\\ \displaystyle &\displaystyle=a_0+a_1x+a_2x^2+a_3x^3+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0+a_1x+\frac{1}{2}(a_1-a_0)x^2-\frac{1}{6}(a_1+a_0)x^3+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0\left(1-\frac{1}{2}x^2-\frac{1}{6}x^3+\cdots\right)+a_1\left(x+\frac{1}{2}x^2-\frac{1}{6}x^3+\cdots\right) &\mbox{}\\ \end{array} $$
Treating $a_0$ and $a_1$ as undetermined constants, we may determine now determine $a_2$ and $a_3.$ $$ \begin{array}{lll} \displaystyle a_2&\displaystyle=\frac{a_1-a_0}{2}=\frac{1}{2}(a_1-a_0) &\mbox{}\\ \displaystyle a_3&\displaystyle=\frac{a_2-a_1}{3}=\frac{\frac{1}{2}(a_1-a_0)-a_1}{3}=\frac{-\frac{1}{2}a_1-\frac{1}{2}a_0}{3}=-\frac{1}{6}(a_1+a_0) &\mbox{}\\ \end{array} $$ So, $$ \begin{array}{lll} \displaystyle y&\displaystyle=\sum_{k=0}^{\infty}a_k x^k &\mbox{}\\ \displaystyle &\displaystyle=a_0+a_1x+a_2x^2+a_3x^3+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0+a_1x+\frac{1}{2}(a_1-a_0)x^2-\frac{1}{6}(a_1+a_0)x^3+\cdots &\mbox{}\\ \displaystyle &\displaystyle=a_0\left(1-\frac{1}{2}x^2-\frac{1}{6}x^3+\cdots\right)+a_1\left(x+\frac{1}{2}x^2-\frac{1}{6}x^3+\cdots\right) &\mbox{}\\ \end{array} $$
Example
Find the first $5$ terms of the solution to the initial value problem $$ (4+x)y''+(1-3x)y'+(-1-4x)y=0,\,\,\,\,y(0)=2,\,\,y'(0)=1 $$
We will express out unknown solution as an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k.$
Then,
$$
\begin{array}{lll}
&\displaystyle (4+x)y''+(1-3x)y'+(-1-4x)y=0&\mbox{}\\
\implies &\displaystyle (4+x)\left(\sum_{k=0}^{\infty}a_k x^k\right)''+(1-3x)\left(\sum_{k=0}^{\infty}a_k x^k\right)'+(-1-4x)\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle (4+x)\sum_{k=2}^{\infty}k(k-1)a_k x^{k-2}+(1-3x)\sum_{k=1}^{\infty}ka_k x^{k-1}+(-1-4x)\sum_{k=0}^{\infty}a_k x^{k}=0&\mbox{}\\
\implies &\displaystyle 4\sum_{k=2}^{\infty}k(k-1)a_k x^{k-2}+x\sum_{k=2}^{\infty}k(k-1)a_k x^{k-2}+\sum_{k=1}^{\infty}ka_k x^{k-1}-3x\sum_{k=1}^{\infty}ka_k x^{k-1}-\sum_{k=0}^{\infty}a_k x^{k}-4x\sum_{k=0}^{\infty}a_k x^{k}=0&\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}4k(k-1)a_k x^{k-2}+\sum_{k=2}^{\infty}k(k-1)a_k x^{k-1}+\sum_{k=1}^{\infty}ka_k x^{k-1}-\sum_{k=1}^{\infty}3ka_k x^{k}-\sum_{k=0}^{\infty}a_k x^{k}-\sum_{k=0}^{\infty}4a_k x^{k+1}=0&\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}4(k+2)(k+1)a_{k+2} x^{k}+\sum_{k=1}^{\infty}(k+1)ka_{k+1} x^{k}+\sum_{k=0}^{\infty}(k+1)a_{k+1} x^{k}-\sum_{k=1}^{\infty}3ka_k x^{k}-\sum_{k=0}^{\infty}a_k x^{k}-\sum_{k=1}^{\infty}4a_{k-1} x^{k}=0&\mbox{}\\
\implies &\displaystyle \color{magenta}{8a_2}+\sum_{\color{magenta}{k=1}}^{\infty}4(k+2)(k+1)a_{k+2} x^{k}+\sum_{k=1}^{\infty}(k+1)ka_{k+1} x^{k}+\color{magenta}{a_1}+\sum_{\color{magenta}{k=1}}^{\infty}(k+1)a_{k+1} x^{k}-\sum_{k=1}^{\infty}3ka_k x^{k}-\color{magenta}{a_0}-\sum_{\color{magenta}{k=1}}^{\infty}a_k x^{k}-\sum_{k=1}^{\infty}4a_{k-1} x^{k}=0&\mbox{}\\
\implies &\displaystyle 8a_2+a_1-a_0+\sum_{k=1}^{\infty}[4(k+2)(k+1)a_{k+2} +(k+1)ka_{k+1}+(k+1)a_{k+1} -3ka_k-a_k -4a_{k-1}] x^{k}=0&\mbox{}\\
\implies &\displaystyle 8a_2+a_1-a_0+\sum_{k=1}^{\infty}[4(k+2)(k+1)a_{k+2} +((k+1)k+(k+1))a_{k+1} -(3k+1)a_k -4a_{k-1}] x^{k}=0&\mbox{}\\
\implies &\displaystyle 8a_2+a_1-a_0+\sum_{k=1}^{\infty}[4(k+2)(k+1)a_{k+2} +(k^2+2k+1)a_{k+1} -(3k+1)a_k -4a_{k-1}] x^{k}=0&\mbox{}\\
\end{array}
$$
For the above to be identically $0,$ is must be that
$$
8a_2+a_1-a_0=0
$$
or
$$
a_2=\frac{a_0-a_1}{8}
$$
and
$$
4(k+2)(k+1)a_{k+2} +(k^2+2k+1)a_{k+1} -(3k+1)a_k -4a_{k-1}=0
$$
or
$$
a_{k+2}=\frac{-(k^2+2k+1)a_{k+1} +(3k+1)a_k +4a_{k-1}}{4(k+2)(k+1)}
$$
where $k \geq 1.$
We now determine the values of $a_0$ and $a_1$ by satisfying the initial conditions.
Expressing $y(x)=\displaystyle \sum_{k=0}^{\infty}a_k x^k$ as $a_0+a_1 x+a_2 x^2+a_3 x^3+\cdots,$ satisfying the initial conditions is relatively straightforward. $$ \begin{array}{lll} &\displaystyle y(0)=2&\mbox{}\\ \implies &\displaystyle a_0+a_1\cdot 0+a_2\cdot 0^2+a_3\cdot 0^3+\cdots=2&\mbox{}\\ \implies &\displaystyle a_0=2&\mbox{}\\ \end{array} $$ and $$ \begin{array}{lll} &\displaystyle y'(0)=1&\mbox{}\\ \implies &\displaystyle a_1+2a_2\cdot 0+3a_3\cdot 0^2+\cdots=1&\mbox{}\\ \implies &\displaystyle a_1=1&\mbox{}\\ \end{array} $$ We may now have everything we need generate as many terms of the solution as we like.
From the above, $$ a_2=\frac{a_0-a_1}{8}=\frac{2-1}{8}=\frac{1}{8} $$ Using our recursion formula for $\color{magenta}{k=1},$ $$ \begin{array}{lll} \displaystyle a_3&\displaystyle=a_{\color{magenta}{1}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(\color{magenta}{1}^2+2(\color{magenta}{1})+1)a_{\color{magenta}{1}+1} +(3(\color{magenta}{1})+1)a_{\color{magenta}{1}} +4a_{\color{magenta}{1}-1}}{4(\color{magenta}{1}+2)(\color{magenta}{1}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4a_{2} +4a_1 +4a_{0}}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\cdot \frac{1}{8}+4(1)+4(2)}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{23}{48} &\mbox{}\\ \end{array} $$ Using our recursion formula for $\color{magenta}{k=2},$ $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=a_{\color{magenta}{2}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-((\color{magenta}{2})^2+2(\color{magenta}{2})+1)a_{\color{magenta}{2}+1} +(3(\color{magenta}{2})+1)a_{\color{magenta}{2}} +4a_{\color{magenta}{2}-1}}{4(\color{magenta}{2}+2)(\color{magenta}{2}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-9a_{3} +7a_2 +4a_{1}}{48} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-9\cdot \frac{23}{48} +7\cdot \frac{1}{8} +4(1)}{48} &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{256} &\mbox{}\\ \end{array} $$ Thus, the solution to our initial value problem showing the first $5$ terms is $$ y(x)=2+x+\frac{1}{8}x^2+\frac{23}{48}x^3+\frac{3}{256}x^4+\cdots $$
We now determine the values of $a_0$ and $a_1$ by satisfying the initial conditions.
Expressing $y(x)=\displaystyle \sum_{k=0}^{\infty}a_k x^k$ as $a_0+a_1 x+a_2 x^2+a_3 x^3+\cdots,$ satisfying the initial conditions is relatively straightforward. $$ \begin{array}{lll} &\displaystyle y(0)=2&\mbox{}\\ \implies &\displaystyle a_0+a_1\cdot 0+a_2\cdot 0^2+a_3\cdot 0^3+\cdots=2&\mbox{}\\ \implies &\displaystyle a_0=2&\mbox{}\\ \end{array} $$ and $$ \begin{array}{lll} &\displaystyle y'(0)=1&\mbox{}\\ \implies &\displaystyle a_1+2a_2\cdot 0+3a_3\cdot 0^2+\cdots=1&\mbox{}\\ \implies &\displaystyle a_1=1&\mbox{}\\ \end{array} $$ We may now have everything we need generate as many terms of the solution as we like.
From the above, $$ a_2=\frac{a_0-a_1}{8}=\frac{2-1}{8}=\frac{1}{8} $$ Using our recursion formula for $\color{magenta}{k=1},$ $$ \begin{array}{lll} \displaystyle a_3&\displaystyle=a_{\color{magenta}{1}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-(\color{magenta}{1}^2+2(\color{magenta}{1})+1)a_{\color{magenta}{1}+1} +(3(\color{magenta}{1})+1)a_{\color{magenta}{1}} +4a_{\color{magenta}{1}-1}}{4(\color{magenta}{1}+2)(\color{magenta}{1}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4a_{2} +4a_1 +4a_{0}}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\cdot \frac{1}{8}+4(1)+4(2)}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{23}{48} &\mbox{}\\ \end{array} $$ Using our recursion formula for $\color{magenta}{k=2},$ $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=a_{\color{magenta}{2}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-((\color{magenta}{2})^2+2(\color{magenta}{2})+1)a_{\color{magenta}{2}+1} +(3(\color{magenta}{2})+1)a_{\color{magenta}{2}} +4a_{\color{magenta}{2}-1}}{4(\color{magenta}{2}+2)(\color{magenta}{2}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-9a_{3} +7a_2 +4a_{1}}{48} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-9\cdot \frac{23}{48} +7\cdot \frac{1}{8} +4(1)}{48} &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{256} &\mbox{}\\ \end{array} $$ Thus, the solution to our initial value problem showing the first $5$ terms is $$ y(x)=2+x+\frac{1}{8}x^2+\frac{23}{48}x^3+\frac{3}{256}x^4+\cdots $$
Example
Solve the equation $x^2y''-y=0$ using power series at $x_0=0.$
Expressing the unknown solution as an infinite series, $\displaystyle \sum_{k=0}^{\infty}a_k x^k,$ we have
$$
\begin{array}{lll}
&\displaystyle x^2y''-y=0&\mbox{}\\
\implies &\displaystyle x^2\left(\sum_{k=0}^{\infty}a_k x^k\right)''-\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle x^2\sum_{k=2}^{\infty}k(k-1)a_k x^{k-2}-\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k x^{k}-\sum_{k=0}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k x^{k}-a_0-a_1x-\sum_{k=2}^{\infty}a_k x^k=0&\mbox{}\\
\implies &\displaystyle -a_0-a_1x+\sum_{k=2}^{\infty}[k(k-1)a_k -a_k] x^k=0&\mbox{}\\
\implies &\displaystyle -a_0-a_1x+\sum_{k=2}^{\infty}[k(k-1) -1]a_k x^k=0&\mbox{}\\
\implies &\displaystyle -a_0-a_1x+\sum_{k=2}^{\infty}(k^2-k-1)a_k x^k=0&\mbox{}\\
\end{array}
$$
In order for the above to be identically $0$ for all $x,$ it must be that
$$
-a_0-a_1x=0
$$
for all $x$ and
$$
(k^2-k-1)a_k=0
$$
for all $k\geq 2.$
The only way $-a_0-a_1x$ could be $0$ for all $x$ is if $a_1=0,$ and that would force $a_0$ to also be $0.$
Also, since $k^2-k-1\neq 0$ for any $k,$ the only way $(k^2-k-1)a_k$ could be zero for $k\geq 2$ is if $a_k=0.$
Consequently, $y(x)\equiv 0$ is the only solution that we can find using our current method.
However, there are more solutions.
What happened??????????????????????
The only way $-a_0-a_1x$ could be $0$ for all $x$ is if $a_1=0,$ and that would force $a_0$ to also be $0.$
Also, since $k^2-k-1\neq 0$ for any $k,$ the only way $(k^2-k-1)a_k$ could be zero for $k\geq 2$ is if $a_k=0.$
Consequently, $y(x)\equiv 0$ is the only solution that we can find using our current method.
However, there are more solutions.
What happened??????????????????????
Ordinary Points versus Singular Points
For the equation $$ p(x)y''+q(x)y'+r(x)y=0 $$ suppose we want to find a series solution centered at $x_0.$
If $p(x_0)\neq 0,$ then $x_0$ is called an ordinary point.
If $p(x_0)=0,$ then $x_0$ is called an singular point.
Note: Finding series solutions at singular points is harder, but in many cases it is possible. It requires the methods which we will not cover in this class. One such method is "The Method of Frobenius."
Another option is to find a series expansion around an ordinary point.
Example
Find the first $5$ terms of the general power series solution to $x^2y''-y=0$ centered at $x_0=1.$
We express the unknown solution as an infinite series about $x_0=1,$ that is $\displaystyle \sum_{k=0}^{\infty}a_k (x-1)^k.$
$$
\begin{array}{lll}
&\displaystyle x^2y''-y=0&\mbox{}\\
\implies &\displaystyle x^2\left(\sum_{k=0}^{\infty}a_k (x-1)^k\right)''-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\
\implies &\displaystyle x^2\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\
\end{array}
$$
Now, the coefficient $x^2$ does not play nice with the powers of the form $(x-1)^k.$
So, we express $x^2$ as a sum of powers of $x-1$ by performing a Taylor expansion around $x_0=1.$ $$ \begin{array}{lll} \displaystyle p(x)&\displaystyle=x^2 &\mbox{}\\ \displaystyle p'(x)&\displaystyle=2x &\mbox{}\\ \displaystyle p''(x)&\displaystyle=2 &\mbox{}\\ \displaystyle p^{(k)}(x)&\displaystyle=0 &\mbox{for $k\geq 3$}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle \frac{p(1)}{0!}&\displaystyle=\frac{1}{1}=1 &\mbox{}\\ \displaystyle \frac{p'(1)}{1!}&\displaystyle=\frac{2}{1}=2 &\mbox{}\\ \displaystyle \frac{p''(1)}{2!}&\displaystyle=\frac{2}{2}=1 &\mbox{}\\ \displaystyle \frac{p^{(k)}(1)}{k!}&\displaystyle=\frac{0}{k!}=0 &\mbox{for $k\geq 3$}\\ \end{array} $$ Thus, $p(x)=x^2=1+2(x-1)+(x-1)^2.$
We may now proceed with our first calculation. $$ \begin{array}{lll} &\displaystyle x^2y''-y=0&\mbox{}\\ \implies &\displaystyle x^2\left(\sum_{k=0}^{\infty}a_k (x-1)^k\right)''-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle x^2\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \left[1+2(x-1)+(x-1)^2\right]\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+2(x-1)\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+(x-1)^2\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+\sum_{k=2}^{\infty}2k(k-1)a_k (x-1)^{k-1}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=0}^{\infty}(k+2)(k+1)a_{k+2} (x-1)^{k}+\sum_{k=1}^{\infty}2(k+1)ka_{k+1} (x-1)^{k}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \color{magenta}{2a_2+6a_3(x-1)}+\sum_{\color{magenta}{k=2}}^{\infty}(k+2)(k+1)a_{k+2} (x-1)^{k}+\color{magenta}{4a_2(x-1)}+\sum_{\color{magenta}{k=2}}^{\infty}2(k+1)ka_{k+1} (x-1)^{k}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}\color{magenta}{-a_0-a_1(x-1)}-\sum_{\color{magenta}{k=2}}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle 2a_2+6a_3(x-1)+4a_2(x-1)-a_0-a_1(x-1)+\sum_{k=2}^{\infty}\left[(k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k\right] (x-1)^k=0&\mbox{}\\ \implies &\displaystyle 2a_2-a_0+(6a_3+4a_2-a_1)(x-1)+\sum_{k=2}^{\infty}\left[(k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k\right] (x-1)^k=0&\mbox{}\\ \end{array} $$ For the above to be identically $0,$ we must have $$ 2a_2-a_0=0 $$ $$ 6a_3+4a_2-a_1=0 $$ and $$ (k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k=0 $$ or $$ a_{k+2}=\frac{-2(k+1)ka_{k+1}-k(k-1)a_k+a_k}{(k+2)(k+1)}=\frac{-2(k+1)ka_{k+1}-(k^2-k-1)a_k}{(k+2)(k+1)} $$ for $k \geq 2.$
Letting $a_0$ and $a_1$ be undetermined constants, $$ a_2=\frac{1}{2}a_0 $$ and $$ \begin{array}{lll} \displaystyle a_3 &\displaystyle=\frac{-4a_2+a_1}{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\left(\frac{1}{2}a_0\right)+a_1}{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2a_0+a_1}{6} &\mbox{}\\ \end{array} $$ From here we may generate as many terms as we like. $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=a_{\color{magenta}{2}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2(\color{magenta}{2}+1)(\color{magenta}{2})a_{\color{magenta}{2}+1}-(\color{magenta}{2}^2-\color{magenta}{2}-1)a_{\color{magenta}{2}}}{(\color{magenta}{2}+2)(\color{magenta}{2}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-12a_3-a_2}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-12\left(\frac{-2a_0+a_1}{6}\right)-\frac{1}{2}a_0}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2\left(-2a_0+a_1\right)-\frac{1}{2}a_0}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\left(-2a_0+a_1\right)-a_0}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8a_0-4a_1-a_0}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{7a_0-4a_1}{24} &\mbox{}\\ \end{array} $$ Our series expansion, showing the first $5$ terms is $$ y(x)=a_0+a_1(x-1)+\frac{a_0}{2}(x-1)^2+\frac{-2a_0+a_1}{6}(x-1)^3+\frac{7a_0-4a_1}{24}(x-1)^4+\cdots $$ and we may choose $a_0$ and $a_1$ to satisfy initial conditions if necessary.
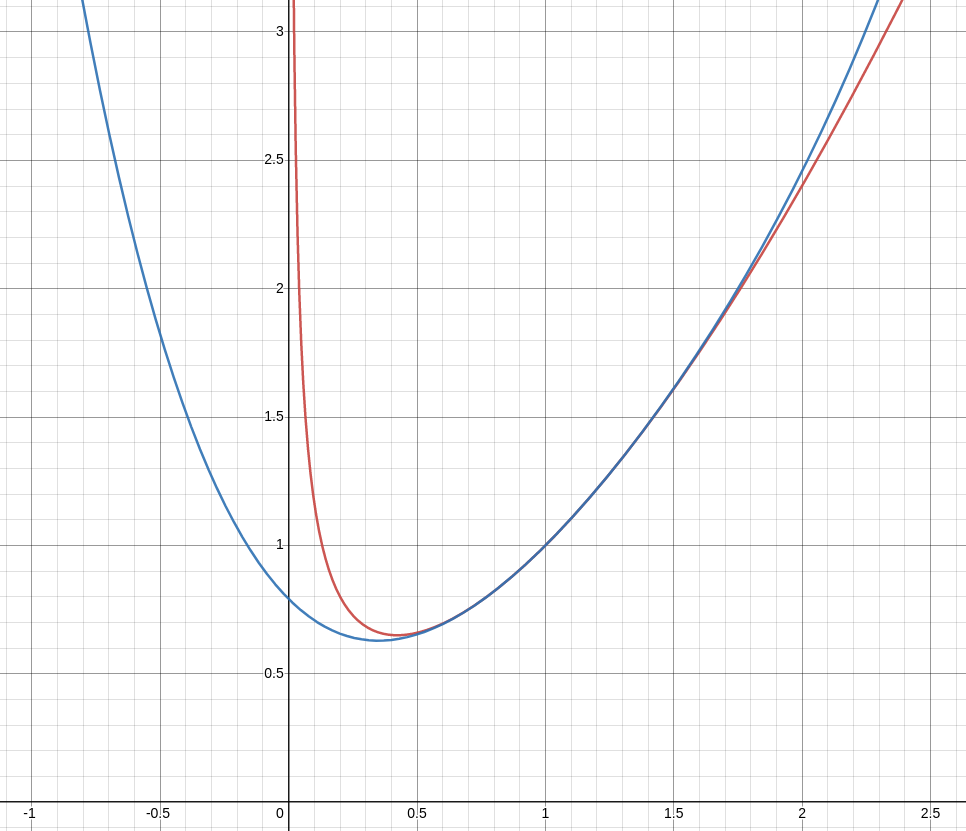
To confirm our calculations, let's choose initial conditions $y(1)=1$ and $y'(1)=1$ (that is, $a_0=1$ and $a_1=1$) and compare the graph of the exact solution and the $4$th-degree Taylor polynomial approximation $\displaystyle \color{#3e7bb7}{P_4(x)=1+(x-1)+\frac{1}{2}(x-1)^2-\frac{1}{6}(x-1)^3+\frac{1}{8}(x-1)^4}.$
So, we express $x^2$ as a sum of powers of $x-1$ by performing a Taylor expansion around $x_0=1.$ $$ \begin{array}{lll} \displaystyle p(x)&\displaystyle=x^2 &\mbox{}\\ \displaystyle p'(x)&\displaystyle=2x &\mbox{}\\ \displaystyle p''(x)&\displaystyle=2 &\mbox{}\\ \displaystyle p^{(k)}(x)&\displaystyle=0 &\mbox{for $k\geq 3$}\\ \end{array} $$ Then $$ \begin{array}{lll} \displaystyle \frac{p(1)}{0!}&\displaystyle=\frac{1}{1}=1 &\mbox{}\\ \displaystyle \frac{p'(1)}{1!}&\displaystyle=\frac{2}{1}=2 &\mbox{}\\ \displaystyle \frac{p''(1)}{2!}&\displaystyle=\frac{2}{2}=1 &\mbox{}\\ \displaystyle \frac{p^{(k)}(1)}{k!}&\displaystyle=\frac{0}{k!}=0 &\mbox{for $k\geq 3$}\\ \end{array} $$ Thus, $p(x)=x^2=1+2(x-1)+(x-1)^2.$
We may now proceed with our first calculation. $$ \begin{array}{lll} &\displaystyle x^2y''-y=0&\mbox{}\\ \implies &\displaystyle x^2\left(\sum_{k=0}^{\infty}a_k (x-1)^k\right)''-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle x^2\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \left[1+2(x-1)+(x-1)^2\right]\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+2(x-1)\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+(x-1)^2\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k-2}+\sum_{k=2}^{\infty}2k(k-1)a_k (x-1)^{k-1}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \sum_{k=0}^{\infty}(k+2)(k+1)a_{k+2} (x-1)^{k}+\sum_{k=1}^{\infty}2(k+1)ka_{k+1} (x-1)^{k}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}-\sum_{k=0}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle \color{magenta}{2a_2+6a_3(x-1)}+\sum_{\color{magenta}{k=2}}^{\infty}(k+2)(k+1)a_{k+2} (x-1)^{k}+\color{magenta}{4a_2(x-1)}+\sum_{\color{magenta}{k=2}}^{\infty}2(k+1)ka_{k+1} (x-1)^{k}+\sum_{k=2}^{\infty}k(k-1)a_k (x-1)^{k}\color{magenta}{-a_0-a_1(x-1)}-\sum_{\color{magenta}{k=2}}^{\infty}a_k (x-1)^k=0&\mbox{}\\ \implies &\displaystyle 2a_2+6a_3(x-1)+4a_2(x-1)-a_0-a_1(x-1)+\sum_{k=2}^{\infty}\left[(k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k\right] (x-1)^k=0&\mbox{}\\ \implies &\displaystyle 2a_2-a_0+(6a_3+4a_2-a_1)(x-1)+\sum_{k=2}^{\infty}\left[(k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k\right] (x-1)^k=0&\mbox{}\\ \end{array} $$ For the above to be identically $0,$ we must have $$ 2a_2-a_0=0 $$ $$ 6a_3+4a_2-a_1=0 $$ and $$ (k+2)(k+1)a_{k+2}+2(k+1)ka_{k+1}+k(k-1)a_k-a_k=0 $$ or $$ a_{k+2}=\frac{-2(k+1)ka_{k+1}-k(k-1)a_k+a_k}{(k+2)(k+1)}=\frac{-2(k+1)ka_{k+1}-(k^2-k-1)a_k}{(k+2)(k+1)} $$ for $k \geq 2.$
Letting $a_0$ and $a_1$ be undetermined constants, $$ a_2=\frac{1}{2}a_0 $$ and $$ \begin{array}{lll} \displaystyle a_3 &\displaystyle=\frac{-4a_2+a_1}{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\left(\frac{1}{2}a_0\right)+a_1}{6} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2a_0+a_1}{6} &\mbox{}\\ \end{array} $$ From here we may generate as many terms as we like. $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=a_{\color{magenta}{2}+2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2(\color{magenta}{2}+1)(\color{magenta}{2})a_{\color{magenta}{2}+1}-(\color{magenta}{2}^2-\color{magenta}{2}-1)a_{\color{magenta}{2}}}{(\color{magenta}{2}+2)(\color{magenta}{2}+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-12a_3-a_2}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-12\left(\frac{-2a_0+a_1}{6}\right)-\frac{1}{2}a_0}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-2\left(-2a_0+a_1\right)-\frac{1}{2}a_0}{12} &\mbox{}\\ \displaystyle &\displaystyle=\frac{-4\left(-2a_0+a_1\right)-a_0}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{8a_0-4a_1-a_0}{24} &\mbox{}\\ \displaystyle &\displaystyle=\frac{7a_0-4a_1}{24} &\mbox{}\\ \end{array} $$ Our series expansion, showing the first $5$ terms is $$ y(x)=a_0+a_1(x-1)+\frac{a_0}{2}(x-1)^2+\frac{-2a_0+a_1}{6}(x-1)^3+\frac{7a_0-4a_1}{24}(x-1)^4+\cdots $$ and we may choose $a_0$ and $a_1$ to satisfy initial conditions if necessary.
To confirm our calculations, let's choose initial conditions $y(1)=1$ and $y'(1)=1$ (that is, $a_0=1$ and $a_1=1$) and compare the graph of the exact solution and the $4$th-degree Taylor polynomial approximation $\displaystyle \color{#3e7bb7}{P_4(x)=1+(x-1)+\frac{1}{2}(x-1)^2-\frac{1}{6}(x-1)^3+\frac{1}{8}(x-1)^4}.$

Bonus Problems!
Example
Solve the non-homogenous equation $y'-2xy=1$ using a power series at $x_0=0.$
To solve this equation, we will express out unknown solution as an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k.$
Then,
$$
\begin{array}{lll}
&\displaystyle y'-2xy=1 &\mbox{}\\
\implies &\displaystyle \left(\sum_{k=0}^{\infty}a_k x^k\right)'-2x\sum_{k=0}^{\infty}a_k x^k=1&\mbox{}\\
\implies &\displaystyle \sum_{k=1}^{\infty}a_k k x^{k-1}-2x\sum_{k=0}^{\infty}a_k x^k=1&\mbox{differentiating term by term}\\
\implies &\displaystyle a_1+\sum_{k=2}^{\infty}a_k k x^{k-1}-\sum_{k=0}^{\infty}2 a_k x^{k+1}=1&\mbox{peeling off the first term of the first series}\\
\implies &\displaystyle a_1+\sum_{k=1}^{\infty}a_{k+1} (k+1) x^{k}-\sum_{k=1}^{\infty}2 a_{k-1} x^{k}=1&\mbox{re-indexing both sums}\\
\implies &\displaystyle a_1+\sum_{k=1}^{\infty}\left[a_{k+1} (k+1) x^{k}-2 a_{k-1}\right] x^{k}=1&\mbox{using properties of series}\\
\implies &\displaystyle (a_1-1)+\sum_{k=1}^{\infty}\left((k+1)a_{k+1} -2 a_{k-1}\right) x^{k}=0&\mbox{}\\
\end{array}
$$
The only way the above series can be zero for all $x$ is if $a_1-1=0$ and $(k+1)a_{k+1}-2 a_{k-1}=0$ for all $k \geq 1.$
From these equations, we may determine the coefficients $a_1, a_2, a_3, \ldots$
From the first equation, we know that $a_1=1.$
For the second equation which is a recurrence relation, we rewrite it as $ka_{k} -2 a_{k-2}=0$ for all $k\geq 2,$ which more conveniently becomes $$ a_{k} =\frac{2}{k}a_{k-2} \mbox{ for all } k\geq 2 $$ Then, $$ \begin{array}{lll} \displaystyle a_0 & &\mbox{an unknown constant}\\ a_1 &=\displaystyle 1&\mbox{}\\ a_2 &=\displaystyle \frac{2}{2}a_{0}=a_0&\mbox{}\\ a_3 &=\displaystyle \frac{2}{3}a_{1}=\frac{2}{3}&\mbox{}\\ a_4 &=\displaystyle \frac{2}{4} a_{2}=\frac{1}{2}a_2=\frac{1}{2}a_0&\mbox{}\\ a_5 &=\displaystyle \frac{2}{5} a_{3}=\frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_6 &=\displaystyle \frac{2}{6} a_{4}=\frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_7 &=\displaystyle \frac{2}{7} a_{5}=\frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_8 &=\displaystyle \frac{2}{8} a_{6}=\frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_9 &=\displaystyle \frac{2}{9} a_{7}=\frac{2}{9}\cdot \frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_{10} &=\displaystyle \frac{2}{10} a_{8}=\frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ &\vdots& \end{array} $$ From the above we can see the pattern: $$ a_{2k+1}= \frac{2}{(2k+1)}\cdots \frac{2}{9}\cdot \frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}=\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)} $$ and $$ a_{2k}=\frac{1}{k}\cdots \frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0=\frac{1}{k!}a_0 $$ Our solution is then $$ \begin{array}{ll} y&=\displaystyle \sum_{k=0}^{\infty}a_k x^k\\ &=\displaystyle \sum_{k=0}^{\infty}a_{2k}x^{2k}+\sum_{k=0}^{\infty}a_{2k+1}x^{2k+1}\\ &=\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!}a_0 x^{2k}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}\\ &=\displaystyle a_0\sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}\\ \end{array} $$ We note that $a_0$ is the constant of our general solution. We also recognize the series $\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}$ as none other than $e^{x^2}.$ Thus, $$ y=a_0e^{x^2}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1} $$ We see that $y_h=a_0e^{x^2}$ solves the homogeneous equation (our first example) and $\displaystyle y_p=\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}$ is the particular solution.
From these equations, we may determine the coefficients $a_1, a_2, a_3, \ldots$
From the first equation, we know that $a_1=1.$
For the second equation which is a recurrence relation, we rewrite it as $ka_{k} -2 a_{k-2}=0$ for all $k\geq 2,$ which more conveniently becomes $$ a_{k} =\frac{2}{k}a_{k-2} \mbox{ for all } k\geq 2 $$ Then, $$ \begin{array}{lll} \displaystyle a_0 & &\mbox{an unknown constant}\\ a_1 &=\displaystyle 1&\mbox{}\\ a_2 &=\displaystyle \frac{2}{2}a_{0}=a_0&\mbox{}\\ a_3 &=\displaystyle \frac{2}{3}a_{1}=\frac{2}{3}&\mbox{}\\ a_4 &=\displaystyle \frac{2}{4} a_{2}=\frac{1}{2}a_2=\frac{1}{2}a_0&\mbox{}\\ a_5 &=\displaystyle \frac{2}{5} a_{3}=\frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_6 &=\displaystyle \frac{2}{6} a_{4}=\frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_7 &=\displaystyle \frac{2}{7} a_{5}=\frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_8 &=\displaystyle \frac{2}{8} a_{6}=\frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ a_9 &=\displaystyle \frac{2}{9} a_{7}=\frac{2}{9}\cdot \frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}&\mbox{}\\ a_{10} &=\displaystyle \frac{2}{10} a_{8}=\frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0&\mbox{}\\ &\vdots& \end{array} $$ From the above we can see the pattern: $$ a_{2k+1}= \frac{2}{(2k+1)}\cdots \frac{2}{9}\cdot \frac{2}{7}\cdot \frac{2}{5}\cdot \frac{2}{3}=\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)} $$ and $$ a_{2k}=\frac{1}{k}\cdots \frac{1}{5}\cdot \frac{1}{4}\cdot \frac{1}{3}\cdot \frac{1}{2}a_0=\frac{1}{k!}a_0 $$ Our solution is then $$ \begin{array}{ll} y&=\displaystyle \sum_{k=0}^{\infty}a_k x^k\\ &=\displaystyle \sum_{k=0}^{\infty}a_{2k}x^{2k}+\sum_{k=0}^{\infty}a_{2k+1}x^{2k+1}\\ &=\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!}a_0 x^{2k}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}\\ &=\displaystyle a_0\sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}\\ \end{array} $$ We note that $a_0$ is the constant of our general solution. We also recognize the series $\displaystyle \sum_{k=0}^{\infty} \frac{1}{k!} x^{2k}$ as none other than $e^{x^2}.$ Thus, $$ y=a_0e^{x^2}+\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1} $$ We see that $y_h=a_0e^{x^2}$ solves the homogeneous equation (our first example) and $\displaystyle y_p=\sum_{k=0}^{\infty}\frac{2^{k}}{3\cdot 5 \cdot 7 \cdots (2k+1)}x^{2k+1}$ is the particular solution.
Example
Find the first $4$ non-zero terms of the series solution centered at $x_0=0$ of the non-homogenous IVP $$ y''-xy=\frac{1}{1-x},\,\,\,y(0)=0,\,\,y'(0)=0 $$
Letting our solution be an infinite series $\displaystyle \sum_{k=0}^{\infty}a_k x^k,$ we have
$$
\begin{array}{lll}
&\displaystyle y''-xy=\frac{1}{1-x} &\mbox{}\\
\implies &\displaystyle \left(\sum_{k=0}^{\infty}a_k x^k\right)''-x\sum_{k=0}^{\infty}a_k x^k=\sum_{k=0}^{\infty} x^k &\mbox{}\\
\implies &\displaystyle \sum_{k=2}^{\infty}k(k-1)a_k x^{k-2}-\sum_{k=0}^{\infty}a_k x^{k+1}-\sum_{k=0}^{\infty} x^k=0 &\mbox{}\\
\implies &\displaystyle \sum_{k=0}^{\infty}(k+2)(k+1)a_{k+2} x^{k}-\sum_{k=1}^{\infty}a_{k-1} x^{k}-\sum_{k=0}^{\infty} x^k=0 &\mbox{}\\
\implies &\displaystyle 2a_2+\sum_{k=1}^{\infty}(k+2)(k+1)a_{k+2} x^{k}-\sum_{k=1}^{\infty}a_{k-1} x^{k}-1-\sum_{k=1}^{\infty} x^k=0 &\mbox{}\\
\implies &\displaystyle 2a_2-1+\sum_{k=1}^{\infty}[(k+2)(k+1)a_{k+2}-a_{k-1}-1] x^k=0 &\mbox{}\\
\end{array}
$$
For the above to be identically $0$ for all $x,$ it must be that
$$
2a_2-1=0
$$
and
$$
(k+2)(k+1)a_{k+2} -a_{k-1}-1=0
$$
that is,
$$
a_{k+2}=\frac{a_{k-1}+1}{(k+2)(k+1)}
$$
for all $k\geq 1.$
The initial conditions give us that $a_0=0$ and $a_1=0,$ and the above gives that $\displaystyle a_2=\frac{1}{2}.$
Using our recursion formula, we may now generate as many terms as we like. $$ \begin{array}{lll} \displaystyle a_3&\displaystyle=\frac{a_{0}+1}{(1+2)(1+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{0+1}{(3)(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{6} &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=\frac{a_{1}+1}{(2+2)(2+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{0+1}{(4)(3)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{12} &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle a_5&\displaystyle=\frac{a_{2}+1}{(3+2)(3+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\frac{1}{2}+1}{(5)(4)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{40} &\mbox{}\\ \end{array} $$ Thus, our series solution, showing the first $4$ non-zero terms is $$ y(x)=\frac{1}{2}x^{2}+\frac{1}{6}x^{3}+\frac{1}{12}x^{4}+\frac{3}{40}x^{5}+\cdots $$
The initial conditions give us that $a_0=0$ and $a_1=0,$ and the above gives that $\displaystyle a_2=\frac{1}{2}.$
Using our recursion formula, we may now generate as many terms as we like. $$ \begin{array}{lll} \displaystyle a_3&\displaystyle=\frac{a_{0}+1}{(1+2)(1+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{0+1}{(3)(2)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{6} &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle a_4&\displaystyle=\frac{a_{1}+1}{(2+2)(2+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{0+1}{(4)(3)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{12} &\mbox{}\\ \end{array} $$ $$ \begin{array}{lll} \displaystyle a_5&\displaystyle=\frac{a_{2}+1}{(3+2)(3+1)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{\frac{1}{2}+1}{(5)(4)} &\mbox{}\\ \displaystyle &\displaystyle=\frac{3}{40} &\mbox{}\\ \end{array} $$ Thus, our series solution, showing the first $4$ non-zero terms is $$ y(x)=\frac{1}{2}x^{2}+\frac{1}{6}x^{3}+\frac{1}{12}x^{4}+\frac{3}{40}x^{5}+\cdots $$