Power Series

Power Series

Power series is in itself a marvellous, beautiful, and useful topic in many ways.

It enables us to look at old things in a new light and will give us analytical tools which allow us to solve problems that previously we couldn't.

In particular, a series representation is like "unzipping" a function and looking at its "DNA", revealing how a function behaves and is related to other functions.

Here we will learn the basics of power series to solve differential equations.

A power series is essentially an "infinite polynomial."

A More Formal Introduction

An expression of the form $\displaystyle \sum_{k=0}^{\infty}a_kx^k$ is a power series centered at $x=0.$

An expression of the form $\displaystyle \sum_{k=0}^{\infty}a_k(x-x_0)^k$ is a power series centered at $x=x_0.$

Note: Power series are often indexed starting at $k=0$ since it's prettier. The assumption we must make is that $x^0=1$ and $(x-x_0)^0=1$ even if $x=0$ or $x-x_0=0.$

A More Formal Introduction

A series $\displaystyle \sum_{k=0}^{\infty}a_k(x-x_0)^k$ is said to converge at $x$ if the limit of the partial sums converges, that is, if $$ \lim_{n\rightarrow\infty}S_n(x)=\lim_{n\rightarrow\infty}\sum_{k=0}^{n}a_k(x-x_0)^k $$ converges to some real number.

A series that does not converge is said to diverge.

Example

The power series $\displaystyle \sum_{k=0}^{\infty}x^k$ converges to the number $\displaystyle \frac{1}{1-x}$ for any $x$ in the interval $(-1,1).$

A Big Idea

The above illustrates that certain functions say can be represented by the power series over certain intervals.

Example

$\displaystyle \color{blue}{f(x)=\frac{1}{1-x}}=\color{red}{\sum_{k=0}^{\infty}x^k}$ on the interval $(-1,1).$

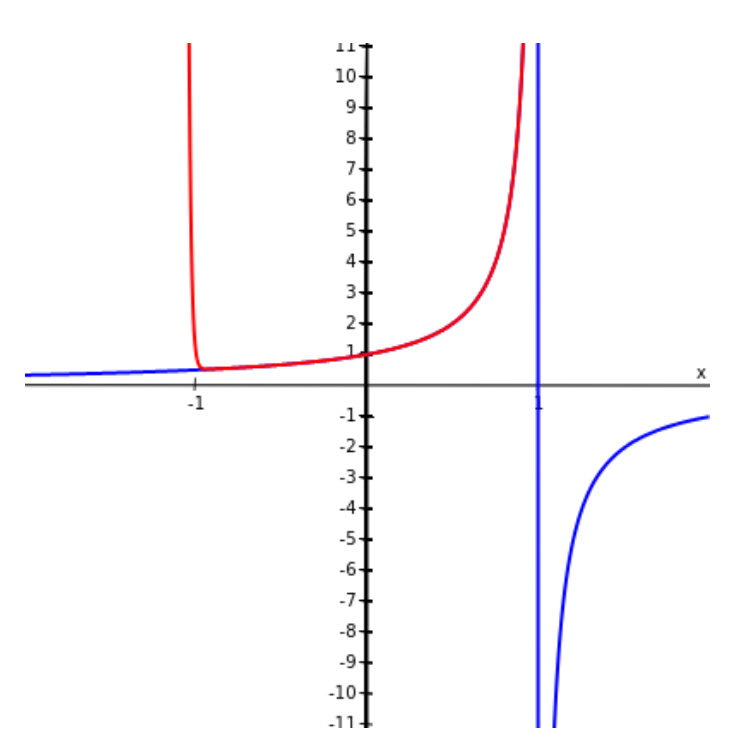
Example: The function $\displaystyle f(x)=e^x$ can be represented by the power series $\displaystyle \sum_{k=0}^{\infty}\frac{1}{k!}x^{k}.$

Example: The function $\displaystyle f(x)=\sin x$ can be represented by the power series $\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1}.$

Some Common Series Representations $$ \begin{array}{lll} \displaystyle &\displaystyle &\mbox{}\\ \displaystyle \sin x=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{(2k+1)!}\,\, \mbox{ on }\,\, (-\infty,\infty) &&\displaystyle \cos x=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k}}{(2k)!}\,\, \mbox{ on }\,\, (-\infty,\infty) \\ \displaystyle e^x=\sum_{k=0}^{\infty}\frac{x^{k}}{k!}\,\, \mbox{ on }\,\, (-\infty,\infty) &&\displaystyle \ln x =\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}(x-1)^{k}\,\, \mbox{ on }\,\, (0,2] \\ \displaystyle \tan^{-1} x=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{2k+1}\,\, \mbox{ on }\,\, [-1,1] &&\displaystyle \frac{1}{1-x} =\sum_{k=1}^{\infty}x^{k} \,\, \mbox{ on }\,\, (-1,1) \\ \displaystyle \sinh x=\sum_{k=0}^{\infty}\frac{x^{2k+1}}{(2k+1)!} \,\, \mbox{ on }\,\, (-\infty,\infty)&&\displaystyle \cosh x=\sum_{k=0}^{\infty}\frac{x^{2k}}{(2k)!}\,\, \mbox{ on }\,\, (-\infty,\infty) \\ \end{array} $$

Yeah, but how do we find the series representation of a function?

Taylor Series

Suppose we want to approximate a function $f(x)$ by a polynomial.

The $n$th-degree Taylor approximation $P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots+a_n(x-x_0)^n$ at $x_0$ says that the best way to do this is to make sure the function value and all the derivatives agree.

This ensures that $P_n(x)$ behaves very much like $f(x)$ at $x_0.$

For example, a function $f(x)$ and its tangent line approximation have the same function value and first derivative.

Taylor Series

The $n$th-degree Taylor approximation of $f(x)$ at $x_0$ is the polynomial $$P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots+a_n(x-x_0)^n$$ which makes the function values and all derivatives of $f(x)$ and $P_n(x)$ agree at $x_0.$

That is, $$ \begin{array}{l} P_n(x_0)=f(x_0)\\ P_n'(x_0)=f'(x_0)\\ P_n''(x_0)=f''(x_0)\\ \,\,\,\,\,\vdots\\ P_n^{(n)}(x_0)=f^{(n)}(x_0)\\ \end{array} $$

Taylor Series

Since $$ \begin{array}{l} P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots+a_n(x-x_0)^n\\ P_n'(x)=a_1+2a_2(x-x_0)+\cdots+na_n(x-x_0)^{n-1}\\ P_n''(x)=2a_2+\cdots+n(n-1)a_n(x-x_0)^{n-2}\\ \,\,\,\,\,\vdots\\ P_n^{(n)}(x)=n(n-1)(n-2)\cdots \cdot 3 \cdot 2\cdot 1 \cdot a_n\\ \end{array} $$ we have by the previous slide that $$ \begin{array}{l} a_0=P_n(x_0)=f(x_0)\\ a_1=P_n'(x_0)=f'(x_0)\\ 2a_2=P_n''(x_0)=f''(x_0)\\ \,\,\,\,\,\vdots\\ n(n-1)(n-2)\cdots 2\cdot 1 \cdot a_n=P_n^{(n)}(x_0)=f^{(n)}(x_0)\\ \end{array} $$

Taylor Series

Consequently, the $k$th coefficient of the $n$th Taylor polynomial at $x_0$ is $$ a_k=\frac{f^{(k)}(x_0)}{k\cdot (k-1)\cdots 3\cdot 2 \cdot 1}=\frac{f^{(k)}(x_0)}{k!} $$ That is, $$ P_n(x_0)=\sum_{k=0}^{n}a_k(x-x_0)^k=\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k $$ Note: $0!=1$

Taylor Series

If $f(x)$ has infinitely many derivatives at $x_0,$ then series representation of $f(x)$ at $x_0$ is $$ f(x)=\lim_{n\rightarrow\infty}\sum_{k=0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k=\sum_{k=0}^{\infty}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k $$ This series may converge for all $x,$ but it may only converge for $x$ in a finite interval near $x_0.$

Example

Find the Taylor series expansion of $f(x)=\sin x.$

Note: The Taylor series centered at $x_0=0$ is called the Maclaurin series.

We first note that $$ \begin{array}{lll} f(x)&=&\sin x\\ f'(x)&=&\cos x\\ f''(x)&=&-\sin x\\ f'''(x)&=&-\cos x\\ f^{(4)}(x)&=&\sin x\\ f^{(5)}(x)&=&\cos x\\ f^{(6)}(x)&=&-\sin x\\ f^{(7)}(x)&=&-\cos x\\ &\vdots& \end{array} $$ Thus, the coefficients of the Maclaurin series expansion are $$ \begin{array}{lll} \displaystyle a_0&=\displaystyle \frac{f^{(0)}(0)}{0!}=f(0)=\sin 0 =0\\ \displaystyle a_1&=\displaystyle \frac{f^{(1)}(0)}{1!}=f'(0)=\cos 0 =1\\ \displaystyle a_2&=\displaystyle \frac{f^{(2)}(0)}{2!}=\frac{f''(0)}{2}=\frac{-\sin 0}{2} =0\\ \displaystyle a_3&=\displaystyle \frac{f^{(3)}(0)}{3!}=\frac{f'''(0)}{3!}=\frac{-\cos 0}{3!} =-\frac{1}{3!}\\ \displaystyle a_4&=\displaystyle \frac{f^{(4)}(0)}{4!}=\frac{\sin 0}{4!} =0\\ \displaystyle a_5&=\displaystyle \frac{f^{(5)}(0)}{5!}=\frac{\cos 0}{5!} =\frac{1}{5!}\\ \displaystyle a_6&=\displaystyle \frac{f^{(6)}(0)}{6!}=\frac{-\sin 0}{6!} =\frac{0}{6!}=0\\ \displaystyle a_7&=\displaystyle \frac{f^{(7)}(0)}{7!}=\frac{-\cos 0}{7!} =-\frac{1}{7!}\\ &\vdots& \end{array} $$ The Maclaurin series expansion is then $$ \begin{array}{lll} \displaystyle \sin x&=\displaystyle \sum_{k=0}^{\infty}\frac{f^{(k)}(0)}{k!}x^{k}\\ &=\displaystyle \frac{f(0)}{0!}+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5+\cdots+\frac{f^{(k)}(0)}{k!}x^k+\cdots&\\ &=\displaystyle 0+x+0x^2-\frac{1}{3!}x^3+0x^4+\frac{1}{5!}x^5+0x^6-\frac{1}{7!}x^7+\cdots&\\ &=\displaystyle x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots&\\ &=\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1}&\\ \end{array} $$

Example

Find the Taylor series expansion of $f(x)=\ln(x)$ at $x_0=1.$

We first note that $$ \begin{array}{lll} f(x)&=&\ln x\\ f'(x)&=&\displaystyle \frac{1}{x}=\frac{0!}{x}\\ f''(x)&=&\displaystyle -\frac{1}{x^2}=-\frac{1!}{x^2}\\ f'''(x)&=&\displaystyle \frac{2}{x^3}=\frac{2!}{x^3}\\ f^{(4)}(x)&=&\displaystyle -\frac{2\cdot 3}{x^4}=-\frac{3!}{x^4}\\ f^{(5)}(x)&=&\displaystyle \frac{2\cdot 3\cdot 4}{x^5}=\frac{4!}{x^5}\\ f^{(6)}(x)&=&\displaystyle -\frac{2\cdot 3\cdot 4\cdot 5}{x^6}=-\frac{5!}{x^6}\\ f^{(7)}(x)&=&\displaystyle \frac{2\cdot 3 \cdot 4 \cdot 5 \cdot 6}{x^7}=\frac{6!}{x^7}\\ &\vdots& \end{array} $$ Thus, $\displaystyle f^{(k)}(x)=(-1)^{k+1}\frac{(k-1)!}{x^k}$ for $k \geq 1.$

Since we're expanding at $x_0=1,$ we have $\displaystyle f^{(k)}(1)=(-1)^{k+1}(k-1)!$ for $k\geq 1.$

The Taylor series expansion around $x_0=1$ is then $$ \begin{array}{lll} \displaystyle \ln x&=\displaystyle \sum_{k=0}^{\infty}\frac{f^{(k)}(1)}{k!}(x-1)^{k}\\ &=\displaystyle \frac{f(1)}{0!}+\frac{f'(1)}{1!}(x-1)+\frac{f''(1)}{2!}(x-1)^2+\frac{f'''(1)}{3!}(x-1)^3+\frac{f^{(4)}(1)}{4!}(x-1)^4+\frac{f^{(5)}(1)}{5!}(x-1)^5+\cdots&\\ &=\displaystyle \frac{0}{1}+\frac{0!}{1!}(x-1)-\frac{1!}{2!}(x-1)^2+\frac{2!}{3!}(x-1)^3-\frac{3!}{4!}(x-1)^4+\frac{4!}{5!}(x-1)^5-\cdots&\\ &=\displaystyle (x-1)-\frac{1}{2}(x-1)^2+\frac{1}{3}(x-1)^3-\frac{1}{4}(x-1)^4+\frac{1}{5}(x-1)^5-\cdots&\\ &=\displaystyle \sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}(x-1)^{k}&\\ \end{array} $$

Example: The function $\displaystyle f(x)=\ln x$ can be represented by the power series $\displaystyle \sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}(x-1)^{k}.$

Yeah, but how do we know for what $x$ a series converges?

Absolute Convergence for Series

A series $\displaystyle \sum_{k=0}^{\infty}a_k$ is said to converge absolutely at $x$ if $ \displaystyle \sum_{k=0}^{\infty}\left|a_k\right| $ also converges.

A series $\displaystyle \sum_{k=0}^{\infty}a_k$ is said to converge conditionally at $x$ if $ \displaystyle \sum_{k=0}^{\infty}\left|a_k\right| $ diverges.

The Ratio Test for Series

Let $\displaystyle \sum_{k=1}^{\infty} a_k$ be a series with nonzero terms and let $$L=\lim_{k\rightarrow \infty}\left|\frac{a_{k+1}}{a_k}\right|.$$ If $0 \leq L \lt 1,$ the series converges absolutely.

If $L \gt 1$ or $L=\infty,$ the series diverges.

If $L=1,$ the test is inconclusive.

Absolute Convergence for Power Series

A series $\displaystyle \sum_{k=0}^{\infty}a_k(x-x_0)^k$ is said to converge absolutely at $x$ if $ \displaystyle \sum_{k=0}^{\infty}\left|a_k(x-x_0)^k\right| $ also converges.

A series $\displaystyle \sum_{k=0}^{\infty}a_k(x-x_0)^k$ is said to converge conditionally at $x$ if $ \displaystyle \sum_{k=0}^{\infty}\left|a_k(x-x_0)^k\right| $ diverges.

Ratio Test for Power Series

We may apply the ratio test to the series $\displaystyle \sum_{k=0}^{\infty}a_k(x-x_0)^k.$

The series converges absolutely wherever the inequality $$\displaystyle \lim_{k \rightarrow \infty} \left|\frac{a_{k+1}(x-x_0)^{k+1}}{a_k (x-x_0)^k}\right| \lt 1$$ is satisfied.

Solving this inequality will give us a statement of the form $|x-x_0| \lt \rho.$

The value $\rho$ is the radius of convergence.

Interval of Convergence

To determine the interval of convergence, we need to decide if the endpoints of the interval result in a convergent series. That is, we need to determine if the series converges at one, both, or none of the $x$ values such that $|x-x_0|=\rho.$ (This is the inconclusive case of the Ratio Test.)

The possibilities for the interval of convergence are: $$(x_0-\rho,a+\rho),\,\,\,\, [x_0-\rho,x_0+\rho),\,\,\,\, (x_0-\rho,x_0+\rho],\,\ \mbox{ and }\,\,\,\, [x_0-\rho,x_0+\rho]$$

Example

Determine the radius and interval of convergence of the series representation at $x_0=0$ $$\sin x=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{(2k+1)!}$$

To determine the radius of convergence, $\rho,$ we compute $\displaystyle \lim_{k \rightarrow \infty} \left|\frac{a_{k+1}(x-x_0)^{k+1}}{a_k (x-x_0)^k}\right|.$ $$ \begin{array}{lll} \displaystyle \lim_{k \rightarrow \infty} \left|\frac{a_{k+1}(x-x_0)^{k+1}}{a_k (x-x_0)^k}\right| &=\displaystyle \lim_{k \rightarrow \infty}\left|\frac{\frac{(-1)^{k+1}}{(2(k+1)+1)!}x^{2(k+1)+1}}{\frac{(-1)^k}{(2k+1)!}x^{2k+1}}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|\frac{\frac{(-1)^{k+1}}{(2k+3)!}x^{2k+3}}{\frac{(-1)^k}{(2k+1)!}x^{2k+1}}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|\frac{\frac{(-1)^{k+1}}{(2k+3)!}x^{2}}{\frac{(-1)^k}{(2k+1)!}}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|\frac{(-1)^{k+1}}{(2k+3)!}\cdot \frac{(2k+1)!}{(-1)^k}x^{2}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|-\frac{1}{(2k+2)(2k+3)}x^{2}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|-\frac{1}{(2k+2)(2k+3)}\right|\left|x^{2}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\frac{1}{(2k+2)(2k+3)}x^{2} &\mbox{}\\ &=\displaystyle x^{2}\lim_{k \rightarrow \infty}\frac{1}{(2k+2)(2k+3)} &\mbox{}\\ &=\displaystyle x^2\cdot 0&\mbox{}\\ &\lt \displaystyle 1 &\mbox{}\\ \end{array} $$ Since the above inequality is satisfied for all $x,$ the radius of convergence is $\rho=\infty$ and the series converges absolutely on $(-\infty,\infty).$

The interval of convergence is $(-\infty,\infty).$

Example

Determine the radius and interval of convergence of the series representation at $x_0=1$ $$\ln x=\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^{k+1}}{k}(x-1)^{k}$$

To determine the radius of convergence, $\rho,$ we compute $\displaystyle \lim_{k \rightarrow \infty} \left|\frac{a_{k+1}(x-x_0)^{k+1}}{a_k (x-x_0)^k}\right|.$ $$ \begin{array}{lll} \displaystyle \lim_{k \rightarrow \infty} \left|\frac{a_{k+1}(x-x_0)^{k+1}}{a_k (x-x_0)^k}\right| &=\displaystyle \lim_{k \rightarrow \infty}\left|\frac{\frac{(-1)^{k+1}}{k+1}(x-1)^{k+1}}{\frac{(-1)^{k}}{k}(x-1)^{k}}\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\left|-\frac{k}{k+1}(x-1)\right| &\mbox{}\\ &=\displaystyle \lim_{k \rightarrow \infty}\frac{k}{k+1}\left|x-1\right| &\mbox{}\\ &=\displaystyle \left|x-1\right|\lim_{k \rightarrow \infty}\frac{k}{k+1} &\mbox{}\\ &=\displaystyle \left|x-1\right| &\mbox{}\\ &\lt \displaystyle 1 &\mbox{}\\ \end{array} $$ Thus, the series converges absolutely when $|x-1|\lt 1,$ and the radius of convergence is $\rho=1.$

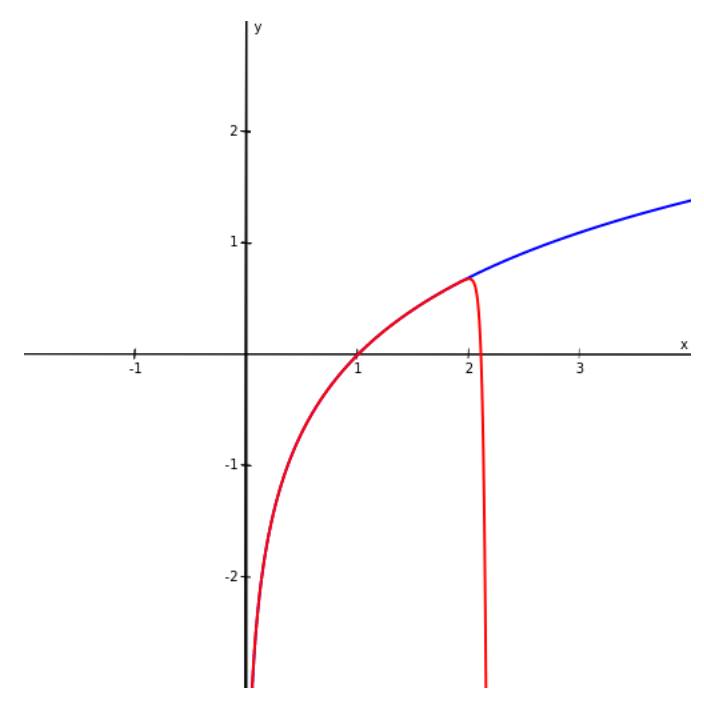
The series converges absolutely on $(0,2).$

Omitting the details, the series diverges at $x=0,$ but converges conditionally at $x=2.$

Therefore, the interval of convergence is $(0,2].$

Other Operations on Power Series

As the above shows, power series can be used to represent functions exactly (under the right conditions, of course) or to give good polynomial approximations of functions.

This alternative way of looking at functions will serve us very well for solving problems wouldn't otherwise be able to solve.

Thus, it will be well worth the effort to understand how we combine power series with other power series to get new power series.

Addition and Subtraction of Power Series

Suppose the power series $\displaystyle \sum_{k=0}^{\infty}a_kx^k$ converges to the function $f(x)$ on an interval $I$ and $\displaystyle \sum_{k=0}^{\infty}b_kx^k$ converges to the function $g(x)$ on the same interval $I.$ Then the following hold:

i.) The power series $\displaystyle \sum_{k=0}^{\infty}a_kx^k \pm \sum_{k=0}^{\infty}b_kx^k=\displaystyle \sum_{k=0}^{\infty}(a_k \pm b_k) x^k$ converges to $f(x) \pm g(x)$ on $I.$
ii.) For any integer $m \geq 0$ and any real number $c,$ the power series $\displaystyle \sum_{k=0}^{\infty}c x^m a_kx^k$ converges to $cx^mf(x)$ for all $x$ in $I.$
iii.) For any integer $m \geq 0$ and any real number $c,$ the power series $\displaystyle \sum_{k=0}^{\infty} a_k(c x^m)^k$ converges to $f(cx^m)$ when $cx^m$ is in $I.$

Examples

Use the series for $\displaystyle \sum_{k=0}^{\infty}x^k=\frac{1}{1-x}$ on $|x| \lt 1$ to construct a series for $\displaystyle \frac{1}{(1-x)(x-2)}.$

Partial fractions again come to the rescue! $$ \begin{array}{lll} \displaystyle \frac{1}{(1-x)(x-2)} &=\displaystyle \frac{A}{1-x}+\frac{B}{x-2} &\mbox{}\\ &=\displaystyle \frac{A(x-2)}{(1-x)(x-2)}+\frac{B(1-x)}{(1-x)(x-2)} &\mbox{}\\ &=\displaystyle \frac{(A-B)x-2A+B}{(1-x)(x-2)} &\mbox{}\\ \end{array} $$ Then $A-B=0$ and $-2A+B=1.$ Solving by inspection, $A=-1$ and $B=-1.$ Thus, $$ \begin{array}{lll} \displaystyle \frac{1}{(1-x)(x-2)} &=\displaystyle -\frac{1}{1-x}-\frac{1}{x-2} &\mbox{}\\ &=\displaystyle -\frac{1}{1-x}+\frac{1}{2-x} &\mbox{}\\ &=\displaystyle \frac{1}{2-x}-\frac{1}{1-x} &\mbox{}\\ &=\displaystyle \frac{1}{2\left(1-\frac{x}{2}\right)}-\frac{1}{1-x} &\mbox{}\\ &=\displaystyle \frac{1}{2}\frac{1}{1-\frac{x}{2}}-\frac{1}{1-x} &\mbox{}\\ &=\displaystyle \frac{1}{2}\sum_{k=0}^{\infty}\left(\frac{x}{2}\right)^k-\sum_{k=0}^{\infty}x^k &\mbox{}\\ &=\displaystyle \frac{1}{2}\sum_{k=0}^{\infty}\frac{x^k}{2^k}-\sum_{k=0}^{\infty}x^k &\mbox{}\\ &=\displaystyle \frac{1}{2}\sum_{k=0}^{\infty}\frac{1}{2^k} x^k-\sum_{k=0}^{\infty}x^k &\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}\frac{1}{2^{k+1}} x^k-\sum_{k=0}^{\infty}x^k &\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}\left(\frac{1}{2^{k+1}} x^k-x^k\right) &\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}\left(\frac{1}{2^{k+1}} -1\right)x^k &\mbox{}\\ \end{array} $$

Find the function represented by the power series $\displaystyle f(x)=\sum_{k=0}^{\infty}\frac{1}{3^k}x^k$ and determine its interval of convergence.

$$ \begin{array}{lll} \displaystyle f(x) &=\displaystyle \sum_{k=0}^{\infty}\frac{1}{3^k}x^k&\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}\frac{x^k}{3^k}&\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}\left(\frac{x}{3}\right)^k&\mbox{}\\ &=\displaystyle \frac{1}{1-\frac{x}{3}}&\mbox{}\\ &=\displaystyle \frac{3}{3-x}&\mbox{}\\ \end{array} $$ Since the interval of convergence for the series $\displaystyle \sum_{k=0}^{\infty}x^k=\frac{1}{1-x}$ is given by $|x|\lt 1,$ the interval of convergence for $f(x)$ is given by $\displaystyle \left|\frac{x}{3}\right|\lt 1.$

Then $$ \begin{array}{llll} &\displaystyle -1 \lt \frac{x}{3} \lt 1&\displaystyle &\mbox{}\\ \implies &\displaystyle -3 \lt x \lt 3 &\displaystyle &\mbox{}\\ \end{array} $$ Thus, the interval of convergence is $(-3,3).$

Multiplying Series

Suppose the power series $\displaystyle \sum_{k=0}^{\infty}a_kx^k$ converges to the function $f(x)$ on an interval $I$ and $\displaystyle \sum_{k=0}^{\infty}b_kx^k$ converges to the function $g(x)$ on the same interval $I$ with $\displaystyle p_k=\sum_{m=0}^{k}a_m b_{k-m}.$

Then the power series $\displaystyle \left(\sum_{k=0}^{\infty}a_kx^k\right)\left(\sum_{k=0}^{\infty}b_kx^k\right) =\sum_{k=0}^{\infty} \left(\sum_{m=0}^{k}a_m b_{k-m}\right)x^k =\sum_{k=0}^{\infty}p_kx^k$ converges to $f(x)\cdot g(x)$ on $I.$

Example

Multiply the power series representation $\displaystyle \frac{1}{1-x}=\sum_{k=0}^{\infty}x^k$ on $|x| \lt 1$ with itself to construct a power series representation of $\displaystyle f(x)=\frac{1}{(1-x)(1-x)}$ on the interval $(-1,1).$

$$ \begin{array}{lll} \displaystyle f(x) &=\displaystyle \frac{1}{(1-x)(1-x)}&\mbox{}\\ &=\displaystyle \frac{1}{1-x}\frac{1}{1-x}&\mbox{}\\ &=\displaystyle \left(\sum_{k=0}^{\infty}x^k\right)\left(\sum_{k=0}^{\infty}x^k\right)&\mbox{}\\ &=\displaystyle \left(\sum_{k=0}^{\infty}a_kx^k\right)\left(\sum_{k=0}^{\infty}b_kx^k\right)&\mbox{}\\ \end{array} $$ where we are letting $a_k=1$ and $b_k=1$ in order to use the above theorem.

Then $$p_k=\sum_{m=0}^{k}a_mb_{k-m}=\sum_{m=0}^{k}1=k+1$$ Thus, $$f(x)=\sum_{k=0}^{\infty}p_kx^k=\sum_{k=0}^{\infty}(k+1)x^k$$

Yeah, but how does this help us solve DEs?

Awesome News!

If we have a power series representation of a function $f(x),$ we want to find a power series representation of its derivative or integral, we simply differentiate or integrate each term in the power series representation of $f(x).$

We shall state this more formally...

Term-by-Term Differentiation and Integration for Power Series

Suppose $f(x)=\displaystyle \sum_{k=0}^{\infty}a_k (x-x_0)^k$ on $(x_0-\rho,x_0+\rho)$ where $\rho \gt 0.$

Then the following hold:

$$f'(x)=\displaystyle \sum_{k=1}^{\infty}a_k k(x-x_0)^{k-1}\,\,\,\,\mbox{on}\,\,\,\,(x_0-\rho,x_0+\rho).$$ $$\displaystyle \int f(x) \, dx=\displaystyle C+ \sum_{k=0}^{\infty}\frac{a_k}{k+1}(x-x_0)^{k+1}\,\,\,\,\mbox{on}\,\,\,\,(x_0-\rho,x_0+\rho).$$

A Nice Fun Example

$$ \begin{array}{lll} \displaystyle \frac{d}{dx}e^{x}&\displaystyle=\frac{d}{dx}\sum_{k=0}^{\infty}\frac{x^{k}}{k!} &\mbox{}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}\frac{kx^{k-1}}{k!} &\mbox{by the above}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}\frac{x^{k-1}}{(k-1)!} &\mbox{}\\ \displaystyle &\displaystyle=\sum_{k=0}^{\infty}\frac{x^{k}}{k!} &\mbox{re-indexing sum}\\ \displaystyle &\displaystyle=e^x &\mbox{}\\ \end{array} $$

Another Nice Fun Example

$$ \begin{array}{lll} \displaystyle \frac{d}{dx}\sin x&\displaystyle=\frac{d}{dx}\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k+1}}{(2k+1)!} &\mbox{}\\ \displaystyle &\displaystyle=\frac{d}{dx}\left(x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\right) &\mbox{}\\ \displaystyle &\displaystyle=1-\frac{3}{3!}x^2+\frac{5}{5!}x^4-\frac{7}{7!}x^6+\cdots &\mbox{by the above}\\ \displaystyle &\displaystyle=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{6}{6!}x^6+\cdots &\mbox{}\\ \displaystyle &\displaystyle=\sum_{k=0}^{\infty}\frac{(-1)^kx^{2k}}{(2k)!} &\mbox{}\\ \displaystyle &\displaystyle=\cos x &\mbox{}\\ \end{array} $$

Another Nice Fun Example

$$ \begin{array}{lll} \displaystyle \frac{1}{(1-x)(1-x)}&\displaystyle= \frac{1}{(1-x)^2} &\mbox{}\\ \displaystyle &\displaystyle=\frac{d}{dx}\frac{1}{1-x} &\mbox{}\\ \displaystyle &\displaystyle=\frac{d}{dx}\left(1+x+x^2+x^3+\cdots\right) &\mbox{}\\ \displaystyle &\displaystyle=1+2x+3x^2+\cdots &\mbox{}\\ \displaystyle &\displaystyle=\sum_{k=0}^{\infty}(k+1)x^k &\mbox{}\\ \end{array} $$ No series multiplication required!

Example

Differentiate the series $\displaystyle \frac{1}{(1-x)^2}=\sum_{k=0}^{\infty}(k+1)x^k=1+2x+3x^2+4x^3+\cdots$ term-by-term to find a power series representation for $\displaystyle \frac{2}{(1-x)^3}$ on the interval $(-1,1).$

$$ \begin{array}{lll} \displaystyle \frac{2}{(1-x)^3} &=\displaystyle \frac{d}{dx} \frac{1}{(1-x)^2}&\mbox{}\\ &=\displaystyle \frac{d}{dx} \sum_{k=0}^{\infty}(k+1)x^k&\mbox{}\\ &=\displaystyle \sum_{k=1}^{\infty}(k+1)kx^{k-1}&\mbox{}\\ &=\displaystyle \sum_{k=0}^{\infty}(k+2)(k+1)x^{k}&\mbox{re-indexing sum}\\ \end{array} $$

Example

Find a power series representation for $f(x)=\ln(1+x)$ by integrating the power series for $f'$ and find its interval of convergence.

We note that $\displaystyle f'(x)=\frac{1}{1+x}=\frac{1}{1-(-x)}$ so that $\displaystyle f'(x)=\sum_{k=0}^{\infty}(-x)^k =\sum_{k=0}^{\infty}(-1)^k x^k.$

Then, $$ \ln(1+x)=f(x)=\int f'(x)\,dx=C+\sum_{k=0}^{\infty}\frac{(-1)^k}{k+1} x^{k+1} $$ Since $f(0)=\ln(1+0)=\ln 1=0,$ we know that $C=0.$ Thus, $$ \ln(1+x)=\sum_{k=0}^{\infty}\frac{(-1)^k}{k+1} x^{k+1} $$ Since the interval of convergence of the above series is the same as that for $\displaystyle f'(x)=\frac{1}{1-(-x)},$ the series converges on $|-x|\lt 1,$ or $(-1,1)$

Checking the endpoints of the the above interval, we see that at $x=1$ we get the alternating harmonic series and at $x=-1$ we get the plain harmonic series.

Thus, the interval of convergence is $(-1,1]$

Example

$$\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^k x^{2k+1}}{2k+1} =x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\cdots$$ is a series representation of a function that you know fairly well.

What function is it?

Let's call our mystery function $f(x).$

Differentiating the above series term by term we have $$f'(x)=\sum_{k=0}^{\infty}(-1)^k x^{2k}=1-x^2+x^4-x^6+x^8-\cdots$$ This series represents the function $f'(x)=\underline{\hspace{4cm}}$ (Any takers?)

$$f'(x)=\sum_{k=0}^{\infty}(-1)^k x^{2k}=\sum_{k=0}^{\infty}(-x^2)^k=\frac{1}{1-(-x^2)}=\frac{1}{1+x^2}$$ What function has $\displaystyle \frac{1}{1+x^2}$ as its derivative?... (Any takers?)

$$\frac{d}{dx}\tan^{-1}x=\frac{1}{1+x^2}$$ Thus, our mystery function is $$f(x)=\tan^{-1}x=\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^k x^{2k+1}}{2k+1} =x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\cdots$$

The above gives us a fun bonus: a series representation for $\displaystyle \frac{\pi}{4}.$ $$\frac{\pi}{4}=\tan^{-1}1=\displaystyle \sum_{k=0}^{\infty}\frac{(-1)^k}{2k+1}$$

$$\displaystyle \pi=\sum_{k=0}^{\infty}\frac{4(-1)^k}{2k+1}$$

Partial Sum $S_N$
	$N$

Historical Sidenote: Srinivasa Ramanujan

Ramanujan discovered the series $${ \frac{1}{\pi}=\frac{2\sqrt{2}}{9801}}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$$ which is still one of the fastest known convergent series for approximating $\pi.$ The first term gets $\pi$ within $6$ decimal places!

$${ \frac{1}{\pi}=\frac{2\sqrt{2}}{9801}}\sum_{k=0}^{\infty}\frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$$

Partial Sum $S_N$
	$N$