We now deal with two situations we have so far been unable handle using the "old" methods:
1) a lot of force is imparted to a system over a very short time, and
2) large forces are applied over small regions of space
A New Kind of "Function"
We seek to make a new function which models a very large force applied over a very short time, or over a very small region of space.
For example, a mass in a mass-system is struck by a hammer.
Another example, a heavy object rests on on a very small area on a beam supported at both ends.
Impulse
Consider a square pulse $\phi(t)=u(t-1)-u(t-2)$ like the one below.
The impulse imparted by this function $\phi(t)$ is the area under the curve. $$ \int_{-\infty}^{\infty}\phi(t)\,dt=\int_{-\infty}^{\infty}u(t-1)-u(t-2)\,dt=\int_1^2\,dt=1 $$
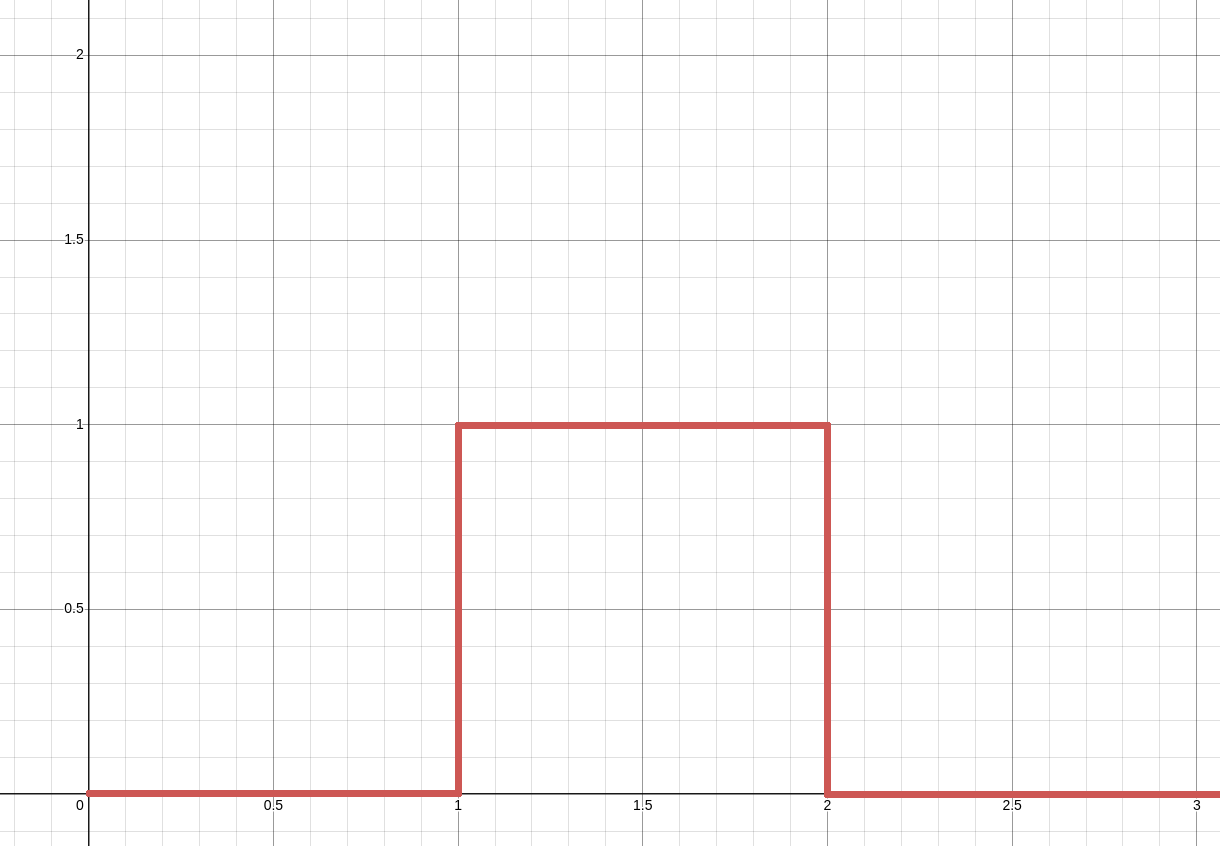
Impulse
If $\phi(t)$ is modelling force, the impulse is merely the change in momentum in the system after $\phi(t)$ is applied to a mass $m$ since by Newton's Second Law, $$ \int_{-\infty}^{\infty}\phi(t)\,dt =\int_{1}^{2}m a(t)\,dt =\int_{1}^{2}m \frac{dv}{dt}\,dt=\int_{1}^{2}m \,dv =m\int_{1}^{2}\,dv =mv(2)-mv(1)=1 $$

Impulse
Suppose we wish to model this change in momentum as if it occurred over a shorter period of time, say over $0.5$ seconds, but without changing the amount of momentum imparted to the system?
What would this function look like?
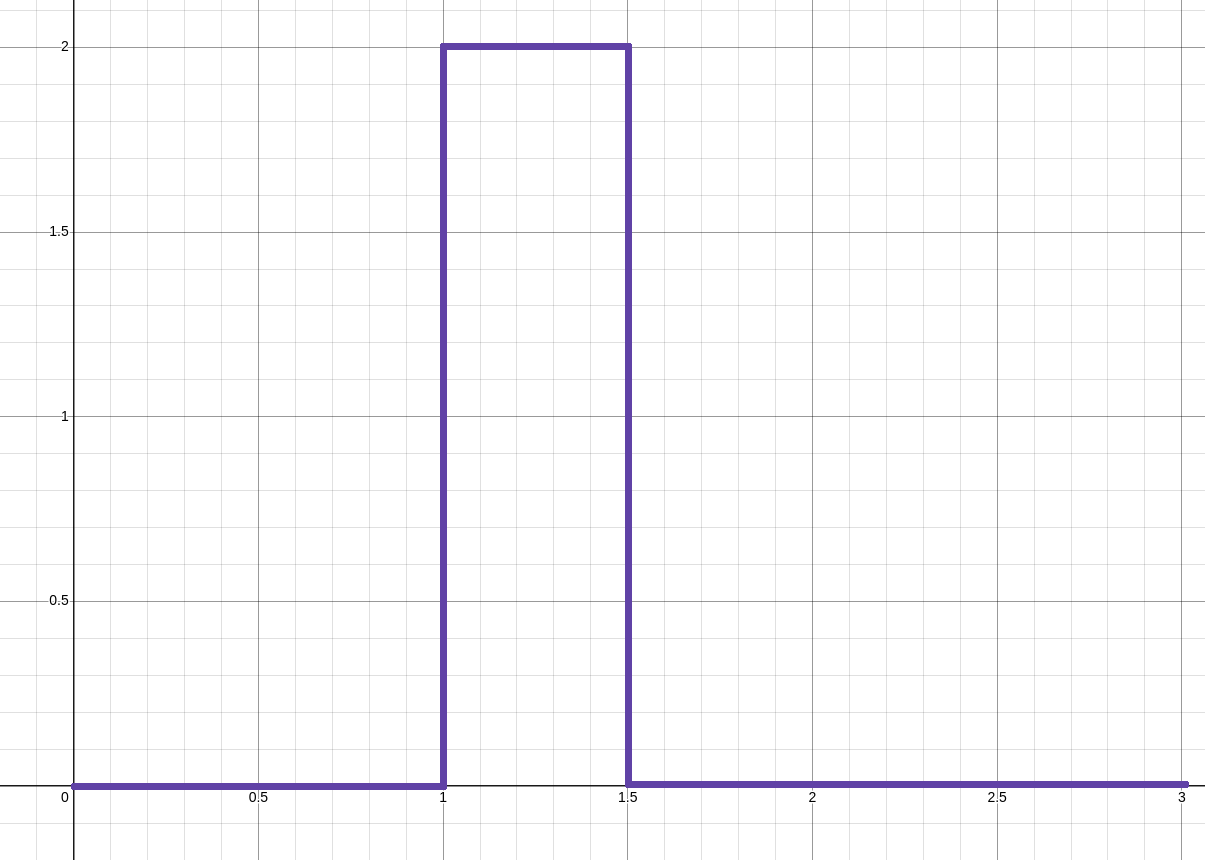
Shrinking the Time Interval
Below is the the same unit change in momentum imparted to the system beginning at $t=1,$ but over shorter and shorter periods of time. $$ \color{#d16460}{\int_{-\infty}^{\infty}\phi(t)\,dt}=\color{#7257b0}{\int_{-\infty}^{\infty}\phi(t)\,dt}=\int_{-\infty}^{\infty}\phi(t)\,dt=\color{#0594f8}{\int_{-\infty}^{\infty}\phi(t)\,dt}=1 $$
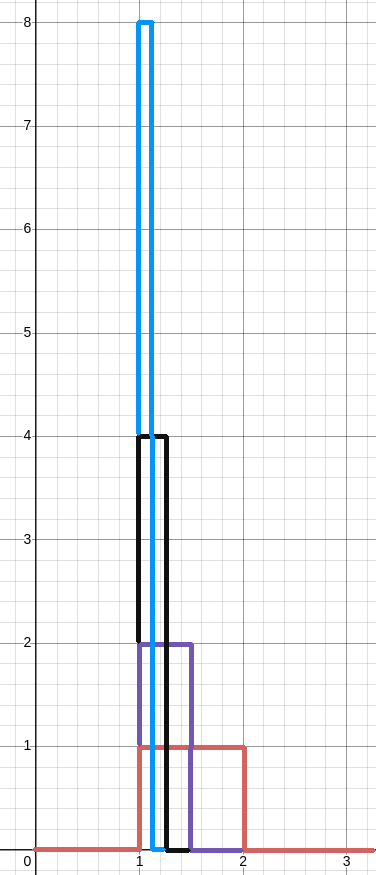
The unit area (impulse, or change in momentum) gets squeezed into an ever thinner, ever taller region.
Shrinking the Time Interval
We could pull these same shenanigans with a pulse that is not square, but curved. The unit area (impulse, or change in momentum) gets squeezed into an ever thinner, ever taller region.
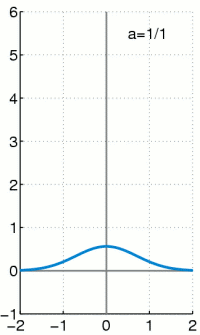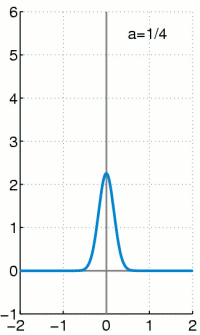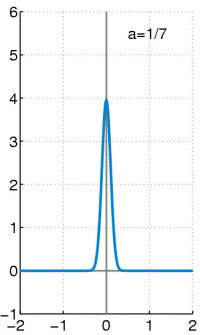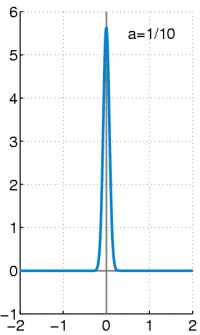
The Dirac Delta Function
The Dirac Delta Function is the limiting "function" of a unit change in momentum as the time interval goes to zero.


The Dirac Delta Function
The Dirac Delta Function $\delta$ is a "function" with the following two properties. $$ \delta(t)=\begin{cases}0 & \mbox{ if }\,\,\,\, t\neq 0\\ \infty & \mbox{ if }\,\,\,\, t= 0\end{cases} $$ $$ \int_{-\infty}^{\infty}\delta(t)\,dt=1 $$ The Dirac Delta function $\delta(t)$ models a very strong instantaneous pulse at time $t=0.$
So, $\delta(t-a)$ models a very strong instantaneous pulse at time $t=a.$
A Property of $\delta(t)$
We may integrate $\delta(t)$ over finite intervals as well with the following properties. $$ \int_{a}^{b}\delta(t)\,dt =\begin{cases}1 & \mbox{ if }\,\,\,\, 0\in[a,b)\\ 0& \mbox{ if }\,\,\,\, 0\not\in [a,b)\end{cases} $$
A Characterizing Property of $\delta$
For any continuous function $f(t),$ $$ \int_{-\infty}^{\infty}\delta(t)f(t)\,dt=f(0) $$ In general, $$ \int_{-\infty}^{\infty}\delta(t-a)f(t)\,dt=f(a) $$
An Observation
Consider the mystery function $\mu$ defined by $$ \mu(t)=\int_{-\infty}^{t}\delta(\tau)\, d\tau $$ What function is this?
$$
\mu(t)=\int_{-\infty}^{t}\delta(\tau)\, d\tau=u(t)
$$
This is the unit step function!
Question: What does this mean??????????????????????
Answer: Very loosely speaking, $\delta(t)=u'(t).$
Question: What does this mean??????????????????????
Answer: Very loosely speaking, $\delta(t)=u'(t).$
Generally (but very loosely) Speaking...
$$ u'(t-a)=\delta(t-a) $$
More About Dirac Delta and the Heaviside Function
For any $a\geq 0,$
$$ \int_{0}^{t}\delta(\tau-a)\, d\tau=u(t-a) $$ $$ \int_{0}^{t}\delta(\tau-a)f(\tau)\, d\tau=u(t-a)f(a) $$
A Public Service Announcement
Please keep in mind we are playing somewhat fast and loose with the standards of mathematical rigor.
That said, this did not stop physicists from using $\delta(t)$ (and with much success!) before mathematicians could figure out the details!
Dirac Delta and Laplace Transforms
The Laplace Transform and the Dirac Delta Function play very nicely with one another.
Laplace Transforms and Dirac Delta
For any $a\geq 0,$ $$ \mathscr{L}\{\delta(t-a)\}=\int_{0}^{\infty}e^{-st}\delta(t-a)\,dt=e^{-as} $$ In particular, $$ \mathscr{L}\{\delta(t)\}=1 $$
We now have everything we need to model instantaneous changes in momentum and masses exerting forces at a point!
Example
Solve the following IVP. $$ x''+x=4\delta(t-1),\,\,\,\,x(0)=1,\,\, x'(0)=0 $$ Note: This equation models a undamped mass-spring system for which momentum is instantaneously (or over a very short period of time) imparted to the system. For example, the mass is struck with a hammer after one second.
$$
\begin{array}{lll}
&\displaystyle x''+x=4\delta(t-1)&\mbox{}\\
\implies &\displaystyle s^2X(s)-sx(0)-x'(0)+X(s)=4e^{-s}&\mbox{}\\
\implies &\displaystyle s^2X(s)-s+X(s)=4e^{-s}&\mbox{}\\
\implies &\displaystyle (s^2+1)X(s)=s+4e^{-s}&\mbox{}\\
\implies &\displaystyle X(s)=\frac{s}{s^2+1}+4e^{-s}\frac{1}{s^2+1}&\mbox{}\\
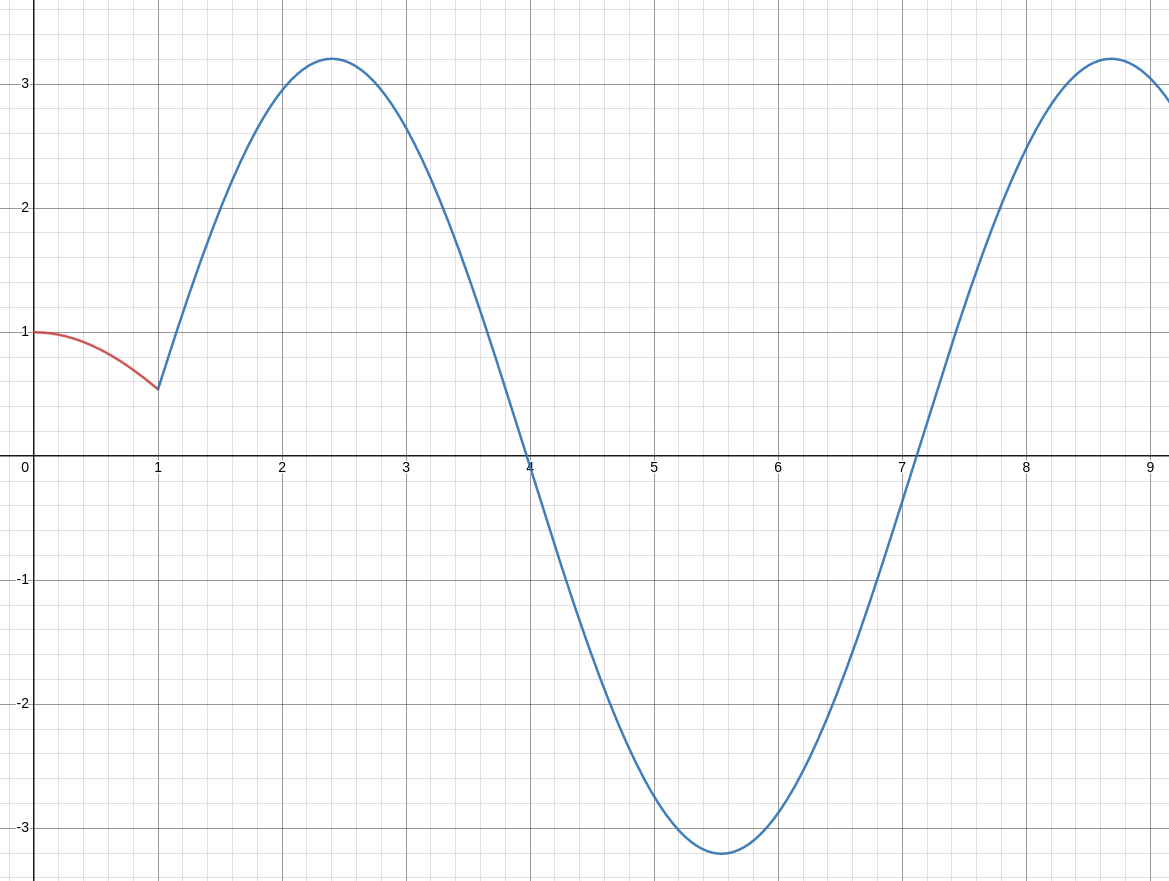
\implies &\displaystyle x(t)=\cos(t)+4u(t-1)\sin(t-1)&\mbox{}\\
\end{array}
$$
The graph of $x(t)$ is given below.

Impulse Response
The above example illustrates how a system is affected by an impulse.
We seek to isolate and understand how this "impulse response" affects a system more generally.
Impulse Response
The solution $x(t)$ to the equation $$ Lx=\delta(t),\,\,\,\,x(0)=0,\,\, x'(0)=0 $$ is called the impulse response of the system.
Recall: Transfer Functions
Transfer functions help us to understand how a system (mass-spring, electrical circuit, etc.) modelled by an equation responds to a forcing function $f(t)$ when all initial conditions set to $0.$
That is to say, we consider an equation $$ Lx=f(t) $$ with initial conditions all zero, and apply the Laplace transform to both sides $$ A(s)X(s)=F(s) $$ We then have $$ X(s)=\frac{1}{A(s)}F(s)=H(s)F(s) $$ The function $H(s)$ is called the transfer function.
Note that $H(s)$ is independent of the input $f(t).$
Impulse Response
Taking the transform of both sides of $$ Lx=\delta(t),\,\,\,\,x(0)=0,\,\, x'(0)=0 $$ we get $$ A(s)X(s)=1 $$ so that $$ X(s)=H(s) $$ In other words, the transform of the impulse response is the transfer function $H(s)!$
Impulse Response
In other words, $h(t)=\mathscr{L}^{-1}\{H(s)\}$ is the impulse response.
Note that some textbooks take the above as the definition of impulse response.
The next result tells us something remarkable about $h(t)...$
Solving $Lx=f(t)$ in General
Consider the IVP $$ Lx=ax''+bx'+cx=f(t),\,\,\,\,x(0)=x_0,\,\,x'(0)=x_1 $$ If $h(t)=\mathscr{L}^{-1}\{H(s)\}$ is the impulse response, then the solution to the IVP is $$ x(t)=x_k(t)+f(t)*h(t) $$ where $x_k$ is the solution to the homogeneous IVP $Lx=0,\,\,\,\,x(0)=x_0,\,\,x'(0)=x_1.$
Dirac Delta and Convolution
Using the equation $$ \int_{0}^{t}\delta(\tau-a)f(\tau)\, d\tau=u(t-a)f(a) $$ we see that $$ \begin{array}{ll} \delta(t-a)*f(t)&\displaystyle=\int_{0}^{t}\delta(\tau-a)f(t-\tau)\, d\tau\\ &=u(t-a)f(t-a)\\ &=\displaystyle\mathscr{L}^{-1}\{e^{-as}F(s)\}\\ \end{array} $$ Of the above equalities, the equation $$ \delta(t-a)*f(t)=u(t-a)f(t-a) $$ will come in handy.
Example
Recall the IVP $$ x''+x=4\delta(t-1),\,\,\,\,x(0)=1,\,\, x'(0)=0 $$ The transfer function is $\displaystyle H(s)=\frac{1}{s^2+1}$ (remember that $H(s)$ is defined for zero initial conditions).
So, the impulse response is $\displaystyle h(t)=\mathscr{L}^{-1}\left\{\frac{1}{s^2+1} \right\}=\sin(t).$ Also, the solution to the homogeneous IVP is $x_k(t)=\cos(t).$ Thus, by the above result, $$ \begin{array}{ll} x(t)&=x_k(t)+f(t)*h(t)\\ %&=x_k(t)+\sin t*4\delta(t-1)\\ &=x_k(t)+4\delta(t-1)*\sin t\\ &=\displaystyle \cos(t)+\int_{0}^{t}4\delta(\tau-1)\sin(t-\tau)\,d\tau\\ &=\cos(t)+4u(t-1)\sin(t-1)\\ \end{array} $$
Example
Solve the IVP for an arbitrary input $f(t).$ $$ x''+x=f(t),\,\,\,\,x(0)=1,\,\, x'(0)=0 $$
$$
\begin{array}{ll}
x(t)&=x_k(t)+f(t)*h(t)\\
&=\cos(t)+f(t)*\sin t\\
&= \displaystyle \cos(t)+\int_{0}^{t}f(\tau)\sin(t-\tau)\,d\tau\\
\end{array}
$$
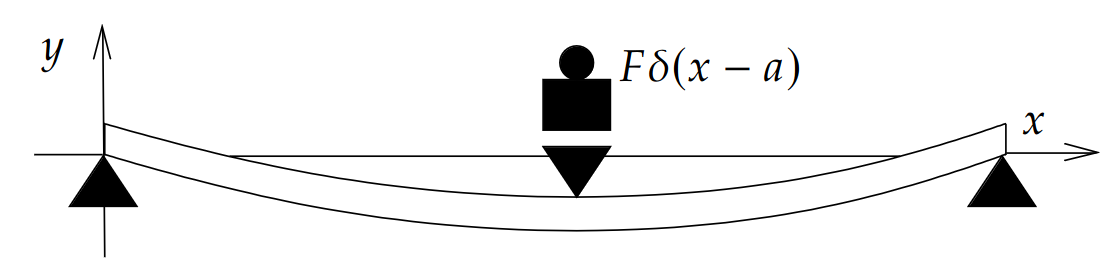
Deflection of a Beam
Suppose we have a steel beam of length $L$ whose ends are resting on two supports.
The deflection $y(x)$ of the beam at $x$ is governed by the Euler-Bernoulli Equation. $$ EI\frac{d^4 y}{dx^4}=F(x) $$ where $F(x)$ is the force applied per unit length, $E$ is the elastic modulus, and $I$ is the second moment of area.
Point Loads
Suppose a force of size $F$ is applied to a steel beam at a point $x=a$ (or over a very small area).
Then the deflection $y(x)$ of the beam at $x$ is governed by $$ EI\frac{d^4 y}{dx^4}=-F\delta(x-a) $$ and the end points satisfy the boundary conditions $$ \begin{array}{lll} \displaystyle y(0)=0&\displaystyle y(L)=0 &\mbox{}\\ \displaystyle y''(0)=0&\displaystyle y''(L)=0 &\mbox{}\\ \end{array} $$ Note that the negative sign in the above equation indicates a downward force.
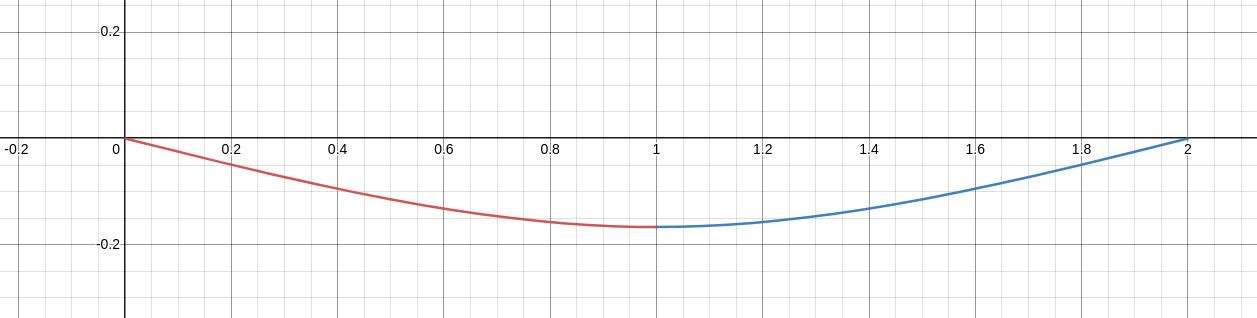
Example: A Point Load
Suppose that length of a steel beam is $2$ with $EI=1.$
Also suppose that a point force $F = 1$ is applied at $x=1.$
State the equation and boundary conditions which describe this situation and solve for the deflection $y(x)$ of the beam.

The equation for the beam deflection is
$$
\frac{d^4 y}{dx^4}=-\delta(x-1)
$$
with boundary conditions
$$
\begin{array}{lll}
\displaystyle y(0)=0&\displaystyle y(2)=0 &\mbox{}\\
\displaystyle y''(0)=0&\displaystyle y''(2)=0 &\mbox{}\\
\end{array}
$$
Taking the transform of both sides of the equation,
$$
\begin{array}{lll}
&\displaystyle \frac{d^4 y}{dx^4}=-\delta(x-1) &\mbox{}\\
\implies &\displaystyle s^4Y(s)-s^3y(0)-s^2y'(0)-sy''(0)-y'''(0)=-e^{-s}&\mbox{using transform table}\\
\implies &\displaystyle s^4Y(s)-s^2y'(0)-y'''(0)=-e^{-s}&\mbox{}\\
\implies &\displaystyle s^4Y(s)-C_1s^2-C_2=-e^{-s}&\mbox{relabelling $y'(0)=C_1$ and $y'''(0)=C_2$}\\
\implies &\displaystyle s^4Y(s)=C_1s^2+C_2-e^{-s}&\mbox{}\\
\implies &\displaystyle Y(s)=\frac{1}{s^4}(C_1s^2+C_2-e^{-s})&\mbox{}\\
\implies &\displaystyle Y(s)=\frac{C_1}{s^2}+\frac{C_2}{s^4}-\frac{e^{-s}}{s^4}&\mbox{}\\
\implies &\displaystyle Y(s)=\frac{C_1}{s^2}+\frac{C_2}{\color{magenta}{6}}\frac{\color{magenta}{6}}{s^4}-\frac{1}{\color{magenta}{6}}e^{-s}\frac{\color{magenta}{6}}{s^4}&\mbox{}\\
\implies &\displaystyle y(x)=C_1x+\frac{C_2}{6}x^3-\frac{1}{6}(x-1)^3u(x-1)&\mbox{applying inverse transform}\\
\end{array}
$$
We may now satisfy the boundary conditions at $x=2.$
$$
\begin{array}{lll}
&\displaystyle y(2)=0 &\mbox{}\\
\implies &\displaystyle C_1\cdot 2+\frac{C_2}{6}(2^3)-\frac{1}{6}(2-1)^3u(2-1)=0&\mbox{}\\
\implies &\displaystyle 2C_1+\frac{4}{3}C_2-\frac{1}{6}=0&\mbox{}\\
\implies &\displaystyle 12C_1+8C_2-1=0&\mbox{}\\
\implies &\displaystyle 12C_1+8C_2=1&\mbox{}\\
\end{array}
$$
And since $y''(x)=C_2x-(x-1)$ for $x \geq 1,$ we have
$$
\begin{array}{lll}
&\displaystyle y''(2)=0&\mbox{}\\
\implies &\displaystyle C_2\cdot 2-(2-1)=0&\mbox{}\\
\implies &\displaystyle 2C_2-1 =0&\mbox{}\\
\implies &\displaystyle C_2 =\frac{1}{2}&\mbox{}\\
\end{array}
$$
From the first equation
$$
\begin{array}{lll}
&\displaystyle 12C_1+8C_2=1&\mbox{}\\
\implies &\displaystyle 12C_1+8\left(\frac{1}{2}\right)=1&\mbox{}\\
\implies &\displaystyle 12C_1+4=1&\mbox{}\\
\implies &\displaystyle C_1=\frac{-3}{12}=-\frac{1}{4}&\mbox{}\\
\end{array}
$$
Our solution is then
$$
\begin{array}{lll}
\displaystyle y(x)&\displaystyle=C_1x+\frac{C_2}{6}x^3-\frac{1}{6}(x-1)^3u(x-1) &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{4}x+\frac{1/2}{6}x^3-\frac{1}{6}(x-1)^3u(x-1) &\mbox{}\\
\displaystyle &\displaystyle=-\frac{1}{4}x+\frac{1}{12}x^3-\frac{1}{6}(x-1)^3u(x-1) &\mbox{}\\
\end{array}
$$

Bonus Example
According to Wikipedia: On 12 April 1831, the [Broughton suspension] bridge collapsed, reportedly due to mechanical resonance induced by troops marching in step. As a result of the incident, the British Army issued an order that troops should "break step" when crossing a bridge.

A simplified model of a large group marching in step over a bridge's resonance frequency is $$ x''+x=\sum_{k=1}^{\infty}\delta(t-2k\pi),\,\,\,\,\, x(0)=0,\,\,\,x'(0)=0. $$ Solve this IVP to understand why armies still observe this practice.
Taking the transform of both sides,
$$
\begin{array}{lll}
&\displaystyle x''+x=\sum_{k=1}^{\infty}\delta(t-2k\pi)&\mbox{}\\
\implies &\displaystyle s^2X(s)+X(s)=\sum_{k=1}^{\infty}e^{-2k\pi}&\mbox{}\\
\implies &\displaystyle X(s)=\sum_{k=1}^{\infty}e^{-2k\pi}\frac{1}{s^2+1}&\mbox{}\\
\implies &\displaystyle x(t)=\sum_{k=1}^{\infty}u(t-2k\pi)\sin(t-2k\pi)&\mbox{}\\
\end{array}
$$
The graph of $x(t)$ is shown below.
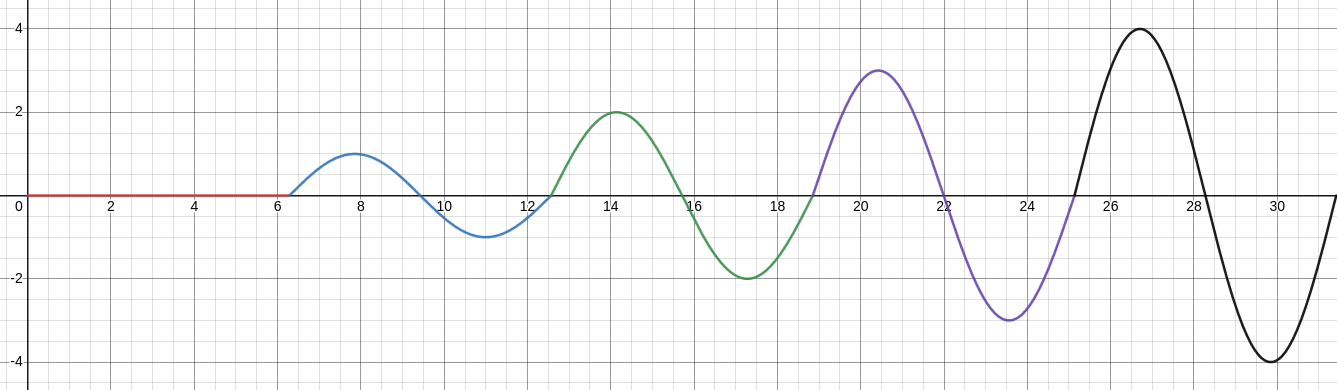
Scenic Alternative
For the system $$ x''+x=\sum_{k=1}^{\infty}\delta(t-2k\pi),\,\,\,\,\, x(0)=0,\,\,\,x'(0)=0. $$ the impulse response function is $h(t)=\sin(t).$
Thus, $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=x_k(t)+f(t)*h(t) &\mbox{}\\ %\displaystyle &\displaystyle=f(t)*h(t) &\mbox{}\\ \displaystyle &\displaystyle=0+\left(\sum_{k=1}^{\infty}\delta(t-2k\pi)\right)*\sin(t) &\mbox{}\\ \displaystyle &\displaystyle=\int_0^t \left(\sum_{k=1}^{\infty}\delta(\tau-2k\pi)\right)\sin(t-\tau)\,d\tau &\mbox{}\\ \displaystyle &\displaystyle=\int_0^t \left(\sum_{k=1}^{\infty}\delta(\tau-2k\pi)\sin(t-\tau)\right)\,d\tau &\mbox{some hand waving}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}\int_0^t \delta(\tau-2k\pi)\sin(t-\tau)\,d\tau &\mbox{more hand waving}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}u(t-2k\pi)\sin(t-2k\pi) &\mbox{}\\ \end{array} $$

Scenic Alternative
For the system $$ x''+x=\sum_{k=1}^{\infty}\delta(t-2k\pi),\,\,\,\,\, x(0)=0,\,\,\,x'(0)=0. $$ the impulse response function is $h(t)=\sin(t).$
Thus, $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=x_k(t)+f(t)*h(t) &\mbox{}\\ %\displaystyle &\displaystyle=f(t)*h(t) &\mbox{}\\ \displaystyle &\displaystyle=0+\left(\sum_{k=1}^{\infty}\delta(t-2k\pi)\right)*\sin(t) &\mbox{}\\ \displaystyle &\displaystyle=\int_0^t \left(\sum_{k=1}^{\infty}\delta(\tau-2k\pi)\right)\sin(t-\tau)\,d\tau &\mbox{}\\ \displaystyle &\displaystyle=\int_0^t \left(\sum_{k=1}^{\infty}\delta(\tau-2k\pi)\sin(t-\tau)\right)\,d\tau &\mbox{some hand waving}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}\int_0^t \delta(\tau-2k\pi)\sin(t-\tau)\,d\tau &\mbox{more hand waving}\\ \displaystyle &\displaystyle=\sum_{k=1}^{\infty}u(t-2k\pi)\sin(t-2k\pi) &\mbox{}\\ \end{array} $$
Our Complete Laplace Transform Table
Table of Laplace Transforms
$$
\begin{array}{cc|cc}
\hline
f(t) & F(s)=\mathscr{L}\{f(t)\} & f(t) & F(s)=\mathscr{L}\{f(t)\}\\ \hline
\displaystyle 1 & \displaystyle \frac{1}{s} & \displaystyle e^{-at}& \displaystyle \frac{1}{s+a} \\ \hline
\displaystyle C & \displaystyle \frac{C}{s} & \displaystyle e^{at}& \displaystyle \frac{1}{s-a} \\ \hline
\displaystyle t & \displaystyle \frac{1}{s^2} & \displaystyle \sin(\omega t) & \displaystyle \frac{\omega}{s^2+\omega^2}\\ \hline
\displaystyle t^2 & \displaystyle \frac{2}{s^3}& \displaystyle \cos(\omega t)& \displaystyle \frac{s}{s^2+\omega^2} \\ \hline
\displaystyle t^3 & \displaystyle \frac{6}{s^4} & \displaystyle \sinh(\omega t) & \displaystyle \frac{\omega}{s^2-\omega^2}\\ \hline
\displaystyle t^n, \,\,\,\,t=1,2,3,\ldots & \displaystyle \frac{n!}{s^{n+1}}& \displaystyle \cosh(\omega t)& \displaystyle \frac{s}{s^2-\omega^2} \\ \hline
\displaystyle t^{r},\,\,\,\,r\gt -1& \displaystyle \frac{\Gamma(r+1)}{s^{r+1}}& \displaystyle u(t-a)& \displaystyle \frac{e^{-as}}{s}\\ \hline
\displaystyle \delta(t) & \displaystyle 1& \displaystyle \delta(t-a)& \displaystyle e^{-as}\\ \hline
\end{array}\\
\Gamma(r)=\int_{0}^{\infty} x^{r-1}e^{-x}\,dx
$$
Properties of the Laplace Transform
$$
\begin{array}{lll}
\hline
&\displaystyle \phi(t) & \Phi(s)=\mathscr{L}\{\phi(t)\}&\\\hline
&\displaystyle e^{-at}f(t)&F(s+a) \\
&\displaystyle f(t-a)u(t-a)& e^{-as}F(s)\\
&f'(t) & sF(s)-f(0)\\
&f''(t) & s^2F(s)-sf(0)-f'(0)\\
&f'''(t) & s^3F(s)-s^2f(0)-sf'(0)-f''(0)\\
&f^{(n)}(t) & s^nF(s)-s^{n-1}f(0)- \cdots -sf^{(n-2)}(t)-f^{(n-1)}(t)\\
&tf(t) & -F'(s)&\\
&t^nf(t) & (-1)^nF^{(n)}(s)&\\
&\displaystyle\frac{1}{t}f(t) & \displaystyle \int_{s}^{\infty}F(\sigma)\,d\sigma\\
&\displaystyle \int_{0}^{t}f(\tau) \,d\tau & \displaystyle \frac{1}{s}F(s) \\
&f(t)*g(t)&F(s)G(s)\\
\hline
\end{array}
$$