With the newly acquired skill of being able to maneuver from the $t$-domain (time) to the $s$-domain (via $\mathscr{L}$) and return safely back again (via $\mathscr{L}^{-1}$) we are now able to solve equations in a new and powerful way.
The Laplace Transform of a Function's Derivative
If $ \mathscr{L}\{f(t)\}=F(s), $ then $$ \mathscr{L}\{f'(t)\}=sF(s)-f(0) $$
$$
\begin{array}{lll}
\displaystyle \mathscr{L}\{f'(t)\}=&\displaystyle=\int_0^{\infty}\underbrace{e^{-st}}_{u}\underbrace{f'(t)}_{v'}\,dt&\mbox{}\\
\displaystyle &\displaystyle=\left[\underbrace{e^{-st}}_{u}\underbrace{f(t)}_{v}\right]_0^{\infty}-\int_0^{\infty}\underbrace{-se^{-st}}_{u'} \underbrace{f(t)}_{v}\,dt &\mbox{by parts}\\
\displaystyle &\displaystyle=\lim_{t\rightarrow \infty}\left[e^{-st}f(t)\right]-\left[e^{-s\cdot 0}f(0)\right]+s\int_0^{\infty}e^{-st}f(t)\,dt &\mbox{}\\
\displaystyle &\displaystyle=0-f(0)+sF(s) &\mbox{}\\
\displaystyle &\displaystyle=sF(s)-f(0) &\mbox{}\\
\end{array}
$$
The Laplace Transform of Higher Derivatives
If $ \mathscr{L}\{f(t)\}=F(s), $ then $$ \begin{array}{ll} \mathscr{L}\{f'(t)\}=sF(s)-f(0)\\ \mathscr{L}\{f''(t)\}=s^2F(s)-sf(0)-f'(0)\\ \mathscr{L}\{f'''(t)\}=s^3F(s)-s^2f(0)-sf'(0)-f''(0)\\ \vdots\\ \mathscr{L}\{f^{(n)}(t)\}=s^nF(s)-s^{n-1}f(0)- \cdots -sf^{(n-2)}(t)-f^{(n-1)}(t)\\ \end{array} $$
We now have everything we need to begin solving initial value problems!
Example
Solve the initial value problem $$ x''+x=\cos(2t),\,\,\,\,x(0)=0,\,\,\,\,x'(0)=1 $$
We may take the Laplace transform of both sides of the equation.
$$
\mathscr{L}\left\{ x''+x \right\}=\mathscr{L}\left\{\cos(2t) \right\}
$$
Then
$$
\begin{array}{lll}
&\displaystyle \mathscr{L}\left\{ x''\right\}+\mathscr{L}\left\{x \right\}=\frac{s}{s^2+4}&\mbox{}\\
\implies &\displaystyle s^2X(s)-sx(0)-x'(0)+X(s)=\frac{s}{s^2+4}&\mbox{}\\
\implies &\displaystyle s^2X(s)-sx(0)-x'(0)+X(s)=\frac{s}{s^2+4}&\mbox{}\\
\implies &\displaystyle s^2X(s)-1+X(s)=\frac{s}{s^2+4}&\mbox{}\\
\implies &\displaystyle (s^2+1)X(s)-1=\frac{s}{s^2+4}&\mbox{}\\
\implies &\displaystyle X(s)=\frac{s}{(s^2+1)(s^2+4)}+\frac{1}{s^2+1}&\mbox{}\\
\end{array}
$$
To find $x(t),$ we must now take the trip back to the time domain via $\mathscr{L}^{-1}.$
To make this easier we will use partial fractions to re-express $\displaystyle \frac{s}{(s^2+1)(s^2+4)}$ in the form $\displaystyle \frac{As+B}{s^2+1}+\frac{Cs+D}{s^2+4}$ since we have non-repeated, irreducible quadratic denominators. $$ \begin{array}{lll} &\displaystyle \frac{As+B}{s^2+1}+\frac{Cs+D}{s^2+4}=\frac{s}{(s^2+1)(s^2+4)}&\mbox{}\\ \implies &\displaystyle \color{magenta}{(s^2+1)(s^2+4)}\frac{As+B}{s^2+1}+\color{magenta}{(s^2+1)(s^2+4)}\frac{Cs+D}{s^2+4}=\color{magenta}{(s^2+1)(s^2+4)}\frac{s}{(s^2+1)(s^2+4)}&\mbox{}\\ \implies &\displaystyle (s^2+4)(As+B)+(s^2+1)(Cs+D)=s&\mbox{}\\ \implies &\displaystyle As^3+Bs^2+4As+4B+Cs^3+Ds^2+Cs+D=s&\mbox{}\\ \implies &\displaystyle (A+C)s^3+(B+D)s^2+(4A+C)s+4B+D=s&\mbox{}\\ \implies &\displaystyle \begin{cases}A&&+C&&=0 \\ &B&&+D&=0 \\ 4A&&+C&&=1 \\ &4B&&+D&=0 \\ \end{cases}&\mbox{}\\ \end{array} $$ By inspection, we see that $B=D=0.$ From there it is not difficult to solve the rest of the system: $\displaystyle A=\frac{1}{3}$ and $\displaystyle C=-\frac{1}{3}.$
Thus, $$ X(s)=\frac{1}{s^2+1}+\frac{s}{(s^2+1)(s^2+4)}=\frac{1}{s^2+1}+\frac{1}{3}\frac{s}{s^2+1}-\frac{1}{3}\frac{s}{s^2+4} $$ We are now set to head back to the time domain. $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s^2+1}+\frac{1}{3}\frac{s}{s^2+1}-\frac{1}{3}\frac{s}{s^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s^2+1}\right\}+\frac{1}{3}\mathscr{L}^{-1}\left\{\frac{s}{s^2+1}\right\}-\frac{1}{3}\mathscr{L}^{-1}\left\{\frac{s}{s^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\sin t+\frac{1}{3}\cos t-\frac{1}{3}\cos (2t) &\mbox{}\\ \end{array} $$
To make this easier we will use partial fractions to re-express $\displaystyle \frac{s}{(s^2+1)(s^2+4)}$ in the form $\displaystyle \frac{As+B}{s^2+1}+\frac{Cs+D}{s^2+4}$ since we have non-repeated, irreducible quadratic denominators. $$ \begin{array}{lll} &\displaystyle \frac{As+B}{s^2+1}+\frac{Cs+D}{s^2+4}=\frac{s}{(s^2+1)(s^2+4)}&\mbox{}\\ \implies &\displaystyle \color{magenta}{(s^2+1)(s^2+4)}\frac{As+B}{s^2+1}+\color{magenta}{(s^2+1)(s^2+4)}\frac{Cs+D}{s^2+4}=\color{magenta}{(s^2+1)(s^2+4)}\frac{s}{(s^2+1)(s^2+4)}&\mbox{}\\ \implies &\displaystyle (s^2+4)(As+B)+(s^2+1)(Cs+D)=s&\mbox{}\\ \implies &\displaystyle As^3+Bs^2+4As+4B+Cs^3+Ds^2+Cs+D=s&\mbox{}\\ \implies &\displaystyle (A+C)s^3+(B+D)s^2+(4A+C)s+4B+D=s&\mbox{}\\ \implies &\displaystyle \begin{cases}A&&+C&&=0 \\ &B&&+D&=0 \\ 4A&&+C&&=1 \\ &4B&&+D&=0 \\ \end{cases}&\mbox{}\\ \end{array} $$ By inspection, we see that $B=D=0.$ From there it is not difficult to solve the rest of the system: $\displaystyle A=\frac{1}{3}$ and $\displaystyle C=-\frac{1}{3}.$
Thus, $$ X(s)=\frac{1}{s^2+1}+\frac{s}{(s^2+1)(s^2+4)}=\frac{1}{s^2+1}+\frac{1}{3}\frac{s}{s^2+1}-\frac{1}{3}\frac{s}{s^2+4} $$ We are now set to head back to the time domain. $$ \begin{array}{lll} \displaystyle x(t)&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s^2+1}+\frac{1}{3}\frac{s}{s^2+1}-\frac{1}{3}\frac{s}{s^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s^2+1}\right\}+\frac{1}{3}\mathscr{L}^{-1}\left\{\frac{s}{s^2+1}\right\}-\frac{1}{3}\mathscr{L}^{-1}\left\{\frac{s}{s^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\sin t+\frac{1}{3}\cos t-\frac{1}{3}\cos (2t) &\mbox{}\\ \end{array} $$
The Big Idea
$$ \begin{array}{ccc} \color{magenta}{\mbox{time domain}}&& \color{blue}{s\mbox{-domain}}\\ \color{magenta}{\mbox{differential equation in } x(t)} & \overset{\Large{\mathscr{L}}}{\LARGE{\longrightarrow}} & \color{blue}{\mbox{algebraic equation in }X(s)}\\ \color{magenta}{calculus}\,\,\,\, \LARGE{\big\downarrow}& & \color{blue}{algebra}\,\,\,\, \LARGE{\big\downarrow} \\ \color{magenta}{\mbox{obtain solution } x(t)} & \underset{\Large{\mathscr{L}^{-1}}}{\LARGE{\longleftarrow}} & \color{blue}{\mbox{algebraic solution }X(s)}\\ \end{array} $$
The Advantages of Solving IVPs with the Laplace Transform
It might seem like the method we just used to solve the above equation is more trouble than it's worth.
Question: Why not just solve the characteristic equation and do a round of undetermined coefficients?
The Advantages of Solving IVPs with the Laplace Transform
Answer: One BIG reason is the Laplace transform can EASILY handle input functions $f(t)$ which are less well-behaved, yet are vitally important to applications.
Examples include functions which model
#1) on/off states in electronics,
#2) limited resources running out (i.e., a rocket running out of fuel)
#3) "pulses" and "point forces"
One example we shall soon see is an input function with jump discontinuities.
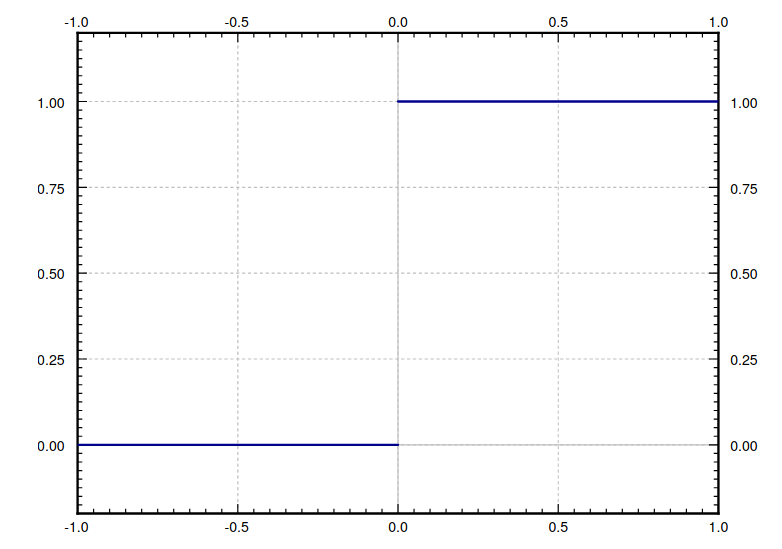
Recall: The Heaviside Function
$$ u(t) =\begin{cases}0 & \mbox{if }\,\,\,\, t\lt 0\\ 1 & \mbox{if }\,\,\,\, t\geq 0\\ \end{cases} $$
Example
Write the function piecewise-defined function $$ f(t)= \begin{cases} 2 & \mbox{if }\,\,\,\, 0\lt t \lt 5\\ 0 & \mbox{if }\,\,\,\, 5\lt t \lt 10\\ e^{4t} & \mbox{if }\,\,\,\, 10\lt t\\ \end{cases} $$ as a combination of unit step functions.
$$
\begin{array}{lll}
\displaystyle f(t)&\displaystyle= [u(t-0)-u(t-5)]\cdot 2+[u(t-5)-u(t-10)]\cdot 0+u(t-10)\cdot e^{4t}&\mbox{}\\
\displaystyle &\displaystyle=2u(t)-2u(t-5)+u(t-10)e^{4t} &\mbox{}\\
\end{array}
$$
Another Nice Property of the Laplace Transform
From a previous example (which is also in our table), we know that $ \displaystyle \mathscr{L}\{ u(t-a) \}=\frac{e^{-as}}{s}. $
The generalization of this is the following useful fact known as the second shifting property. $$ \mathscr{L}\{f(t-a)u(t-a)\}=e^{-as}\mathscr{L}\{f(t)\}=e^{-as}F(s) $$ Another useful way of writing the second shifting property is $$ \mathscr{L}^{-1}\{e^{-as}F(s)\}=f(t-a)u(t-a) $$
Example
Solve the following IVP. $$ x''(t)+x(t)=f(t),\,\,x(0)=0,\,\,x'(0)=0 $$ where $$ f(t)=\begin{cases}1 & \mbox{ if }\,\, 1\leq t \lt 5 \\ 0 & \mbox{ if }\,\, t \lt 1 \mbox{ or } t\geq 5 \end{cases} $$
We first write
$$
f(t)=\begin{cases}1 & \mbox{ if }\,\, 1\leq t \lt 5 \\ 0 & \mbox{ if }\,\, t \lt 1 \mbox{ or } t\geq 5 \end{cases}
$$
as
$$
f(t)=u(t-1)-u(t-5)
$$
We rewrite our IVP as
$$
x''(t)+x(t)=u(t-1)-u(t-5),\,\,x(0)=0,\,\,x'(0)=0
$$
Taking the transform of both sides,
$$
\begin{array}{lll}
&\displaystyle s^2X(s)-sf(0)-f'(0)+X(s)=\frac{e^{-s}}{s}-\frac{e^{-5s}}{s}&\mbox{}\\
\implies &\displaystyle s^2X(s)+X(s)=\frac{e^{-s}}{s}-\frac{e^{-5s}}{s}&\mbox{}\\
\implies &\displaystyle (s^2+1)X(s)=\frac{e^{-s}}{s}-\frac{e^{-5s}}{s}&\mbox{}\\
\implies &\displaystyle X(s)=\frac{e^{-s}}{s(s^2+1)}-\frac{e^{-5s}}{s(s^2+1)}&\mbox{}\\
\implies &\displaystyle X(s)=e^{-s}\frac{1}{s(s^2+1)}-e^{-5s}\frac{1}{s(s^2+1)}&\mbox{}\\
\end{array}
$$
We now use partial fractions to express $\displaystyle \frac{1}{s(s^2+1)}$ as $\displaystyle \frac{A}{s}+\frac{Bs+C}{s^2+1}.$
$$
\begin{array}{lrll}
&\displaystyle \frac{1}{s(s^2+1)}&\displaystyle=\frac{A}{s}+\frac{Bs+C}{s^2+1} &\mbox{}\\
\implies &\displaystyle \frac{1}{s(s^2+1)}\color{magenta}{s(s^2+1)}&\displaystyle=\frac{A}{s}\color{magenta}{s(s^2+1)}+\frac{Bs+C}{s^2+1}\color{magenta}{s(s^2+1)} &\mbox{}\\
\implies &\displaystyle 1&\displaystyle=A(s^2+1)+(Bs+C)s &\mbox{}\\
\implies &\displaystyle 1&\displaystyle=As^2+A+Bs^2+Cs &\mbox{}\\
\implies &\displaystyle 1&\displaystyle=(A+B)s^2+Cs+A &\mbox{}\\
\implies &\displaystyle \begin{cases} A&+B&&=0\\ && C&=0 \\ A&&&=1 \\ \end{cases} &\mbox{}\\
\end{array}
$$
By inspection, $A=1,$ $B=-1,$ and $C=0.$
We then have $$ \frac{1}{s(s^2+1)}=\frac{1}{s}-\frac{s}{s^2+1}. $$ Continuing where we left off, $$ \begin{array}{lll} &\displaystyle X(s)=e^{-s}\frac{1}{s(s^2+1)}-e^{-5s}\frac{1}{s(s^2+1)} &\mbox{}\\ \implies &\displaystyle X(s)=e^{-s}\frac{1}{s(s^2+1)}-e^{-5s}\frac{1}{s(s^2+1)}&\mbox{}\\ \implies &\displaystyle X(s)=e^{-s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)-e^{-5s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)&\mbox{}\\ \implies &\displaystyle x(t)=\mathscr{L}^{-1}\left\{e^{-s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)-e^{-5s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)\right\}&\mbox{}\\ %\implies &\displaystyle x(t)=(1-\cos (t-1))u(t-1)-(1-\cos (t-5))u(t-5)&\mbox{}\\ \end{array} $$ Now, $$ \mathscr{L}^{-1}\left\{\frac{1}{s}-\frac{s}{s^2+1}\right\}=1-\cos t $$ Thus, using the second shifting property, $\mathscr{L}^{-1}\{e^{-as}F(s)\}=f(t-a)u(t-a),$ the solution to our IVP is $$ x(t)=(1-\cos (t-1))u(t-1)-(1-\cos (t-5))u(t-5) $$ The graph of the solution is given below.
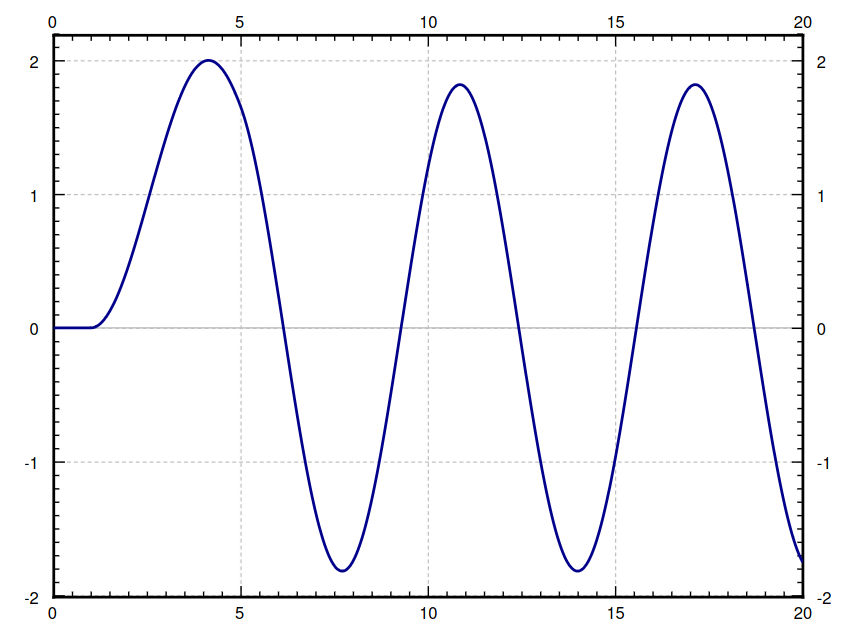
We then have $$ \frac{1}{s(s^2+1)}=\frac{1}{s}-\frac{s}{s^2+1}. $$ Continuing where we left off, $$ \begin{array}{lll} &\displaystyle X(s)=e^{-s}\frac{1}{s(s^2+1)}-e^{-5s}\frac{1}{s(s^2+1)} &\mbox{}\\ \implies &\displaystyle X(s)=e^{-s}\frac{1}{s(s^2+1)}-e^{-5s}\frac{1}{s(s^2+1)}&\mbox{}\\ \implies &\displaystyle X(s)=e^{-s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)-e^{-5s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)&\mbox{}\\ \implies &\displaystyle x(t)=\mathscr{L}^{-1}\left\{e^{-s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)-e^{-5s}\left(\frac{1}{s}-\frac{s}{s^2+1}\right)\right\}&\mbox{}\\ %\implies &\displaystyle x(t)=(1-\cos (t-1))u(t-1)-(1-\cos (t-5))u(t-5)&\mbox{}\\ \end{array} $$ Now, $$ \mathscr{L}^{-1}\left\{\frac{1}{s}-\frac{s}{s^2+1}\right\}=1-\cos t $$ Thus, using the second shifting property, $\mathscr{L}^{-1}\{e^{-as}F(s)\}=f(t-a)u(t-a),$ the solution to our IVP is $$ x(t)=(1-\cos (t-1))u(t-1)-(1-\cos (t-5))u(t-5) $$ The graph of the solution is given below.

Transfer Functions
Transfer functions help us to understand how a system (mass-spring, electrical circuit, etc.) modelled by an equation responds to a forcing function $f(t)$ when all initial conditions set to $0.$
That is to say, we consider an equation $$ Lx=f(t) $$ with initial conditions all zero, and apply the Laplace transform to both sides $$ A(s)X(s)=F(s) $$ We then have $$ X(s)=\frac{1}{A(s)}F(s)=H(s)F(s) $$ The function $H(s)$ is called the transfer function.
Transfer Functions
Consider a system modelled by the IVP $$ x''+ x=f(t), \,\, x(0)=0,\,\, x'(0)=0 $$ Applying the Laplace transform to both sides, $$ s^2X(s)+X(s)=F(s) $$ Solving for $X(s),$ $$ X(s)=\frac{1}{s^2+1}F(s) $$ The transfer function is $\displaystyle H(s)=\frac{1}{s^2+1}.$
Transfer Functions
With the transfer function we can now understand how a system responds to an arbitrary forcing function.
For example, for the above system, if $f(t)=\cos (2t),$ then $$ X(s)=H(s)F(s)=\frac{1}{s^2+1}\frac{s}{s^2+4} $$ We now apply the inverse transform $$ x(t)=\mathscr{L}^{-1}\left\{ \frac{1}{s^2+1}\frac{s}{s^2+4}\right\} =\mathscr{L}^{-1}\left\{\frac{1}{3}\frac{s}{s^2+1}-\frac{1}{3}\frac{s}{s^2+4}\right\} =\frac{1}{3}\cos t-\frac{1}{3}\cos (2t) $$
Example
Find the transfer function $H(s)$ for the IVP $$ y''+2y'+5y=f(t),\,\,\,\,y(0)=0,\,\,y'(0)=0 $$ and use it to solve the equation if $f(t)=1.$
Solving
$$
y''+2y'+5y=f(t),\,\,\,\,y(0)=0,\,\,y'(0)=0
$$
for an arbitrary $f(t),$ we take the transform of both sides.
$$
\begin{array}{lll}
&\displaystyle s^2Y(s)-sy(0)-y'(0)+2(sY(s)-y(0))+5Y(s)=F(s)&\mbox{}\\
\implies &\displaystyle s^2Y(s)+2sY(s)+5Y(s)=F(s) &\mbox{}\\
\implies &\displaystyle (s^2+2s+5)Y(s)=F(s) &\mbox{}\\
\implies &\displaystyle Y(s)=\frac{1}{s^2+2s+5}F(s) &\mbox{}\\
\end{array}
$$
Thus, our transfer function is
$$
H(s)=\frac{1}{s^2+2s+5}
$$
We now solve the IVP for when $f(t)=1.$
For $f(t)=1,$ $\displaystyle F(s)=\frac{1}{s}.$
Then $$ Y(s)=\frac{1}{s^2+2s+5}F(s)=\frac{1}{s^2+2s+5}\frac{1}{s}=\frac{1}{(s^2+2s+5)s} $$ Using partial fractions to express $\displaystyle \frac{1}{(s^2+2s+5)s}$ as $\displaystyle \frac{A}{s}+\frac{Bs+C}{s^2+2s+5},$ $$ \begin{array}{lll} &\displaystyle \frac{1}{(s^2+2s+5)s}=\frac{A}{s}+\frac{Bs+C}{s^2+2s+5} &\mbox{}\\ \implies &\displaystyle \frac{1}{(s^2+2s+5)s}\color{magenta}{(s^2+2s+5)s}=\frac{A}{s}\color{magenta}{(s^2+2s+5)s}+\frac{Bs+C}{s^2+2s+5}\color{magenta}{(s^2+2s+5)s}&\mbox{}\\ \implies &\displaystyle 1=A(s^2+2s+5)+(Bs+C)s&\mbox{}\\ \implies &\displaystyle 1=As^2+2As+5A+Bs^2+Cs&\mbox{}\\ \implies &\displaystyle 1=(A+B)s^2+(2A+C)s+5A&\mbox{}\\ \implies &\displaystyle \begin{cases} A&+B&&=0\\ 2A&& +C&=0 \\ 5A&&&=1 \\ \end{cases} &\mbox{}\\ \end{array} $$ So, $\displaystyle A=\frac{1}{5},$ So, $\displaystyle B=-\frac{1}{5},$ and $\displaystyle C=-\frac{2}{5}.$
Then $$ Y(s)=\frac{1}{(s^2+2s+5)s}=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{s^2+2s+5}-\frac{2}{5}\cdot\frac{1}{s^2+2s+5} $$ Completing the square, $$ \begin{array}{lll} \displaystyle Y(s)&\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{s^2+2s\color{magenta}{+1-1}+5}-\frac{2}{5}\cdot\frac{1}{s^2+2s\color{magenta}{+1-1}+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{s^2+2s+1}-1+5}-\frac{2}{5}\cdot\frac{1}{\color{blue}{s^2+2s+1}-1+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{s^2+2s+1}-1+5}-\frac{2}{5}\cdot\frac{1}{\color{blue}{s^2+2s+1}-1+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{(s+1)^2}+4}-\frac{2}{5}\cdot\frac{1}{\color{blue}{(s+1)^2}+4} &\mbox{}\\ \end{array} $$ From here we would like to use the first shifting property $e^{-as}f(t)=\mathscr{L}^{-1}\{F(s+a)\}$ to find the inverse transform. So, $$ \begin{array}{lll} \displaystyle Y(s)&\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s\color{magenta}{+1-1}}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \left(\frac{s\color{magenta}{+1}}{(s+1)^2+4}-\frac{\color{magenta}{1}}{(s+1)^2+4}\right)-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}+\frac{1}{5}\frac{1}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{5\cdot \color{blue}{2}}\cdot\frac{\color{blue}{2}}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{10}\cdot\frac{2}{(s+1)^2+4} &\mbox{}\\ \end{array} $$ We may now compute the inverse transform. $$ \begin{array}{lll} \displaystyle y(t)&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{10}\cdot\frac{2}{(s+1)^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}-\frac{1}{5}e^{-t}\cos (2t)-\frac{1}{10}e^{-t}\sin(2t) &\mbox{}\\ \end{array} $$
For $f(t)=1,$ $\displaystyle F(s)=\frac{1}{s}.$
Then $$ Y(s)=\frac{1}{s^2+2s+5}F(s)=\frac{1}{s^2+2s+5}\frac{1}{s}=\frac{1}{(s^2+2s+5)s} $$ Using partial fractions to express $\displaystyle \frac{1}{(s^2+2s+5)s}$ as $\displaystyle \frac{A}{s}+\frac{Bs+C}{s^2+2s+5},$ $$ \begin{array}{lll} &\displaystyle \frac{1}{(s^2+2s+5)s}=\frac{A}{s}+\frac{Bs+C}{s^2+2s+5} &\mbox{}\\ \implies &\displaystyle \frac{1}{(s^2+2s+5)s}\color{magenta}{(s^2+2s+5)s}=\frac{A}{s}\color{magenta}{(s^2+2s+5)s}+\frac{Bs+C}{s^2+2s+5}\color{magenta}{(s^2+2s+5)s}&\mbox{}\\ \implies &\displaystyle 1=A(s^2+2s+5)+(Bs+C)s&\mbox{}\\ \implies &\displaystyle 1=As^2+2As+5A+Bs^2+Cs&\mbox{}\\ \implies &\displaystyle 1=(A+B)s^2+(2A+C)s+5A&\mbox{}\\ \implies &\displaystyle \begin{cases} A&+B&&=0\\ 2A&& +C&=0 \\ 5A&&&=1 \\ \end{cases} &\mbox{}\\ \end{array} $$ So, $\displaystyle A=\frac{1}{5},$ So, $\displaystyle B=-\frac{1}{5},$ and $\displaystyle C=-\frac{2}{5}.$
Then $$ Y(s)=\frac{1}{(s^2+2s+5)s}=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{s^2+2s+5}-\frac{2}{5}\cdot\frac{1}{s^2+2s+5} $$ Completing the square, $$ \begin{array}{lll} \displaystyle Y(s)&\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{s^2+2s\color{magenta}{+1-1}+5}-\frac{2}{5}\cdot\frac{1}{s^2+2s\color{magenta}{+1-1}+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{s^2+2s+1}-1+5}-\frac{2}{5}\cdot\frac{1}{\color{blue}{s^2+2s+1}-1+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{s^2+2s+1}-1+5}-\frac{2}{5}\cdot\frac{1}{\color{blue}{s^2+2s+1}-1+5} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{\color{blue}{(s+1)^2}+4}-\frac{2}{5}\cdot\frac{1}{\color{blue}{(s+1)^2}+4} &\mbox{}\\ \end{array} $$ From here we would like to use the first shifting property $e^{-as}f(t)=\mathscr{L}^{-1}\{F(s+a)\}$ to find the inverse transform. So, $$ \begin{array}{lll} \displaystyle Y(s)&\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s\color{magenta}{+1-1}}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \left(\frac{s\color{magenta}{+1}}{(s+1)^2+4}-\frac{\color{magenta}{1}}{(s+1)^2+4}\right)-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}+\frac{1}{5}\frac{1}{(s+1)^2+4}-\frac{2}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{5}\cdot\frac{1}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{5\cdot \color{blue}{2}}\cdot\frac{\color{blue}{2}}{(s+1)^2+4} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{10}\cdot\frac{2}{(s+1)^2+4} &\mbox{}\\ \end{array} $$ We may now compute the inverse transform. $$ \begin{array}{lll} \displaystyle y(t)&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{5}\cdot \frac{1}{s}-\frac{1}{5}\cdot \frac{s+1}{(s+1)^2+4}-\frac{1}{10}\cdot\frac{2}{(s+1)^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}-\frac{1}{5}e^{-t}\cos (2t)-\frac{1}{10}e^{-t}\sin(2t) &\mbox{}\\ \end{array} $$
Transforms of Integrals
Suppose $ \mathscr{L}\{f(t)\}=F(s). $
We've seen that the transform of a derivative results in multiplication of $F(s)$ by $s.$
Question: What do you think the the transform of an antiderivative does?
Transforms of Integrals
If $ \mathscr{L}\{f(t)\}=F(s), $ then $$ \mathscr{L}\left\{ \int_{0}^{t}f(\tau) \,d\tau\right\}=\frac{1}{s}F(s) $$ Equivalently, $$ \mathscr{L}^{-1}\left\{ \frac{1}{s}F(s)\right\}=\int_{0}^{t}f(\tau)\,d\tau $$
Example
Compute $$ \mathscr{L}^{-1}\left\{\frac{1}{s(s^2+1)}\right\} $$
$$
\begin{array}{lll}
\displaystyle \mathscr{L}^{-1}\left\{\frac{1}{s(s^2+1)}\right\}&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s}\frac{1}{s^2+1}\right\} &\mbox{}\\
\displaystyle &\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s}F(s)\right\} &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{t}f(\tau)\,d\tau &\mbox{}\\
\displaystyle &\displaystyle=\int_{0}^{t}\sin \tau \,d\tau &\mbox{}\\
\displaystyle &\displaystyle=-\cos t-(-1)&\mbox{}\\
\displaystyle &\displaystyle=1-\cos t&\mbox{}\\
\end{array}
$$
Example
Recall that for a previous example $$ y''+2y'+5y=1,\,\,\,\,y(0)=0,\,\,y'(0)=0 $$ we had $$ Y(s)=\frac{1}{s}\frac{1}{s^2+2s+5}=\frac{1}{s}\frac{1}{(s+1)^2+4}=\frac{1}{s}\cdot \frac{1}{2}\frac{2}{(s+1)^2+4} $$ The above result makes quick work of the solution. $$ \begin{array}{lll} \displaystyle y(t)&\displaystyle=\mathscr{L}^{-1}\left\{\frac{1}{s}\cdot \frac{1}{2}\frac{2}{(s+1)^2+4}\right\} &\mbox{}\\ \displaystyle &\displaystyle=\int_{0}^{t} \frac{1}{2}e^{-\tau}\sin(2\tau)\,d\tau&\mbox{}\\ \displaystyle &\displaystyle=\frac{1}{5}-\frac{1}{5}e^{-t}\cos (2t)-\frac{1}{10}e^{-t}\sin(2t)&\mbox{}\\ \end{array} $$
Transforms on Calculus Operations
Ignoring the details of initial conditions, we can very roughly summarize how the Laplace transform reduces calculus operations in the time domain to algebraic operations in the $s$-domain. $$ \begin{array}{lll} \color{magenta}{\mbox{time domain}}&&\color{blue}{\mbox{$s$-domain}}\\\hline \color{magenta}{\mbox{derivative}}&\overset{\mathscr{L}}{\longrightarrow} &\color{blue}{\mbox{multiplication by $s$}}\\ \color{magenta}{\mbox{integral}}&\overset{\mathscr{L}}{\longrightarrow}&\color{blue}{\mbox{division by $s$}}\\ \end{array} $$
Big Bonus: Integral Equations
Because the Laplace transform plays so nicely with calculus operations, we get the added bonus we we can also solve integral equations.
Similar to a differential equation, an integral equation is one involving an unknown function and its integral.
Example
Solve the integral equation $$ t^2=\int_{0}^{t}e^{\tau}x(\tau)\,d\tau $$
Taking the transform of both sides,
$$
\begin{array}{lll}
&\displaystyle \frac{2}{s^3}=\frac{1}{s}\mathscr{L}\{e^tx(t)\}&\mbox{}\\
\implies &\displaystyle \frac{2}{s^3}=\frac{1}{s}X(s-1)&\mbox{by first shifting property}\\
\implies &\displaystyle \frac{2}{s^2}=X(s-1)&\mbox{}\\
\implies &\displaystyle \frac{2}{(s+1)^2}=X(s)&\mbox{}\\
\implies &\displaystyle x(t)=\mathscr{L}^{-1}\left\{\frac{2}{(s+1)^2}\right\}&\mbox{}\\
\implies &\displaystyle x(t)=2\mathscr{L}^{-1}\left\{\frac{1}{(s+1)^2}\right\}&\mbox{}\\
\implies &\displaystyle x(t)=2e^{-t}\cdot t&\mbox{using the first shifting property again}\\
\implies &\displaystyle x(t)=2te^{-t}&\mbox{}\\
\end{array}
$$
Question: Do calculus operations in the $s$-domain translate nicely back to the time domain?

Inverse Transforms on Derivatives and Integrals
Suppose $ \mathscr{L}\{f(t)\}=F(s). $
Then $$ \mathscr{L}^{-1}\{F'(s)\}=-tf(t),\,\,\,\,\mbox{or equivalently }\,\,\,\, \mathscr{L}\{tf(t)\}=-F'(s) $$ and $$ \mathscr{L}^{-1}\left\{\int_{s}^{\infty}F(\sigma)\,d\sigma\right\}=\frac{1}{t}f(t),\,\,\,\,\mbox{or equivalently }\,\,\,\, \mathscr{L}\left\{\frac{1}{t}f(t)\right\}=\int_{s}^{\infty}F(\sigma)\,d\sigma $$ One place these come in handy is when solving equations with variable coefficients.
Transforms and Inverse Transforms on Calculus Operations
Ignoring the details of initial conditions, we can very roughly summarize how the Laplace transform and inverse transform reduce calculus operations on one domain to algebraic operations the other. $$ \begin{array}{lll} \color{magenta}{\mbox{time domain}}&&\color{blue}{\mbox{$s$-domain}}\\\hline \color{magenta}{\mbox{derivative}}&\overset{\mathscr{L}}{\longrightarrow} &\color{blue}{\mbox{multiplication by $s$}}\\ \color{magenta}{\mbox{integral}}&\overset{\mathscr{L}}{\longrightarrow}&\color{blue}{\mbox{division by $s$}}\\ \color{magenta}{\mbox{multiplication by $t$}}&\overset{\mathscr{L}^{-1}}{\longleftarrow} &\color{blue}{\mbox{derivative}}\\ \color{magenta}{\mbox{division by $t$}}&\overset{\mathscr{L}^{-1}}{\longleftarrow}&\color{blue}{\mbox{integral}}\\ \end{array} $$
Summary of Properties So Far
Suppose $\mathscr{L}\{f(t)\}=F(s).$ Then $$ \begin{array}{lll} \hline &\displaystyle g(t) & G(s)=\mathscr{L}\{g(t)\}&\\\hline &\displaystyle e^{-at}f(t)&F(s+a) \\ &\displaystyle f(t-a)u(t-a)& e^{-as}F(s)\\ &f'(t) & sF(s)-f(0)\\ &f''(t) & s^2F(s)-sf(0)-f'(0)\\ &f'''(t) & s^3F(s)-s^2f(0)-sf'(0)-f''(0)\\ &f^{(n)}(t) & s^nF(s)-s^{n-1}f(0)- \cdots -sf^{(n-2)}(t)-f^{(n-1)}(t)\\ &tf(t) & -F'(s)&\\ &\displaystyle\frac{1}{t}f(t) & \displaystyle \int_{s}^{\infty}F(\sigma)\,d\sigma\\ &\displaystyle \int_{0}^{t}f(\tau) \,d\tau & \displaystyle \frac{1}{s}F(s) \\ \hline \end{array} $$